Самоанализ педагогической деятельности
Учитель – организатор образовательной деятельности учащихся
Содержание
Проблемы, противоречия в работе учителя математики. Цели и задачи.
Основные черты технологии обучения математики
Организация самостоятельной деятельности учащихся на уроках
Организация работы на уроках математики с применением компьютерных технологий
Организация научно-исследовательской деятельности
Организация внеклассной работы
Методическая работа
Условия профессиональной деятельности
Анализ результативности педагогической деятельности
Выводы
Проблемы, противоречия в работе учителя математики. Цели и задачи
Вот же девятнадцать лет я работаю учителем. Работая всё это время в школе, я поняла, что у некоторых учеников существует недостаточная глубина и осознанность усвоения знаний, низкий уровень самостоятельности, отсутствует заинтересованность в получении новых знаний.
В то же время за последние годы объём учебного материала, который должен усвоить школьник значительно возрос. Информационное общество создало свои проблемы, в частности, проблему информационной перегруженности учащихся и проблему ориентировки в избыточном количестве информации. Ребёнок в этой ситуации будет постоянно неуспешен, потому что он не может выучить всё, что от него требуют! Перегруженные дети просто упускают большую часть информации, которую им не под силу усвоить.
В своей работе, как учителя математики, я выделяю следующие противоречия:
-между необходимостью формирования прочных знаний, умений и навыков и большим объёмом теоретических сведений, получаемых на уроках математики;
- между высокими требованиями, предъявляемыми к математическому образованию школьников и недостаточно сформированными общеучебными умениями и навыками;
- между возрастающей практической значимостью курса математики и дефицитом учебного времени;
Как же быть? Как помочь ребёнку сориентироваться в огромном потоке информации? Общество на самом деле интересует не степень информированности учащегося в различных образовательных областях, а адекватность выпускника школы требованиям сегодняшнего мира.
Для решения данной проблемы, прежде всего, я решила переосмыслить цели и задачи своей профессиональной деятельности, в условиях динамизма и изменчивости окружающего мира.
Я осознала, что моя роль как учителя на современном этапе изменилась - я уже выступаю не как источник знаний, а как организатор образовательной деятельности. Учитель и ученик выступают как партнёры образовательного процесса.
Нужно учитывать, что в современных условиях образование становится непрерывным. Теперь уже невозможно научиться всему раз и навсегда. Учиться можно и нужно всю жизнь, и, собственно, наши предки давно сказали «век живи, век учись», понимая ценность непрерывного образования.
Поэтому, из всего сказанного, передо мной как учителем, встаёт проблема, как научить ребёнка самому находить знания.
В своей работе я отказалась от сложившейся практики построения школьного математического курса, как последовательного изложения готовых результатов и сведений. Я считаю, что «здание» математики должно создаваться на глазах учащихся и с их посильным участием.
Проблема МБОУ «Мухоршибирская средняя общеобразовательная школа №1» – природосообразная и разумно-инновационная педагогика на базе педагогического сотрудничества: равные возможности в соответствии с личным выбором. Исходя из проблемы школы я поставила перед собой следующую цель:
- развивать личность школьника, его творческие способности, интерес к учению, формировать желание и умение учиться.
Для достижения этой цели я решаю следующие задачи:
- обучать планированию отдельных учебных действий и их последовательности;
- создавать такие условия в учебном процессе, чтобы дети учились преодолевать затруднения и умели рассчитывать свои силы;
- приобретали опыт разнообразной деятельности (индивидуальной и коллективной), опыт познания, самопознания, самостоятельности, компетенции.
Ведущей идеей своего опыта считаю создание на уроках условий для успешной, активной и сознательной деятельности учащихся, основанной на использовании рациональных методов и приёмов, постоянно поддерживать интерес к предмету.
В своей работе, как учителя математики, придерживаюсь следующих концепций:
- развитие у учащихся представлений о ведущей роли математики в умственном развитии человека;
- раскрытие внутренней гармонии математики;
- сочетание различных видов деятельности;
- умение создавать у учеников положительную мотивацию, познавательный интерес и творческую атмосферу на уроке.
Руководствуюсь следующими принципами педагогической деятельности:
- организация совместной работы учителя и учащихся, предполагающая планирование, реализацию и оценивание процесса и результата обучения;
- опора на субъективный опыт учащихся, который используется в качестве одного из источников обучения;
- актуализация результатов обучения, предполагающая применение на практике приобретённых знаний, учений и навыков;
- индивидуализация и дифференциация обучения, учёт индивидуальных особенностей, интересов и возможностей класса в целом, групп учащихся и каждого ученика в отдельности;
- развитие образовательных потребностей, предполагающее выявление реальной степени освоения учебного материала учащимися, и определение того минимума, без освоения которого невозможно достижение поставленной цели, построение процесса обучения в целях формирования новых образовательных потребностей.
Всё это вкладывается в рамки моей работы – организация учебной деятельности учащихся.
Основные черты технологии обучения математики
Современная педагогика направлена на развитие личности, т.е. современная школа «это школа развития», где преобладающим характером взаимоотношений являются «субъект-субъектный», основанный на демократизации, диалогичности, открытости. Основными формами организации работы являются групповые и коллективные методы обучения: проблемного изложения, частично-поисковые, исследовательские.
Ведущий тип деятельности учащихся – продуктивный, творческий, проблемный. Учитель в такой ситуации выступает, как организатор образовательного процесса.
Для реализации данных направлений педагогической деятельности я на своих уроках стараюсь применять следующие методы работы.
Метод проектов. Данной технологией я добиваюсь овладение учащимися таких мыслительных операций, как синтез, сравнение, обобщение, индукция, дедукция, абстрагирование. Побуждаю интерес, потребность к получению новых знаний. Происходит развитие навыков коллективной работы, исследовательские навыки.
Пример фрагмента урока алгебры в 8 классе по теме: Теорема Виета
Цели урока: 1) предметные:
а) познавательная – расширение и углубление представлений учащихся о решении квадратных уравнений; организация поисковой деятельности учащихся при формулировке теоремы Виета;
б) практическая – научить применять теорему Виета и обратную ей при решении уравнений;
2) личностные:
развитие умения самостоятельно приобретать новые знания; использование для достижения поставленной задачи уже полученные знания; развитие логического мышления; развитие умения анализировать;
3) коммуникативные:
Воспитание навыков самоконтроля и взаимоконтроля; выработка желания и потребности обобщать полученные факты; развитие самостоятельности и творчества; содействовать побуждению интереса к математике.
II.Актуализация знаний.
Повторение организовать в виде разгадывания кроссворда
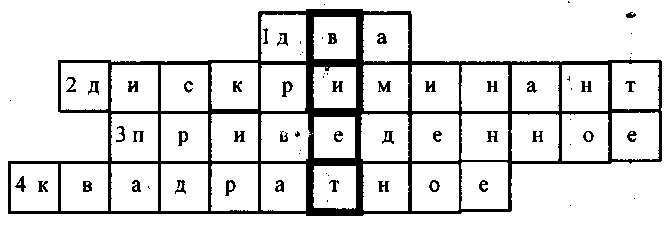
Число корней квадратного уравнения при D0.
Название выражения b2 – 4ac.
Вид квадратного уравнения, в котором а=1.
Уравнение вида ах2+вх+с=0, а≠0 называется…
- Разгадав кроссворд, вы получили фамилию математика Франсуа Виета, жившего в 16 в. и установившего связь между корнями квадратного уравнения и его коэффициентами.
- Итак, тема нашего урока «Теорема Виета».
- Откройте тетради, запишите число и тему урока.
III. Мотивационный этап
- Сейчас мы с вами попытаемся самостоятельно вывести свойства корней квадратного уравнения.
(Для этого я предлагаю классу разбиться на 4 группы и каждой группе даю задание решить квадратные уравнения известными им способами и оформить результаты своей работы в виде таблицы).
Карточка для 1 группы
| Уравнение | а | b | c | b2-4ac | x1 | x2 | x1+x2 | x1·x2 |
| x2+2x-3=0 |
|
|
|
|
|
|
|
|
| x2-4x+3=0 |
|
|
|
|
|
|
|
|
Карточка для 2 группы
| Уравнение | а | b | c | b2-4ac | x1 | x2 | x1+x2 | x1·x2 |
| x2 -4x+3=0 |
|
|
|
|
|
|
|
|
| x2-15x+26=0 |
|
|
|
|
|
|
|
|
Карточка для 3 группы
| Уравнение | а | b | c | b2-4ac | x1 | x2 | x1+x2 | x1·x2 |
| x2+25x+100=0 |
|
|
|
|
|
|
|
|
| x2+5x+4=0 |
|
|
|
|
|
|
|
|
Карточка для 4 группы
| Уравнение | А | b | c | b2-4ac | x1 | x2 | x1+x2 | x1·x2 |
| x2-3x-4=0 |
|
|
|
|
|
|
|
|
| x2-6x-27=0 |
|
|
|
|
|
|
|
|
По результатам проделанной работы ребята из каждой группы высказывают свои предположения. Результатом всей этой проектной деятельности явилась сводная таблица, в которой отразилась зависимость между суммой, произведением корней приведённого квадратного уравнения и его коэффициентами.
| Уравнение | а | b | c | b2-4ac | x1 | x2 | x1+x2 | x1·x2 |
| x2+2x-3=0 | 1 | 2 | -3 | 16 | 1 | -3 | -2 | -3 |
| x2-4x+3=0 | 1 | 5 | -6 | 49 | 1 | -6 | -5 | -6 |
| x2 -4x+3=0 | 1 | -4 | 3 | 4 | 3 | 1 | 4 | 3 |
| x2-15x+26=0 | 1 | -15 | 26 | 121 | 13 | 2 | 15 | 26 |
| x2-3x-4=0 | 1 | 25 | 100 | 225 | -5 | -20 | -25 | 100 |
| x2-6x-27=0 | 1 | 5 | 4 | 9 | -1 | -4 | -5 | 4 |
| x2-3x-4=0 | 1 | -3 | -4 | 25 | 4 | -1 | 3 | -4 |
| x2-6x-27=0 | 1 | -6 | -27 | 144 | 9 | -3 | 6 | -27 |
Ученикам даётся возможность попытаться сформулировать увиденную закономерность о том, что сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равна свободному члену. Данный факт не преподносится учащимся в готовом виде, а предоставляется возможность самостоятельно прийти к математическому открытию.
Далее формулируем теорему Виета и доказываем вместе с учащимся.
Пример фрагмента урока по геометрии в 8 классе по теме «Значение синуса, косинуса, косинуса, тангенса и котангенса для углов 300, 450, 600».
Тип урока: изучение нового материала.
Цели урока:
Предметные:
Создать условия для самостоятельного вывода учащимися значений синуса, косинуса, тангенса и котангенса для углов 300, 450, 600.
Обеспечить закрепление полученных знаний при решении прямоугольных треугольников, используя синус, косинус, тангенс и котангенс острого угла.
Личностные:
Обеспечить развитие самостоятельности при выполнении заданий.
Коммуникативные:
Воспитывать культуру общения в микрогруппе.
Воспитывать умение принимать решения и нести за них ответственность.
Логика процесса усвоения знаний
Актуализация ЗУН, необходимых для вычисления значений синуса, косинуса, тангенса и котангенса для углов 300, 450, 600 (устное решение задач по готовым чертежам).
Задача 1. Найти: 1) sinA, 2) cosA, 3) tgA, 4) ctgA.



13 см
5 см
Изучение нового материала.
Вычисление значение синуса, косинуса, тангенса и котангенса для углов 300, 450, 600 (групповая работа).
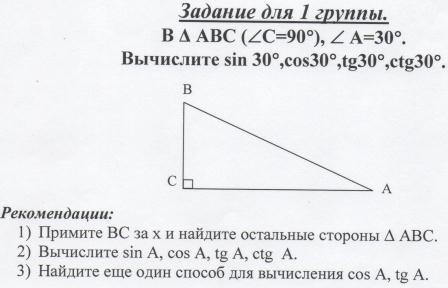


Результаты работы учащиеся заносят в таблицу.
Таблица значений синуса, косинуса, тангенса и котангенса для углов 300, 450, 600.
|
| 300 | 450 | 600 |
| sinα |
|
|
|
| cosα |
|
|
|
| tgα |
|
|
|
| ctgα |
|
|
|
Результаты работы групп заносятся в таблицу слайда с помощью маркера.
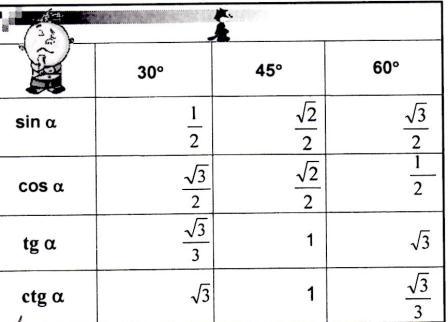
Работа с таблицей (обсуждение способов запоминания таблицы).

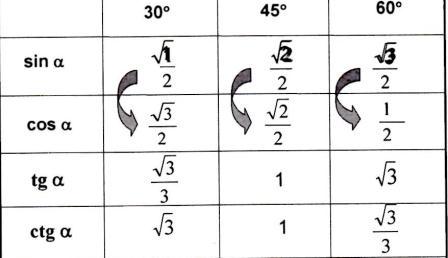
Первичное закрепление изученного материала.
Воспроизведение полученных на уроке табличных знаний. (Заполнение таблицы по памяти и проверка с помощью слайда).
Решение задач на применение табличных значений (групповая работа).
Мини-тестирование по материалам урока (индивидуальная работа за компьютером).
Подведение итогов урока. Выставление оценок за урок. Постановка домашнего задания.
Частично-поисковый метод активизирует познавательную деятельность учащихся по заданному плану. Применяя этот метод на своих уроках, я ставлю перед учащимися проблему и предлагаю алгоритм решения поставленной проблемы.
Фрагмент урока в 6 классе по теме «Длина окружности».
Цели: предметные:
- дать представление о длине окружности;
- установить зависимость между длиной окружности и диаметром;
- ввести число ;
- ознакомить с формулами вычисления длины окружности по известному диаметру или радиусу.
личностные:
- развить внимание, умение обобщать анализировать, делать выводы, обосновывать свои ответы.
коммуникативные:
-аккуратность при оформлении решений;
5. Изучение нового материала.
- Мы повторили, что такое окружность, вспомнили элементы окружности. Давайте вернемся к теме урока «Длина окружности». Длину чего мы умеем измерять? (длину отрезка с помощью линейки)
- А как измерить длину окружности? С помощью какого инструмента?
(выслушиваем предложения учащихся)
- А может быть, и никакого нового инструмента не нужно, и резать ничего не нужно? А может быть существует способ более простой, чтобы найти длину окружности?
Наша сейчас с вами задача найти более простой способ нахождения длины окружности. Для этого нам понадобятся круги и нитки.
Учащимся предлагаю план действий:
Зафиксируем один конец нитки на круге. А затем аккуратно круг «опоясайте» ниткой. Наша нитка образовала окружность, полностью повторяя границу круга.
Растяните нитку, её длина будет приближённо равна длине окружности.
Измерьте длину нитки.
Длину диаметра круга.
Запишите результаты измерений в виде таблицы в тетради.
Найдите отношение длины окружности к длине диаметра.
| Длина окружности С | Длина диаметра d | Отношение C:d |
|
|
|
|
(Учащиеся в таблицу заносят каждый свои результаты измерений, учитель опрашивает несколько учеников и их результаты заносит в заготовленную на доске таблицу)
После проделанной работы учащиеся замечают, что результат вычислений во всех случаях примерно одинаковый. Сравнивают результаты друг с другом. Учитель просит попытаться сформулировать вывод. (выслушиваем суждения ребят, затем учитель подводит итог)
-У вас у всех были разные круги, измерения получились у каждого свои, но вот отношение длины окружности к диаметру этой же окружности у всех примерно получились одинаковые. Небольшую разницу в дробной части числа можно объяснить тем, что в любых измерениях бывают погрешности. Итак, для всех окружностей отношение длины окружности к длине ее диаметра является одно и то же число. Его обозначают буквой .



C:d=
C=d
C=2r
Записи на доске:
Организация самостоятельной деятельности учащихся на уроках
Как я уже говорила выше, объем программного материала возрос, требования к качеству математической подготовки учащихся тоже стал выше и поэтому, чтобы познакомить учащихся с различными приёмами решения задач, я на своих уроках старалась раньше как можно больше решить задач в течение урока. Брала инициативу на себя в ходе решения, сообщая готовые идеи решения заданий. Но однажды я столкнулась с такой проблемой: при самостоятельной работе учащиеся испытывали затруднения в поиске решения заданий, были не уверены в своих действиях. Было и такое, что ученик правильно мыслил, но записать ход решения не мог, не хватало уверенности в своих действиях. Я пришла к выводу, что нужно больше давать возможности учащимся самим искать способы решения, а не преподносить в готовом виде. Большое количество решённых за урок задач, это не всегда качество работы. Поэтому, организовывая работу на уроке, я стараюсь больше предоставлять возможности ученику самому прийти к какому-либо открытию, самому найти способ решения задачи. Эти задачи должны содержать некую практическую или личную значимость для учащегося, чтобы его деятельность в ходе её решения была мотивированной.
Я считаю, что цель решения задачи должна заключаться не столько в получении ответа, сколько в присвоении нового знания (метода, способа решения, приёма), с возможным переносом на другие предметы, т.е. предметное знание должно выступать в роли средства для получения некоего общего межпредметного или общепредметного знания.
С другой стороны, для того, чтобы учебно-познавательная деятельность учащегося стала самостоятельной, должна измениться организация этой деятельности. В этом смысле плодотворным, на мой взгляд, является использование информационных технологий на уроках математики.
Организация работы на уроках математики с применением компьютерных технологий.
Современное обеспечение учебно-воспитательного процесса, а именно компьютеризация, расширяют возможности учителя как организатора образовательного процесса. Персональные компьютеры используются на уроке как средство повышения эффективности учебного процесса.
Необходимость включения информационных технологий в процесс обучения обусловлена несколькими причинами.
Одна из них состоит в том, что применение информационных технологий во всех сферах человеческой жизнедеятельности на сегодняшний день стало необходимым условием успешного функционирования в современном обществе и, значит, должно касаться и школьного образования.
Благодаря комплексу мультимедийных возможностей компьютера работа по созданию уроков с применением новых информационных технологий стала для меня увлекательной.
Использование на уроках мультимедиа приводит к целому ряду положительных эффектов:
- обогащает урок эмоционально;
- психологически облегчает процесс усвоения;
- возбуждает живой интерес к предмету познания;
- возрастает уровень использования наглядности на уроке;
- повышается производительность труда учителя и учащихся на уроке.
Таким образом, все перечисленные факты соответствуют целям образовательного процесса и способствуют лучшему восприятию учащимися учебного материала.
Детям, лучше воспринимающим зрительную информацию, чем звуковую, отображение на экране формулировки определений, теорем, выводов способствует лучшему усвоению.
- Использование мультимедиа в ходе урока способствует не только лучшему усвоению материала урока, но и воспитанию аккуратности при ведении записи в тетради, поскольку учащиеся видят перед собой чёткую, красочно оформленную запись, какую не всегда удаётся сделать на доске с меловыми разводами во время быстрой записи мелом.
На уроках по получению новых знаний в виде лекций презентации служат для иллюстрации объяснения нового материала. При проведении мною уроков в форме беседы слайд-шоу используются для создания проблемной ситуации. В этом случае предъявленные материалы обсуждаются с учащимися, которые в ходе беседы получают навык сравнения и анализа полученной информации, учатся выдвигать гипотезы, искать их подтверждение, правильно интерпретировать увиденное. Использование информационных технологий, работы с интерактивными моделями позволяют активизировать учащихся на занятии, стимулировать их познавательную активность.
При использовании указанного средства обучения могут проявляться и отрицательные качества, если не будут соблюдаться методические требования и условия для достижения эффективного результата.
Значимость использования компьютерных технологий на уроках геометрии обусловлена предметным содержанием. На уроках геометрии, учащиеся много работают с графическим изображением пространственных геометрических фигур, которые не всегда наглядно отражают их свойства. Поэтому особый интерес представляют графические редакторы, позволяющие создавать и изменять компьютерные модели геометрических объектов.
В результате проделанной работы я выделяю следующие преимущества компьютерных моделей пространственных геометрических фигур, по сравнению с традиционными моделями, а также чертежами и рисунками, выполненными на бумаге или доске.
1. Возможность быстрого создания большого количества разнообразных компьютерных моделей геометрических фигур, что затруднено в случае с материальными моделями как в техническом, так и в материальном плане.
2. Неоднократное обращение к компьютерной модели с целью её воспроизведения (демонстрации), в то время как с традиционными моделями действует принцип «здесь и сейчас».
Моментальное копирование компьютерных моделей для индивидуальной работы в классе, что невозможно при работе с материальными моделями и затруднено с чертежами и рисунками.
Возможность динамического изменения количественных характеристик модели объекта, которая полностью исключена в случае с традиционными моделями.
Построение компьютерных моделей может быть реализовано в двумерных и трёхмерных графических редакторах. Очевидно, что при изучении стереометрии используются последние, так как они позволяют создавать компьютерную модель пространственной геометрической фигуры, схожую с её возможной материальной моделью. Это особенно важно и для формирования адекватных пространственных образов изучаемых геометрических фигур.
Организация научно-исследовательской деятельности
Большое внимание в своей работе я уделяю научно-исследовательской деятельности учащихся в рамках деятельности научного общества учащихся (НОУ). Работа в данном направлении развивает творческие способности учащихся. Подготовка докладов позволяет ученику и учителю работать с дополнительными источниками информации, выходить за рамки школьной программы, углублять знания, полученные на уроках. Происходит развитие интереса к предмету. Создаются условия для самореализации учащихся, самоутверждения. Ученики чувствуют себя востребованными. При подготовке к выступлению учащиеся создают презентации. Это требует от них активной переработки материала, выделения главной идеи работы. В процессе создания презентации необходимо переосмыслить имеющуюся информацию, структурировать её, выстроить логическую завершенность каждого слайда. Такая работа приводит учащихся на новый уровень усвоения знаний.
Организация внеклассной работы
Проведение недели точных наук в нашей школе давно уже стало традицией и всегда вызывает у учащихся повышенное внимание и желание поучаствовать в них. Такие мероприятия не только формируют интерес к математике, физике и информатике у самого широкого круга школьников, но и побуждают их к активной творческой деятельности, способствуют развитию навыков общения, сплачивают детский коллектив, делая его настоящей командой. Несомненно, при умелой организации внеклассной работы учитель будет награжден её результатами.
К тому же такая работа повышает квалификацию самого учителя. Ни к одному уроку он не готовиться так много, как к внеклассному мероприятию. Оно позволяет ему остановиться на многих важных и интересных вопросах точных наук, выходящих за пределы учебника или не умещающихся в рамки урока, обратиться к истории математики и т.д.
Проведение недели продумываем на методическом объединении: разрабатываем и расписываем мероприятия по классам с учётом возрастных особенностей. Продумываем оформление мероприятий. Кроме того, сразу после окончания каждого мероприятия подводим итоги, награждаем победителей.
По итогам проведённых внеклассных мероприятий в 2010 году подготовила и выпустила сборник «Неделя математики, информатик и физики». В сборнике были представлены разработки внеклассных мероприятий, проведённых в рамках предметной недели. Отражены итоги проведённых мероприятий и представлен фотоматериал.
Методическая работа
Работая над совершенствованием учебно-воспитательного процесса, большое внимание уделяю методическому росту, самообразованию, мастерству - без чего невозможно добиваться хороших результатов в своей деятельности.
Моя научно-методическая проблема, над которой я работаю уже не первый год - «современные информационные технологии как средство повышения качества обучения». Своим опытом я делюсь с коллегами. Провожу открытые уроки для учителей школы и района, на которых делюсь опытом своей работы.
Активно участвую в работе семинаров, круглых столов, педсоветах.
Условия профессиональной деятельности
Обучение проходит всегда успешнее, если учитель эффективно использует наглядные и технические средства. При этом основная работа проводится в классе, и учитель должен иметь под рукой все необходимое, чтобы обеспечить желаемое разнообразие средств обучения и предъявления информации. В моём кабинете есть учебная литература, наглядные пособия, дидактические материалы, раздаточные материалы дидактического характера, большое количество тестов, цифровые ресурсы. Кабинет должен быть удобен для индивидуальной, групповой, фронтальной работы в любой форме: игровой, исследовательской, творческой, проектной и т.д.
Кабинет №14 Мухоршибирской школы №1. У этого кабинета богатая история: в нём работали Учителя с большой буквы, достигшие больших результатов, имеющие большой авторитет не только в районе, но и в республике: Червинская Нина Ивановна, Покацкая Татьяна Андреевна, Алексеева Галина Фадеевна. И поэтому работать в этом кабинете почётно и ответственно.
Работа с использованием различного дидактического материала позволяет активизировать работу учащихся, увеличивает темп урока, повышает интерес учащихся к предмету, экономит время, что позволяет увеличить объём изучаемого материала, а самое главное обеспечивает творческий процесс обучения и развитие творческой личности.
Работая над изготовлением материала, большое внимание уделяется эстетичному виду, используя возможности компьютера.
Не менее важным является вопрос хранения дидактического материала. Дидактические материалы большей частью разложены по файлам в папках-скоросшивателях. В любой момент можно быстро найти всё необходимое. Тетради для самостоятельных и контрольных работ, обучающихся хранятся в пластиковых боксах для бумаг. Это эстетично и очень удобно. Весь материал размещается и хранится по разделам программы и по классам. Демонстрационные пособия и раздаточный материал хранятся отдельно.
Контрольные и самостоятельные работы в последнее время печатаю не на отдельных листках, а в виде брошюр. Их намного удобнее хранить, использовать на уроках, времени на подготовку к уроку уходит меньше.
В кабинете математики есть доска, имеющая большую рабочую площадь: место нужно и для того, чтобы несколько человек могли одновременно отвечать у доски, и для того, чтобы поместить записи в ходе объяснения нового материала. Для этих целей в кабинете служит и дополнительная доска на задней стене кабинета. Часть основной доски занята координатной сеткой, но она расположена на тыльной стороне, поэтому не привлекает внимания, если не нужна. Створки доски поворачиваются и это удобно, когда ученик готовит на доске решение, которое в нужный момент будет показано классу.
В кабинете почти нет настенных стационарных таблиц с формулами. В последнее время мы требуем знание формул наизусть, т.к. во время экзамена пользоваться справочной литературой запрещено. Постоянно висят только таблица квадратов, таблица простых чисел, таблицы с греческим и латинским алфавитом. Готовые таблицы – сменный материал для урока (формулы сокращенного умножения, изучаемые тригонометрические формулы и т.п.) - появляются по мере необходимости.
На сменных стендах размещена информация для подготовки учащихся к ГИА и ЕГЭ, олимпиадные задания, кроссворды, ребусы, интересные факты из истории математики.
Перед глазами учеников постоянно находятся модели многогранников и фигур вращения, изучаемых по программе и изготовленные учениками. Они способствую развитию пространственного воображения и служат дополнительным визуальным рядом. Этот наглядный материал очень востребован при изучении геометрии, особенно в старших классах.
Портреты математиков являются неотъемлемой частью кабинета, раньше они украшали визуальный ряд задней стены, не отвлекая на себя внимание, и как будто наблюдли за происходящим в кабинете. Но сейчас портреты вывешиваются по мере необходимости. Делая экскурс в историю того или иного фрагмента развития математики, важно познакомить обучающихся с выдающимися математиками. Математика, её история – неотъемлемая часть материальной культуры и истории общества в целом.
В кабинете есть работы учащихся по математике, сообщения на научно-практических конференциях.
Немаловажную роль играют растения. Кабинет математики не должен быть холодным и отталкивающим. В нашем кабинете много цветов, которые повышают влажность и содержание кислорода в помещении.
Анализ результативности педагогической деятельности
Все перечисленные технологии, методы обучения, которые я использую в организации образовательной деятельности, являются результатом:
Модификации (т.е. совершенствования, развития, рационализации) моего прежнего наработанного опыта.
Некоторые заимствованы, но применены в соответствии моему предмету и применены в новых условиях.
Видами моей творческой деятельности являются:
- модификационное творчество;
- комбинированное;
- есть элементы новаторского творчества, в подборе творческих заданий.
Результаты работы можно разделить на следующие группы: учебно-воспитательные, методические, организационные.
Учебно-воспитательные результаты
Повышение качества образовательного процесса, что проявляется:
- в усилении интереса у учащихся, а, следовательно, и повышении мотивации обучения;
- в развитии творческих способностей учащихся;
- в приобретении более глубоких и осмысленных знаний;
- в повышении качества знаний;
- в личном росте учащихся.
Методические результаты:
- создание конкретных методических разработок и использование информационных технологий на уроках;
- проведение и анализ открытых уроков, демонстрирующих использование информационных технологий на уроках математики. И как следствие накопление инновационного опыта по организации и проведению образовательного процесса на новой технологической основе.
Организационные результаты:
- созданы условия для формирования и развития у учащихся информационно-технологической компетенции;
- создании учащимися школы творческих исследовательских работ с использованием информационных технологий;
- в участии учеников в научных конференциях различного уровня.
Выводы
Анализируя опыт своей работы, отслеживая результативность, наблюдая за своими учениками, для себя я сделала следующие выводы, которые являются моим профессиональным кредо, моим «Я» - как учителя, как человека по отношению к учащимся. Чтобы быть Учителем в моём понимании, это значит:
быть с учениками на равных;
создавать на уроках климат творчества, соавторства;
понимать – количество – это не всегда качество;
быть интересным для учащихся, но в тоже время быть загадкой;
давать возможность ученикам делать ошибки и самим их исправлять;
не стоять в стороне от проблем ученика;
быть в постоянном творческом поиске, владеть большим количеством информации.
Каждый учитель начинает работу не на пустом месте. Лекции по педагогике, психологии и методики дают нам общие направления в работе. Кроме того, каждый из нас при обучении в школе видит живой пример своего учителя и на практике следует его опыту, учитывая его достоинства и недостатки. Предметные журналы и газеты щедро дарят нам опыт работы учителей страны. Мне повезло: я начала свою педагогическую деятельность в коллективе математиков, каждый из которых имеет свой почерк работы, и у каждого есть чему поучиться. Но я считаю, что должна создать свой собственный опыт работы. Я не хочу никому подражать, я хочу творчески осмыслить всё, что познаю и практически применяю. Крупицы моих личных удач в преподавании математики, во взаимоотношениях с каждым учеником – это те кирпичики, из которых строится мой опыт работы.
За то время, что я работаю учителем, я поняла, учитель должен быть терпеливым, должен уметь организовать образовательный процесс так, чтобы вовлечь учеников в творческий поиск новых знаний. Наша профессия такова, что каковы бы не были успехи, на достигнутом останавливаться нельзя, и надо продолжать совершенствование методов обучения в своей работе.
Я училась в сельской школе и работаю в ней же. На селе все хорошо знают друг друга, много родственников и близких знакомых. Всех родителей своих учеников я знаю хорошо, знаю обстановку в каждой семье, знаю состояние здоровья каждого ученика. Всё это и помогает мне в работе и усложняет: раз знаю, то всё моё поведение должно соответствовать знанию в каждом конкретном случае. Это трудно осуществить, но стремиться нужно.



























