Самостоятельная работа по теме "Геометрический смысл производной"

1вариант

1)Прямая у = 4х +13 параллельна касательной к графику функции у = х² – 3х + 5. Найдите абсциссу точки касания.

2) Прямая у = 2х +37 является касательной к графику функции у = х³ +3х² – 7х + 10. Найдите абсциссу точки касания.

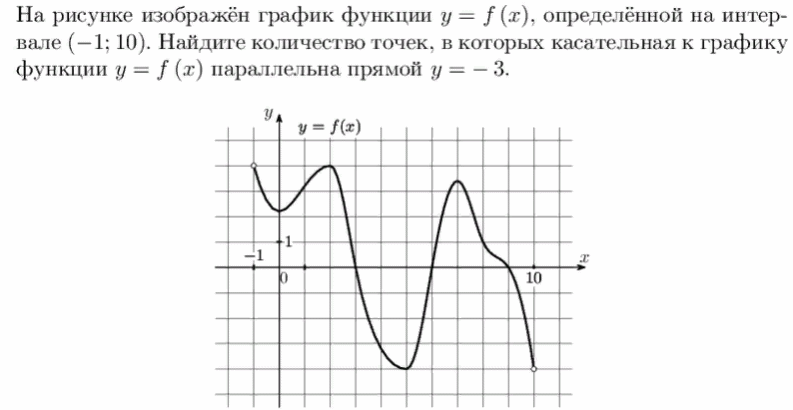
3)На рисунке изображен график функции у = f(х), определенной на интервале ( - 1; 10). Найдите количество точек, в которых касательная параллельна прямой у = − 3

4) На рисунке изображены график функции у = (х) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции f(х) в точке х₀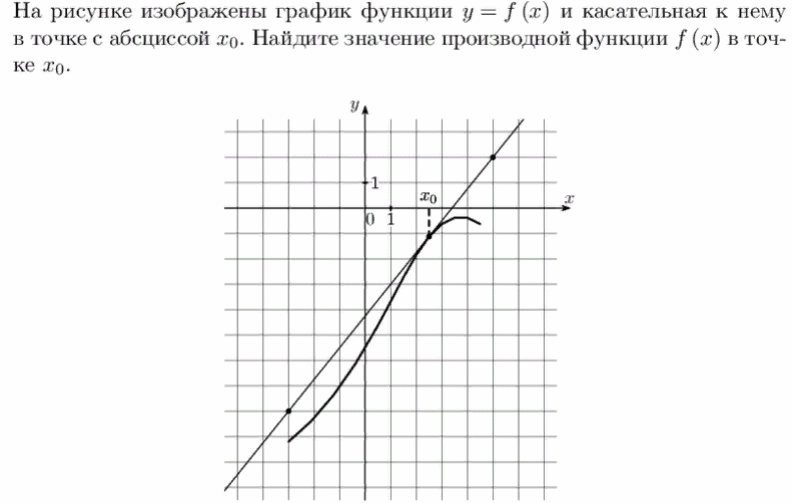

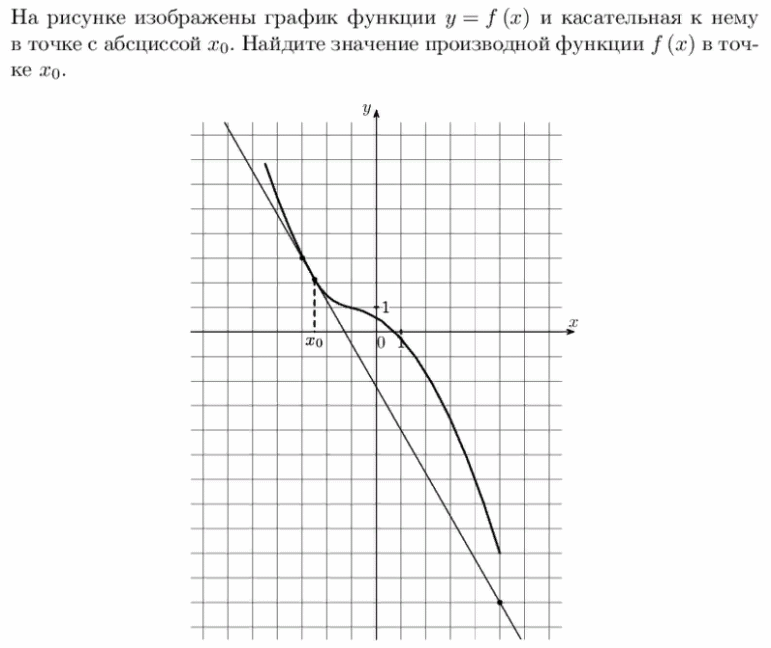
5) На рисунке изображены график функции у = (х) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции f(х) в точке х₀

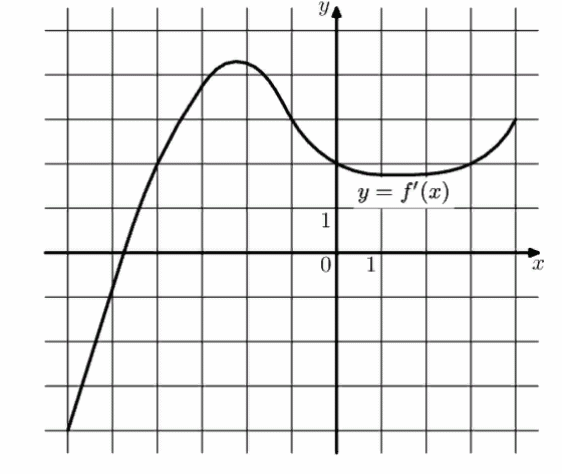
6) На рисунке изображен график у = f'(х) – производной функции f(х). Найдите абсциссу точки , в которой касательная к графику функции у = f(х) параллельна прямой у = 8 – 5 х или совпадает с ней.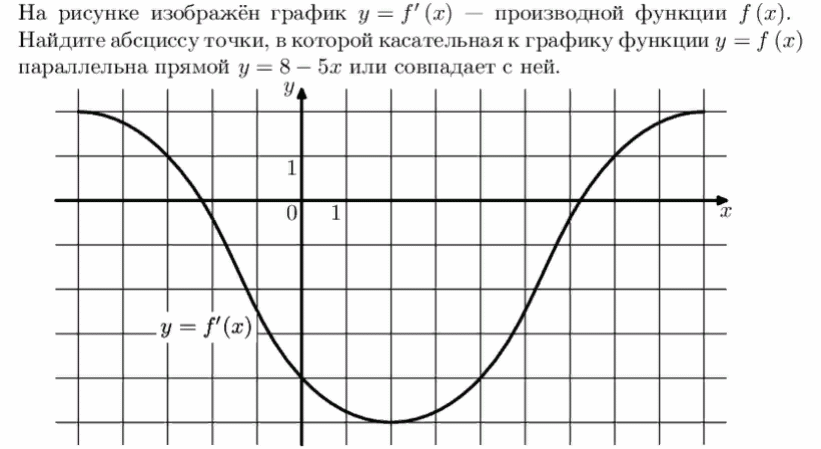

2 вариант.

1)Прямая у = 6х +9 параллельна касательной к графику функции у = х² + 7х − 6. Найдите абсциссу точки касания.

2) Прямая у = −2х −12 является касательной к графику функции у = х³ −2х² – 6х −4. Найдите абсциссу точки касания.

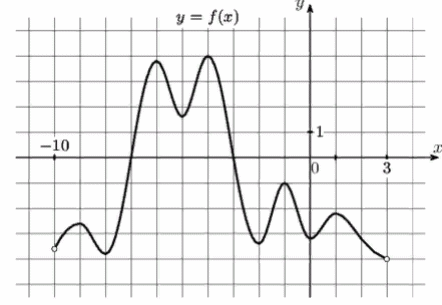
3)На рисунке изображен график функции у = f(х), определенной на интервале ( - 10; 3). Найдите количество точек, в которых касательная параллельна прямой у = − 3

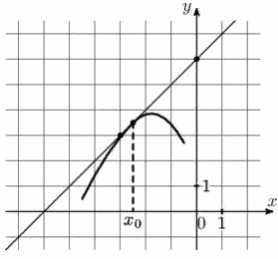
4) На рисунке изображены график функции у = (х) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции f(х) в точке х₀.

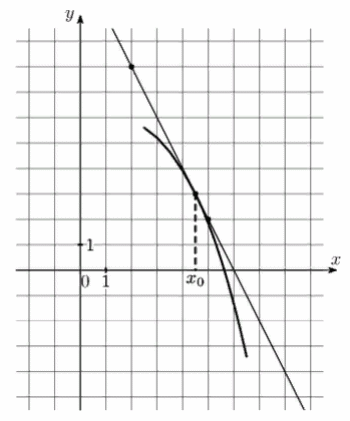
5) На рисунке изображены график функции у = (х) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции f(х) в точке х₀

6) На рисунке изображен график у = f'(х) – производной функции f(х). Найдите абсциссу точки , в которой касательная к графику функции у = f(х) параллельна прямой у = 8 – 5 х или совпадает с ней.

3 вариант.

1)Прямая у = 6х +8 параллельна касательной к графику функции у = х² −3х +5. Найдите абсциссу точки касания.

2) Прямая у = 8х −9 является касательной к графику функции у = х³ +х² + 8х − 9. Найдите абсциссу точки касания.

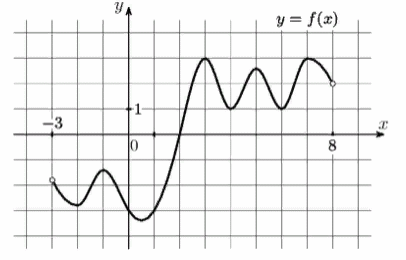
3)На рисунке изображен график функции у = f(х), определенной на интервале ( - 3; 8). Найдите количество точек, в которых касательная параллельна прямой у = − 20

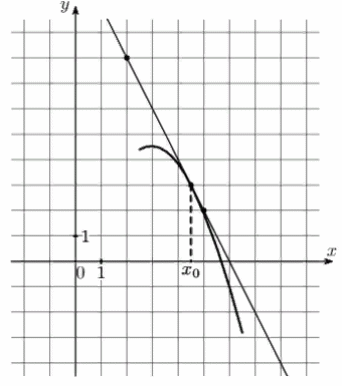
4) На рисунке изображены график функции у = (х) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции f(х) в точке х₀.

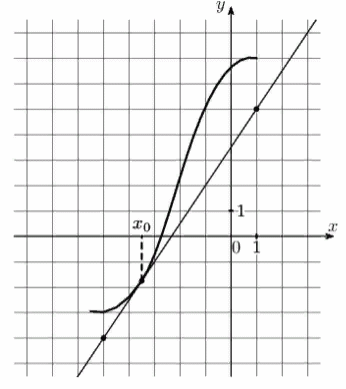
5) На рисунке изображены график функции у = (х) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции f(х) в точке х₀

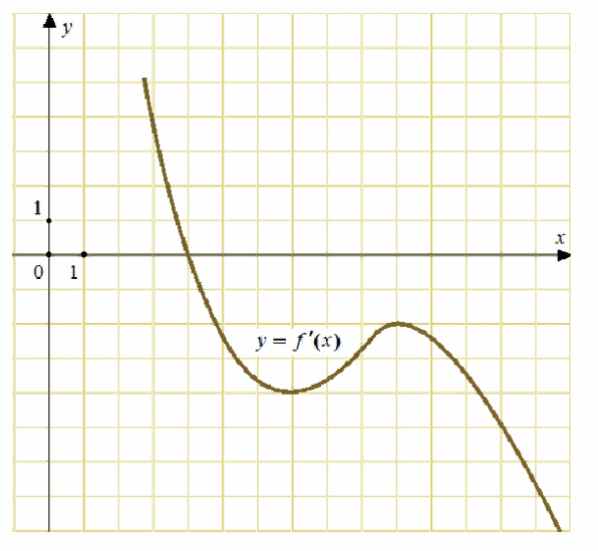
6) На рисунке изображен график у = f'(х) – производной функции f(х). Найдите абсциссу точки , в которой касательная к графику функции у = f(х) параллельна прямой у = 3 х - 6 или совпадает с ней.

4 вариант.

1)Прямая у =−5х −6 параллельна касательной к графику функции у = х² +8х −7. Найдите абсциссу точки касания.

2) Прямая у = −х + 4 является касательной к графику функции у = х³ +х² − х + 4. Найдите абсциссу точки касания.

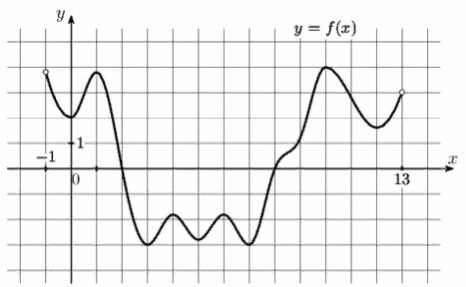
3)На рисунке изображен график функции у = f(х), определенной на интервале ( - 1; 13). Найдите количество точек, в которых касательная параллельна прямой у = 20

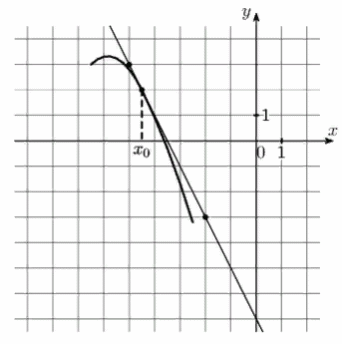
4) На рисунке изображены график функции у = (х) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции f(х) в точке х₀.

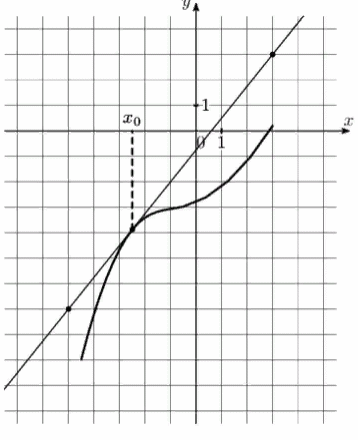
5) На рисунке изображены график функции у = (х) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции f(х) в точке х₀

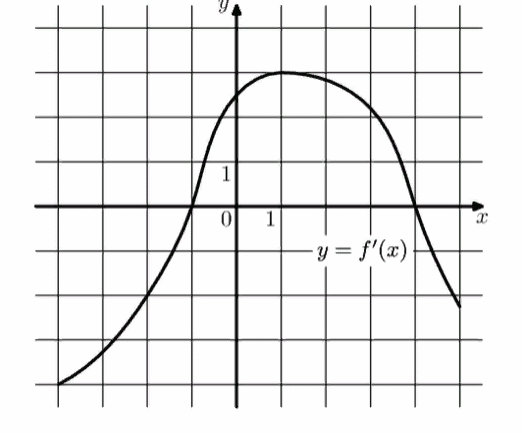
6) На рисунке изображен график у = f'(х) – производной функции f(х). Найдите абсциссу точки , в которой касательная к графику функции у = f(х) параллельна прямой у = 8 − х или совпадает с ней.