Просмотр содержимого документа
«Самостоятельная работа по теме "Квадратичная функция" 9 класс»
Вариант 1
На рисунке изображены графики функций вида y = ax2 + c. Установите соответствие между графиками и знаками коэффициентов a и c.
ГРАФИКИ
1. Найдите координаты вершины параболы: у = -2x2 + 5x + 3.
2. Постройте график функции у = х2 + 3х - 4.
Найдите по графику:
а) значение у при х = -1;
б) значения х, при которых у = -4; Исследуйте свойства функций.
3. Используя шаблон параболы у = х2, постройте в одной системе координат графики функций:
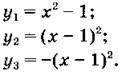
Вариант 2
0. На рисунке изображён график функции вида y = ax2 +bx+c. Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. 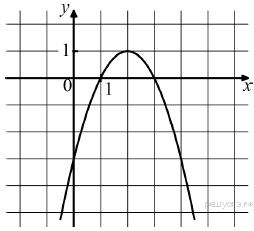
| УТВЕРЖДЕНИЯ | | ПРОМЕЖУТКИ |
| А) функция возрастает на промежутке Б) функция убывает на промежутке | | 1) [0; 3] 2) [−1; 1] 3) [2; 4] 4) [1; 4] |
1. Найдите координаты вершины параболы: у = 3х2 - 4х - 7.
2. Постройте график функции у = -х2 - 3х + 4.
Найдите по графику:
а) значение у при х = -1;
б) значения х, при которых у = 4; Исследуйте свойства функций.
3. Используя шаблон параболы у = х2, постройте в одной системе координат графики функций:
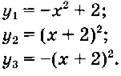
Вариант 3
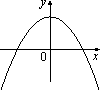
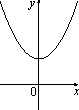
Установите соответствие между функциями и графиками. A) 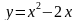 ; Б)
; Б) 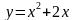 ; В)
; В) 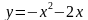
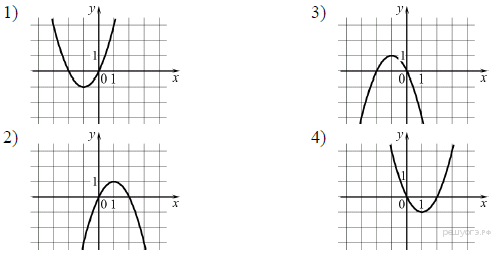
1. Найдите координаты вершины параболы: у = -3x2 + 6x + 3.
2. Постройте график функции у =2х2 -4х +6.
Н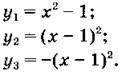 айдите по графику:
айдите по графику:
а) значение у при х = -1;
б) значения х, при которых у = -2; Исследуйте свойства функций.
3. Используя шаблон параболы у = х2, постройте в одной системе координат графики функций:
Вариант 4
0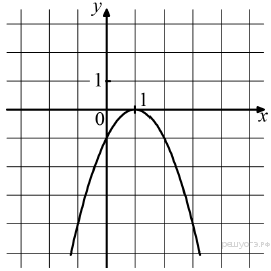 . На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются
. На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются
| УТВЕРЖДЕНИЯ | | ПРОМЕЖУТКИ |
| А) функция возрастает на промежутке Б) функция убывает на промежутке | | 1) [1;2] 2) [0;2] 3) [-1;0] 4) [-2;3] |
1. Найдите координаты вершины параболы: у = 3х2 - 4х - 7.
2. Постройте график функции у = -х2 - 3х + 4.
Н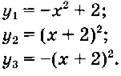 айдите по графику:
айдите по графику:
а) значение у при х = -1;
б) значения х, при которых у = 4; Исследуйте свойства функций.
3. Используя шаблон параболы у = х2, постройте в одной системе координат графики функций:







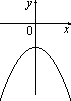
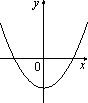
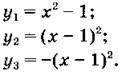

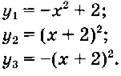
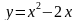 ; Б)
; Б) 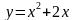 ; В)
; В) 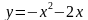
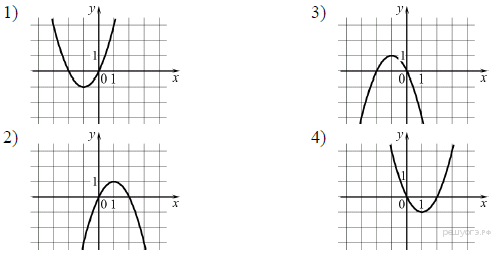
 . На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются
. На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются









