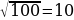| II. Оперативдүү-когнитивдик этап. 1) Пифагор теоремасынын ачылышы. Изилдөө иш-аракеттери. (Жуп болуп иштөө) Маселени чыгаруу : Окуучулардан жупташып кичи топтордо иштөөсүн сураңыз.Алдын ала чакмак кагаз барактарын даярдап коюңуз, бир чакмак бир квадраттык сантиметрге барабар экенин билдириңиз.(4-5 мүн.) Берилген фигуралардын аянтын тапкыла жана эки кичинесинин аянттарынын суммасын чоңунун аянтын салыштыргыла. .(чакмактын жагы 1см), бул кандай фигура Бул фигуралардан тик бурчтуу үч бурчтукту түзгүлө. а=8 , b=6 c=10 S=a*a=8*8=64, S=b*b=6*6=36 S=c*c=10*10=100 64+36=100    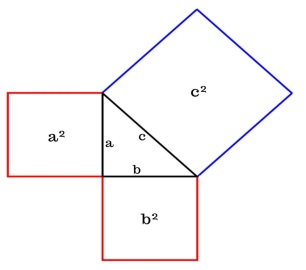
Окуучуларга фигуралардын аянтын табууга жана тик бурчтуу үч бурчтукту түзүүгө жардам берүү үчүн өзүңүздүн кадамдарыңызды атап жана иш-аракетиңизди көрсөтүңүз Фигуралардын жактарынын жардамы аркылуу аянтын табуунун формуласын пайдаланабыз .Формула кандай эле? Чоң фигуранын аянтын кичине фигуралардын аянттарынын суммасы менен салыштырабыз Ушул фигуралардан тик бурчтуу үч бурчтукту түзүп, баракка жармаштыргыла.
Мугалимге кеңеш: Окуучуларда карандаш, сызгыч,калың чакмак кагаздан жасалган фигуралар бар болушун көзөмөлдөө керек.(чакмактын жагы 1см)
Талкулоо:бир нече окуучудан жооптору менен бөлүшүүсүн жана ар бири өздөрүнүн ой жүгүртүү жолун түшүндүрүп берүүсүн сураныңыз.
-Силер кандай жоопту алдыңар? -Силер кантип фигуралардын жактары аркылуу фигура түздүңөр? -Фигуралардын аянттарын кантип тапканыңарды түшүндүрүп бере аласыңарбы? -Маселенин чыгарылышынын башка ыкмасы менен ким бөлүшө алат? Карама-каршы пикир жаратуу: Окуучуга башка паралель класстын окуучусунун жообу төмөндөгүдөй болду.Эки кичине квадраттын аянтынын суммасы чоң квадраттын аянтынан чоң болот. Р=8*4=32 Р=6*4=24 Р=10*4=40 32+24  40 40 Ал фигураларды түзүп, аянтын эмес бардык жактарын кошуу менен периметрин таап, эки кичине фигураны чоң фигура менен салыштырган. Окуучудан сураңыз: Силер аны менен макулсуңарбы же макул эмессиңерби? Эмне үчун ушундай жооп алды? Бул окуучуга анын жообу туура эмес экенин кантип түшүндүрөт элеңер? Окуучунун тапшырмасын доскага илинет, талкууланат Моделдештирүү жана жыйынтыктоо: Жыйынтыктаңыз, маселе кандай чыгарылгандыгына көңүл буруңуз. 1-далилдөө жолу 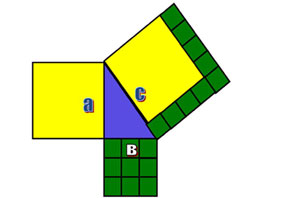
Тик бурчтуу үч бурчтуктун биринчи катетине жактарынын узундугу 4 бирдик квадратка барабар болгон квадрат түзөбүз, экинчи катетине да жактарынын узундугу 3 бирдик квадратка барабар болгон квадрат тургузабыз жана гипотенузага да анын узундугуна барабар квадрат түзөбүз. Жактары а га барабар болгон квадраттын аянтын S1 = а2 =4*4=16 Жактары в га барабар болгон квадраттын аянтын S2 = b 2 =3*3=9 Жактары с га барабар болгон квадраттын аянтын S3 = с 2 =5*5=25 S3= S1+ S2=16+9=25 демек c² = a² + b².
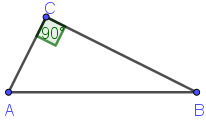
2-далилдөө жолу 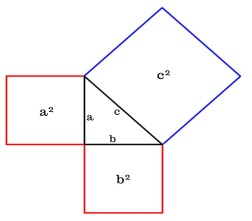 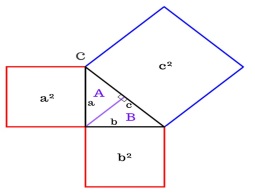 Бул сүрөттө с- гипотенуза, а жана b –катеттер.Үч бурчтуктун тик бурчунан гипотенузага перпендикуляр түз сызык жүргүзөбүз. Ошентип баштапкы чоң С тик бурчтуу үч бурчтугунун ичинде А жана В эки жаңы тик бурчтуу үч бурчтуктары пайда болду. Баштапкы үч бурчтуктун (С)аянты эки жаңы кичинелердин суммасына барабар. С = А + B “Пифагор шымын” 3 окшош фигурага бөлөбүз. 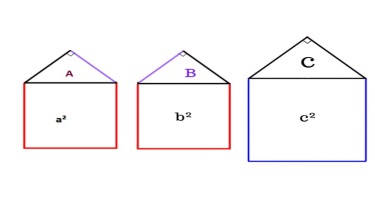 Бардык 3 үч бурчтук бири-бирине окшош жана ушундан улам "үй фигуралары" да окшош. Демек А жана а2 аянтынын катышы B жана b 2, C жана с 2 аянтынын катышы менен бир дей катышат. Башкача айтканда 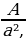 = = 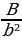 = = 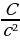 = β катышты грек тамгасы менен белгилейбиз β . = β катышты грек тамгасы менен белгилейбиз β . Квадраттардын ар биринин аянты аркылуу ар бир үч бурчтуктун аянты төмөнкүгө барабар A = βa², B = βb², C = βc²; Бул формула эсибизде С = А + B, т. е. βc² = βa² + βb², c² = a² + b².   3-далилдөө жолу (Евклиддин далилдөөсү) 3-далилдөө жолу (Евклиддин далилдөөсү)

с 2= а2+ b 2 Катеттерге тургузулган квадраттар 2 барабар үч бурчтуктан турат.Ал эми гипотенуза түзүлгөн квадрат ушундай 4 үч бурчтуктан турат.Пифагор теоремасы биринчи жолу тең капталдуу тик бурчтуу үч бурчтук үчүн берилген. С (гипотенузага түзүлгөн квадраттын аянты а жана b (катеттерге) түзүлгөн квадраттардын аянттарынын суммасына барабар. Демек , Пифагордун теоремасы- тик бурчтуу үч бурчтуктун гипотенузасынын квадраты катеттердин квадраттарынын суммасына барабар. с 2= а2+ b 2 Пифагордун теоремасын күнүмдүк жашоодо колдонуу Силерге суроо Пифагордун теоремасы бизди курчап турган чөйрөдө кантип жана каерде колдонууга болот? Силер кандай ойлойсуңар? Ой-жүгүртөлү... Пифагордун теоремасын күнүмдүк турмушта жер тилкесинин периметрин, аянтын табууда, спортто биатлонисттер,өрт өчүрүүдө, аянтын табууда, курулушта, астрономияда, мобилдик байланышта (слайд) Практикалык иш : ( сүрөтүн тартып,) Жогорку деңгээл: R=200 км радиуста байланыш кабыл алынышы үчүн мобилдик оператордун антеннасынын максималдуу бийиктиги канча болуш керек.(жердин радиусу 6380 км ге барабар) Чыгарылышы:    В АВ=х, ВС= R=200 км ОС=r В АВ=х, ВС= R=200 км ОС=r
 АХА С ОВ=ОА+АВ ОВ=r+ х АХА С ОВ=ОА+АВ ОВ=r+ х
    Туура келген деңгээл: Үйдүн бийиктиги 3 м. Андан 8 м аралыкта бийиктиги 9 м болгон мамы(столба) бар.Мамыдан үйгө зым тартылган.Зымдын узундугун тапкыла. Чыгарылышы: Туура келген деңгээл: Үйдүн бийиктиги 3 м. Андан 8 м аралыкта бийиктиги 9 м болгон мамы(столба) бар.Мамыдан үйгө зым тартылган.Зымдын узундугун тапкыла. Чыгарылышы:
  B B
  9 м E C 9 м E C
 3 м A D 3 м A D
 8 м 8 м
Чыгарылышы: BC2= CE2+ ЕB2 BC2 =82 + (9-3)2 BC2=64+36 BC=10  Төмөнүрөөк деңгээл Төмөнүрөөк деңгээл

Мышыктын баласы даракка тыгылып калган. Чыркырап жардам сурады, ооба , бул жерде маселе : өрт өчүрүүчү өз тепкичтерин даракка 6 метрден жакындата албайт. Дарактын бийиктиги 8 метрди түзөт. Өрт өчүргүч тепкичти 11 метрден ашык эмес керип алат. Сиз мышыктын баласын сактап калуу үчүн ушулар жетиштүү деп ойлойсузбу?
 с 2= а2+ b 2= 82+ 6 2=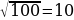 Туура келген деңгээл: №2-көнүгүү Погорелов
| 1-вариант | Катет а | Катет в | Гипотенуза с | | 1 | 3 | 4 | с= | | 2 | 1 | 1 | с = | | 3 | 5 | 6 | с = |
“Бир эле учурда тейбл раунду" - бул түзүм, анда командада 4 катышуучу бир убакта өз алдынча иш аткарат жана убакыт бүткөндөн кийин текшерүү үчүн бири-бирине тегерек боюнча өткөрүп берет. Эталон боюнча текшерүү. - Дептерлерди алмаштыруу. - Слайдды карап, чечимди текшерип, баа бериңиз.
| 










 40
40



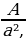 =
= 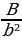 =
= 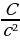 = β катышты грек тамгасы менен белгилейбиз β .
= β катышты грек тамгасы менен белгилейбиз β .
 3-далилдөө жолу (Евклиддин далилдөөсү)
3-далилдөө жолу (Евклиддин далилдөөсү)









 В АВ=х, ВС= R=200 км ОС=r
В АВ=х, ВС= R=200 км ОС=r АХА С ОВ=ОА+АВ ОВ=r+ х
АХА С ОВ=ОА+АВ ОВ=r+ х

 Туура келген деңгээл: Үйдүн бийиктиги 3 м. Андан 8 м аралыкта бийиктиги 9 м болгон мамы(столба) бар.Мамыдан үйгө зым тартылган.Зымдын узундугун тапкыла. Чыгарылышы:
Туура келген деңгээл: Үйдүн бийиктиги 3 м. Андан 8 м аралыкта бийиктиги 9 м болгон мамы(столба) бар.Мамыдан үйгө зым тартылган.Зымдын узундугун тапкыла. Чыгарылышы:
 B
B
 9 м E C
9 м E C 3 м A D
3 м A D 8 м
8 м Төмөнүрөөк деңгээл
Төмөнүрөөк деңгээл