1 723
35 436 
© 2023, id27655497 14982 431
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 07.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Сборник задач к урокам информатики по теме «измерение и кодирование информации»
Категория:
Информатика
05.07.2023 13:18
Просмотр содержимого документа
«Сборник задач к урокам информатики по теме «измерение и кодирование информации»»
Сборник задач
к урокам информатики
по темЕ
«Измерение и Кодирование информации»
.
Златоуст, 2022 г
Сборник задач с решениями предназначен для учеников 7-11 классов для приобретения теоретических знаний и практических навыков по курсу «ИНФОРМАТИКА и ИКТ».
В сборнике содержатся теоретический материал и задачи по следующим темам:
-
содержательный подход к измерению количества информации;
-
алфавитный подход к измерению количества информации;
-
вероятностный подход к измерению количества информации;
-
кодирование текстовой информации;
-
кодирование звуковой информации.
-
Содержание
Содержательный подход к измерению количества информации……4
Алфавитный подход к измерению количества информации………...8
Вероятностный подход к измерению количества информации……. 12
Кодирование текстовой информации....................................................16
Кодирование звуковой информации………………………………….. 20
Тема: Содержательный подход к измерению количества информации.Цели: 1.повторить определение информации, ее свойства, виды информации, единицы измерения количества информации, формулы содержательного подхода к измерению количества информации;
2. закрепить материал решением задач на данную тему.
Теоретическая часть.
Определение информации.
Информация- те сведения об объектах и явлениях окружающей среды, их параметрах, свойствах состоянии, которые уменьшают имеющуюся степень неопределенности, неполноты знаний о них.
-
Свойства информации:
-
Понятность;
-
Полезность;
-
Достоверность;
-
Актуальность;
-
Полнота;
-
Точность.
2.Виды информации.
Информация существует в виде:
-
Текстов, рисунков, чертежей, фотографий;
-
Световых и звуковых волн;
-
Радиоволн;
-
Электрических и нервных импульсов;
-
Магнитных записей;
-
Жестов и мимики;
-
Запахов и вкусовых ощущений;
-
Хромосом.
3.Единицы измерения информации.
В качестве единицы измерения количества информации используется 1 бит. Также используются следующие единицы:
1 байт = 8 бит;
1 килобайт (Кбайт, Кб) = 210 байт = 1024 байт;
1 мегабайт (Мбайт, Мб) = 210 Кбайт = 1024 Кбайт = 220 байт = 1048576 байт;
1 гигабайт (Гбайт, Гб) = 210 Мбайт = 1024 Мбайт = 220 Кбайт =230 байт = 1073741824 байт.
Существуют более крупнее единицы измерения количества информации, которые используются реже, чем перечисленные выше:
1 терабайт (Тбайт, Тб) = 210 Гбайт =1024 Гбайт = 220 Мбайт = 230 Кбайт = 240 байт ;
1 петабайт (Пбайт, Пб) = 210 Тбайт = 1024 Тбайт = 220 Гбайт = 230 Мбайт = 240 Кбайт = 250 байт
4.Содержательный подход к измерению количества информации.
Если в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных событий, то количество информации, заключенное в этом сообщении,- х бит- и число N связаны формулой: 2х = N, x = log2N.
Если N равно целой степени двойки, то такое уравнение можно решить «в уме». В противном случае для решения уравнений нужно воспользоваться таблицей, которая у каждого ученика лежит на столе.
Количество информации в сообщении об одном из N равновероятных событий: i = log2N.
Практическая часть
Задание 1.
По данным определениям отгадайте многозначное слово, которое в том числе является понятием информатики или компьютерным термином.
-
Железная, женская, формальная, диалектическая, индуктивная, дедуктивная, математическая, двузначная, многозначная.(Логика)
-
Своевременная, объективная, ложная, проверенная, полная, исчерпывающая, секретная, массовая, генетическая, газетная, телевизионная, научно-техническая. (Информация)
-
Текстовый, бинарный, графический, программный, системный, исполняемый, командный, пакетный, скрытый, архивный.(Файл)
-
Людские, природные, экономические, скрытые, аппаратные, программные, информационные, открытые, закрытые.(Ресурсы)
Задание 2.
В приведенных текстах идущие подряд буквы нескольких слов образуют виды информации. Найдите их.
(Для визуального восприятия тексты демонстрируются на экране через проектор.)
-
Я его привез в указанное место, но там никого не оказалось. (Звук)
-
Когда-то он работал в идеологическом отделе. (Видео)
-
Он сказал: «Пройдите к стене». (текст)
-
Оказалось, что граф и Казанова- одно и то же лицо. (Графика)
Задание 3.
Задача 1.
Была получена телеграмма: «Встречайте, вагон 7». Известно, что в составе поезда 16 вагонов. Какое количество информации было получено?
Решение.
2х = 16, х = 4 бита
Задача 2.
В школьной библиотеке 16 стеллажей с книгами. На каждом стеллаже- 8 полок. Библиотекарь сообщил Пете, что нужная ему книга находится на пятом стеллаже на третьей сверху полке. Какое количество информации библиотекарь передал Пете?
Решение
16*8 = 128 полок, 2х = 128, х = 7 бит
Задача 3.
При угадывании целого числа в диапазоне от 1 до N было получено 7 бит информации. Чему равно N? [2, с, 74].
Решение
27 = 128
Задача 4
При угадывании целого числа в некотором диапазоне было получено 6 бит информации. Сколько чисел содержит этот диапазон?
Решение
26= 64
Задача 5
Сообщение о том, что ваш друг живет на десятом этаже, несет 4 бита информации. Сколько этажей в доме?
Решение
24= 16 этажей
Задача 6.
Сообщение о том, что Петя живет во втором подъезде, несет 3 бита информации. Сколько подъездов в доме?
Решение.
23= 8 подъездов.
Задача 7
В коробке лежат 7 разноцветных карандашей. Какое количество информации содержит сообщение, что из коробки достали красный карандаш?
Решение.
2х=7, х = log27 = 2, 80735 бита.
Задача 8
Какое количество информации несет сообщение: «Встреча назначена на сентябрь»? [1, с. 157,]
Решение.
2х = 12, х = log212 = 3,58496 бита.
Задача 9
Решить уравнение: 8х бит = 32 Кб.
Решение
8х = 32*1024*8,
(23)х = 25*210*23,
23х = 218
3*х = 18
х = 6
Задача 10.
Решить систему уравнений: 2х=2 бит = 8у-5Кб,
22у-1 Мб = 16х-3 бит
Решение.
2х=2 = (23)у-5*210*23, х+2 = 3(у – 5)+13, х=2=3у-2,
22у-1*220*23=(24)х-3 2у-1+23=4(х-3) 2у=22=4х-12
у=5
х=11
Для самостоятельного решения.
1.Решить задачу:
Какое количество информации несет сообщение о том, что встреча состоится 15 января?
(2х=31,х= log231= 4,95420 бита)
Цели:1 познакомить учащихся с алфавитным подходом к измерению информации;
2. закрепить теоретический материал на примерах.
Теоретическая часть.
1.Алфавитный подход к измерению количества информации.
Алфавитный подход позволяет определить количество информации, заключенный в тексте.
Алфавит- множество символов, используемых при записи текста.
Мощность (размер) алфавита- полное количество символов в алфавите.
Будем использовать следующие обозначения:
N- мощность алфавита;
K - количество символов в тексте;
i- количество информации, которое несет каждый символ алфавита;
I- объем информации, содержащейся в тексте.
Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле:
i= log 2 N, или 2 i= N .
Если весь текст состоит из K символов, то при алфавитном подходе размер содержащейся в нем информации равен:
I= K* I = K* log2N
Для представления текста в компьютере используется алфавит из 256 символов. Значит один символ компьютерного текста несет в себе * бит ( 1 байт) информации, так как 28= 256.
Практическая часть
Пример.
Книга, набранная с помощью компьютера, содержит 150 страниц, на каждой странице – 40 строк, в каждой строке- 60 символов. Каков объем информации в книге?
Решение.
150*40*60= 360000- количество символов во всей книге. Если в компьютерном тексте 1 символ несет в себе 1 байт информации, то объем информации в книге равен 360000*1 байт 360000 байт. Переведем в другие единицы измерения:
360000:1024= 351, 5625 Кб,
351,5625: 1924= 0,34332275 Мб.
Ответ: Объем информации в книге составляет приблизительно 0,3 Мб.
Решение задач.
Задача 1.
Сколько килобайт составляет сообщение, содержащее 12288 бит?
Решение.
12288/8/1024= 1,5 Кб.
Задача 2
Можно ли уместить на одну дискету книгу, имеющую 432 страницы, причем на каждой странице этой книги 46 строк, а в каждой строке 62 символа?
Решение.
В книге 432*46*62= 1 232064 символа. Для кодирования 1 символа требуется 1 байт. Следовательно, объем информации всей книги равен 1232064 байт 1,17 Мб. Так как на дискету помещается 1,44 Мб, то книга может поместиться на одну дискету.
Задача 3.
Сообщение, записанное буквами из 64-символьного алфавита, содержит 20 символов. Какой объем информации оно несет? .[2, с. 76].
Решение.
2i= 64? i= 6 бит- количество информации, которое несет каждый символ, 20*6= 120 бит = 15 байт.
Задача 4
Одно племя имеет 32-символьный алфавит, а второе племя- 64-символьный алфавит. Вожди племен обменялись письмами. Письмо первого племени содержало 80 символов, а письмо второго племени- 70 символов. Сравните объем информации, содержащейся в письмах.
Решение.
Первое племя: 2i= 32? i= 5 бит- количество информации, которое несет каждый символ, 5*80= 400 бит.
Второе племя: 2i= 64? i= 6 бит- количество информации, которое несет каждый символ, 6*70= 420 бит.
Следовательно, письмо второго племени содержит больше информации.
Задача 5.
Информационное сообщение объемом 1,5 Кб содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение? [4, с. 34.]
Дано: I= 1,5 Кб, K= 3072 символа.
Найти: N-?
Решение.
I= 1,5 Кб = 1,5*1024*8= 12288 бит.
i= I/K = 12288/3072= 4 бита.
N= 2i = 24= 16 символов.
Задача 6.
Объем сообщения, содержащего 2048 символов, составил 1/512 мегабайта. Каков размер алфавита, с помощью которого записано сообщение?
Дано:K= 2048 символов, I= 1/512 Мб.
Найти: N-?
Решение.
I= 1/512 Мб = 1/512*1024*1024*8 = 16384 бит
i=I/K= 16384/2048 = 8 бит.
N = 2i = 28 = 256 символов.
Задача 7.
Сколько символов содержит сообщение, записанное с помощью 16-символьного алфавита, если объем этого сообщения составил 1/16 мегабайта? [2.c.76]
Дано: N =16 символов, I= 1/16 Мб.
Найти: К -?
Решение.
I= 1/16 Мб = 1.16*1024*1024*8= 524288, бит.
N= 16= 2i, I = 4 бита.
K= I/I = 524288/4 = 131072 символа
Задача 8.
Для записи сообщения использовался 64-символьный алфавит. Каждая страница содержит 30 строк. Все сообщение содержит 8775 байт информации и занимает 6 страниц. Сколько символов в строке?.
Дано: N = 64 символа, I = 8775 байт, строк- 30, страниц- 6.
Найти: количество символов в строке.
Решение.
I = 8775 байт = 8775*8 = 70200 бит.
N = 64 = 2i, I = 6 бит.
Объем информации одной страницы книги: I/ количество страниц = 70200 бит/6 = 11700 бит.
Количество символов в строке: 11700 бит/6 бит/30 строк = 65 символов.
Задача 9.
Сообщение занимает 2 страницы и содержит 1/16 килобайта информации. На каждой странице записано 256 символов. Какова мощность использованного алфавита?
Дано: I = 1/16 Кб, страниц- 2, одна страница- 356 символов.
Найти: N-?
Решение.
I = 1/16 Кб = 1/16*1024*8= 512 бит.
K = 256*2= 512 символов на двух страницах.
I = I/K = 512/512 = 1 бит.
N = 2i = 21= 2 символа.
Для самостоятельного решения.
Решить задачу:
ДНК человека (генетический код) можно представить себе как некоторое слово в четырехбуквенном алфавите, где каждой буквой помечается звено цепи ДНК (нуклеотид). Сколько информации ( в битах) содержит цепочка ДНК человека, содержащая примерно 1,5*1023 нуклеотидов? [25 с. 77,]
Дано: N = 4, K = 1,5*1023.
Найти: I-?
Решение
N = 4 = 2i, I = 2 бита
I = K* I = 1,5*1023*2 = 3*1023 бит
Тема: Вероятностный подход к измерению количества информации.Цели:1. познакомить учащихся с формулой подсчета вероятности события, формулой Шеннона для подсчета количества информации в случае различных вероятностей событий;
2. закрепить теорию решением задач.
Теоретическая часть
1.Вероятностный подход к измерению количества информации.
Введем формулу подсчета вероятности интересующего нас события.
Пусть N – общее число возможных исходов какого-то процесса, из них интересующее нас событие может произойти K раз. Тогда вероятность p этого события равна:
p= K/N
Вероятность выражается в долях единицы. В частном случае вероятность достоверного события равна 1.
2.Практическая часть
Пример 1.
В барабане имеется 50 шаров. Из них 40 белых и 10 черных. Какова вероятность того, что выпадет белый шар? черный шар?
Решение
Обозначим вероятность выпадения белого шара pб, вероятность выпадения черного шара- pч. Тогда
pч = 10/50 = 0,2;
pб = 40/50 = 0,8
Пример 2.
В пруду живут 8000 карасей, 2000 щук, 40000 пескарей. Найти вероятность попадания на удочку каждой рыбки.
Решение
Всего в пруду
-
+2000+40000=50000 рыб.
pк = 8000/50000= 0,16;
pщ = 2000/50000 = 0,04;
pп = 40000/50000 = 0,8.
Количественная зависимость между вероятностью события p и количеством информации в сообщении о нем I выражается формулой:
I = log21/p
Вернемся, к примеру, 1 и определим количество информации в сообщении о выпадении белого и черного шара.
Iб = log21/0,8 = log21,25 = 0,321928;
Iч = log21/0, 2 = log25 = 2,321928.
Существуют ситуации, когда события имеют различные вероятности реализации. Например, когда мы рассматривали алфавитный подход к определению количества информации, то допускали, что все символы алфавита встречаются в тексте с одинаковой частотой (вероятностью). На самом деле, если посмотреть частотный словарь русского языка, мы заметим, что различные буквы в произвольном тексте встречаются с разными вероятностями. Например, наиболее часто встречаемая буква - О.
| Символ | Частота | Символ | Частота | Символ | Частота | Символ | Частота |
| О | 0,090 | в | 0,035 | я | 0,018 | ж | 0,007 |
| е, ё | 0,072 | к | 0,028 | ы, з | 0,016 | ю, ш. | 0,006 |
| а, и | 0,062 | м | 0,026 | ь, ъ, б | 0,014 | ц, щ, э | 0,003 |
| т, н | 0,053 | д | 0,025 | ч | 0,013 | ф | 0,002 |
| с | 0,045 | п | 0,023 | й | 0,012 |
|
|
| р | 0,040 | у | 0,021 | х | 0,009 |
|
|
Формулу для подсчета количества информации в случае различных вероятностей событий предложил К.Шеннон в 1948 г.:
I =∑log21/pi
где I – количество информации;
N - количество возможных событий;
pi – вероятность i-го события.
2.Решение задач.
Задача 1.
В корзине лежат 8 черных, 24 белых шара. Сколько информации несет сообщение о том, что достали черный шар?
Решение
pч = 8/32 =1/4, iч = log24 = 2 бита
Задача 2
В корзине лежат 32 клубка шерсти, среди них 4 красных. Сколько информации несет сообщение о том, что достали клубок красной шерсти?
Решение.
pк = 4/32 = 1/8,
iк = log28 = 3 бита
Задача 3
В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш, несет 4 бита информации. Сколько белых карандашей в коробке?
Решение
iб = log21/p = 4 бита, 1/p = 16, p = 1/16.
Пусть x- количество карандашей в коробке. Так как p = K/N, то есть x/64 = 1/16, то x = 4.
Задача 4
В ящике лежат перчатки – белые и черные, среди них 2 пары черных. Сообщение о том, что из ящика достали пару черных перчаток, несет 4 бита информации. Сколько всего пар перчаток было в ящике?
Решение
iч = log21/pч = 4 бита, 1/pч= 16, p = 1/16.
Пусть Х- общее количество пар перчаток. Так как p = K/N, то есть 2/Х = 1/16, то Х = 32.
Задача 5
В классе 30 человек. За контрольную работу по математике получено 6 пятерок, 15 четверок, 8 троек и 1 двойка. Какое количество информации в сообщении о том, что Иванов получил четверку.
Решение
p4 = K/N, p4 = 15/30 = ½, iч = log21/p4 = log22 = 1бит.
Задача 6
Известно, что в ящике лежат 20 шаров. Из них 10 – черных, 5 – белых, 4 – желтых и 1 красный. Какое количество информации несут сообщения о том, что из ящика случайным образом достали черный шар? белый шар? желтый шар? и красный шар?
Решение
pч = 10/20 = ½ , iч = log22 = 1 бит;
рб = 5/20 = 1/4, iб = log2 4 = 2 бита;
pж = 4/20 = 1/5, iж = log2 5 = 2,32193 бита;
ркр = 1/20, iч = log220 = 4,32193 бита.
Задача 7
За четверть ученик получил 100 оценок. Сообщение о том, что он получит четверку, несет 2 бита информации. Сколько четверок ученик получил за четверть?
Решение
iч = log21/p4 = 2 бита, следовательно, 1/р4 = 4, р4 = ¼.
Пусть Х – количество четверок за четверть, тогда Х/100 = ¼, Х = 25.
Задача 8
Для ремонта школы использовали белую, синюю и коричневую краску. Израсходовали одинаковое количество банок белой и синей краски. Сообщение о том, что закончилась банка белой краски, несет 2 бита информации. Синей краски израсходовали 8 банок. Сколько банок коричневой краски израсходовали на ремонт школы?
Решение
Iб = log21/pб = 2 бита, 1/рб = 4, р4 = ¼.
Пусть х – общее количество банок, тогда 8/х = ¼, х = 32 банки, 32-(8+8) = 16 банок с коричневой краской.
Задача 9
В корзине лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Сколько всего в корзине шаров?
Решение
iб = log21/pб = 2 бита, 1/рб = 4, р4 = ¼.
Пусть х – количество белых шаров, тогда х/18+х = ¼, 4х = 18+х, 3х = 18, х = 6 белых шаров, 18+6 = 24 шара всего в корзине.
3. Для самостоятельного решения.
1. Решить задачу:
На остановке останавливаются автобусы с разными номерами. Сообщение о том, что к остановке подошел автобус с номером 1, несет 4 бита информации. Вероятность появления на остановке автобуса с номером 2 в два раза меньше, чем вероятность появления автобуса с номером 1. Сколько информации несет сообщение о появлении на остановке автобуса с номером 2?
Решение
i1 = log21/p1= 4 бита, 1/р1 = 16, р1 = 1/16.
Но так как вероятность появления на остановке автобуса с номером 2 в два раза меньше, чем вероятность появления автобуса с номером 1, то р2 = р1/2 = 1/32, i2 = log21/p2 = log232 = 5 бит.
Цели: 1.познакомить учащихся с кодированием текстовой информации 2. 2.закрепить теоретический материал на примерах.
Изучаемые вопросы:
-
Объем памяти, занимаемый текстом;
-
Кодирование (декодирование) текстовой информации:
-
Внутреннее представление текста в компьютере.
Теоретическая часть
1.Объем памяти, занимаемый текстом.
В задачах данного типа используются понятия алфавит, мощность алфавита, символ, единицы измерения информации (бит, байт и др.)
Для представления текстовой (символьной) информации в компьютере используется алфавит мощностью 256 символов. Один символ такого алфавита несет 8 бит информации (28 = 256), т.е. двоичный код каждого символа в компьютерном тексте занимает 1 байт памяти.
Кодирование (декодирование) текстовой информации.
В задачах такого типа используются следующие понятия:
Кодирование - отражение дискретного (прерывного, импульсного) сообщения в виде определенных сочетаний символов;
Код (от фран. Code – кодекс, свод законов) – правило, по которому выполняется кодирование;
Кодовая таблица (кодовая страница) - таблица, устанавливающая соответствие между символами алфавита и двоичными числами.
В задачах используются следующие кодовые таблицы (имеются на компакт – диске к учебнику [12]) .
Примечание Задачи решаются с использованием кодовая таблица ASCII:
2.Практическая часть
Задача1.
Сколько бит памяти займет слово «микропроцессор»? [1, с. 131, пример1]
Решение.
Слово состоит из 14 букв. Каждая буква – символ компьютерного алфавита – занимает 1 байт памяти. Следовательно, слово занимает: 14 байтов = 14 * 8 = 112 бит памяти.
Ответ: 112 бит.
Задача 2.
Текст занимает 0,25 Кб памяти компьютера. Сколько символов содержит этот текст?
Решение.
Переведем килобайты в байты: 0,25 * 1024 = 256 байтов. Так как текст занимает 256 байтов, а каждый символ – 1 байт, то в тексте 256 символов.
Ответ: 256 символов.
Задача 3.
Текст занимает полных 5 страниц. На каждой странице размещается 30 строк по 70 символов в строке. Какой объем оперативной памяти (в байтах ) займет текст?
Решение.
30 * 70 * 5 = 10500 символов в тексте на страницах, т.е. займет 10500 байтов оперативной памяти.
Ответ:10500 ,байтов
Задача 4.
Считая, что каждый символ кодируется,1 байтом, оцените информационный объем
следующего предложения из пушкинского четверостишия: «Певец Давид был ростом мал, Но повалил же Голиафа! (ЕГЭ 2005 г., демонстрационная версия уровень А.)
а) 400 бит .
б) 50 бит
в) 400 байтов
г) б байтов
Решение.
В тексте 50 символов, включая пробелы и знаки препинания. При кодировании
каждого символа одним байтом на символ будет приходиться по 8 бит. Следовательно,
информационный объем предложения(переведем в биты): 50 *8=400 бит.
Ответ: 400 бит.
Задача 5.
Считая, что каждый символ кодируется 1 байтом, оцените информацией объем следующего предложения в кодировке КОИ-8: «Сегодня метеорологи предсказывали дождь. (ЕГЭ 2005 г., уровень А.)
а) 250 бит
б) 320 бит
в) 320 байт
г) 40 бит
Решение.
В предложении 40 символов. В таблице КОИ-8 каждый символ закодирован с помощью 1 байта, т. е. 8 битами. Следовательно, информационный объем предложения: 40 * 8 = 320 бит.
Ответ: 320 бит.
Задача 6.
Считая, что каждый символ кодируется 16 битами, оцените информацией объем следующего предложения в кодировке Unicode: «Каждый символ кодируй 8 битами. (ЕГЭ 2005 г., уровень А.)
а) 34 бита
в) 704 бита
г) 544 бита
Решение.
В предложении 34 символа. Следовательно, информационный объем предложения: 3418 = 544 бита.
Задача 7.
Текст занимает полных 10 секторов на односторонней дискете объемом 180. Дискета разбита на 40 дорожек по 9 секторов. Сколько символов содержит текст?
Решение.
Секторов на дискете: 40 * 9 = 360. В одном секторе поместится информации:
180 : 360 = 0.5 Кб. Текст содержит следующее количество байтов (символов) : 0.5 * 10 * 1024 = 5120.
Ответ: 5120 символов.
Задача 8.
Сообщение передано в семибитном коде. Каков его информационный объем в байтах, если известно, что передано 2000 символов?
Решение.
Если код символа содержит 7 бит, а всего 2000 символов, все сообщение займет 2000 * 7 бит = 14000 бит.
Переведем результат в байты : 14000 : 8 = 1750 байтов.
Ответ: 1750 байтов.
Задача 9.
Сколько секунд потребуется модему, передающему сообщение со скоростью 28800 бит / с, чтобы передать 100 страниц текста в 30 строк по 60 символов каждая, при условии, что каждый символ кодируется 1 байтом? (ЕГЭ 2005., уровень В.)
Решение.
Объем сообщения: 100 * 30 * 60 * = 1440000 бит. Найдем время передачи сообщения модемом: 1440000 бит : 28800 бит / с = 50 с.
Ответ: 50 с.
Задача 10.
Сколько секунд потребуется модему, передающему сообщение со скоростью 14400 бит / с, чтобы передать сообщение объемом 225 Кб? (ЕГЭ 2005., уровень В.)
Решение.
Переведем 225 Кб в биты: 225 * 1024 * 8 = 1843200 бит. Найдем врем я передачи сообщения модемом: 1843200 бит : 14400 бит / с = 128 с.
Ответ: 50 с
Предложенные задачи соответствуют различным уровням сложности:
Уровень1: задачи№1-№6
Уровень2 : задачи№7-№8
Уровень 3: задачи№9-№10.
Цели: 1.познакомить учащихся с кодированием звуковой информации 2. закрепить теоретический материал на примерах.
Изучаемые вопросы:
В сборнике рассматриваются задачи по темам:
-
Размер цифрового аудиофайла (моно и стерео)
-
Определение качества звука
-
Двоичное кодирование звука
1.Теоретическая часть
При решении задач учащиеся опираются на следующие понятия:
Временная дискретизация – процесс, при котором во время кодирования непрерывного звукового сигнала звуковая волна разбивается на отдельные маленькие временные участки, причем для каждого участка устанавливается определенная величина амплитуды. Чем больше амплитуда сигнала, тем громче звук.
Глубина звука (глубина кодирования) – количество бит на кодировку звука.
Уровни громкости (уровни сигнала) – звук может иметь различные уровни громкости. Количество различных уровней громкости рассчитываем по формуле N = 2i , где I – глубина звука.
Частота дискретизации – количество измерений уровня входного сигнала в единицу времени (за 1 секунду). Чем больше частота дискретизации, тем точнее процедура двоичного кодирования. Частота измерения в герцах (Гц). 1 измерение за 1 секунду – 1 Гц, 1000 измерений за 1 секунду – 1 кГц. Обозначим частоту дискретизации буквой D. Для кодирования выбирают одну из трех частот: 44,1 кГц, 22,05 кГц, 11,025 кГц. Считается, что диапазон частот, которые слышит человек, составляет от 20 Гц до 20 кГц.
Качество двоичного кодирования – величина, которая определяется глубиной кодирования и частотой дискретизации.
Аудиоадптер (звуковая плата) – устройство, преобразующие электрические колебания звуковой частоты в числовой двоичный код при вводе звука и из числового кода в электрические колебания при воспроизведении звука.
Характеристика аудиоадаптера – частота дискретизации и разрядность регистра.
Разрядность регистра – число бит в регистре аудиоадаптера. Чем больше разрядность, тем меньше погрешность каждого отдельного преобразования величины электрического тока в число и обратно. Если разрядность равна I, то при измерении входного сигнала может быть получено 2 = N различных значений.
2.Практическая часть
Пример
Размер цифрового моноаудиофайла А (в битах) измеряется по формуле:
A = D * T * I ,
Где D – частота дискретизации (Гц), Т – время звучания или записи звука, I – разрядность регистра (разрешение).
Размер цифрового стереооаудиофайла (А) измеряется по формуле:
A = 2 * D * T * I ,
сигнал записан для двух колонок, так как раздельно кодируются левый и правый каналы звучания.
| Тип сигнала | Частота дискретизации, кГц | ||
|
| 44,1 | 22,05 | 11,25 |
| 16 бит, стерео | 10,1 Мб | 5,05 Мб | 2,52 Мб |
| 16 бит, моно | 5,05 Мб | 2,52 Мб | 1,26 Мб |
| 8 бит, моно | 2,52 | 1,26 Мб | 630 Кб |
|
|
|
|
|
Решение.
Из формулы А =D * Т* I получаем формулу для расчета длительности звучания:
Т = А / D / I.
5,25 Мб = 5505024 байта,
22,05 кГц - 22050 Гц,
Т =5505024 байта : 22050 Гц ; 2 байта = 124,8 с.
Ответ. 124,8 с.
Решение задач
Задача 1.
Одна минута записи цифрового аудиофайла занимает на диске 1,3 Мб, разрядность звуковой платы — 8. С какой частотой дискретизации записан звук? [1, с. 157,]
Решение.
Из формулы А =D* Т * I получаем формулу для расчета частоты дискретизации:
D = A/T/I
1,3 Мб = 1363148,8. байта,
D = 1363148,8 байта : 60 с : 1 байт = 22719,1Д Гц = 22,05 кГц,
Ответ, 22,05 кГц.
Задача 2.
Две минуты записи цифрового аудиофайла занимают на диске 5,1 Мб. Частота дискретизации — 22050 Гц. Какова разрядность аудиоадаптера? [1, с. 157,]
Решение,
Из формулы А = D*Т* I получаем формулу для расчета разрядности: 5,1 Мб = 5347737,6 байта,
I =5347737,6 байта : 120 с : 22050 Гц =2,02 байта =16 бит.
Ответ: 16 бит.
Задета 3.
Объем свободной памяти на диске — 0,01 Гб, разрядность звуковой платы — 16. Какова длительность звучания цифрового аудиофайла, записанного с частотой дискретизации 44100 Гц? [1, с. 157;]
Решение.
0,01 Гб = 10737418,24 байта,
Т = 10737418,24 байта : 44100 Гц : 2 байта = 121,74 с = 2,03 мин.
Ответ, 2,03 мин.
Задача 4.
Оцените информационный объем моноаудиофайла длительностью звучания 1 мин, если глубина кодирования и частота дискретизации звукового сигнала равны соответственно:
а.) 16 бит и 8 кГц;
б) 16 бит и 24 кГц [2, с. 76].
Решение.
а) Информационный объем звукового файла, длительностью 1 с равен: 16 бит * 8000 = 128000 бит = 16000 байт = 15,625 Кб. Информационный объем звукового файла длительностью 1 мин равен: 15,625 Кб/с*60 с = 937,5 Кб.
б) Информационный объем звукового файла длительностью 1 с равен: 16 бит * 24000 = 384000 бит = 48000 байт = 46,875 Кб.
Задача 5.
Определите размер (в байтах) цифрового аудиофайла, время звучания которого составляет 10 секунд при частот дискретизации 22,05 кГц и разрешении 8 бит. Файл сжатию не подвержен [1, с. 158].
Решение.
22,05 кГц = 22,05 * 1000 Гц = 22050 Гц.
А = D *Т*I / 8 = 22050 Гц* 10 с* 8 бит / 8 = 220500 байт.
Ответ. 220500 байт.
Зaдaчa 6.
Определите объем памяти для хранения цифрового аудиофайла, время звучания которого составляет 2 минуты при частоте дискретизации 44,1 кГц и разрешении 16 бит [1. с. 157].
Решение.
44,1 кГц = 44,1*1000 Гц = 44100 Гц,
2 мин =2 * 60 с=120 с,
А =D * Т* I / 8=44100 Гц * 120 с * 16 бит / 8 = 10584000 байт = 10335,9375 Кб =10,094 Мб.
Ответ. 10 Мб.
Задача 7.
В распоряжении пользователя имеется память объемом 2.6 Мб Необходимо записать цифровой аудиофайл с 'длительностью звучании 1 минута, Каковы должны быть частота дискретизации и разрядность? [1, с. 157,]
Решение.
Из формулы А = D * Т* I получаем формулу для расчета частоты дискретизации и разрядности: D*I=A/T
. 2,6 Мб = 2726297,6 байта,
D*I=A/T= 2726297,6 байта : 60 с = 45438,3 байта, D=45438,8 байта : I.
Разрядность адаптера может быть 8 или 16 бит (1 байт или 2 байта). Поэтому частота дискретизации может быть либо 45438*3 Гц =44Д кГц — стандартная характерная частота дискретизации, либо 22719,15 Гц =22,05 кГц — стандартная характерная частота дискретизации,
Ответ.
|
| Частота дискретизации | Разрядность аудиоадаптера |
| Вариант 1 | 22,05 кГц | 16 бит |
| Вариант 2 | 44,1 кГц | 8 бит |
Задача 8.
Объем, свободной памяти на диске — "5,25 Мб, разрядность звуковой платы 16.Какова- длительность звучания цифрового аудиофайла, записанного с частотой дискретизации 22,05 кГц? [ 1, с, 157.]
Уровень «3» («4*, «5») означает, что, правильно решив предложенную задачу, ученик может претендовать на получение оценки * 8* (« 4 *, * 5* соответственно),
Информационный объем звукового файла длительностью 1 мин равен: 46,875 Кб/с* 60 с =2812,5 Кб = 2,8 Мб.
Ответы, а) 987,5 Кб; б) 2,8 Мб.
При решении задач используется таблица на е. 51.
Задача 9.
Какой объем памяти требуется для хранения цифрового аудиофайла с записью звука высокого качества при условии» что..время звучания составляет3 мин? [ 1, с.'157,']
Решение.
Высокое качество звучания достигается при частоте дискретизации 44,1 кГц и разрядности аудиоадаптера, равной 16.
А = 180 с * 2 байта*44100 Гц = 15876000 байт =15,1 Мб,
Ответ. 15,1 Мб
Задача 10.
Цифровой аудиофайл, содержит запись звука низкого качества (звук мрачный и приглушенный). Какова длительность звучания файла, если его объем составляет 650 Кб? [1, с. 157,]
Решение.
Для мрачного и приглушенного звука характерны следующие параметры: частота дискретизации — 11,025 кГц, разрядность аудиоадаптера .— 8 бит.
T = А /D/I.
. 650 Кб = 665600 байт.
Т= 665600 байт / 11025 Гц / 1 байт =60,4 с.
Ответ. 60,4 с.
Задача 11.
Оцените информационный объем высокачествекного стереоаудиофайла длительностью звучания. 1 мим, если глубина кодирования 16 бит, а частота дискретизации
48 кГц [2, с, 74].
Решение.
информационный объем звукового файла длительностью 1 с равен: 16 бит * 48000 * 2 = 1536000 бит=187,5 Кб (умножили на 2, так как стерео), информационный объем звукового файла длительностью 1 мин равен: 187,5 Кб/с* 60 с= 11 Мб.
Ответ. 11 Мб.
Задача 12.
Рассчитайте время звучания моноаудиофайла, если при 16-битном кодировании и частоте дискретизации 32 кГц его объем равен:
а) 700 Кб;
б) 6300 Кб .[2, с. 76].
Решение.
а) Информационный объем звукового файла длительностью 1 с равен: 16 бит * 32000 = 512000 бит = 64000 байт =62,5 Кб. Время звучания моноаудиофайла объемом 700 Кб равно:
700 Кб : 62,5 Кб/с = 11,2 с.
б)Информационный объем звукового файла длительностью 1с равен:
16 бит *32000 = 512000 бит = 64000 байт = 62,5 Кб.
Время звучания моноаудиофайла объемом 6300 Кб равно: 6300 Кб : 62,5 Кб с= 100,8 с=1,68 мин.
Ответ: а) 11,2 с; б) 1,68 м.
Задача 13.
Вычислите, сколько байт информации на занимает на компа кт-диске одна секунда тереозаписи (частота 44032 Гц 16 бит на значение). Сколько занимает одна минута?
Какова максимальная емкость диска (считая максимальную длительность равен 80 мин)? [4, с. 34.]
Решение.
A = 1 c*2 байта-*44082 Гц = 88064 байта (1 с стереозаписи на компакт-диске
60 с* 2 байта* 44082 Гц=5283840 байт (1мин. стереозаписи на компакт-диске
4800 с *2 байта*44032 Гц = 422707200=412800 Кб=403,125 Мб (80 мин).
Ответ. 88064 байта (1 с). 5283840 байт (1 мин), 403,125 Мб (80 мин).
Определение качества звука
Для определения качества звука надо найти частоту дискретизации и воспользоваться таблицей на с.51.
256 (28) уровней интенсивности сигнала - качество звучания радиотрансляции,
65536 (216) уровней интенсивности сигнала качество звучания аудио-СD.Самая качественная частота соответствует музыке, записанной на компакт-диске. Величина алогового сигнала в этом случае - 44100 раз в секунду.
Задача 14.
Определите качество звука (качество радиотрансляции, среднее качество, качество аудио-CD),если известно, что объем моноаудиофайла длительностью звучания
10 с равен:
а) 940 Кб;
б)157 Кб [2.c.76]
Решение.
а) 940 Кб = 962560 байт = 7700480 бит,
700480 бит : 10 с = 770048 бит/с,
70048 бит/с : 16 бит = 48128 Гц — частота дискретизации близка к самой той —44,1кГц
б) 157 Кб = 160768 байт = 1286144 бита,
1286144 бита : 10 с = 128614,4 бита/с,
128614,4 бита/с : 16 бит = 8038,4 Гц,
. Ответы: a)Качество аудио- СD): б) качество радиотрансляции.
Задача 15.
Определите длительность звукового файла , который уместится на гибкой дискете 3,5. Учтите, что для хранения данных на такой дискете выделяется 2847 секторов объемов 512 байт.
а) при низком качестве звука: моно, 8 бит, 48 кГц;
б) при высоком качестве звука: стерео, 16 бит, 48 кГц [2.c.77]
а) Информационный объем дискеты равен:
2847*512 байт = 1457664 байт =1423,5 Кб.
Информационный объем звукового файла длительностью 1 с равен:
8 бит=8000 =64000 бит =8000 байт =7,8 Кб.
Время звучания моноаудиофайла объемом 1423?5 Кб равно: 1423,5 Кб ; 7,8 Кб/с =182,5 с = 3 мин.
б) Информационный объем дискеты равен:
2847 * 512 байт = 1457664 байт= 1428,5 Кб.
Информационный объем звукового файла длительностью 1 с равен:
16 бит*48000*2 = 1536000 бит =192000 байт =187,5 Кб. Время звучания cетереоаудиофайла объемом 1423,5 Кб равно:
1423,5 Кб : 187,5 Кб/с =7,6 с.
Ответы. а) 8 мин, б) 7,6 с.
(ультракоротковолновых) радиопередач.
Задача 16.
Аналоговый звуковой сигнал был дискретизирован сначала е использованием 256 уровней интенсивности сигнала (качество звучания радиотрансляции), а затем с использованием 65536 уровней интенсивности сигнала (качество звучания аудио-СD), Во сколько раз различаются информационные объемы оцифрованного звука? [25 с. 77,]
Решение.
Длина кода аналогового сигнала с использованием 256 уровней интенсивности сигнала равна 8 битам, с использованием 65536 уровней интенсивности сигнала 16 битам, Так как длина кода одного сигнала увеличилась вдвое, то информационные объемы: оцифрованного звука различаются в 2 раза.
Ответ. В 2 раза.
Задача 17.
Согласно теореме Найквиста-Котелъникова, для того чтобы аналоговый сигнал молено было точно восстановить но его дискретному представлению. Частота дискретизации должна быть как минимум вдвое больше максимальной звуковой частоты этого сигнала. Какова должна быть частота .дискретизации звука, воспринимаемого человеком? Что должно быть больше: частота дискретизации речи или частота дискретизации звучания симфонического оркестра?
Ответ.
Считается, что диапазон частот, которые слышит человек, составляет от 20 Гц до 20 кГц. Таким образом, аппаратура и программные средства должны обеспечивать частоту дискретизации не менее 40 кГц. Компьютерная обработка звучания симфонического оркестра предполагает более высокую частоту дискретизации, чем обработка речи, поскольку диапазон частот в первом случае значительно больше.
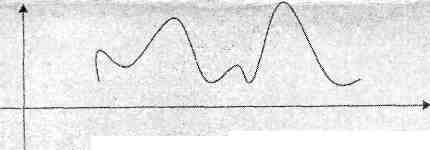
Задача 18.
На рисунке изображено зафиксированное самописцем звучание 1 с речи» Закодируйте его в двоичном: цифровом коде с частотой 10 Гц и длиной кода 3 бита.
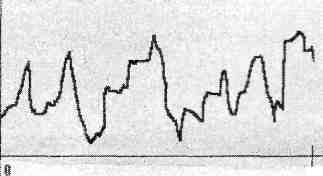
Решение.
Кодирование с частотой 10 Гц означает, что мы должны измерить высоту звука. 10 раз за секунду/Выберем равноотстоящие моменты времени:
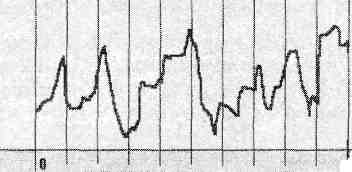
Длина когда 3 бита означает 28 = 8 уровней квантования. То есть в качестве числового кода высота звука в каждой выбранный момент времени мы можем задать одну из следующих комбинаций : 000, 001, 011, 100, 101, 110, 111. Их всего 8,
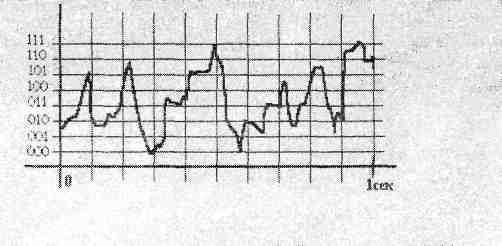
следовательно, высоту звука можно измерять на 8 уровнях.
«Округлять» значение высота звука будем до ближайшего нижнего уровня:
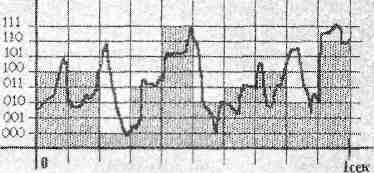
Используя данный способ кодирования, мы получим следующий результат (пробелы поставлены для удобства восприятия):
100 100 000 011 111 010 011 100 010 110.
Задача 19.
Объясните, почему уровень квантования относится, наряду с частотой дискретизации, к основным характеристикам представления звука в компьютере.
Ответ.
В геометрии, физике, технике есть понятие «точность измерения», тесно связанное с понятием- «погрешность измерения». Но есть и понятие «точность представления»
Например, про рост человека можно сказать, что он:
a) около 2 м.
б) чуть больше 1,7 м, в) равен 1 м 72 см, и равен 1 м 71 см 8 мм. То есть для
обозначения измеренного роста можно использовать 1, 2, 3 или 4 цифры.
Так же и для двоичного кодирования. Если для записи высоты звука в конкретный момент времени использовать только 2 бита, то, даже если измерения были точны, передать можно только 4 уровня: низкий (00), ниже среднего (01), выше среднего (10), высокий (11). Если использовать 1 байт, то можно передать 256 уровней. Чем выше уровень квантования, или, что то же самое, чем больше битов отводится для записи измеренного значения, тем- точнее передается это значение.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
