Задания школьного этапа всероссийской олимпиады школьников
в 2018-2019 учебном году
5 класс
1. Восстановите запись: * *
+ * *
--------
1 9 7
2. Разрежьте прямоугольник размером 4 * 8 на девять квадратов.
3.Три землекопа за два часа выкопали три ямы.
Сколько ям выкопают шесть землекопов за пять часов?
4. На улице, встав в кружок, беседуют четыре девочки: Аня, Валя, Галя и Надя. Девочка в зеленом платье (не Аня и не Валя) стоит между девочкой в голубом платье и Надей. Девочка в белом платье стоит между девочкой в розовом платье и Валей. Платье какого цвета носит каждая девочка?
5.В квадратном ковре со стороной 1 м моль проела 51 дырку (дырка — точка). Докажите, что некоторой квадратной заплаткой со стороной 20 см можно закрыть не менее трёх дырок.
6 класс
1.Найдите все решения ребуса (одинаковые буквы соответствуют одинаковым цифрам, а различные буквы зашифрованы различными цифрами)
КНИГА + КНИГА + КНИГА = НАУКА
2. На листе в клетку нарисован прямоугольник 6×7. Разрежьте его по линиям сетки на 5 каких-нибудь квадратов.
3. Волк, Ёж, Чиж и Бобёр делили апельсин. Ежу досталось вдвое больше долек, чем Чижу, Чижу – впятеро меньше, чем Бобру, а Бобру – на 8 долек больше, чем Чижу. Найдите, сколько долек было в апельсине, если Волку досталась только кожура.
4. Среднее арифметическое четырех чисел равно 10. Если вычеркнуть первое из этих чисел, то среднее арифметическое оставшихся трех увеличится на 1, если вместо первого числа вычеркнуть второе число, то среднее арифметическое оставшихся чисел увеличится на 2, а если вычеркнуть только третье число, то среднее арифметическое оставшихся увеличится на 3. На сколько изменится среднее арифметическое трех оставшихся чисел, если вычеркнуть четвертое число?
5. В обменном пункте совершаются операции двух типов: 1) дай 2 евро – получи 3 доллара и конфету в подарок; 2) дай 5 долларов – получи 3 евро и конфету в подарок. Когда богатенький Буратино пришел в обменник, у него были только доллары. Когда ушел – долларов стало поменьше, евро так и не появились, зато он получил 50 конфет. Во сколько долларов обошелся Буратино такой "подарок"?
6. Когда три подруги — Надя, Валя и Маша — вышли гулять, на них были белое, красное и синее платья. Туфли их были тех же трех цветов, но только у Нади цвета туфель и платья совпадали. При этом у Вали ни платье, ни туфли не были синими, а Маша была в красных туфлях. Определите цвет платьев и туфель каждой из подруг.
7 класс
Решите уравнение: |2011-x| = 2012
Переложите одну из 7 спичек числа ��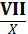
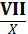 так, чтобы получилась дробь
так, чтобы получилась дробь
Котенок Малыш может облизать себя с головы до кончика хвоста за полчаса, а кот Тоша может облизать Малыша за 5 минут. Себя Тоша способен помыть за 20 минут. Сколько времени придется трудиться Малышу, чтобы помыть Тошу?
Мальчики в классе составляют 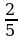 учащихся всего класса.
учащихся всего класса. 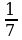 их числа составляют отличники. Сколько в классе девочек?
их числа составляют отличники. Сколько в классе девочек?
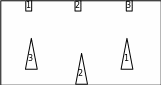
Соедините попарно фигуры, имеющие одинаковую нумерацию, произвольными непрерывными линиями таким образом, чтобы эти линии не пересекались друг с другом.
8 класс
8.1. Найдите последнюю цифру числа 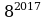
8.2. Разложите на множители 4(��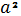
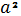 +��
+��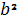
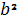 )+21 ��
)+21 ��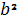
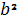 -20 ab- 36
-20 ab- 36
8.3. Дан правильный треугольник АВС. На продолжении стороны АС за точку С взята точка D, а на продолжении стороны ВС за точку С - точка Е так, что ВD=DE. Докажите, что АD=СE.
8.4. Известно, что 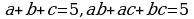 . Чему может равняться
. Чему может равняться 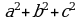 ?
?
8.5. Из листа бумаги вырезали произвольный треугольник. Можно ли так загнуть три его угла, чтобы оставшаяся часть треугольника оказалась накрытой без просветов и наложений?
9 класс
1. Решить уравнение: 2х² + y² + 2xy + 2x + 1= 0
2. Некто купил лошадь и спустя некоторое время продал ее за 24 пистоля. При этой продаже он теряет столько процентов , сколько стоила лошадь. Спрашивается, за какую сумму он ее купил?
3. Известно, что a + b + c = 5, ab + ac + bc = 5. Чему может равняться a² + b² + c² ?
4. Через середину гипотенузы прямоугольного треугольника проведен перпендикуляр. Отрезок этого перпендикуляра, заключенный внутри треугольника равен 3 см, а вне треугольника( до пересечения с продолжением другого катета) равен 9 см. Найти длину гипотенузы.
5.Найти два трехзначных числа, зная, что их сумма кратна 498, а частное кратно 5.
10 класс
1. Тридцать девочек – 13 в красных платьях и 17 в синих платьях – водили хоровод вокруг новогодней ёлки. Впоследствии каждую из них спросили, была ли её соседка справа в синем платье. Оказалось, что правильно ответили те и только те девочки, которые стояли между девочками в платьях одного цвета. Сколько девочек могли ответить утвердительно?
2. Точки M и N – середины сторон AB и CD соответственно четырёхугольника ABCD. Известно, что BC || AD и AN = CM. Верно ли, что ABCD – параллелограмм?
3. Для различных положительных чисел а и b выполняется равенство 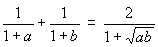 . Докажите, что а и b – взаимно обратные числа.
. Докажите, что а и b – взаимно обратные числа.
4. Решить уравнение 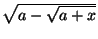 = x.
= x.
5. В треугольнике ABC точка I — центр вписанной окружности. Точки M и N — середины сторон BC и AC соответственно. Известно, что угол AIN прямой. Докажите, что угол BIM — также прямой.
11 класс
1.Решите уравнение
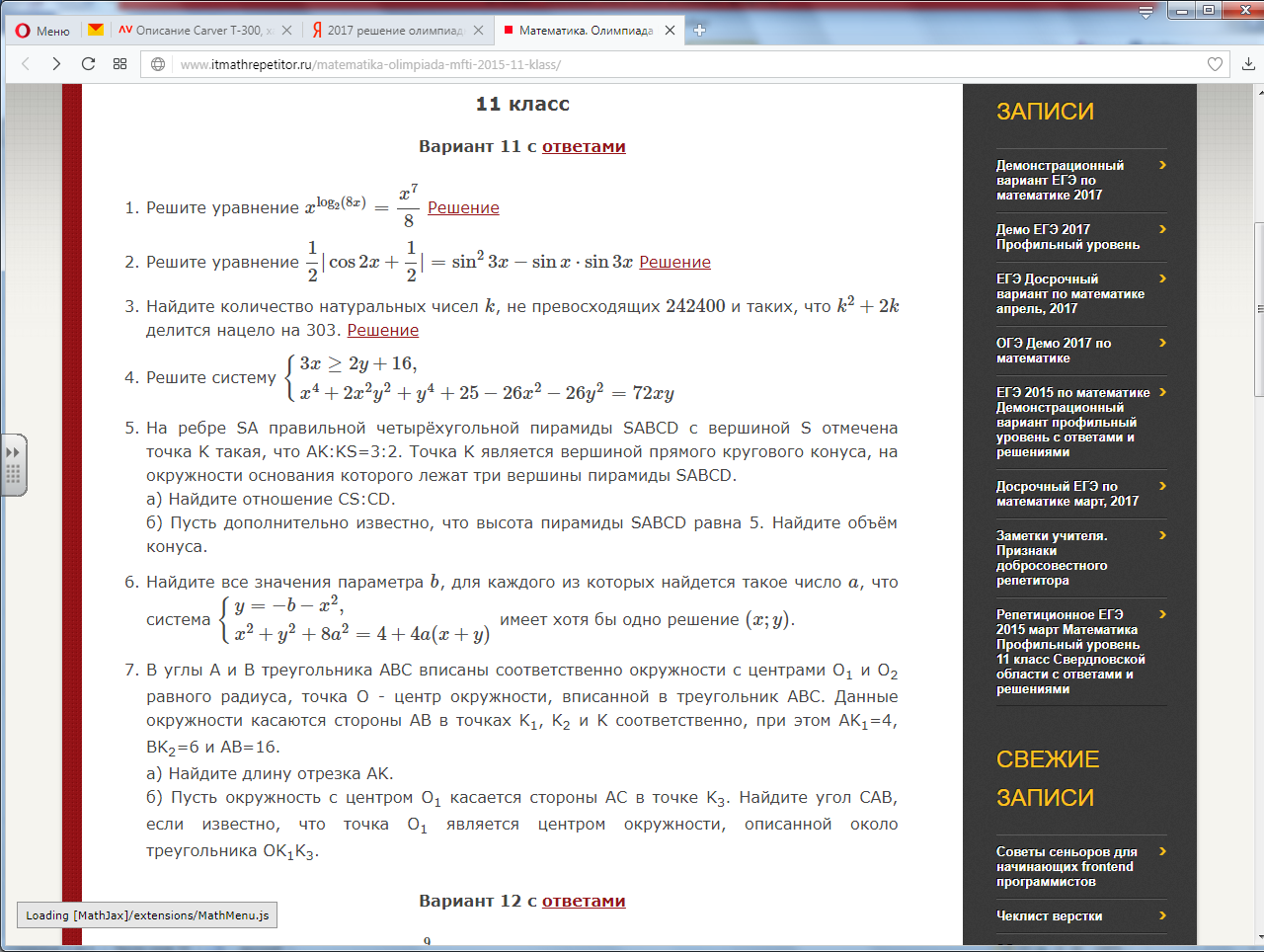
2.Приведите пример числа х, для которого выполняется равенство. Ответ обоснуйте.

3. Решите в натуральных числах неравенство: 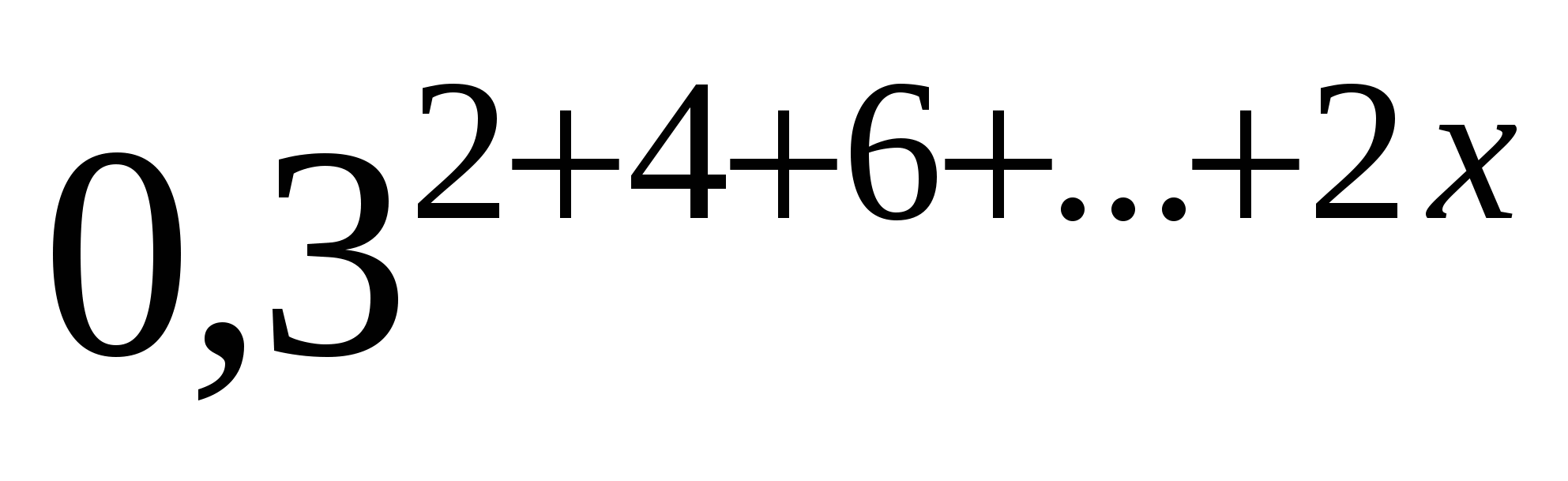
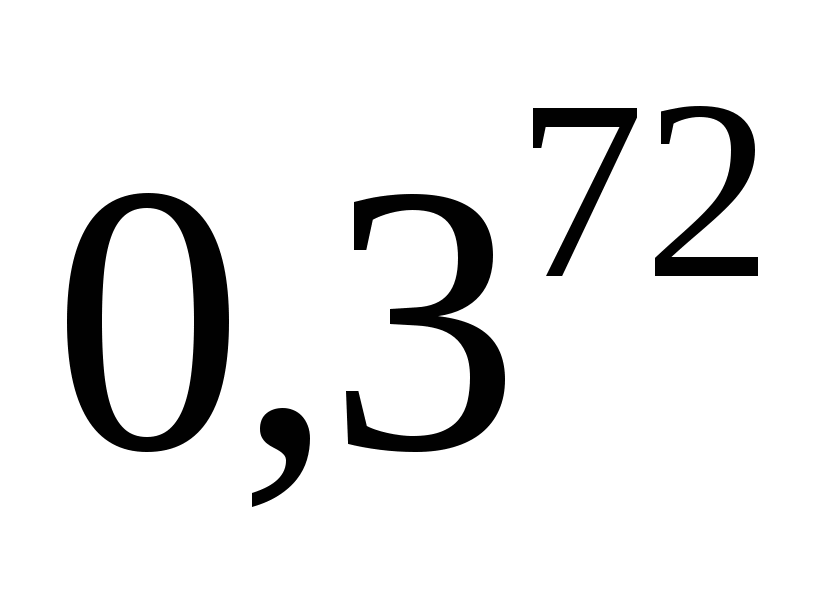
4. Сфера проходит через вершины одной грани куба и касается сторон противоположной грани куба. Найдите отношение объёма сферы к объёму куба.
5. Фальшивомонетчик дядя Коля за 10 дней изготовил 2014 фальшивых пятитысячных монет. Его внук Петя с целью оптимизации работы деда рассчитал производительность труда (количество монет, изготовленных за k подряд идущих дней, деленное на k) для всех k = 1,2,…,10 и всех этапов производства. Докажите, что произведение всех полученных Петей 45 чисел – целое число.







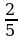 учащихся всего класса.
учащихся всего класса. 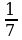 их числа составляют отличники. Сколько в классе девочек?
их числа составляют отличники. Сколько в классе девочек?
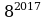
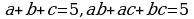 . Чему может равняться
. Чему может равняться 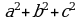 ?
?










