Низикова Зоя Константиновна
Преподаватель математики
ГБОУ СПО «Трубчевский
политехнический техникум»
СИММЕТРИЯ В АЛГЕБРЕ.
СИММЕТРИЧЕСКИЕ МНОГОЧЛЕНЫ.
В окружающем нас мире господствует симметрия. Живая природа представляет нам многочисленные примеры симметрии. Способ существования живого организма и принцип минимальности (экономичности) определяет его вид симметрии (зеркальную, осевую, поворотную).
Образы симметрии встречаются и в неживой природе - это устройство небесных тел, кристаллов, молекул и других тел, и обусловлено это физическими законами.
Радуют глаз своей соразмерностью великолепные архитектурные сооружения, замечательные произведения искусства. Руками человека создано множество симметричных предметов-дома, машины, мебель, почти все предметы нашего обихода.
Симметрия с её пропорциональностью и уравновешенностью, служит основой прочности всего созданного, структурной необходимостью организмов и устройств.
Симметрия – неотъемлимая часть нашей жизни. Она везде вокруг нас, мы настолько привыкли к ее существованию, что не всегда замечаем красоту и изящество, которые симметрия придает нашей жизни.
Один из великих математиков 20 века Герман Вейль писал, что «симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство».
Открытие красоты опытных наук, количественное описание физического мира, методы описания преобразований дает нам математика. В математике рассматриваются различные виды симметрий. Все они имеют свое название. Большинство из нас знакомо с такими понятиями как центральная симметрия, осевая симметрия, зеркальная симметрия. Надо отметить, что многие симметрии можно увидеть только с помощью сложнейших математических построений и преобразований. В одном из разделов Математики-Алгебры симметрия используется в записи чисел (101, 303, 54045, 245606542), треугольнике Паскаля, Биноме Ньютона, в работе с понятиями четная или нечетная функция, обратная функция, при исследовании и построении графиков этих функций.
В линейной Алгебре широко используется симметрия матриц, и таких примеров можно привести множество. Свойства симметрии позволяет облегчить исследования и уменьшить объем вычислений.
Симметрия в широком смысле - это неизменность при каких-либо преобразованиях. Рассмотрим симметрию в Алгебре на примере решения симметрических уравнений.
При решении некоторых алгебраических уравнений высшего порядка и некоторых систем алгебраических уравнений используются специальные многочлены, которые называются симметрическими.
Простейшие симметрические многочлены 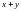 и
и 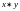 . Легко видеть, что замене
. Легко видеть, что замене  на
на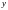 и
и 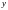
на  многочлены не меняет. По определению многочлен
многочлены не меняет. По определению многочлен 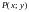 от двух переменных называется симметрическим, если при замене
от двух переменных называется симметрическим, если при замене  на
на 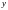 и
и 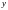 на
на  он не меняется, например :
он не меняется, например :
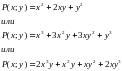

Легко видеть, что при замене  на
на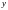 и
и 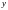 на
на  имеет место тождество
имеет место тождество 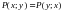 , то говорит о том что эти многочлены являются симметрическими.
, то говорит о том что эти многочлены являются симметрическими.
Теория симметрических многочленов очень проста и позволяет решать не только многие системы алгебраических уравнений, но и различные другие алгебраические задачи (решение иррациональных уравнений, доказательство тождеств и неравенств, разложение на множители и так да
С помощью теории сим
 метрических многочленов решение задач заметно упрощается, и, что самое главное, проводится стандартным приемом.
метрических многочленов решение задач заметно упрощается, и, что самое главное, проводится стандартным приемом.
Существует простой прием получать симметрические многочлены. Возьмем любой многочлен от и и подставим в него в место и их выражения через  и
и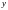 . Ясно что при этом мы получаем симметрический многочлен т.к. ни
. Ясно что при этом мы получаем симметрический многочлен т.к. ни 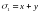 , ни
, ни 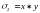 не меняются при перестановке
не меняются при перестановке  и
и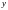 местами, потому и не меняется и получившийся многочлен, выражающийся через
местами, потому и не меняется и получившийся многочлен, выражающийся через 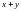 и
и 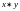 например:
например:
Получить симметрический многочлен из 

Доказано, что любой симметрический многочлен можно представить в виде многочлена от  и
и  . Это позволяет весьма просто решать различные системы уравнений. Часто встречаются симметрические системы уравнений, т.е такие, где оба уравнения системы являются симметричными многочленами от
. Это позволяет весьма просто решать различные системы уравнений. Часто встречаются симметрические системы уравнений, т.е такие, где оба уравнения системы являются симметричными многочленами от  и
и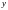 . В этом случаем удобно перейти к новым неизвестным
. В этом случаем удобно перейти к новым неизвестным 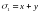 и
и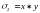 что всегда возможно.
что всегда возможно.
Такая замена неизвестных приводит к понижению степени уравнений и решение системы относительно новых неизвестных  и
и  упрощенно.
упрощенно.
После нахождения значения величин  и
и  нужно иметь ввиду, что квадратное уравнение
нужно иметь ввиду, что квадратное уравнение  и системе уравнений
и системе уравнений  связаны между собой следующим образом:
связаны между собой следующим образом:
если  корни квадратного уравнения, то система имеет 2 решения
корни квадратного уравнения, то система имеет 2 решения
и других решений не имеет. Обратно, если  -решение системы, то числа
-решение системы, то числа  и
и являются корнями квадратного уравнения.
являются корнями квадратного уравнения.
Например: Решить систему уравнений введем новые неизвестные  ,
,
 т.к
т.к  , то получаем новую систему из этой системы уравнений получаем
, то получаем новую систему из этой системы уравнений получаем  = итак
= итак 
 , т.е для первоначальных неизвестных
, т.е для первоначальных неизвестных  и
и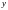 мы получаем следующую систему уравнений , которая легко решается, т.к. она сводится к решению уравнения
мы получаем следующую систему уравнений , которая легко решается, т.к. она сводится к решению уравнения  и получаем следующие решение первоначальной системы
и получаем следующие решение первоначальной системы
Симметрических многочленов с успехом решается целая серия задач, в которых выражения, содержащие корни заданного квадратного уравнения. Например: Составить квадратное уравнение, корнями которого являются квадраты корней уравнения 
Обозначим корни данного уравнения через  и
и  , корни искомого уравнения-через
, корни искомого уравнения-через  и
и  , а коэффициенты искомого уравнения-через p и q.
, а коэффициенты искомого уравнения-через p и q.
По Теореме Виета:

И точно также 
По условию задачи имеем 
 и потому
и потому
Таким образом, искомое квадратное уравнение имеет вид 
Таким же приемом решаются и более сложные задачи.
Ещё области применения симметрических многочленов - доказательство многих неравенств, решение возвратных уравнений, решение систем уравнений с тремя неизвестными, освобождение от иррациональности в знаменателе, решение уравнений высших степеней, извлечение корней.
На примере симметрических многочленов мы увидели. Что симметрия в широком смысле-это неизменность при каких либо преобразованиях .Математики из давно стремились к красоте математических формул и справедливо считали, что красивая формула отличается от некрасивой тем, что в красоте больше симметрии.
Мы видим, что симметрия в Алгебре не только делает преобразования красивым, но и значительно облегчает вычислительную работу.
Список использованной литературы
1 В.Г. Болтянский, Н.Я Веленкин Симметрия в алгебре –М. Наука 2002 г.
2 Вайтроб А.Ю. Симметрия{Текст} / А.Ю. Вайнтроб, А.Б. Сосинский// Квант. -1984. -№3. – С.19-22.
3 Вейль Г. Симметрия {Текст} / Г. Вейль. – М.: Наука, 1998. – 123 с., ил.
4 Виленкин Н.Я. За страницами учебника математики {Текст} / Н.Я. Виленкин, Л.П. Шибасов, 3. Ф. Шибасова. – М.: Просвещение, 1996.-288с.
5 Депман И.Я. За страницами учебника математики {Текст}/ И.Я. Депман, Н.Я. Виленкин. –М.: Просвещение, 1989. -276 с.
6 Колосов А.А. Книга для внекласного чтения по математике {Текст}/ А.А. Колосов. – М.: Наука, 2008. -187 с.
7 http://www.aeli.altai.ru/nauka
8 http://www.5ballov.ru
9 http://www.ru.wikipedia.org
10 http://www.hist-singhts.ru
11 http://www.museum.ru






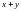 и
и 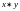 . Легко видеть, что замене
. Легко видеть, что замене  на
на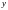 и
и 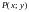 от двух переменных называется симметрическим, если при замене
от двух переменных называется симметрическим, если при замене 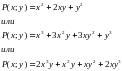

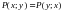 , то говорит о том что эти многочлены являются симметрическими.
, то говорит о том что эти многочлены являются симметрическими.
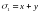 , ни
, ни 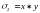 не меняются при перестановке
не меняются при перестановке 









