Итоговая аттестация по математике
для обучающихся 9 классов (для детей с ЗПР)
Цель проведения итоговой аттестации – установление соответствия уровня и качества подготовки обучающихся 9-х классов по математике в объеме, установленном обязательным минимумом содержания основного общего образования государственного образовательного стандарта.
Итоговая аттестация по математике в 9 классе проводится в форме контрольной работы в двух вариантах - 7 заданий по математике, алгебре, 3 задания по геометрии.
Продолжительность работы- по 45 мин.
Работа охватывает содержание, включенное в УМК:
С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин, Математика 5-6 класс;
Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова. Алгебра 7-9 класс;
Л.С. Атанасян. В.Ф.Бутузов, С.Б.Кажомцев, Э.Г.Позняк, И.И.Юдина. Геометрия 7-9 класс.
Оценивание контрольной работы с учётом планируемых результатов.
| № | Планируемые результаты | Балл |
| 1 | Уметь выполнять вычисления и преобразования. | 1 |
| 2 | Уметь решать уравнения, неравенства и их системы. | 1 |
| 3 | Уметь выполнять преобразования алгебраических выражений | 1 |
| 4 | Уметь строить и читать графики функций. | 1 |
| 5 | Уметь решать уравнения, неравенства и их системы. | 1 |
| 6 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами. | 1 |
| 7 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами. | 1 |
| 8 | Уметь проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения. | 1 |
| 9 | Уметь решать несложные практические расчётные задачи, связанные с отношением, пропорциональностью величин, дробями, процентами; пользоваться оценкой и прикидкой при практических расчётах; интерпретировать результаты решения задач с учётом ограничений, связанных с реальными свойствами рассматриваемых объектов. | 1 |
| 10 | Уметь решать практические задачи, требующие систематического перебора вариантов; сравнивать шансы наступления случайных событий, оценивать случайного события, сопоставлять и исследовать модели реальной ситуации с использованием аппарата вероятности и статистики. | 1 |
Шкала пересчёта балла в оценку по пятибалльной шкале.
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Общий балл | 0-2 | 3-5 | 6-8 | 9-10 |
Вариант 1
Найдите значение выражения:  ;
;
Найдите корень уравнения: 7(х+6)=8х ;
Найдите значение выражения: (а-2)² +а(4+7а) при  ;
;
Установите соответствие между функциями и их графиками.
Функции
1)  2)
2)  3)
3)  4)
4) 
Графики
А) Б) В)

Ответ:
Укажите решение неравенства

 ;
;
Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь треугольника.
Отрезки АС и ВD – диаметры окружности с центром О. Угол АСВ равен 53°. Найдите угол АОD. Ответ дайте в градусах.
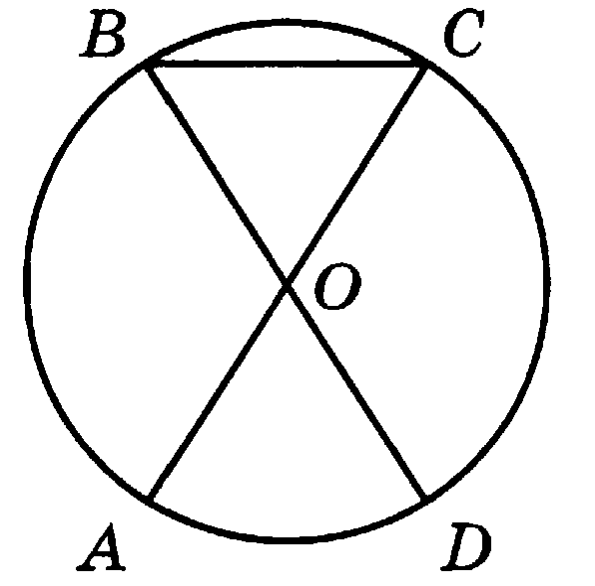
Какие из утверждений верны?
Каждая из биссектрис равнобедренного треугольника является его высотой.
Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом.
Все диаметры одной и той же окружности равны между собой.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Городской бюджет составляет 14 млн рублей, а расходы на одну из его статей составили 45%. Сколько рублей потрачено на эту статью бюджета?
В среднем из 500 аккумуляторов, поступивших в продажу в магазин «Светлячок», 21 неисправны. Найдите вероятность того, что один купленный аккумулятор окажется исправным.
Вариант 2
Найдите значение выражения:  ;
;
Найдите корень уравнения: 6х+1= - 4х ;
Найдите значение выражения: (2+с)² -с(с-4) при  ;
;
Установите соответствие между функциями и их графиками.
Функции
 2)
2)  3)
3)  4)
4)  - 1
- 1
Графики
А) Б) В)

Ответ:
Укажите решение неравенства


В прямоугольном треугольнике катет и гипотенуза равны соответственно 9 и 41. Найдите другой катет этого треугольника.
В окружности с центром О отрезки АС и ВD – диаметры. Угол АОD равен 108°. Найдите угол АСВ. Ответ дайте в градусах.
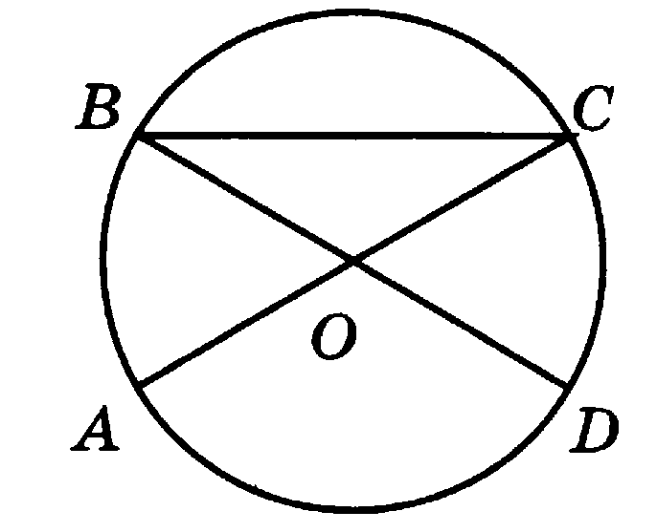
Какое из следующих утверждений верно?
Смежные углы всегда равны.
Через заданную точку плоскости можно провести единственную прямую.
Диагонали ромба точкой пересечения делятся пополам.
В ответ запишите номер выбранного утверждения.
Магазин детских товаров «Детский мир» закупает погремушки по оптовой цене 190 рублей за одну штуку и продаёт с 20-процентной наценкой. Сколько рублей будут стоить 3 такие погремушки, купленные в этом магазине?
На тарелке 10 пирожков: 5 с мясом, 2 с капустой и 3 с вишней. Саша наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.





 ;
; ;
; 2)
2)  3)
3)  4)
4) 


 ;
; 
 ;
;  ;
; 2)
2)  3)
3)  4)
4)  - 1
- 1 













