
Занимательные тесты по курсу
«ОБЫКНОВЕННЫЕ ДРОБИ»
Учитель математики Сумбаева Елена Анатольевна

Методические рекомендации
Управляющие кнопки
Помощь (повторить теорию)
«Далее» (следующий вопрос)
«Вернуться назад» (возврат на предыдущий слайд)
«В начало» (возвращение на слайд список тем)

Обыкновенные дроби
1. Окружность и круг
2. Доли. Обыкновенные дроби
3. Сравнение дробей
4. Правильные и неправильные дроби
5. Сложение и вычитание дробей с одинаковыми
знаменателями
6. Деление и дроби
7. Смешанные числа
8. Сложение и вычитание смешанных чисел
Методические рекомендации

Какие из точек на
рисунке лежат на
окружности?
а) K, L, O, B
б) B
в) A, M, C
г) B, A, C, M

Окружность это линия на плоскости каждая точка,
которой расположена на одинаковом расстоянии
от центра окружности. Это расстояние называется
радиус и в записях обозначается буквой R . Центр
окружности обозначают буквой O .
Окружность разделяет плоскость на две части, внутреннюю и внешнею. Внутренняя часть называется кругом. Точка O — это центр и круга и окружности.
Отрезки OA , OB , и OC — это радиусы, их длины равны. Отрезок BC , проходящий через центр окружности (круга) называется диаметр и обозначается буквой d . Диаметр разделяет круг на два полукруга , а окружность на две полуокружности .
Точки A и B делят окружность на две части, которые называются дугами, а точки A и B концами этих дуг .
Точки A, E лежат внутри круга. Точки F, C лежат вне круга.
Точки B, D лежат на окружности.

Чем является на
рисунке ОС ?
а) центр окружности
б) радиус
в) диаметр
г) хорда

Окружность это линия на плоскости каждая точка,
которой расположена на одинаковом расстоянии
от центра окружности. Это расстояние называется
радиус и в записях обозначается буквой R . Центр
окружности обозначают буквой O .
Окружность разделяет плоскость на две части, внутреннюю и внешнею. Внутренняя часть называется кругом. Точка O — это центр и круга и окружности.
Отрезки OA , OB , и OC — это радиусы, их длины равны. Отрезок BC , проходящий через центр окружности (круга) называется диаметр и обозначается буквой d . Диаметр разделяет круг на два полукруга , а окружность на две полуокружности .
Точки A и B делят окружность на две части, которые называются дугами, а точки A и B концами этих дуг .
Точки A, E лежат внутри круга. Точки F, C лежат вне круга.
Точки B, D лежат на окружности.

Чем является на
рисунке МС ?
а) отрезок
б) дуга
в) диаметр
г) хорда

Окружность это линия на плоскости каждая точка,
которой расположена на одинаковом расстоянии
от центра окружности. Это расстояние называется
радиус и в записях обозначается буквой R . Центр
окружности обозначают буквой O .
Окружность разделяет плоскость на две части, внутреннюю и внешнею. Внутренняя часть называется кругом. Точка O — это центр и круга и окружности.
Отрезки OA , OB , и OC — это радиусы, их длины равны. Отрезок BC , проходящий через центр окружности (круга) называется диаметр и обозначается буквой d . Диаметр разделяет круг на два полукруга , а окружность на две полуокружности .
Точки A и B делят окружность на две части, которые называются дугами, а точки A и B концами этих дуг .
Точки A, E лежат внутри круга. Точки F, C лежат вне круга.
Точки B, D лежат на окружности.

Какие из точек на
рисунке лежат
внутри круга?
а) А, С, М
б) К, О, L
в) В
г) В, А, С, М, К

Окружность это линия на плоскости каждая точка,
которой расположена на одинаковом расстоянии
от центра окружности. Это расстояние называется
радиус и в записях обозначается буквой R . Центр
окружности обозначают буквой O .
Окружность разделяет плоскость на две части, внутреннюю и внешнею. Внутренняя часть называется кругом. Точка O — это центр и круга и окружности.
Отрезки OA , OB , и OC — это радиусы, их длины равны. Отрезок BC , проходящий через центр окружности (круга) называется диаметр и обозначается буквой d . Диаметр разделяет круг на два полукруга , а окружность на две полуокружности .
Точки A и B делят окружность на две части, которые называются дугами, а точки A и B концами этих дуг .
Точки A, E лежат внутри круга. Точки F, C лежат вне круга.
Точки B, D лежат на окружности.

Чем является на
рисунке ВС?
а) диаметр и хорда
б) радиус
в) диаметр
г) хорда

Окружность это линия на плоскости каждая точка,
которой расположена на одинаковом расстоянии
от центра окружности. Это расстояние называется
радиус и в записях обозначается буквой R . Центр
окружности обозначают буквой O .
Окружность разделяет плоскость на две части, внутреннюю и внешнею. Внутренняя часть называется кругом. Точка O — это центр и круга и окружности.
Отрезки OA , OB , и OC — это радиусы, их длины равны. Отрезок BC , проходящий через центр окружности (круга) называется диаметр и обозначается буквой d . Диаметр разделяет круг на два полукруга , а окружность на две полуокружности .
Точки A и B делят окружность на две части, которые называются дугами, а точки A и B концами этих дуг .
Точки A, E лежат внутри круга. Точки F, C лежат вне круга.
Точки B, D лежат на окружности.

Проверь себя
1.б, 2.б, 3.б,
4.б, 5. а
Оценка
«5» – верных ответов 5
«4» - верных ответов 4
«3» – верных ответов 3
«2» – верных ответов 1-2
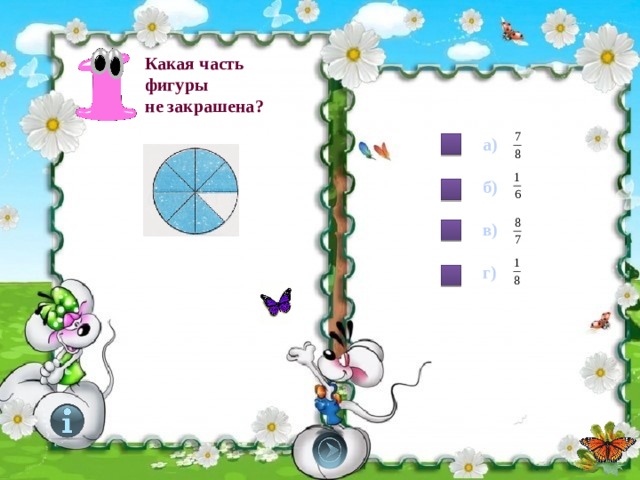
Какая часть
фигуры
не закрашена?
а)
б)
в)
г)

Давайте разрежем яблоко на 4 равные части. Эти части в математике называют долями . Яблоко разделили на 4 доли, значит каждая из них,
будет называться одной четвертой яблока.
Длина отрезка АВ равна 6 см. Значит 1см составляет
отрезка АВ. Долю называют половиной, - третью, - четвертью
- обыкновенная дробь . В дроби число 4 написанное сверху черты
называют числителем дроби, а число 6, написанное снизу
черты — знаменателем дроби. Знаменатель обозначает, на какое количество частей разделили , а числитель — сколько таких частей взято .
Дроби можно изображать на координатном луче. На рисунке изображены дроби
.Отрезок ОА равен
единичного отрезка ОЕ.
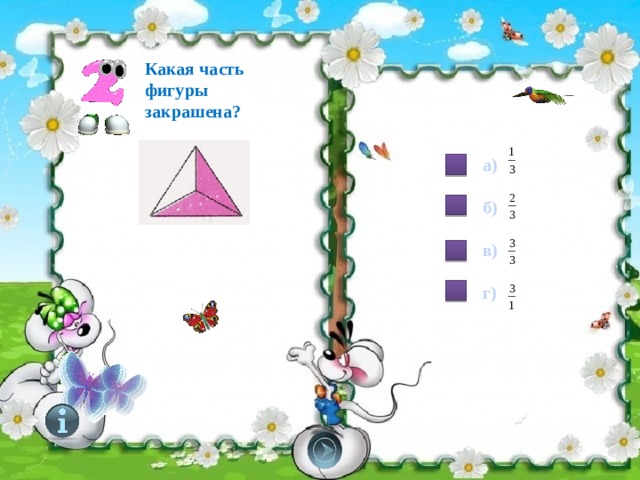
Какая часть фигуры закрашена?
а)
б)
в)
г)

Давайте разрежем яблоко на 4 равные части. Эти части в математике называют долями . Яблоко разделили на 4 доли, значит каждая из них,
будет называться одной четвертой яблока.
Длина отрезка АВ равна 6 см. Значит 1см составляет
отрезка АВ. Долю называют половиной, - третью, - четвертью
- обыкновенная дробь . В дроби число 4 написанное сверху черты
называют числителем дроби, а число 6, написанное снизу
черты — знаменателем дроби. Знаменатель обозначает, на какое количество частей разделили , а числитель — сколько таких частей взято .
Дроби можно изображать на координатном луче. На рисунке изображены дроби
.Отрезок ОА равен
единичного отрезка ОЕ.

Что показывает
числитель дроби?
а) число равных
частей
б) сколько равных
частей взяли
в) на сколько равных
частей разделили
г) число

Давайте разрежем яблоко на 4 равные части. Эти части в математике называют долями . Яблоко разделили на 4 доли, значит каждая из них,
будет называться одной четвертой яблока.
Длина отрезка АВ равна 6 см. Значит 1см составляет
отрезка АВ. Долю называют половиной, - третью, - четвертью
- обыкновенная дробь . В дроби число 4 написанное сверху черты
называют числителем дроби, а число 6, написанное снизу
черты — знаменателем дроби. Знаменатель обозначает, на какое количество частей разделили , а числитель — сколько таких частей взято .
Дроби можно изображать на координатном луче. На рисунке изображены дроби
.Отрезок ОА равен
единичного отрезка ОЕ.

Площадь поля
20 га. Тракторист
вспахал часть
всего поля.
Сколько гектаров
вспахал тракторист?
а) 80 га
б) 5 га
в) 4 га
г) 16 га

Давайте разрежем яблоко на 4 равные части. Эти части в математике называют долями . Яблоко разделили на 4 доли, значит каждая из них,
будет называться одной четвертой яблока.
Длина отрезка АВ равна 6 см. Значит 1см составляет
отрезка АВ. Долю называют половиной, - третью, - четвертью
- обыкновенная дробь . В дроби число 4 написанное сверху черты
называют числителем дроби, а число 6, написанное снизу
черты — знаменателем дроби. Знаменатель обозначает, на какое количество частей разделили , а числитель — сколько таких частей взято .
Дроби можно изображать на координатном луче. На рисунке изображены дроби
.Отрезок ОА равен
единичного отрезка ОЕ.
Турист прошел
6 км, что
составляет
всего пути. Какое
расстояние должен
пройти турист?
а) 2 км
б) 18 км
в) 3 км
г) 15 км

Давайте разрежем яблоко на 4 равные части. Эти части в математике называют долями . Яблоко разделили на 4 доли, значит каждая из них,
будет называться одной четвертой яблока.
Длина отрезка АВ равна 6 см. Значит 1см составляет
отрезка АВ. Долю называют половиной, - третью, - четвертью
- обыкновенная дробь . В дроби число 4 написанное сверху черты
называют числителем дроби, а число 6, написанное снизу
черты — знаменателем дроби. Знаменатель обозначает, на какое количество частей разделили , а числитель — сколько таких частей взято .
Дроби можно изображать на координатном луче. На рисунке изображены дроби
.Отрезок ОА равен
единичного отрезка ОЕ.

Проверь себя
1. г, 2. б, 3. б,
4. б, 5. б
Оценка
«5» – верных ответов 5
«4» - верных ответов 4
«3» – верных ответов 3
«2» – верных ответов 1-2

Какая из двух
точек лежит
на координатном
луче левее?
а) Х
Х( ) или У( )
б) У
в) равны

Найди точки
которые
совпадают
А( ) В( )
С( ) Д( )
а) А и В
б) А и С
в) С и Д
г) А и Д
 " width="640"
" width="640"
Сравните дроби
и
а)
б)
в)
=

 " width="640"
" width="640"
Сравните дроби
и
а)
б)
в)
=

Выберите из
данных дробей те,
которые
обозначают
половину:
а)
б)
в)
г)

Проверь себя
4. а 5. б
Оценка
«5» – верных ответов 5
«4» - верных ответов 4
«3» – верных ответов 3
«2» – верных ответов 1-2

При каких
значениях х
а) 5, 6, 7, 8, 9
б) 3, 4, 5, 7
дробь -
правильная?
в) 1, 2, 3, 4, 5, 6, 7, 8
г) 11, 10, 15, 23

Дробь, числитель которой меньше знаменателя , называется
правильной.
Дробь, числитель которой больше знаменателя или равен ему,
называется неправильной .
Правильная дробь меньше единицы , а неправильная дробь больше или равна единице

а) 1, 2, 3
б) 2, 3, 4, 5, 6, 7, 8, 9
в) 1, 4, 7, 9
Какую цифру можно поставить
вместо звездочки,
чтобы дробь
была неправильной?

Дробь, числитель которой меньше знаменателя , называется
правильной.
Дробь, числитель которой больше знаменателя или равен ему,
называется неправильной .
Правильная дробь меньше единицы , а неправильная дробь больше или равна единице
 и =" width="640"
и =" width="640"
Сравните дроби
а)
б)
в)
и
=

Дробь, числитель которой меньше знаменателя , называется
правильной.
Дробь, числитель которой больше знаменателя или равен ему,
называется неправильной .
Правильная дробь меньше единицы , а неправильная дробь больше или равна единице
 1 и 1 1 =" width="640"
1 и 1 1 =" width="640"
а)
б)
в)
1
Сравните
1
и
1
1
=

Дробь, числитель которой меньше знаменателя , называется
правильной.
Дробь, числитель которой больше знаменателя или равен ему,
называется неправильной .
Правильная дробь меньше единицы , а неправильная дробь больше или равна единице
 1 1 =" width="640"
1 1 =" width="640"
а)
б)
в)
1
Сравните
и
1
1
1
=

Дробь, числитель которой меньше знаменателя , называется
правильной.
Дробь, числитель которой больше знаменателя или равен ему,
называется неправильной .
Правильная дробь меньше единицы , а неправильная дробь больше или равна единице

Оценка
«5» – верных ответов 5, «4» - верных ответов 4
«3» – верных ответов 3, «2» – верных ответов 1-2
Проверь себя
4. а 5. а

Выполните действие: +
а) б)
в) г)

Нахождение части:
число : знаменатель * числитель
Нахождение целого:
число : числитель * знаменатель

Выполните действие: -
а) б)
в) г)

Нахождение части:
число : знаменатель * числитель
Нахождение целого:
число : числитель * знаменатель

Решите уравнение: - p =
а) б)
в) г)

Нахождение части:
число : знаменатель * числитель
Нахождение целого:
число : числитель * знаменатель

Выполните действия: ( - ) + ( - )
а) б)
в) г)

Нахождение части:
число : знаменатель * числитель
Нахождение целого:
число : числитель * знаменатель

Решите задачу:
Из помидоров массой кг и огурцов
массой кг сделали салат. Какова
масса салата?
а) б)
в) г)

Нахождение части:
число : знаменатель * числитель
Нахождение целого:
число : числитель * знаменатель

Проверь себя
1. б 2. в 3. а
4. г 5. б
Оценка
«5» – верных ответов 5
«4» - верных ответов 4
«3» – верных ответов 3
«2» – верных ответов 1-2

Решите уравнение: = 28
а) 336 б)
в) 356 г) 256

Черту дроби можно понимать как знак деления = 2 : 3
С помощью дробей можно записать результат деления двух любых натуральных чисел. Если деление выполняется нацело , то частное является натуральным числом. Если же разделить нацело нельзя , то частное является дробным числом. Например, 27 : 3 = = 9; 5 : 6 =
Любое натуральное число можно записать в виде дроби с любым натуральным знаменателем. Числитель этой дроби равен произведению числа и этого знаменателя. 3 =
Чтобы разделить сумму на число , можно разделить на это число каждое слагаемое и сложить полученные частные. 9603 : 3 = (9000 + 600 + 3) : 3 =
9000 : 3 + 600 : 3 + 3 : 3 =
3000 + 200 + 1 = 3201

За неделю израсходовано
3 кг сахара. Сколько
килограммов сахара в среднем
расходовали за один день?
а) 21 б)
в) г) 10

Черту дроби можно понимать как знак деления = 2 : 3
С помощью дробей можно записать результат деления двух любых натуральных чисел. Если деление выполняется нацело , то частное является натуральным числом. Если же разделить нацело нельзя , то частное является дробным числом. Например, 27 : 3 = = 9; 5 : 6 =
Любое натуральное число можно записать в виде дроби с любым натуральным знаменателем. Числитель этой дроби равен произведению числа и этого знаменателя. 3 =
Чтобы разделить сумму на число , можно разделить на это число каждое слагаемое и сложить полученные частные. 9603 : 3 = (9000 + 600 + 3) : 3 =
9000 : 3 + 600 : 3 + 3 : 3 =
3000 + 200 + 1 = 3201

Решите уравнение: = 7
а) 112 б) 123
в) 132 г) 121

Черту дроби можно понимать как знак деления = 2 : 3
С помощью дробей можно записать результат деления двух любых натуральных чисел. Если деление выполняется нацело , то частное является натуральным числом. Если же разделить нацело нельзя , то частное является дробным числом. Например, 27 : 3 = = 9; 5 : 6 =
Любое натуральное число можно записать в виде дроби с любым натуральным знаменателем. Числитель этой дроби равен произведению числа и этого знаменателя. 3 =
Чтобы разделить сумму на число , можно разделить на это число каждое слагаемое и сложить полученные частные. 9603 : 3 = (9000 + 600 + 3) : 3 =
9000 : 3 + 600 : 3 + 3 : 3 =
3000 + 200 + 1 = 3201

Выберите только те
частные, которые обозначают дробные числа
28 : 7, 1: 2, 2 : 1, 1 : 6, 12 : 12
а) 28 : 7 б) 12 : 12
в) 1 : 2, 1 : 6 г) 28 : 7, 2 : 1

Черту дроби можно понимать как знак деления = 2 : 3
С помощью дробей можно записать результат деления двух любых натуральных чисел. Если деление выполняется нацело , то частное является натуральным числом. Если же разделить нацело нельзя , то частное является дробным числом. Например, 27 : 3 = = 9; 5 : 6 =
Любое натуральное число можно записать в виде дроби с любым натуральным знаменателем. Числитель этой дроби равен произведению числа и этого знаменателя. 3 =
Чтобы разделить сумму на число , можно разделить на это число каждое слагаемое и сложить полученные частные. 9603 : 3 = (9000 + 600 + 3) : 3 =
9000 : 3 + 600 : 3 + 3 : 3 =
3000 + 200 + 1 = 3201

Найдите значение
выражения, применяя свойство
деления суммы на число
(48 + 80) : 16
а) 48 : 16 + 80 : 16 = 8
б) 128 : 16 = 8
в) (48 : 16) + 80 = 83
г) 48 + (80 : 16) = 53

Черту дроби можно понимать как знак деления = 2 : 3
С помощью дробей можно записать результат деления двух любых натуральных чисел. Если деление выполняется нацело , то частное является натуральным числом. Если же разделить нацело нельзя , то частное является дробным числом. Например, 27 : 3 = = 9; 5 : 6 =
Любое натуральное число можно записать в виде дроби с любым натуральным знаменателем. Числитель этой дроби равен произведению числа и этого знаменателя. 3 =
Чтобы разделить сумму на число , можно разделить на это число каждое слагаемое и сложить полученные частные. 9603 : 3 = (9000 + 600 + 3) : 3 =
9000 : 3 + 600 : 3 + 3 : 3 =
3000 + 200 + 1 = 3201

Проверь себя
1. а 2. б 3. б
4. в 5. а
Оценка
«5» – верных ответов 5
«4» - верных ответов 4
«3» – верных ответов 3
«2» – верных ответов 1-2

В каком ряду записаны
смешанные числа?
а) 1
б) 3
в) 4
г) 2
1)
2)
3)
4)


Какое действие
подразумевается
между целой частью и
дробной частью
смешанного числа?
а) умножение
б) деление
в) сложение
г) вычитание


Замените смешанное
число неправильной
дробью.
а)
б)
в)
г)


Скольким равна
целая часть если
дробь записать
в виде смешанного
числа?
а) 3
б) 2
в) 17
г) 4


У Винни-Пуха несколько
банок, вмещающих
по кг меда. Сколько
ему понадобится таких
банок, чтобы разлить в них
кг меда?
а) 12
б) 6
в) 13
г) 8


Проверь себя
1. а 2. б 3. б
4. в 5. а
Оценка
«5» – верных ответов 5
«4» - верных ответов 4
«3» – верных ответов 3
«2» – верных ответов 1-2

Выполните действие:
+
а)
б)
в)
г)

.
.
Сложение и вычитание смешанных чисел выполняется на основе этих действий.
Например:
При сложении (и вычитании) чисел в смешанной записи целые части складывают (вычитают) отдельно, а дробные — отдельно. Иногда при сложении смешанных чисел в их дробной части получается неправильная дробь. В этом случае из нее выделяют целую часть и добавляют ее к уже имеющейся целой части. Например: .
Если при вычитании смешанных чисел дробная часть уменьшаемого меньше дробной части вычитаемого, поступают так:
Таким же образом поступают и при вычитании дроби из натурального числа , и при вычитании смешанного числа из натурального числа. Например:

Выполните действие:
+
а)
б)
в)
г)

.
.
Сложение и вычитание смешанных чисел выполняется на основе этих действий.
Например:
При сложении (и вычитании) чисел в смешанной записи целые части складывают (вычитают) отдельно, а дробные — отдельно. Иногда при сложении смешанных чисел в их дробной части получается неправильная дробь. В этом случае из нее выделяют целую часть и добавляют ее к уже имеющейся целой части. Например: .
Если при вычитании смешанных чисел дробная часть уменьшаемого меньше дробной части вычитаемого, поступают так:
Таким же образом поступают и при вычитании дроби из натурального числа , и при вычитании смешанного числа из натурального числа. Например:

Выполните действие:
-
а)
б)
в)
г)

.
.
Сложение и вычитание смешанных чисел выполняется на основе этих действий.
Например:
При сложении (и вычитании) чисел в смешанной записи целые части складывают (вычитают) отдельно, а дробные — отдельно. Иногда при сложении смешанных чисел в их дробной части получается неправильная дробь. В этом случае из нее выделяют целую часть и добавляют ее к уже имеющейся целой части. Например: .
Если при вычитании смешанных чисел дробная часть уменьшаемого меньше дробной части вычитаемого, поступают так:
Таким же образом поступают и при вычитании дроби из натурального числа , и при вычитании смешанного числа из натурального числа. Например:

Выполните действие:
-
а)
б)
в)
г)

.
.
Сложение и вычитание смешанных чисел выполняется на основе этих действий.
Например:
При сложении (и вычитании) чисел в смешанной записи целые части складывают (вычитают) отдельно, а дробные — отдельно. Иногда при сложении смешанных чисел в их дробной части получается неправильная дробь. В этом случае из нее выделяют целую часть и добавляют ее к уже имеющейся целой части. Например: .
Если при вычитании смешанных чисел дробная часть уменьшаемого меньше дробной части вычитаемого, поступают так:
Таким же образом поступают и при вычитании дроби из натурального числа , и при вычитании смешанного числа из натурального числа. Например:

Выполните действие:
-
а)
б)
в)
г)

.
.
Сложение и вычитание смешанных чисел выполняется на основе этих действий.
Например:
При сложении (и вычитании) чисел в смешанной записи целые части складывают (вычитают) отдельно, а дробные — отдельно. Иногда при сложении смешанных чисел в их дробной части получается неправильная дробь. В этом случае из нее выделяют целую часть и добавляют ее к уже имеющейся целой части. Например: .
Если при вычитании смешанных чисел дробная часть уменьшаемого меньше дробной части вычитаемого, поступают так:
Таким же образом поступают и при вычитании дроби из натурального числа , и при вычитании смешанного числа из натурального числа. Например:

Проверь
себя
Оценка
«5» – верных ответов 5
«4» - верных ответов 4
«3» – верных ответов 3
«2» – верных ответов 1-2
1.а, 2. г, 3. б,
4. а, 5. в

СПАСИБО ЗА УЧАСТИЕ!!!!




































 " width="640"
" width="640"

 " width="640"
" width="640"








 и =" width="640"
и =" width="640"

 1 и 1 1 =" width="640"
1 и 1 1 =" width="640"

 1 1 =" width="640"
1 1 =" width="640"

























































