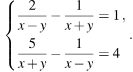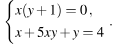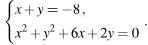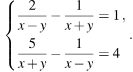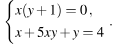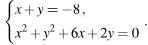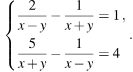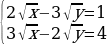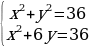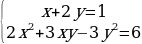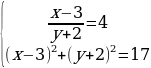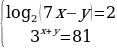Системы и совокупности целых, рациональных, иррациональных, показательных, логарифмических уравнений и неравенств

Дата 06.03.2025

Класс 11

Предмет: алгебра и начала математического анализа

Системы и совокупности целых, рациональных, иррациональных, показательных, логарифмических уравнений и неравенств

Номер урока 72

Тип урока: комбинированный

Планируемые результаты:

Предметные: обобщить умения решать системы уравнений разными способами, уметь решать комбинированные задачи с использованием алгоритмов решения систем уравнений.

Личностные: воспитание чувств ответственности за свои поступки; формирование учебной мотивации и способности к волевому усилию; развитие интереса к изучаемой дисциплине; формирование волевых качеств, коммуникабельности, объективной оценки своих достижений, ответственности.

Метапредметные: воспитание навыков контроля и самоконтроля, развитие коммуникативных навыков при работе в парах

Ход урока.

1. Мотивационный этап. Проверка готовности к уроку.

2. Устная работа (СЛАЙД 1,2)

Что мы сейчас повторили?

-Свойства степеней

-свойства арифметического квадратного корня

-свойства логарифмов

-решение показательных уравнений, его свойства

-решение квадратных уравнений полных и неполных

-решение простейших логарифмических уравнений.

3. Введение в тему урока. Постановка целей и задач.

СЛАЙД 3

СЛАЙД 4

Солнечная система и система уравнений

СЛАЙД

-Солнечная система, в математике есть системы уравнений. А какие еще системы вы знаете?

(Система знаний, система управления,система отсчета…)

Означает это слово?

Систе́ма (древне-греческое σύστημα «целое, составленное из частей; соединение») — множество элементов, находящихся в отношениях и связях друг с другом, которое образует определённую целостность, единство.

Потребность в использовании термина «система» возникает в тех случаях, когда нужно подчеркнуть, что что-то является большим, сложным, не полностью сразу понятным, при этом целым, единым.

Так о чем сегодня будем говорить ?

Записываем тему урока «Системы и совокупности целых, рациональных, иррациональных, показательных, логарифмических уравнений и неравенств»

Какую цель ставим на сегодняшний урок?:( Повторить, что такое система уравнений, методы ее решения)

3.Основной этап.Работа с темой урока

1)Определение системы уравнений СЛАЙД 5 Записывают

Ответьте на вопрос: СЛАЙД 6

1)Что называется решением системы уравнений?

Пару значений (х;у), которая одновременно является решением первого и второго уравнений системы , называют решением системы уравнений.

2)Что значит решить систему уравнений?

Решить систему уравнений - значит найти все ее решения или установить, что решений нет

Что бы решить систему, необходимо определить метод решения.

Какие методы вы изучали ранее? (Называют и записывают)

СЛАЙД

1. СЛАЙД 10. Метод подстановки

2. Выразить из какого-нибудь уравнения системы одну переменную через другую.

3. Подставить в другое уравнение системы вместо этой переменной полученное выражение.

4. Решить получившееся уравнение с одной переменной.

5. Найти соответствующее значение второй переменной.

6. Записать ответ в виде пары чисел (х;у)

1. СЛАЙД 11. Метод сложения

2. Умножьте почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.

3. Сложите почленно левые и правые части уравнений системы.

4. Решите получившееся уравнение с одной переменной.

5. Найдите соответствующее значение второй переменной

6. Записать ответ в виде пары чисел (х;у)

СЛАЙД 12 . Графический метод

1. Построить график функции, заданной первым уравнением системы.

2. Построить график функции, заданной вторым уравнением системы.

3. Определить координаты точек пересечения графиков функций

Записать ответ в виде пары чисел (х;у)

СЛАЙД 13. Метод введения новой переменной

1. Ввести одну или две новые переменные.

2.  Записать новое уравнение или систему уравнений.

3. Решить новое уравнение или систему уравнений и найти значения введённых переменных.

4. Сделать обратную замену и найти значения переменных из условия.

5. Записать ответ.

СЛАЙД 14 . Все методы

Метод подстановки

Метод сложения

Графический метод

Метод введения новой переменной

СЛАЙД 14,15. ВНИМАНИЕ! При решении систем уравнений, мы практически в полной мере руководствуемся теми же принципами, что и при решении обычных уравнений.

Постепенно переходим к более простым уравнениям, выполняя равносильные преобразования.

К уравнениям следствиям мы так же можем переходить, но стоит не забывать, что в этом случае мы должны проверить все полученные корни.

Определение. Две системы уравнений называются равносильными, если они имеют одни и те же решения или если решений нет у каждой из систем.

Определение. Две системы уравнений называются равносильными, если они имеют одни и те же решения или если решений нет у каждой из систем.

Равносильными являются методы:

1. Метод подстановки.

2. Метод сложения.

3. Метод введения новой переменой.

Используя эти методы, мы заменяем исходную систему уравнений равносильной системой, но как правило получившуюся систему решить гораздо проще.

Методы, приводящие к уравнениям следствиям:

1. Возведение в квадрат обеих частей уравнения.

2. Умножение уравнений системы.

3. Преобразования, расширяющие область допустимых значений каждого уравнения.

При использовании данных методов, проверку корней следует проводить всегда!

ФИЗКУЛЬТМИНУТКА

ЗАКРЕПЛЕНИЕ

Работа у доски( карточки)

А) метод подстановки
б) метод сложения
в) метод введения новой переменной
г) графический метод

Перед вами методы решения и системы уравнений . Вам необходимо у каждого метода поставить номер той системы, при решении которой будем применять этот метод.Думаем, проверка по эталону. Слайд 17.

Проверяем ошибки. У кого все верно?

4.Итог урока…Какова была тема урока? Какие цели ставили? Достигли их?Что не получилось?Что давалось с трудом?

Это надо знать

Соотношение количества систем, решаемых различными методами

5.Рефлекия:

ДОМАШНЕЕ ЗАДАНИЕ: