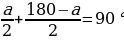Тема. Смежные и вертикальные углы
Цель.
Обучающая:
ввести понятия смежных и вертикальных углов, рассмотреть их свойства;
закрепить умения и навыки учащихся использовать свойства смежных и вертикальных углов при решении задач, использовать их в нестандартных ситуациях;
научиться применять на практике свойства смежных и вертикальных углов с доказательствами;
строить угол, смежный с данным углом, изображать вертикальные углы, находить на рисунке смежные и вертикальные углы, решать простейшие задачи по теме.
Развивающая:
развивать творческую и мыслительную деятельность, логическое мышление учащихся в процессе изучения нового материала и решения задач;
развивать познавательный интерес и любознательность учащихся, умения самостоятельно работать, излагать мысли грамотным математическим языком.
Воспитательная:
прививать учащимся интерес к предмету;
формировать умения аккуратно и грамотно выполнять математические записи и чертежи;
учить умению сосредотачиваться на учебной деятельности и предупреждать ошибки по невнимательности.
Планируемые результаты:
Предметные УУД:
- формировать умение понимания, какие углы называются смежными, какие – вертикальными;
- формировать умение формулировать и обосновывать утверждения о свойствах смежных и вертикальных углов;
- формировать умение решать задачи: вычисление градусной меры угла, смежного с данным одним действием, с помощью уравнения; вычисление градусной меры угла, вертикального с данным углом.
| Знания | Умения |
| Смежные углы | Строить угол, смежный с данным углом |
| Свойство смежных углов | Определять градусную меру угла, смежного с данным |
| Каждая пара смежных углов составляет один развёрнутый угол |
|
| Вертикальные углы | Строить вертикальные углы |
| Свойство вертикальных углов | Находить вертикальные углы |
Эвристический приём: моделирование
Задача
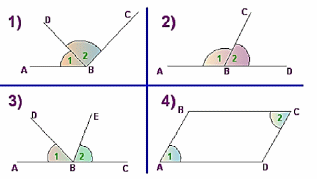
Учитель предлагает учащимся объяснить, почему на рисунках 3 и 4 углы не могут быть смежными?
(на рисунке 3 у углов 1) и 2) нет общей стороны, на рисунке 4 углы 1) и 2) по определению не являются смежными)
Задача
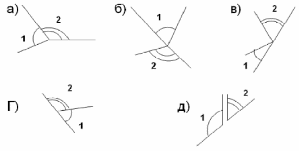
Учащиеся без помощи учителя должны определить, на каком из рисунков углы 1 и 2 смежные, а на каких рисунках – нет. Учащиеся объясняют свой выбор, используя теоретический материал темы.
(Смежными углы являются под ответом Г. В остальных случаях углы 1) и 2) не являются смежными по определению)
Задача
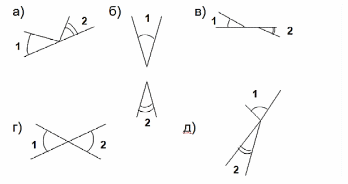
Учащиеся без помощи учителя должны определить, на каком из рисунков углы 1 и 2 вертикальные, а на каких рисунках – нет.
(углы 1) и 2) являются вертикальными только в ответе Г, так как в остальных случаях они таковыми не являются по определению.
Как уравнения помогают решать геометрические задач?
Задача.


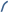
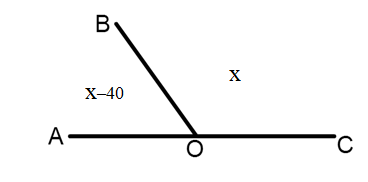
Учитель предлагает учащимся составить задачу по рисунку, в которой требовалось бы найти величины смежных углов, составив уравнение. При составлении уравнения учащиеся объясняют, каким свойством смежных углов они воспользовались. Учащиеся рассуждают так: пусть один угол равен х, другой х–40. Зная, что сумма смежных углов равна 180°, составим уравнение: х+х–40=180. Решить это уравнение детям будет несложно. х – первый искомый угол, х–40 – второй искомый угол.
Задача
Составьте задачу на нахождение величин смежных углов, которая бы сводилась к решению уравнения х+5х=180.
Даная задача для учащихся несложная. Учащиеся могут составить задачу следующим образом: из точки О, лежащей на прямой АС, луч ОВ отсекает от этой прямой два угла. Один из них в пять раз больше другого. Необходимо найти эти углы. Учащимся нетрудно будет по уравнению составить и решить задачу, пользуясь свойством смежных углов.
Данный эвристический метод применяется на этапе только изученного нового материала по данной теме, на этапе первичного закрепления полученных новых знаний. Учащиеся могут ещё допускать ошибки, поэтому данные задачи целесообразно применять как эвристический приём Моделирование.
Эвристический приём: метод малых изменений
Задача
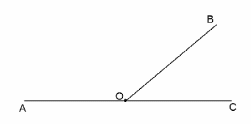
Учитель предлагает учащимся решить следующую задачу по данному рисунку: пусть ∠АОВ и ∠СОВ – смежные углы. Пусть ∠АОВ измеряется в границах от 0° до 60°. В каких границах измеряется при этом ∠СОВ?
(Возможно рассуждение учащихся: Сумма смежных углов равна 180°. Так как если один из смежных углов измеряется от 0° до 60°, то второй тогда измеряется 180°–60°=120° и 180°–0°=180°. Значит, второй из смежных углов измеряется от 120° до 180°.
Эвристический приём: обобщение
При объяснении нового материала по теме «Смежные и вертикальные углы» после введения понятия смежных углов учитель предлагает учащимся выполнить лабораторную работу на открытие свойства смежных и вертикальных углов.
Тема лабораторной работы: «Свойства смежных и вертикальных углов»
Цель. Выяснить, какие свойства имеют смежные и вертикальные углы.
Оборудование:
Ход работы
1. Построй угол b смежный углу а, если а: острый, прямой, тупой.
2. Измерь величины углов.
3. Данные измерений занеси в таблицу.
4. Найди соотношение между величинами углов а и b.
5. Сделай вывод о свойстве смежных углов.
| № опыта | Величина угла а | Величина угла b |
| 1 | Острый | |
| 2 | Прямой | |
| 3 | Тупой | |
5. Построй угол b смежный углу а, если а: острый, прямой, тупой.
6. Измерь величины углов.
7. Данные измерений занеси в таблицу.
8. Найди соотношение между величинами углов а и b.
9. Сделай вывод о свойстве смежных углов.
| № опыта | Величина угла а | Величина угла 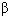 |
| 1 | Острый | |
| 2 | Прямой | |
| 3 | Тупой |
|
Вывод. Учащиеся записываю его самостоятельно:
Свойство смежных углов __________________________________________
Свойство вертикальных углов ___________________________________
Эвристический приём: доказательство от «противного»
При закреплении изученного материала по данной теме, при обобщении теоретического материала, учащимся можно предложить решить следующую задачу: Если сумма двух углов равна 170°, то они смежные.
Учащиеся при решении данной задачи может использовать приём доказательство «от противного». Ход доказательства: Пусть смежные углы в сумме дают 170°. По определению смежные углы – это углы, у которых одна сторона общая, а две другие лежат на одной прямой. Если сумма смежных углов равна 170°, то между двумя несовпадающими сторонами смежных углов будет 170°, а значит между ними тупой угол. А по определению угол должен быть развёрнутым и составлять 180°. Пришли к противоречию. Значит, если сумма двух углов равна 170°, то они не смежные.
Эвристический приём: контрпример и подтверждающий пример
Учитель предлагает доказать или опровергнуть обратное утверждение к равенству вертикальных углов: «Верно ли, что если углы равны, то они вертикальные»?
Ход рассуждения: «Равные углы могут быть и не вертикальными. Они могут быть, например, смежными (90° и 90°), накрест лежащими. Поэтому теорема, обратная к теореме о равенстве вертикальных углов, не верна. Взаимное расположение углов может быть различным.
Эвристические приёмы обобщение, доказательство «от противного», контрпример лучше применять на этапе систематизации, обобщения материала. Данные задачи следует рекомендовать для работы в группах.
Эвристический приём: анализ задачи
Этот приём лучше всего применять тогда, когда учащиеся хорошо уже овладели теоретическим материалом по теме «Смежные и вертикальные углы», решили достаточное количество задач по этой теме. Учитель предлагает учащимся решить следующую задачу: «Найдите угол между биссектрисами смежных углов».


p l

n

k m
Ход рассуждений учащихся: «Пусть ∠ml и ∠kl – смежные (по условию). Обозначим ∠ml=а, тогда ∠kl=180 – а. Проведём биссектрисы этих углов. Из определения биссектрисы имеем ∠nl=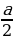 , a ∠pl=
, a ∠pl=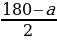 . ∠pn=∠nl+∠pl=
. ∠pn=∠nl+∠pl=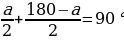
Эвристический приём: разбиение целого на части
Задача
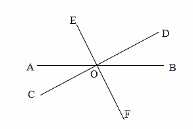
Учащимся учитель предлагает решить следующую задачу: «Через точку проведены три прямые. Величины скольких углов нужно задать, чтобы можно было найти величины остальных углов?»
Если данная задача вызывает у учащихся затруднение, то учитель может предложить детям сначала выбрать любой угол и задать его величину. Например, выберем ∠АОС=30°. Далее, учитель предлагает рассмотреть ∠DOB. Задание учащимся: оцените эти углы. Учащиеся по определению вертикальных углов обозначают, что ∠АОС и ∠DOB – вертикальные. Значит, нецелесообразно задавать величину второго вертикального угла, зная величину первого. Рассуждаем далее: зададим величину ∠COF=80°. Далее учащиеся могут определить, что ∠EOD=80° по определению вертикальных углов. Далее учащиеся должны рассуждать: ∠АOF=∠АОС+∠COF=30°+80°=110°. По определению смежных углов ∠АOF и ∠АOЕ – смежные. Как найти один из смежных углов, зная другой, учащиеся знают. Найдя ∠АOЕ, детям будет нетрудно найти и ∠BOF. Значит, для нахождения всех углов, обозначенных на рисунке, достаточно задать величины ∠АОС и ∠COF.
Данный эвристический приём целесообразно применить на этапе систематизации и обобщения знаний учащихся, при подведении итогов урока, на этапе рефлексии.
Подведение итогов урока












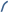
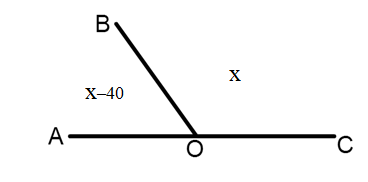





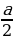 , a ∠pl=
, a ∠pl=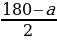 . ∠pn=∠nl+∠pl=
. ∠pn=∠nl+∠pl=