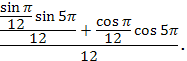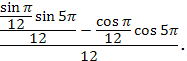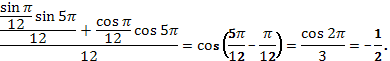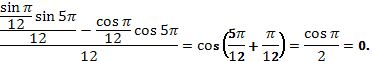"Способы решения тригонометрических уравнений. Итоговый урок"
Цели урока:
Образовательные:
повторить способы решения некоторых видов тригонометрических уравнений;
систематизировать полученные знания, активизировать самоконтроль, взаимоконтроль.
Развивающие:
Воспитательная:
Тип урока: итоговый урок
Формы работы учащихся: фронтальная, индивидуальная
Необходимое оборудование: карточки с устными и подготовительными упражнениями, 4 варианта самостоятельной работы.
Ход урока
Организационный момент.
Устные упражнения.
Подготовительные упражнения.
Повторение методов решения тригонометрических уравнений.
Самостоятельная работа.
Подведение итогов урока.
Домашнее задание.
Организационный момент.
Приветствие учителя, отметить отсутствующих, проверить подготовку к уроку. Сообщить тему и цель урока.
Устные упражнения.
Что называется арксинусом, арккосинусом, арктангенсом числа? Привести примеры.
Для каких чисел определен арксинус, арккосинус, арктангенс.
Написать формулы нахождения корней уравнений: sin x = a, cos x = a, tg x = a.
Формулы:
sinx =+/-- a x = 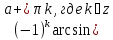
sinx = 0 x = 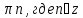
sinx = 1 x =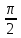 +
+ 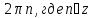
sinx = -1 x = -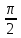 +
+ 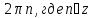
cosx = +/- a x = ± arccos a + 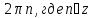
cosx = 0 x =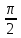 +
+ 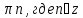
cosx = 1 x = 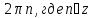
cosx = -1 x = 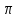 +
+ 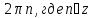
tgx =+/- a x = arctg a + 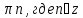
ctgx = +/-a x = arcctg a + 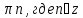
При каких значениях а уравнения sin x = a, cos x = a, tq x = a имеют решения?
Вычислить: Решить простейшиеЛюбой метод решения тригонометрических уравнений состоит в том, чтобы привести их к простейшим, то есть к уравнениям вида sinx = a, cosx =а, tgx = a, ctgx = a. Простейшие тригонометрические уравнения учащиеся умеют решать. Другие являются специфическими именно для тригонометрии.
уравнения: 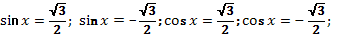
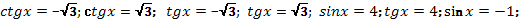
ctg x=0; cos x=1
Подготовительные упражнения.
Пользуясь формулами сложения преобразовать выражения:
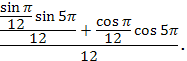
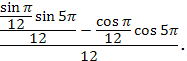
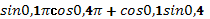 .
.
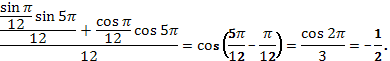
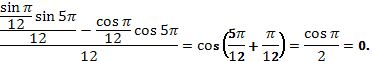
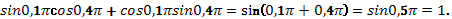
Повторение методов решения тригонометрических уравнений.Чтобы успешно решать простейшие тригонометрические уравнения необходимо следующее:
уметь отмечать точки на числовой окружности;
уметь определять значения синуса, косинуса, тангенса и котангенса для точек числовой окружности;
знать свойства основных тригонометрических функций;
знать понятия арксинуса, арккосинуса, арктангенса и арккотангенса и уметь отмечать их на числовой окружности.
Некоторые из методов (например, замена переменной или разложение на множители) являются универсальными, то есть применяются и в других разделах математики.
Замена переменной и сведение к квадратному уравнению
Это универсальный способ. Применяется в любых уравнениях: степенных, показательных, тригонометрических, логарифмических, каких угодно. Замена не всегда видна сразу, и уравнение нужно сначала преобразовать.
Метод сведения к квадратному состоит в том, что, пользуясь изученными формулами, надо преобразовать уравнение к такому виду, чтобы какую-то функцию (например, sinx или cosx) или комбинацию функций обозначить через y, получив при этом квадратное уравнение относительно y.
Решение методом введения новой переменной.
4sin2x+11sinx – 3 =0.
Введём новую переменную: t=sin x, t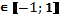 приходим к квадратному уравнению:
приходим к квадратному уравнению:
4t2+11t – 3=0.
Корни данного уравнения t1= -3; t2=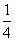 .
.
Делаем обратную замену с учетом, что t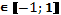 sin x=
sin x=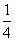 . Решаем данное уравнение:
. Решаем данное уравнение:
x = arcsin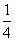 + 2
+ 2 .
.
x =  .
.
Ответ можно записать в следующем виде:
a) x =  .
.
5sin2x+6cos x – 1 =0.
Из основного тригонометрического тождества sin2x=1 – cos2x, следовательно исходное уравнение примет вид: -5cos2x+6cos x – 1=0.
Введём новую переменную t=cos x, t
 . Приходим к квадратному уравнению:
. Приходим к квадратному уравнению:
-5t2+6t – 1=0. Корни данного уравнения t1=1; t2=  . Оба корня подходят. Делаем обратную замену.
. Оба корня подходят. Делаем обратную замену.
cos x=1
Частный случай х= .
.
cos x= .
.

 .
.
Однородные тригонометрические уравнения
Уравнение вида аsinx + bcosx = 0 называют однородным тригонометрическим уравнением первой степени.
5 sinx - 2 cosx = 0 ответ:x = arctg +
+ ,
, 
Алгоритм решения однородного тригонометрического уравнения первой степени:
Уравнение вида аsinmx + bcosmx = 0тоже называют однородным тригонометрическим уравнение первой степени и решают также делением обеих частей уравнения на косинус mх.
Уравнение видаa sin2x + b sinxcosx + c  = 0называют однородным тригонометрическим уравнением второй степени.
= 0называют однородным тригонометрическим уравнением второй степени.
Их решение начинается с того, что обе части уравнения делятся на cos2x (или на sin2 x).
Решение однородного уравнения.
cos2x+4sin2x=2sin2x.
Перепишем уравнение с учётом формулы двойного угла cos2x+4sin2x=4sin xcos x. Разделим обе части уравнения на cos2x Получим уравнение 4tg2x-4tg2x+1=0. Введём новую переменную: t=tgx, уравнение примет вид 4t2 – 4t+1=0. Корень данного уравнения: t= 0,5. Сделаем обратную замену tg x=0,5. Ответ: х = arctg.
Получим уравнение 4tg2x-4tg2x+1=0. Введём новую переменную: t=tgx, уравнение примет вид 4t2 – 4t+1=0. Корень данного уравнения: t= 0,5. Сделаем обратную замену tg x=0,5. Ответ: х = arctg.
Алгоритм решения однородного тригонометрического уравнения второй степени:
Посмотреть, есть ли в уравнении член asin2x.
Если член asin2x в уравнении содержится (т.е. а  0), то уравнение решается делением обеих частей уравнения на cos2x и последующим введение новой переменной.
0), то уравнение решается делением обеих частей уравнения на cos2x и последующим введение новой переменной.
Если член asin2x в уравнении не содержится (т.е. а = 0), то уравнение решается методом разложения на множители: за скобки выносят cosx.
Однородные уравнения вида asin2mx + bsinmxcosmx + c cos2mx = 0решаются таким же способом.
Введение дополнительного угла
Этот метод применяется для уравнений a cosx + bsinx = c. Он присутствует в школьных учебниках. Правда, в них рассматриваются только частные случаи – когда числа a и b являются значениями синуса и косинуса углов 30º, 45º или 60º.
Введение вспомогательного угла.
sin x+7cos x=5.
Решим методом вспомогательного угла. Найдём  Разделим обе части на
Разделим обе части на  , получим
, получим  . sin
. sin  , cos
, cos . Тогда tg
. Тогда tg  =7 и
=7 и  =arctg7. Применим формулу синуса суммы, получим:
=arctg7. Применим формулу синуса суммы, получим:
sin(x+ )=
)= , отсюда x+
, отсюда x+ =
=
x=
Ответ:  arctg7.
arctg7.

Разделим обе части на 2, получим 
 Уравнение примет вид
Уравнение примет вид  Применим формулу синуса разности получим: sin(x -
Применим формулу синуса разности получим: sin(x -  )=
)= . (x -
. (x -  )=. Ответ: x=
)=. Ответ: x= Ответ можно записать в следующем виде: х=
Ответ можно записать в следующем виде: х=
Разложение на множители
Под разложением на множители понимается представление данного выражения в виде произведения нескольких множителей. Если в одной части уравнения стоит несколько множителей, а в другой – 0, то каждый множитель приравнивается к нулю. Таким образом, данный множитель можно представить в виде совокупности более простых уравнений.
Разложение на множители.
sin2x – sin x=0.
Вынесем sin x за скобки, получим уравнение: sin x(sin x – 1) = 0; sin x=0 или sin x – 1 =0.
Ответ:x= n , n
n , n Z. x=
Z. x=
Решение уравнений с применением формул
Преобразование суммы тригонометрических функций в произведение
Пример sinx + sin (x +  ) = 0
) = 0
Применив формулу, получим равносильное уравнение
2sin (x + )cos
)cos = 0
= 0
Ответ: x = - 
Преобразованием произведения тригонометрических функций в сумму
Пример cos3x + sinxsin2x = 0
Применив формулу, получим уравнение
cos3x +  cosx -
cosx - 
 +
+  cosx = 0
cosx = 0
cos2xcosx = 0
Ответ:x =  +
+  x =
x =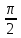 +
+ 
При решении широкого круга тригонометрических уравнений ключевую роль играют формулы понижения степени.
Решение уравнений с применением формул понижения степени
Пример 1 +
+ -
-  -
-  = 0
= 0
Применив формулу, получим уравнение
 +
+  –
–  –
–  = 0
= 0
(cos8x – cos2x) + (cos6x – cos4x) = 0
-2sin3xsin5x – 2sinxsin5x = 0
-2sin5x(sin3x + sinx) = 0
-4sin5xsin2xcosx = 0
Ответ: x =  ,
, +
+ 
Применение различных формул.
Применяем формулу синуса разности.
sin 4x cos2x – cos4x sin2x=0.
Подобный пример уже рассматривался.
Группирование:
3sin2x – 4cosx + 3sinx – 2=0.
Решение: 6sin x cosx+3sinx – 4cosx – 2=0,
3sinx(2cosx+1) – 2(2cosx+1)=0.
(2cosx+1)(3sinx – 2)=0.
2cosx+1=0 или 3sinx – 2=0.
cos x= , x=
, x=
sin x= , x=
, x=  .
.
Ответ:
Самостоятельная работа (10 – 15 мин.).
| 1 Вариант. cos2x – 3cos x=sin2x+4. sin x+ cos x=0. cos x=0. sin2x – sin x=0. | 2 Вариант. sin3x+sin x=sin2x. 2cos2x+5sin x – 4=0. sin x – cos x=1. |
| 3 Вариант. 2sin2x – 7sin x+3=0. 3sin x – cos x=1. sin3x cos5x=cos3x sin5x. | 4 Вариант. sin x +7cos x=5. sin2x – sin x cos x – 2cos2x=0. cos x+cos2x+cos3x=0. |
Подведение итогов урока.
Данный урок последний перед контрольной работой по теме: “ Решение тригонометрических уравнений”. На уроке рассмотрены основные методы решений тригонометрических уравнений, разбираемые в школе.
Формула дополнительного угла
Любое выражение вида asinα+bcosα можно представить в виде
Asin(α+ϕ)
Для этого вынесем за скобки выражение √a2+b2:asinα+bcosα=√a2+b2(a/√a2+b2⋅sinα+b/√a2+b2⋅cosα)
Но (a/√a2+b2)2+(b/√a2+b2)2=1
Это значит, что точка с координатами a/√a2+b2 и b/√a2+b2 удовлетворяет уравнению x2 + y2 = 1, т.е. лежит на числовой окружности.
Поэтому существует такое ϕ, что a/√a2+b2=cosϕ,b/√a2+b2=sinϕ
Обозначим √a2+b2 через A, получим asinα+bcosα=A(cosϕ⋅sinα+sinϕ⋅cosα)=Asin(α+ϕ)
Итак, формула дополнительного угла:
Обобщающий урок с элементами тренинга по теме:“Решение тригонометрических уравнений”.
Цели:
Обучающие:
1. Обобщить и систематизировать материал по данной теме.
2. Провести контроль за уровнем сформированности знаний,
умений и навыков.
Развивающие:
3. Продолжить формирование навыков коммуникативной работы.
4. Развивать логическое мышление, умение сравнивать, находить
общие черты и различия.
Воспитывающие:
5. Воспитывать чувство коллективизма, взаимопомощи,
отзывчивости, работоспособности.
Тип урока: Урок обобщения и систематизации знаний.
Форма: Урок-тренинг.
Методы: 1. Метод неоконченных тезисов.
2. Тренинги.
3. Групповая работа.
4. Само и взаимоконтроль.
5. Самооценка.
Оборудование: Тренинг “Третий лишний”, тренинг-выбор
по теме, интерактивная доска.
Ход урока.
Приветствие ребят.
Организационный момент.
Сегодня у нас заключительный урок по теме: «Решение тригонометрических уравнений». Повторяем, обобщаем, приводим в систему изученные виды, типы, методы и приемы решения тригонометрических уравнений.
Перед нами стоит задача – показать свои знания и умения по решению тригонометрических уравнений.
Проверочная работа.
Цель: контроль знаний и приведение в систему знаний по простейшим
тригонометрическим уравнениям.
Метод неоконченных тезисов (Я начинаю – вы продолжаете).
I вариант II вариант
1) Arcsin a находится 1) Arccos a находится
в промежутке…. в промежутке….
2) Arcctg a находится 2) Arctg a находится
в промежутке…. в промежутке….
3) Уравнение cosx = a имеет 3) Уравнение sinx = a имеет
решение при …. решение при ….
4) Какой формулой выражается 4) Какой формулой выражается
это решение? это решение?
5) Cosx = 1 при …. 5) Sinx = 1 при ….
6) Sinx = -1 при …. 6) Cosx = -1 при ….
7) Cosx = 0 при …. 7) Sinx = 0 при ….
8) Уравнение tgx = a имеет 8) Уравнение ctgx = a имеет
решение при …. решение при ….
9) Какой формулой выражается 9) Какой формулой выражается
это решение …. это решение ….
Собираем работы.
Ответы на интерактивной доске (самопроверка)
I вариант II вариант
1) [- ] 1) [0; π]
] 1) [0; π]
2) (0; π) 2) (- )
)
3) ׀a׀ ≤ 1 3) ׀a׀ ≤ 1
4) ±arccos a + 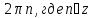 4)
4)  arcsin a + πk, где
arcsin a + πk, где 
5) x = 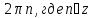 5)
5) 
6) -  6) π +
6) π + 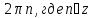
7)  7)
7) 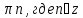
8) a - любое 8) a – любое
9) arctg a + 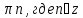 9) arcctg a +
9) arcctg a + 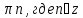
Тренинг “Третий лишний” (на интерактивной доске).
1. Даны три уравнения, два из которых обладают общим способом решения
а) 2
b) 2
c) 5 - 2
Укажите, что за способ. Какое уравнение лишнее?
Ответ: лишнее b. Уравнения a и c – квадратные.
2. Даны три уравнения
a) 
b) 
c) 
Укажите, что за способ. Какое уравнение лишнее?
Ответ: лишнее c. Уравнения a и b – однородные.
Тренинг-выбор (группа – 4человека)
Оценочный лист
| Ф.И.О. класс № стола |
| № задания | Ваш выбор | Выбор после общения с партнером | Выбор после общения в кластере | Балл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ТРЕНИНГ-ВЫБОР
I этап. Индивидуальный
Задание: Из перечисленных ниже вариантов ответов на вопросы и задачи
выберите правильный. И запишите его в соответствующую
клеточку графы “Ваш выбор”.
Задания:
Решите уравнение 4 - 
а)  б) в)
б) в)  г)
г)  arcsin3+ πk, где
arcsin3+ πk, где  и
и 
2. Предложите способ решения данного тригонометрического уравнения:
1 – приведение к квадратному уравнению;
2 – приведение к однородному уравнению;
3 – приведение к уравнению относительно тангенса;
4 – разложение на множители
5 – с помощью формул
а)  = 1-
= 1-  cosx
cosx
б) 3sinx + 5 cosx = 2
в) 
г) sinx + sin2x + sin3x = 0
д) 
а – б – в – г – д –
3. Решите уравнение
а) arctg ( ) + πk, где
) + πk, где  и
и 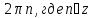 б)
б) 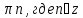
в) -arctg  + πk, где
+ πk, где  г)
г) 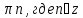 и -arctg
и -arctg  + πk, где
+ πk, где 
4. Решите уравнение на указанном промежутке
cosx +  = 0 на (π;
= 0 на (π;  π)
π)
а) ± π +
π +
 б)
б)  π в) ± г)
π в) ± г) π
π
5. Решите уравнение tgx – 2sinx = 0
а) ± б) ± в) г) ±
г) ±
6. Решите уравнение sinx + cosx = 
а)  +
+  б)
б)  +
+  в)
в) +
+  г) arctg(
г) arctg( ) +
) + 
IV этап. Подведение итогов.
Каждый правильный ответ – 1 балл.
Оценочные листы сдаются.
Правильные ответы на интерактивной доске:
Задание №1 – в
Задание №2 – а) 4 и 2, б) 3, в) 5, г) 5 и 4, д) 1
Задание №3 – г
Задание №4 – б
Задание №5 – а
Задание №6 - б
11 – 12 баллов – “5”
8 – 9 баллов – “4”
6 – 7 баллов – “3”
Домашнее задание с сайта «Решу ЕГЭ» - на выбор 5 заданий.







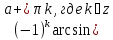
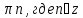
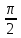 +
+ 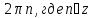
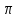 +
+