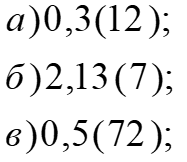9-В класс Алгебра 28.11.2022 учитель Кузьмин В. А
Тема: Сравнение действительных чисел
Цель:
обучающая
Формирование, подтверждение и проверка теоретических знаний по делению, используя правила приближенного округления; выполнение действий с точностью до 0,000001, используя округление.
развивающая
Развивать логическое мышление; умение анализировать, обобщать, делать выводы; умение работать в должном темпе.
воспитывающая
Воспитывать самоконтроль; самостоятельность при выполнении действий и оформлении результатов.
Ход урока
Организационный момент
Запись даты и темы урока
Актуализация опорных знаний
Перечислите множества чисел (натуральные, рациональные, иррациональные, действительные).
Какое множество включает все числа? (действительные)
При округлении, когда мы прибавляем «1» к предыдущему числу, когда отбрасываем числа (когда меньше пяти).
При преобразовании бесконечной периодической дроби на что надо обратить внимание? (количество цифр, стоящих перед периодом после запятой и количество цифр, стоящих в периоде)
Теоретическая часть
Изучение математики начинается с натуральных чисел, т.е. с чисел 1, 2, 3, 4, 5,… . При сложении и умножении натуральных чисел всегда получаются натуральные числа. Однако разность и частное натуральных чисел могут не быть натуральными числами.
Дополнением натуральных чисел нулем и отрицательными числами (т.е. числами, противоположными натуральным) множество натуральных чисел расширяется до множества целых чисел, т.е. чисел 0, ± 1, ± 2, ± 3, … . При сложении, вычитании и умножении целых чисел всегда получаются целые числа. Однако частное двух целых чисел может не быть целым числом.
При выполнении четырех арифметических действий (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа.
Бесконечную десятичную дробь 0,3333… называют периодической, повторяющуюся цифру 3 – ее периодом. Периодическую дробь 0,333… коротко записывают так: 0,(3); читается: «Ноль целых и три в периоде».
Периодическая дробь – это бесконечная десятичная дробь, у которой начиная с некоторого десятичного знака повторяется одна и та же цифра или несколько цифр – период дроби.
Если бесконечная десятичная дробь непериодическая, то она не является рациональным числом. Например, дробь 0,101001000100001…, в которой после первой цифры 1 стоит один нуль, после второй цифры 1 – два нуля и, вообще, после n – й цифры стоит n нулей, не является периодической. Поэтому написанная дробь не представляет никакого рационального числа. В этом случае говорят, что данная дробь является иррациональным числом.
Иррациональным числом называется бесконечная десятичная непериодическая дробь.
Практическая часть (выполните задания письменно)
Задание 1. Представить в виде бесконечной десятичной дроби числа. Выполнить деление столбиком, не используя калькулятор.
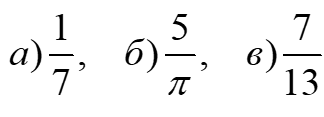
Решение:
 а) 10 7
а) 10 7
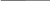

 7 0, 1428571…
7 0, 1428571…
30





 28
28
20



 14
14
60
56
40
35
50
49
10
7 и т.д.
Задание 2. Преобразовать бесконечную периодическую дробь в обыкновенную:
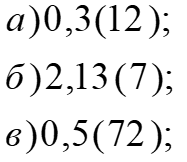
Решение:
а) Пусть х=0,31212…(*10
10х=3,12…(*100
1000х=312,12…
1000х-10х=312,12…-3,12…
990х=309
х=309/990=103/330
Задание 3. Выполнить действия. Найти сумму и произведение чисел:
а) х = 3, 5151151115..; б) х = 2,36…;
у = 4,343343334... у = 1,020020002.
Решение
Если дроби имеют много знаков после запятой, выполнить эти действия быстро довольно сложно. Для этого используют правила приближения суммы, разности, произведения и частного двух чисел.
Сумма (разность, произведение, частное) двух чисел считается приближённо равной сумме (разности, произведению, частному) их приближений.
а) х+у= 3,5151151115…+ 4,343343334…
Округлим данные числа до сотых.
3,5151151115…≈ 3,52
4,343343334…≈ 4,34
Сложим приближённые значения дробей.
3,52+4,34=7,86
х+у= 3,5151151115…+ 4,343343334…≈ 7,86
Итак, чтобы вычислить приближённую сумму или разность двух чисел, надо округлить эти числа с одинаковой точностью, то есть до одного и того же разряда. Затем сложить или вычесть полученные приближения.
Чтобы вычислить приближённое произведение или частное двух чисел, надо округлить эти числа с точностью до одной и той же значащей цифры, перемножить или разделить полученные приближения и результат округлить до той же значащей цифры.
х*у= 3,5151151115…* 4,343343334…
Найдём их произведение.
Округлим числа до трёх значащих цифр.
3,5151151115…≈ 3,52
4,343343334…≈ 4,34
Вычислим произведение их приближений.
3,52*4,34=15,2768
Округлим результат также до трёх значащих цифр.
15,2768 ≈ 15,3
Получаем, что
х*у= 3,5151151115…* 4,343343334…≈ 15,3
Точность вычислений находится в противоречии с простотой вычислений. Чем большим количеством цифр мы пользуемся, тем точнее наш результат.
Контрольные вопросы и задания
Ответить на вопросы:
Может ли сумма двух рациональных чисел быть иррациональным числом? (нет)
Сумма двух иррациональных чисел может быть рациональным числом? (да)
Домашнее задание: Повторить теоретическую часть






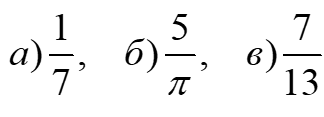
 а) 10 7
а) 10 7