ПРИМЕНЕНИЕ ТЕХНИКИ «ОРИГАМИ» ДЛЯ ИЗУЧЕНИЯ ГЕОМЕТРИЧЕСКИХ ФИГУР В НАЧАЛЬНОЙ ШКОЛЕ
Петерсон Юлия Дмитриевна, студентка 3 курса
КГБПОУ «Красноярский педагогический колледж №1 им. М. Горького»
Научный руководитель: Баранова Марина Юрьевна
Аннотация статьи. В статье рассматриваются вопросы изучения геометрических фигур и их свойств в начальной школе. Автор предлагает включение техники «оригами», как один из методов получения новых знаний в практической деятельности. В статье продемонстрированы идеи рассматриваемой техники, позволяющие в занимательной форме изучить геометрические фигуры.
Ключевые слова: оригами, геометрические фигуры.
Геометрический материал традиционно является одним из самых сложных разделов при изучении математики в школе. В 1-4 классах темы по геометрии носят, как правило, пропедевтический характер. Также отметим, что в учебном процессе изучение элементов геометрии опирается на практическую деятельность и опору на наглядный материал.
Несмотря на ознакомительный характер заданий, в начальном курсе математики геометрический материал обязан представлять точную систему, которая даст возможность ученику постепенно овладеть образами фигур и их отношений. А уже в курсе основной и старшей школы будет более подробно изучаться понятийный аппарат с опорой на родо-видовые признаки. Иными словами, в начальной школе фактически складывается база геометрических представлений.
Основное содержание геометрического материала, представленного в учебниках начальной школы, позволяет освоить понятие «геометрическая фигура». Оперируя предметами разной формы, моделями геометрических фигур, выполняя над ними большое число наблюдений и действий, ученики фиксируют их общие признаки, на основе которых складываются образы геометрических фигур. Обратим внимание, что все окружающие нас предметы не являются, так называемыми, «чистыми фигурами». То есть в природе нет идеально ровного квадрата, куба и т.д. Но мы можем утверждать, что тот, или иной предмет имеет форму, близкую к квадрату, кругу и т.д.
В примерной программе по математике выделен раздел, предполагающий изучение геометрических фигур. Перечисленные в разделе темы являются обязательными для изучения вне зависимости от учебно-методического комплекта и отражены в виде упражнений во Всероссийской проверочной работе (далее – ВПР).
Проанализировав результаты ВПР по Красноярскому краю за 2021 год [4], делаем вывод о том, что всего 62% обучающихся демонстрируют умение исследовать и распознавать геометрические фигуры.
В чем причина такого показателя? Оторванность геометрии от практической деятельности – основной недостаток преподавания математики в традиционной школе. Это является существенной причиной отчуждения школьников от данного предмета и проявляется в потере их интереса к изучению геометрии.
Возникает вопрос о том, как изучать геометрические фигуры в начальной школе, в частности в 4 классе.
Для ответа на данный вопрос на первом шаге нашего исследования была проанализирована авторская программа «Школа России». Нами выделены следующие предметные результаты блока «Пространственные отношения. Геометрические фигуры»:
описывать взаимное расположение предметов на плоскости и в пространстве;
распознавать, называть, изображать геометрические фигуры (точка, прямая, кривая, отрезок, ломаная, прямой угол; многоугольник, в том числе треугольник, прямоугольник, квадрат; окружность, круг);
выполнять построение геометрических фигур с заданными размерами (отрезок, квадрат, прямоугольник) с помощью линейки, угольника;
использовать свойства прямоугольника и квадрата для решения задач;
распознавать и называть геометрические тела (куб, шар, пирамида);
соотносить реальные объекты с моделями геометрических фигур.
Отметим, что согласно данной программе, обучающиеся знакомятся не только с геометрическими фигурами, но и с геометрическими телами.
Ниже в таблице представлены примеры упражнений учебника для обучающихся 4 класса (табл.1).
Таблица 1. Примеры заданий из учебника
| Геометрические фигуры | Пример задания |
| Шар | 
|
| Пирамида | 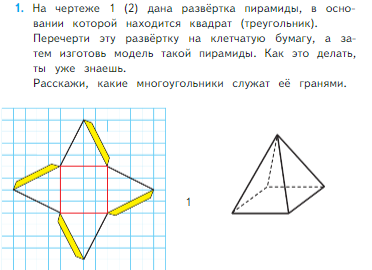
|
| Куб | 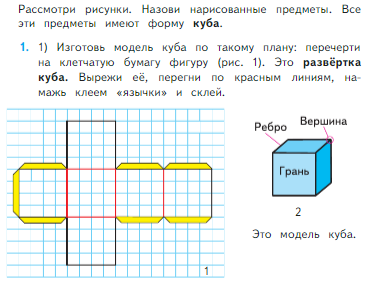
|
Отметим, что изучение всех геометрических тел сопровождается изготовлением модели с помощью бумажной развертки или вспомогательного материала (пластилин, тесто). Такой подход гарантирует более качественное восприятие изученного материала и развитие пространственного воображения.
Одним из механизмов развития геометрического мышления и поддержания интереса к геометрии может стать совместное изучение геометрии совместно и техникой оригами, а именно работа с ее базовыми моделями. Многие учителя математики отмечают, что оригами - мир геометрических фигур: треугольников, квадратов, многоугольников.
Раскроем идею данной техники. Оригами - японское искусство складывания из бумаги фигурок людей, животных, геометрических тел. Искусство, которое вводит нас в мир трехмерного пространства. Оно возникло много веков назад в Японии и распространилось по всему миру.
В переводе с японского языка «оригами» значит «сложенная бумага». В рамках данной техники можно использовать как один квадратный или прямоугольный лист, так и несколько одинаковых. В таком случае мы имеем дело с так называемым «модульным» оригами. Именно поэтому в Японии искусство оригами называют искусством целого листа. Главная особенность оригами, способствующая его быстрому распространению - практически неограниченные возможности, кроющиеся в обычном листе бумаги [1, с.114].
Оригами помогает создать пространственную, наглядную модель любого объекта с помощью заданного алгоритма складывания листа, получая различные геометрические фигуры. А значит, оно дает возможность познакомить обучающихся в процессе изготовления продукта со всеми геометрическими объектами и облегчает усвоение систематического курса геометрии.
Можем утверждать, что изучение возможных превращений квадратного листа бумаги – один из наиболее интересных путей создания образов плоских и пространственных геометрических фигур [2, с.27]. В процессе складывания фигур оригами, обучающиеся знакомятся с различными геометрическими фигурами: треугольником, квадратом, трапецией и т.д., учатся легко ориентироваться в пространстве и на листе бумаги, делить целое на части, находить вертикаль, горизонталь, диагональ.
Именно поэтому на данную технику обратили внимания учителя математики и начальных классов. Американский педагог Ф. Фребель уже в середине XIX века заметил геометрическую особенность оригами и ввел его как учебный предмет в школе. Например, основы геометрии он предлагал изучать не с помощью циркуля, линейки и некоторых понятий, а на примере фигур складывающейся бумаги. Он активно внедрял оригами в педагогический процесс [3, с.16].
Продемонстрируем, как можно с помощью простых базовых форм оригами изучить осевую симметрию в начальной школе. Для этого каждому обучающемуся нужно выдать белый квадратный лист и попросить поочередно складывать их на треугольники, прямоугольники и квадраты так, как изображено на рисунке. В классе замечают, что в некоторых случаях лист делится на две одинаковые геометрические фигуры таким образом, что стороны одной фигуры полностью совпадают со сторонами другой.
Следующим этапом учитель просит развернуть лист в первоначальное состояние и рассмотреть линии сгиба. Задача состоит в обнаружении связи между понятиями «ось симметрии» и «линии сгиба» в случае равенства полученных фигур. На рисунке представлены базовые сгибы техники «оригами», среди которых ось симметрии наблюдается только в первых двух.
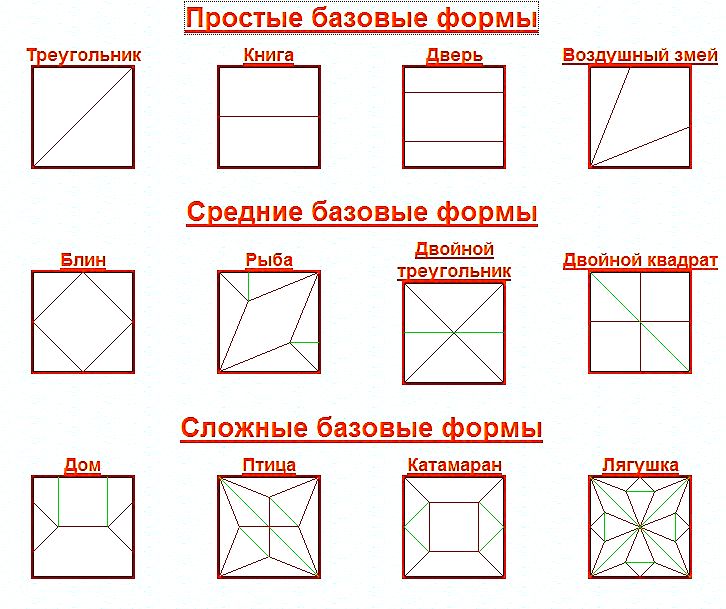
Такие упражнения позволяют сделать вывод о том, что техника «Оригами» позволяет более качественно и полноценно изучить геометрические фигуры и их свойства в начальной школе. Неоспоримый факт, что оригами и математика неразрывно связаны, так как при изготовлении различных моделей оригами мы оперируем геометрическим понятийным аппаратом.
Список литературы
1. Афонькина, Е.Ю. Все об оригами. / Е.Ю Афонькина, С.Ю. Афонькин, энциклопедия – СПб: ООО «СЗКЭО «Кристалл»», 2004г. – 272 с.
2. Выгонов, В. Геометрия и оригами / Журнал «Начальная школа» №1, 2004 г.
3. Шеремет, Г. Оригами помогает изучать математику. / Математика № 19.– 2007. с.16–18.
ЦОКО, Красноярский край (Центр оценки качества образования), [Электронный ресурс], Режим доступа: https://coko24.ru/



















