Глава 3…….
Цифровая экономика - концепция, появившаяся в самом конце XX века, связанная с распространением технологии интернет, цифровых подписей, интернет-магазинов и электронного документооборота. Прямо сейчас происходит очередная технологическая революция, которая, с одной стороны, требует новых идей и предложений по моделям и технологиям производства, а, с другой стороны, предоставляет новые возможности в области вычислений и моделирования. Так называемая цифровизация - один из путей глобализации, создания общемирового рынка товаров и услуг. Математика в этом процессе играет непосредственную роль, поскольку с одной стороны именно на математической теории сложности построены современные криптографические системы, позволяющие совершать безопасные платежи в интернете, а с другой стороны именно к математическим задачам приходят специалисты по перевозке товаров, когда хотят удешевить или убыстрить процессы перевозок. Значение математики в этом процессе невозможно переоценить, математические модели лежат в основе создания новых алгоритмов, архитектур и даже парадигм в области информационных технологий, позволяют описывать и оптимизировать производственные и технологические процессы. Синергия новых возможностей и новых вызовов создает исключительно благоприятный фон
для развития математики как классической, так и совершенно новой.
Основы математической логики
Виды доказательства в математической логике
Древние греки сформулировали основные правила логического доказательства. Они различали два вида доказательства: дедукцию и индукцию. Дедукция – это доказательство от общего к частному. Индукция – напротив, доказательство от частного к общему.
Рассмотрим классический пример. Задана так называемая большая посылка (или общее утверждение): «Все люди смертны». Также задана малая посылка (частное утверждение): «Сократ – человек». Из этих посылок методом дедукции легко получить заключение: «Сократ – смертен». В большой и малой посылках содержится достаточно информации, чтобы быть абсолютно уверенным в этом.
Если из малой посылки и заключения получают большую посылку, то такой метод доказательства называется индукцией. В малой посылке «Сократ – человек» и заключении «Сократ – смертен» не содержится достаточно информации, чтобы прийти к утверждению: «Все люди смертны». Мы можем рассматривать его только как гипотезу. Допустим, окажется, что смертен не только Сократ, но и Платон, который также является человеком. Степень нашей уверенности возрастает, однако она никогда не будет абсолютной, поскольку в будущем, возможно, родится человек, который будет жить вечно (а вдруг?).
Таким образом, дедукция обладает неоспоримым преимуществом перед индукцией. Однако научное знание, как правило, получают методом индукции, поскольку в готовом виде общие утверждения человеку никто не посылает, приходится основываться на частном опыте. Даже гениальные озарения являются результатом длительных наблюдений и размышлений.
Математики нового времени ввели еще один тип доказательства, неизвестный древнегреческим математикам, абдукцию. Это доказательство малой посылки, основанное на большой посылке и заключении. В нашем примере на основании утверждений: «Все люди смертны» и «Сократ – смертен», мы можем вывести методом абдукции утверждение, что: «Сократ – человек». Очевидно, что этот вид доказательства тоже не столь безупречен, как дедукция. Ведь Сократ вполне может оказаться котом или собакой, которые также смертны.
Логические высказывания, связки и операции
Высказывание – имеющее смысл языковое выражение, относительно которого можно утверждать, что оно либо истинно (True), либо ложно (False). Вместо слов True и False часто употребляются числа 1 и 0 соответственно.
Пример 1. Имеем два высказывания: «Дважды два четыре» и «3+5=9». Первое высказывание имеет истинное значение, а второе – ложное.
Если отвлечься от смысла высказывания, его можно обозначить буквой и рассматривать как переменную. Используя логические связки: «НЕ», «И», «ИЛИ», «ЕСЛИ ..., ТО...» и другие – можно из одних высказываний строить новые высказывания. Построение из заданных высказываний нового высказывания называется логической операцией.
Логические связки могут быть одноместные (унарные), двухместные (бинарные), трехместные (тернарные) и т. д. В алгебре логики логические операции чаще всего описываются с помощью таблиц истинности. Для одноместной операции «не» («инверсия») таблица истинности выглядит так.
Таблица 1.
«Не А» обозначается как  А, или Ā, или ~А, или !A. В табл. 2. приведены основные двухместные логические операции.
А, или Ā, или ~А, или !A. В табл. 2. приведены основные двухместные логические операции.
Таблица 2.
| Обозначение логической операции | Другие обозначения логической операции | Набор истинностных значений | Название логической операции и связки | Как читается выражение |
| А  B B | А &B А B B АB min(А,B) | 0001 | Конъюнкция, логическое умножение логическое «И» | А и B |
| А  B B | А+B max(А,B) | 0111 | Дизъюнкция, логическое сложение, логическое «ИЛИ» | А или В |
| А 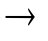 B B | А 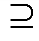 B B А 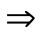 B B | 1101 | Импликация, логическое следование | Если А, то B; А имплицирует B; А влечет B |
| А  B B | А~ B А  B B А  B B | 1001 | Эквиваленция, эквивалентность, равнозначность, тождественность | А тогда и только тогда, когда B; А эквивалентно B |
| А  B B | А+B А B B | 0110 | Сумма по модулю 2, разделительная дизъюнкция, разделительное «ИЛИ» | А плюс B; либо А, либо B |
| А | B | А 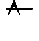 B B | 1110 | Штрих Шеффера, антиконъюнкция | Неверно, что А и B; А штрих Шеффера B |
| А B B | А  B B А  B B | 1000 | Стрелка Пирса, антидизъюнкция, функция Вебба, ф-я Даггера | Ни А, ни B; А стрелка Пирса B |
Набор истинностных значений 0001 в первой строке таблицы соответствует результатам операций:
0  0 = 0;
0 = 0;
0  1 = 0;
1 = 0;
1  0 = 0;
0 = 0;
1  1 = 1.
1 = 1.
Как известно, в арифметике вначале выполняются операции умножения или деления, а затем – сложения или вычитания. Логические связки также подчиняются подобному правилу. Приоритет применения связок возрастает в следующем порядке:  ,
, ,
, ,
,  . Чтобы изменить этот порядок, то, как и в арифметике, необходимо использовать скобки.
. Чтобы изменить этот порядок, то, как и в арифметике, необходимо использовать скобки.
Переменные и формулы в исчислении высказываний
Переменная, значениями которой являются высказывания, называется пропозициональной переменной. Понятие пропозициональной формулы вводится по индукции:
выражение, состоящее только из пропозициональной переменной, является пропозициональной формулой;
если A и B – пропозициональные формулы, то каждое из выражений  A, (A
A, (A B), (A
B), (A B), (A
B), (A B) и (A
B) и (A B) – пропозициональная формула;
B) – пропозициональная формула;
последовательность символов только тогда является пропозициональной формулой, когда она построена в соответствии с 1) и 2).
Пример 2. Примеры пропозициональных формул:
P  ((A
((A B)
B) 
 C ,
C ,
Q  ((A
((A
 C)
C)
 (A
(A  B)).
B)).
Булевы функции
Функция 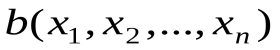 , у которой аргументы пробегают множество {0,1} и которая принимает значение из того же множества {0,1}, называется функцией алгебры логики или булевой функцией.
, у которой аргументы пробегают множество {0,1} и которая принимает значение из того же множества {0,1}, называется функцией алгебры логики или булевой функцией.
Особое значение имеют так называемые элементарные булевы функции. Двухместными элементарными булевыми функциями являются конъюнкция, дизъюнкция, импликация, сумма по модулю 2, эквиваленция, штрих Шеффера и стрелка Пирса. Символы А и B из табл. 2 следует в этом случае толковать как булевы переменные {0,1}.
Имеются две одноместные булевы функции, зависящие от x: тождественная функция 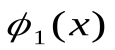 и отрицание
и отрицание 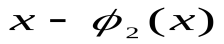 . Это элементарные функции (табл. 3).
. Это элементарные функции (табл. 3).
Таблица 3.
| x | 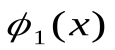 | 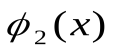 |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
Имеются две нуль-местные элементарные булевы функции: это константы 0 и 1. Каждой пропозициональной формуле можно сопоставить булеву функцию. Булева функция 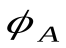 , сопоставленная пропозициональной формуле A, называется функцией истинности формулы A. Любую такую функцию можно описать с помощью соответствующей таблицы истинности (примеры – табл. 3, табл. 4, табл. 5).
, сопоставленная пропозициональной формуле A, называется функцией истинности формулы A. Любую такую функцию можно описать с помощью соответствующей таблицы истинности (примеры – табл. 3, табл. 4, табл. 5).
Пусть 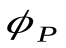 и
и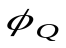 – функции истинности формул P и Q; пусть {
– функции истинности формул P и Q; пусть {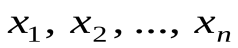 } – множество тех переменных, которые встречаются хотя бы в одной из функций
} – множество тех переменных, которые встречаются хотя бы в одной из функций 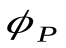 и
и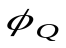 . Пропозициональные формулы P и Q называются эквивалент-
. Пропозициональные формулы P и Q называются эквивалент-
ными, если на всяком наборе (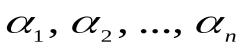 ) значений переменных
) значений переменных 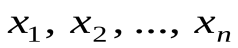 значения функций
значения функций 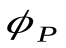 и
и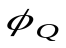 совпадают (эквивалентность обозначают как: P
совпадают (эквивалентность обозначают как: P Q).
Q).
Пример 3. Покажем эквивалентность выражений
P A
A B и Q
B и Q
 A
A B.
B.
Для этого построим таблицу истинности (табл. 4).
Таблица 4.
| A | B | 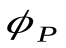 (A, B) (A, B) P A A B B | 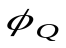 (A, B) (A, B) Q  A A B B |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
Поскольку 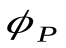 (A, B) =
(A, B) = 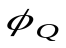 (A, B), то P
(A, B), то P  Q.
Q.
Пример 4. Покажем эквивалентность выражений
P A
A (B
(B C) и Q
C) и Q (A
(A B)
B) (A
(A C).
C).
Для этого снова построим таблицу истинности (табл. 5).
Таблица 5.
| A | B | C | 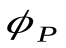 (A, B, C) (A, B, C) P A A (B (B C) C) | 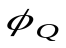 (A, B, C) (A, B, C) Q (A (A B) B) (A (A C) C) |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Поскольку 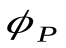 (A, B, C) =
(A, B, C) =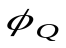 (A, B, C), то P
(A, B, C), то P  Q. Как можно видеть, в примере 3 используются двухместные функции истинности, а в примере 4 – трехместные.
Q. Как можно видеть, в примере 3 используются двухместные функции истинности, а в примере 4 – трехместные.
Основные эквивалентности:

 A
A A – правило снятия двойного отрицания;
A – правило снятия двойного отрицания;
A A
A A – идемпотентность конъюнкции;
A – идемпотентность конъюнкции;
A A
A A – идемпотентность дизъюнкции;
A – идемпотентность дизъюнкции;
A*B  B*A – коммутативность связки * (символ * является общим обозначением для связок:
B*A – коммутативность связки * (символ * является общим обозначением для связок:  ,
, ,
,  );
);
(A*B)*C  A*(B*C) – ассоциативность связки *;
A*(B*C) – ассоциативность связки *;
A (B
(B C)
C) (A
(A B)
B) (A
(A C) – дистрибутивность («distributivus» – распределительный) конъюнкции относительно дизъюнкции;
C) – дистрибутивность («distributivus» – распределительный) конъюнкции относительно дизъюнкции;
A (B
(B C)
C) (A
(A B)
B) (A
(A C) – дистрибутивность дизъюнкции относительно конъюнкции;
C) – дистрибутивность дизъюнкции относительно конъюнкции;
 (A
(A B)
B)
 A
A
 B и
B и  (A
(A B)
B)
 A
A
 B – законы де Моргана;
B – законы де Моргана;
A (A
(A B)
B) A и A
A и A (A
(A B)
B) A – законы поглощения;
A – законы поглощения;
A (
( A
A B)
B) A
A B и A
B и A (
( A
A B)
B) A
A B;
B;
A B
B
 A
A B;
B;
(A B)
B) (A
(A B)
B) (
( A
A
 B);
B);
A
 A
A False – закон противоречия;
False – закон противоречия;
A
 A
A True – закон исключенного третьего;
True – закон исключенного третьего;
A True
True A;
A;
A True
True True;
True;
A False
False False;
False;
A False
False A.
A.
Предикаты
Применяемые в математике высказывания обычно представляют собой описание свойств каких-либо математических объектов или описаний отношений, существующих между этими объектами. Для анализа закономерностей, присущих таким высказываниям, средств алгебры высказываний уже недостаточно. Поэтому вводится понятие предиката.
Индивидная (или предметная) переменная представляет собой знак, обозначающий произвольный индивид из некоторого непустого подмножества множества всех индивидов; это подмножество называется областью изменения данной переменной.
Пусть 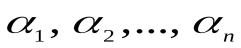 – индивиды из предметной области I. Рассмотрим какое-либо высказывание об этих индивидах и обозначим его через P(
– индивиды из предметной области I. Рассмотрим какое-либо высказывание об этих индивидах и обозначим его через P(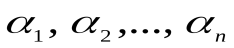 ). Если n = 1, то P(
). Если n = 1, то P(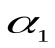 ) выражает свойство индивида
) выражает свойство индивида 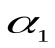 . Если n 2, то данное высказывание описывает некоторое отношение между индивидами
. Если n 2, то данное высказывание описывает некоторое отношение между индивидами 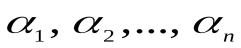 (порядок следования индивидов существенен !!!).
(порядок следования индивидов существенен !!!).
Возьмем предметные переменные 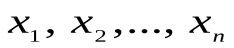 (с областями изменения
(с областями изменения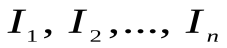 соответственно; здесь
соответственно; здесь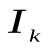 – подмножество множества I,
– подмножество множества I,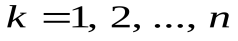 ). Выражение P(
). Выражение P(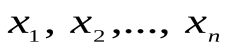 ) – и есть предикат. Здесь P может обозначать конкретный предикат (т.е. константу) или переменную-предикат, т.е. предикат в его основном смысле. Предикат, зависящий в точности от n различных предметных переменных, называется n-местным. Высказывание можно рассматривать как нуль-местный предикат, т.е. как предикат, не зависящий от предметных переменных.
) – и есть предикат. Здесь P может обозначать конкретный предикат (т.е. константу) или переменную-предикат, т.е. предикат в его основном смысле. Предикат, зависящий в точности от n различных предметных переменных, называется n-местным. Высказывание можно рассматривать как нуль-местный предикат, т.е. как предикат, не зависящий от предметных переменных.
Пример 5. «x есть четное число» – одноместный предикат; «x есть делитель y» – двуместный (бинарный) предикат.
Пусть P(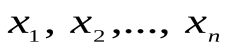 ) – предикат, а
) – предикат, а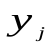 – индивидуальная константа,
– индивидуальная константа,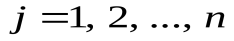 ; тогда выражение P(
; тогда выражение P(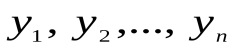 ) – называется элементарной формулой.
) – называется элементарной формулой.
Пример 6. Рассмотрим бинарные индивидуальные предикаты: 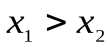 ,
,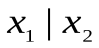 и
и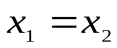 . Символы , и = означают: «больше», «есть делитель», «равно». Выражения
. Символы , и = означают: «больше», «есть делитель», «равно». Выражения 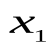 3,75 и
3,75 и 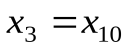 являются элементарными формулами.
являются элементарными формулами.
С элементарными формулами можно оперировать так же, как с пропозициональными переменными: к ним применимы все операции алгебры высказываний. При помощи логических связок из элементарных формул строятся новые, предикатные формулы. Сами элементарные формулы тоже считаются предикатными.
Пример 7. 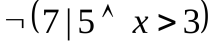 и
и 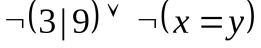 – предикатные формулы. Их можно «прочитать» следующим образом: первую – «неверно, что 7 – делитель 5 и x больше 3», вторую – «3 не делит 9 или x не равно y».
– предикатные формулы. Их можно «прочитать» следующим образом: первую – «неверно, что 7 – делитель 5 и x больше 3», вторую – «3 не делит 9 или x не равно y».
Использование только элементарных формул и операций алгебры высказываний не дает возможность преодолеть трудности, возникающие, например, при попытке сформировать на формальном логико-математическом языке следующую теорему: «уравнение x+3=8 имеет целочисленное решение». В связи с этим в рассмотрение вводятся кванторы. Используют два квантора: общности (обозначение: ; читается: «для всех...») и существования (обозначение:
; читается: «для всех...») и существования (обозначение:  ; читается: «существует...»).
; читается: «существует...»).
Таким образом, предикатные формулы строятся из элементарных формул при помощи логических связок и кванторов всеобщности и существования. Применение кванторов для построения формул осуществляется по следующей схеме. Пусть Н – предикатная формула и x– предметная переменная, которая может и не входит в формулу Н. Тогда выражения ( xH) и (
xH) и ( xH) считаются предикатными формулами (в этом случае говорят, что Н есть область действия соответствующего квантора
xH) считаются предикатными формулами (в этом случае говорят, что Н есть область действия соответствующего квантора  x или
x или  x).
x).
Приписывание спереди к предикатной формуле какого-либо квантора называется операцией навешивания квантора (или связывания квантором). Конкретное вхождение переменной x в формулу Н называется связанным, если оно либо непосредственно следует за каким-нибудь квантором, либо содержится в области действия некоторого квантора  x или
x или  x. Если вхождение переменной в формулу не является связанным, то оно называется свободным. Переменная, входящая в формулу Н, называется связанной (свободной), если в Н имеется связанное (свободное) вхождение этой переменной. Таким образом, переменная может быть одновременно и свободной и связанной (в данной формуле).
x. Если вхождение переменной в формулу не является связанным, то оно называется свободным. Переменная, входящая в формулу Н, называется связанной (свободной), если в Н имеется связанное (свободное) вхождение этой переменной. Таким образом, переменная может быть одновременно и свободной и связанной (в данной формуле).
Пример 8. Пусть Z – множество целых чисел. В предикатной формуле 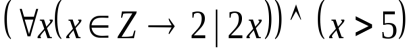 переменная x является и связанной (три ее вхождения в первый член конъюнкции – связанные), и свободной (вхождение x в формулу x 5 – свободное). Областью действия квантора
переменная x является и связанной (три ее вхождения в первый член конъюнкции – связанные), и свободной (вхождение x в формулу x 5 – свободное). Областью действия квантора x является формула
x является формула 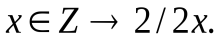
В формуле 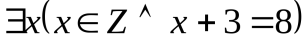 , представляющей собой истинное высказывание, все три вхождения переменной x – связанные.
, представляющей собой истинное высказывание, все три вхождения переменной x – связанные.
Семантика исчисления предикатов
Исчисление предикатов (так же как и исчисление высказываний) являются, прежде всего, языками. И эти языки можно применять не только в математике. Используя их слова, фразы и предложения, мы можем представлять свойства и отношения в окружающем мире и рассуждать о них.
Английское слово «predicate» переводится на русский язык как «сказуемое». Рассмотрим предложение: «Гамлет пронзил Лаэрта мечом». В нем слово «Гамлет» является подлежащим, «пронзил» – сказуемым, «Лаэрта» и «мечом» – дополнениями. На языке предикатов это можно выразить так:
Пронзил (гамлет, лаэрт, меч). (*)
Здесь пронзил – это предикат, а гамлет, лаэрт, меч – его термы. Такая запись похожа на обозначение функции, пронзил – аналог имени функции, а гамлет, лаэрт, меч – что-то вроде ее аргументов. Причем эти «аргументы» не равноправны между собой. «Гамлет» – это агент (тот, кто действует), он записан первым. «Лаэрт» – это объект действия, и он записан вторым. А «меч» – это инструмент, он стоит на третьем месте. В принципе, термы предиката могут быть представлены и в ином порядке (например, вначале «инструмент», потом «объект» и затем «агент»). Однако, приняв такой порядок, мы должны строго придерживаться его в дальнейшем.
Таким образом, предикат – это форма представления информации, связывающая символы (слова) с объектами реального мира (или литературного произведения). Кроме того, он содержит информацию об истинности рассматриваемого утверждения. Высказывание может быть истинным или ложным. Если герой трагедии Гамлет действительно пронзил Лаэрта мечом, то выражение (*) идентифицируется как истинное. В противном случае оно будет ложным. Предположим что мы захотели использовать этот предикат с другими константами:
Пронзил (ахилл, гектор, копье),
что равнозначно предложению: «Ахилл пронзил Гектора копьем». В общем случае мы можем записать
пронзил (X, Y, Z), (**)
где X, Y, Z – переменные. Разумеется, выражение (**) будет принимать значение «истина» не для всего возможного набора переменных, а только в том случае, если этот набор отвечает каким-то реальным (или изображаемым в литературном произведении) событиям.
Рассмотрим еще два предиката:
Любит (саша, таня),
Любит (нина, женя, люда).
Это два разных предиката, хотя они и имеют одинаковые имена. В первом случае мы имеем двухместный предикат, а во втором – трехместный. В этом и заключается причина отличия, обычно в таком случае и семантика предикатов тоже немного различная. В исчислении предикатов нет места двусмысленностям.
Приведем примеры одноместных предикатов: прекрасная (осень), вкусное (яблоко), отвратительный (скрежет). Эти предикаты описывают свойства объектов. А многоместные предикаты – соответственно отношения между объектами.
В исчислении предикатов помимо собственно самих предикатов используются еще и функции в привычном для нас смысле. Отличие между первыми и вторыми заключается в том, что предикаты возвращают значения алгебры логики: True и False (T и F), а функции – числовые значения. Например, функция плюс (два, пять) возвращает числовое значение семь, хотя по внешнему виду она ничем не отличается от предиката. Функция не может быть ни истинной, ни ложной.
Реальный мир (или воображаемый мир), литературное произведение (или математическая теория) наполнены множеством вещей, событий или местоположений. Язык сопоставляет этому многообразию определенные слова. Все, что мы описываем с помощью высказываний называется областью определения D. Истинность выражений зависит от соответствия констант, переменных, предикатов и функций объектам и отношениям в области определения.
Пусть область определения D – представляет из себя некоторое непустое множество. Интерпретация на D – это связывание логических объектов из D с каждой константой, переменной, предикатом и функциональным символом в выражении исчисления предикатов на основе следующих правил.
Каждой константе ставится в соответствие элемент из D.
Каждой переменной ставится в соответствие непустое подмножество из D; оно является областью допустимых значений для этой переменной.
Каждая функция f арности (числа операндов) m определяется для m параметров из D и задает отображение из 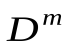 в D.
в D.
Каждый предикат p арности n определяется для n параметров из D и задает отображение из 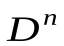 в {T, F}.
в {T, F}.
Многие грамматически правильные предложения естественных языков могут быть представлены в исчислении предикатов первого порядка с помощью символов, связок и символьных переменных. Важно заметить, что не существует уникального отображения предложений в выражения исчисления предикатов. Одно предложение может иметь любое число различных представлений. Приведем примеры некоторых преобразований.
«Если в воскресенье не будет дождя, Петя пойдет в гости к другу».
 погода (дождь, воскресенье)
погода (дождь, воскресенье) пойдет_в_гости (петя, друг)
пойдет_в_гости (петя, друг)
«Все баскетболисты – высокие».
X (баскетболист(X)высокий(X))
«Два плюс три равно пяти».
Равно (плюс(два, три), пять)
«Некоторые люди любят грибы»
X(личность (х)любит (х, грибы))
«Никто не любит платить налоги»
X любит (х, платить(налоги))
Правила логического вывода
Возможность логически выводить новые правильные выражения из набора истинных утверждений – это важное свойство исчисления предикатов. Логически выведенные выражения корректны, потому что они совместимы со всеми предыдущими интерпретациями первоначального набора выражений.
Одним из наиболее важных правил логического вывода является «MODUS PONENS» (переводится с латинского как «правило отделения»). Другие полезные правила вывода называются «MODUS TOLLENS» («правило исключения»), «Транзитивность», «Слияние», «Исключение «И»», «Введение «И»», «Универсальное инстанцирование».
Если известно, что предложения A и A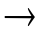 B истинны, то модус поненс позволяет вывести истинность B. Формально это записывается следующим образом:
B истинны, то модус поненс позволяет вывести истинность B. Формально это записывается следующим образом:  .
.
Согласно правилу вывода модус толленс, если известно, что A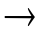 B является истинным и B ложно, то можно вывести истинность
B является истинным и B ложно, то можно вывести истинность  A. Формально:
A. Формально: 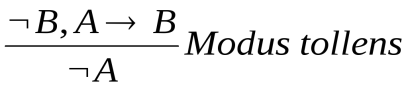 .
.
Транзитивность – если известно, что выражения A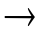 B и В
B и В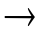 С истинны, то истинно и выражение A
С истинны, то истинно и выражение A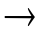 С. Формально:
С. Формально: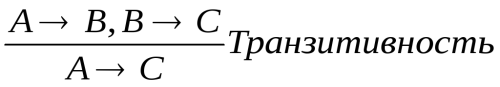 .
.
Слияние – если известно, что выражения A B и А
B и А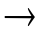 В истинны, то истинно и выражение B. Формально:
В истинны, то истинно и выражение B. Формально: 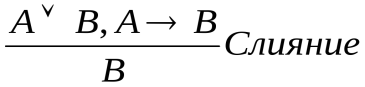 .
.
Исключение «И» – правило, позволяющее вывести истинность обоих конъюнктов на основе истинности конъюнктивного предложения. Например, если A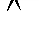 B истинно, можно сделать вывод, что A и B истинны. Формально:
B истинно, можно сделать вывод, что A и B истинны. Формально: 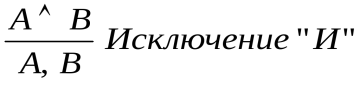 .
.
Введение «И» – позволяет вывести истинность конъюнкции из истинности ее конъюнктов. Например, если A и B истинны, то конъюнкция A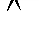 B также истинна. Формально:
B также истинна. Формально: 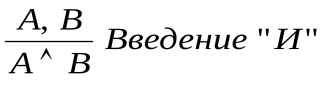 .
.
Универсальное инстанцированние сводится к следующему: если любую переменную, стоящую под квантором всеобщности в истинном предложении, заменить любым соответствующем термом из области определения, то результирующее выражение истинно. Таким образом, если «a» принадлежит той же области определения, что и Х и  Xр(Х), то можно вывести истинность р(а).
Xр(Х), то можно вывести истинность р(а).
Пример 9. Рассмотрим предложения: P  «идет дождь» и P
«идет дождь» и P Q
Q  «если идет дождь, то земля будет влажной». Согласно правилу модус поненс предложение Q
«если идет дождь, то земля будет влажной». Согласно правилу модус поненс предложение Q  «земля является влажной» является истинным, если истинны предложения P и P
«земля является влажной» является истинным, если истинны предложения P и P Q.
Q.
Пример 10. Правило модус поненс может быть также применено к выражениям, содержащим переменные. Рассмотрим в качестве примера известный силлогизм: «Все люди смертны, и Сократ – человек, поэтому Сократ – смертен».
«Все люди смертны» и «Сократ – человек» может быть представлено в исчислении предикатов следующим образом:
X(человек (X)смертный(X)),
Человек (сократ).
Поскольку Х в выражении стоит под знаком квантора всеобщности, его можно заменить любым значением из области определения Х, и при этом утверждение будет сохранять истинное значение согласно правилу универсального инстанцирования. Заменив в выражении Х на «сократ», получим следующее утверждение
Человек (сократ) смертный (сократ).
смертный (сократ).
Применив правило модус поненс, приходим к выводу: смертный (сократ).
Правило резолюции
Правило резолюции (лат. resolutio – решение): если выражения P A
A C и Q
C и Q B
B
 C являются истинными, то выражение A
C являются истинными, то выражение A В тоже истинно. Формально можем записать:
В тоже истинно. Формально можем записать:
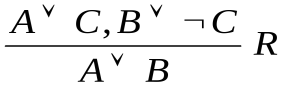 .
.
Предложения P A
A C и Q
C и Q B
B
 C называются резольвируемыми (или родительскими), предложение A
C называются резольвируемыми (или родительскими), предложение A В – резольвентой, а формулы С и
В – резольвентой, а формулы С и  С – контрарными литералами.
С – контрарными литералами.
Правило резолюции является более общим правилом логического вывода по сравнению с рассмотренными ранее. Модус поненс и многие другие правила вывода являются частными случаями правила резолюции.

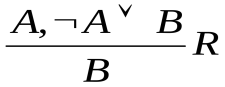
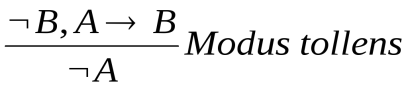
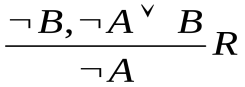
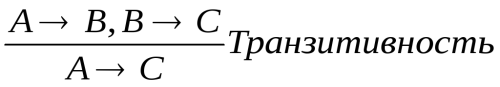
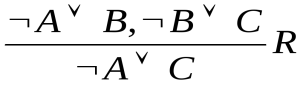
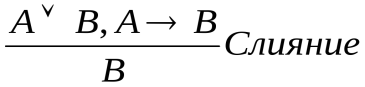
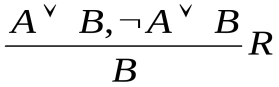
Для доказательства справедливости правила резолюции рассмотрим табл. 6.
Таблица 6.
| № | A | B | C |  P A A C C | 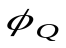 Q B B  C C | 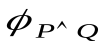
| 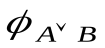
|
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 5 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 6 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Как можно видеть, значения функций 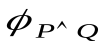 и
и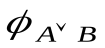 совпадают в выделенных серым цветом строках. Этого вполне достаточно для того, чтобы правило резолюции являлось справедливым.
совпадают в выделенных серым цветом строках. Этого вполне достаточно для того, чтобы правило резолюции являлось справедливым.
Принцип резолюции описывает способ обнаружения противоречий в базе данных дизъюнктивных выражений. В его основе лежит идея «доказательства от противного». Процесс доказательства состоит из следующих этапов.
Исходные аксиомы приводятся к дизъюнктивной форме.
К набору аксиом добавляется отрицание доказываемого утверждения в дизъюнктивной форме.
Выполняется совместное разрешение этих дизъюнктов, в результате чего получаются новые основанные на них дизъюнктивные выражения.
Генерируется пустое выражение, означающее противоречие.
Подстановки, использованные для получения пустого выражения, свидетельствуют о том, что отрицание отрицания – истинно.
Пример 11. Докажем, что утверждение «Мухтар смертен» следует из утверждений «Мухтар – собака», «Собаки – это животные» и «Все животные смертны». Преобразовывая эти аксиомы в предикатную форму и применяя правило модус поненс, получим следующее.
Собаки – это животные:  Х(собака(Х)
Х(собака(Х) животное(Х)).
животное(Х)).
Мухтар – собака: собака (мухтар).
Наоснове модус поненс и подстановки (мухтар/Х) получим: животное (мухтар).
Все животные смертны:  Y(животное(Y)
Y(животное(Y) умрет(Y)).
умрет(Y)).
На основе модус поненс и подстановки (мухтар/Y) получим: умрет (мухтар).
По принципу резолюции эти предикаты необходимо преобразовать в дизъюнктивную форму.
| Предикатная форма | Дизъюнктивная форма |
|  Х(собака(Х) Х(собака(Х) животное(Х)) животное(Х)) | 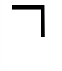 собака(Х) собака(Х) животное(Х) животное(Х) |
| Собака (мухтар) | собака (мухтар) |
|  Y(животное(Y) Y(животное(Y) умрет(Y)) умрет(Y)) | 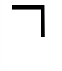 животное(Y) животное(Y) умрет(Y) умрет(Y) |
Полученную базу данных можно записать в виде конъюнктивной нормальной формы (КНФ) – т.е. в виде конъюнкции дизъюнктов.
(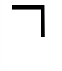 собака(Х)
собака(Х) животное(Х))
животное(Х)) (
(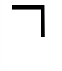 животное(Y)
животное(Y) умрет(Y))
умрет(Y)) (собака(мухтар)).
(собака(мухтар)).
Контрольные вопросы для самоподготовки
Логические переменные, логические функции.
Таблица истинности. Назначение таблиц истинности. Правило построение таблицы истинности.
Конъюнкция. Определение, обозначение, описание на естественном языке, таблица истинности.
Дизъюнкция. Определение, обозначение, описание на естественном языке, таблица истинности.
Инверсия. Определение, обозначение, описание на естественном языке, таблица истинности.
Импликация. Определение, обозначение, описание на естественном языке, таблица истинности.
Эквиваленция. Определение, обозначение, описание на естественном языке, таблица истинности.
Виды формул алгебры высказываний (нейтральные, тождественно истинные, тождественно ложные). Равносильные формулы.
Тождественные преобразования. Законы логики высказываний (13 законов).
Решение логических задач (составления таблиц истинности, тождественные преобразования).
Задания для самостоятельной работы студентов
Представить логическими формулами следующие высказывания:
а) «Сегодня суббота или воскресенье».
Решение.
Пусть A — «сегодня суббота», а B — «сегодня воскресенье». Тогда «сегодня суббота или воскресенье» представимо формулой: A ⊕ B . (Это сложное высказывание состоит из двух простых высказываний A и B, соединенных связкой «или» в разделительном смысле.)
б) «Идет снег или дождь».
в) «Если идет дождь, то крыши мокрые».
г) «Что в лоб, что по лбу».
д) «В квартире грязно и холодно».
е) «Если допоздна работаешь с компьютером и при этом пьешь много кофе, то утром просыпаешься в дурном настроении или с головной болью».
2. Пусть даны высказывания: A — «число 9 делится на 3», B — «число 10 делится на 3». Требуется определить значения истинности следующих высказываний:
1) B A → ; 2) ¬ A B → ; 3) ¬ B → ¬ A.
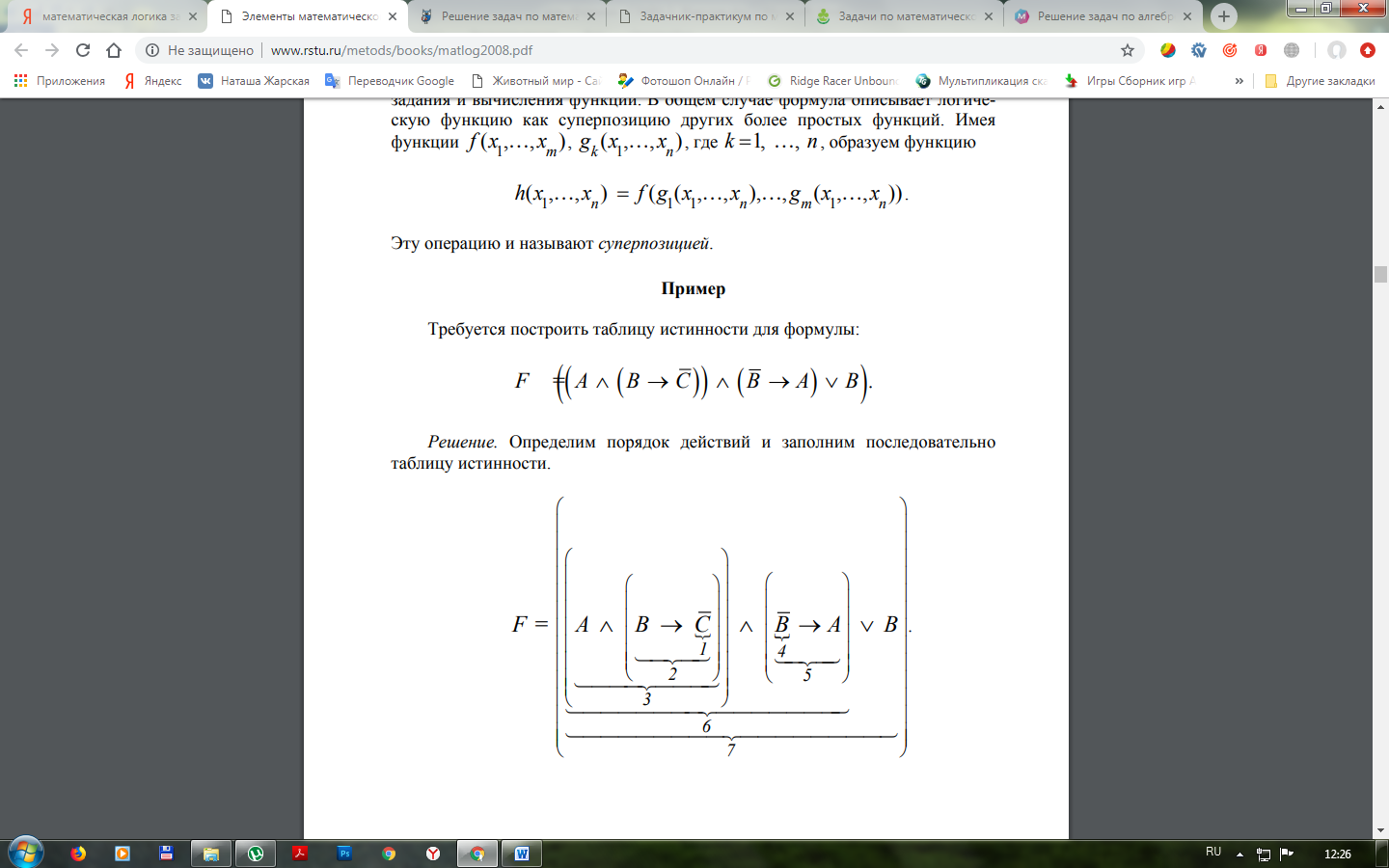
3. Построить таблицу истинности для формулы:
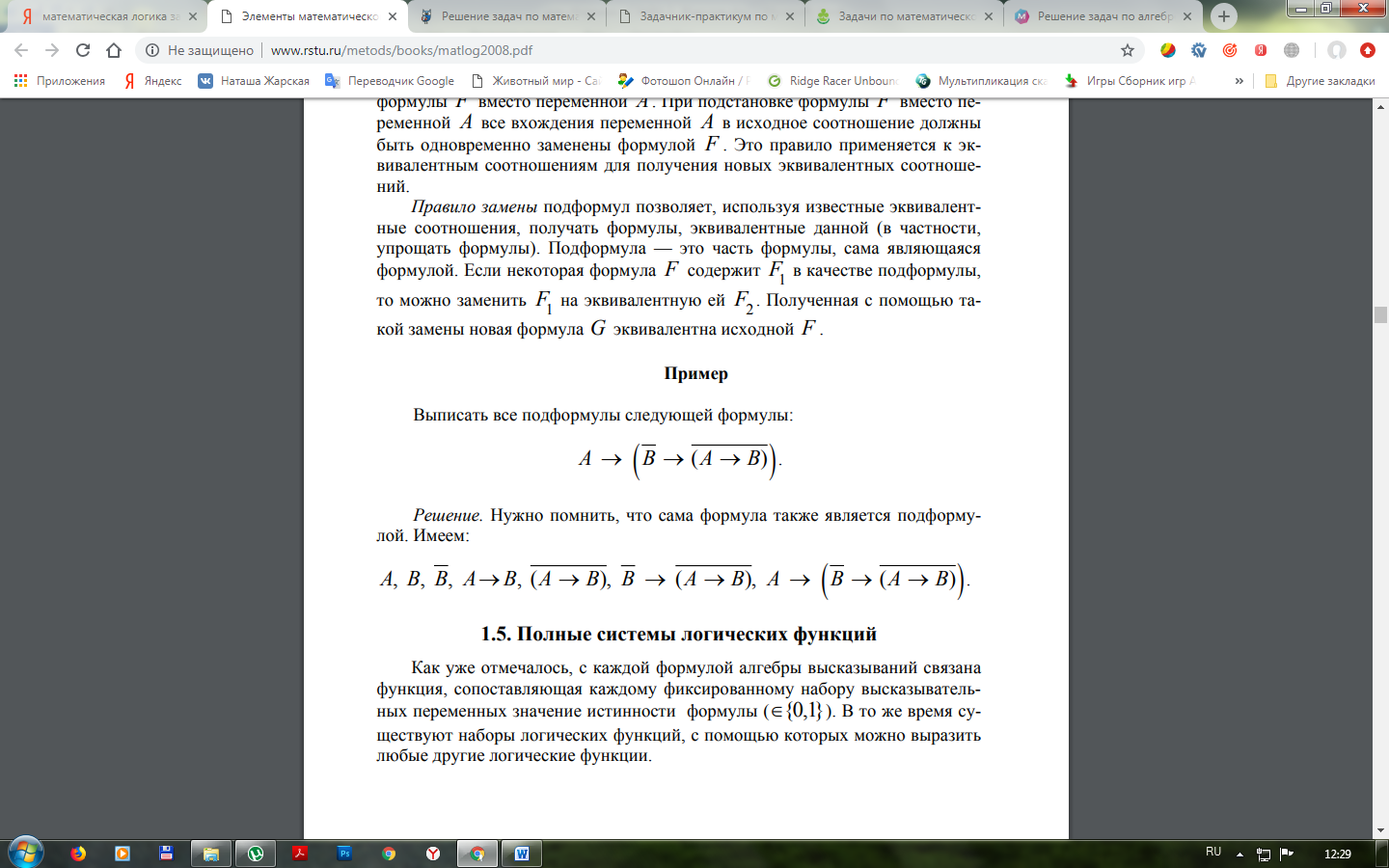
4. Выписать все подформулы следующей формулы:
5. Выяснить, является ли следующая формула тождественно истинной:

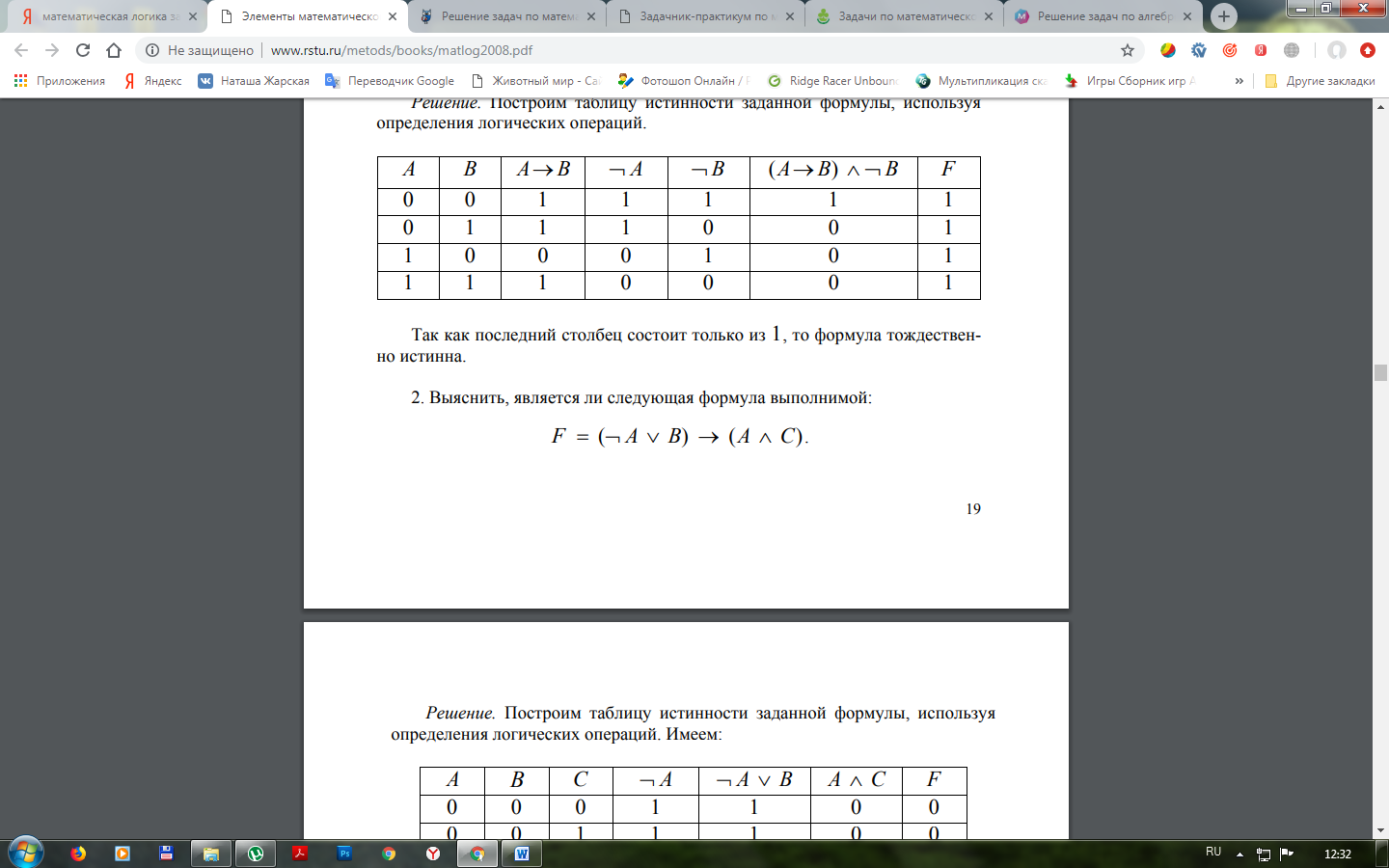
6. Выяснить, является ли следующая формула выполнимой:
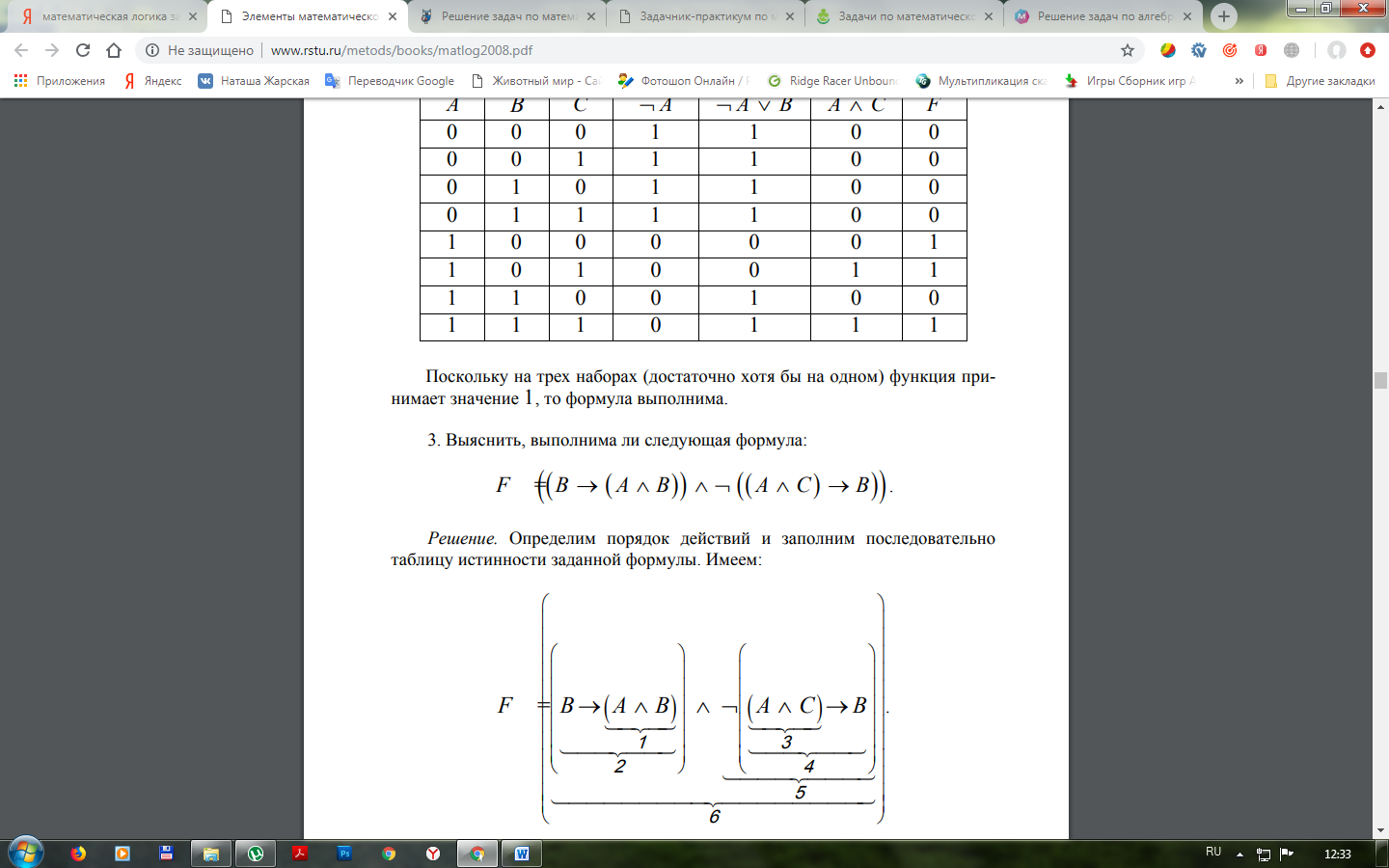
7. Выяснить, выполнима ли следующая формула:
8. Определить, кто из четырех студентов сдал экзамен, если известно, что:
1) если первый сдал, то и второй сдал;
2) если второй сдал, то третий сдал или первый не сдал;
3) если четвертый не сдал, то первый сдал, а третий не сдал;
4) если четвертый сдал, то и первый сдал.
9. Доказать общезначимость следующей формулы логики предикатов:
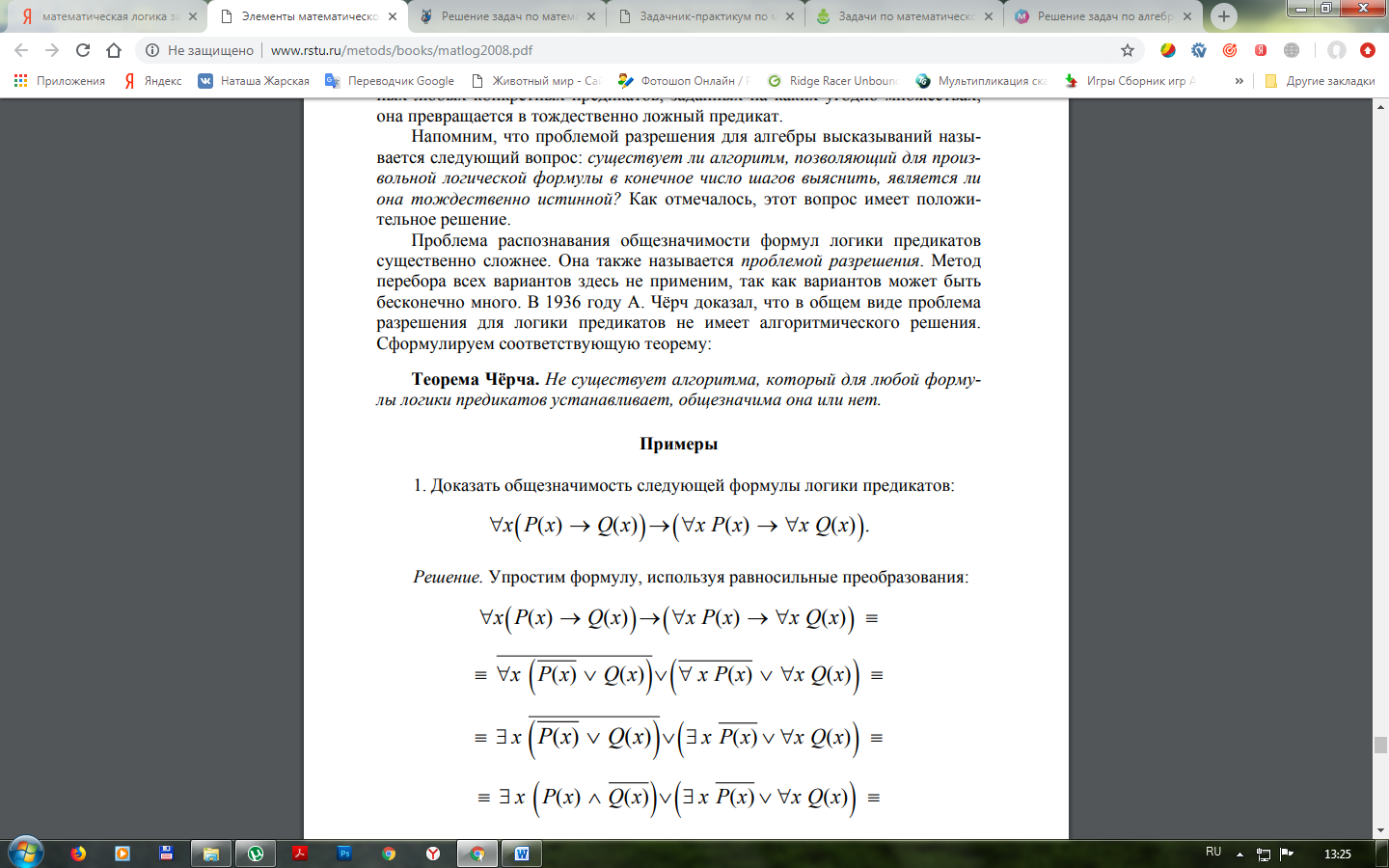
10. Доказать тождественную ложность следующей формулы:
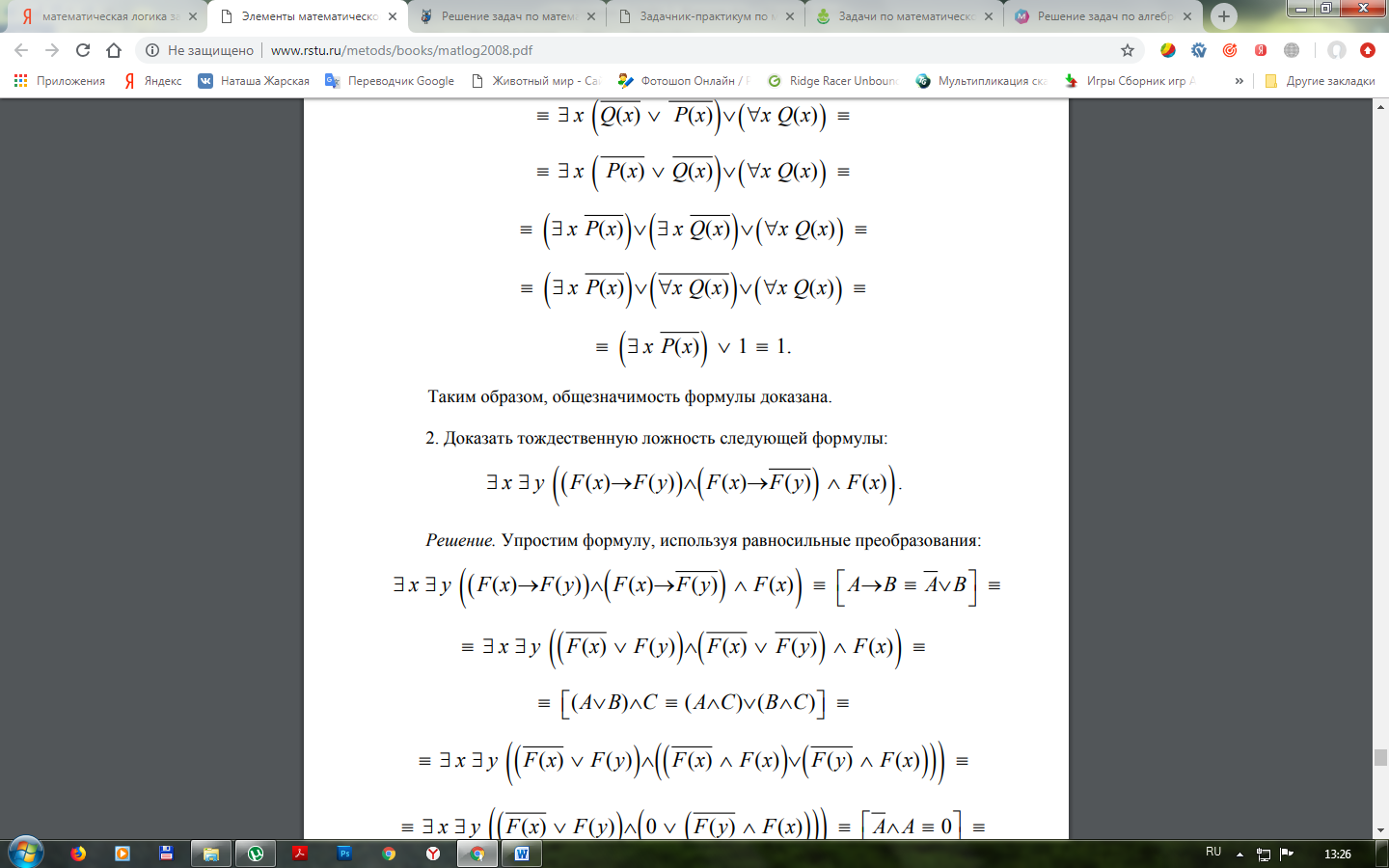
11. Построить таблицы истинности для следующих схем:
1) (X Y) (X Y X);
2) X (Y X) X;
3) ((X Y) Y) (X Y);
4) X (Y Z)) ((X Y) (X Z));
5) X (Y X) ((Y X) Y).
12. Преобразовать к возможно более простой форме:
1) (X Y) (X Y X);
2) (X Y) (X Y) X;
3) (X Y) (Y X) (X Y);
4) (X Y) (Y X) (Z X);
5) X Z X Z Y Z X Y Z.
13. Найти какое-нибудь предложение с одной свободной числовой переменной, которое выполняется для всех значений переменной, кроме 3, 5, 17.
14. Изобразить геометрическое место точек координатной плоскости Oxy, для которых:
1) x 0; 5) x 0 y 0;
2) y 0; 6) y 0 x 0;
3) x 0 y 0; 7) x 0 y 0.
4) x 0 y 0;
15. Докажите, что:
1. (x)(x 2 + 1 2x).
2. (x)(x 1 x 2 x).
3. (x)(0 x 2
4. (x)(x 4 – x 3 + x 2 – x + 1 0).
5. (x)(y)(x 2 + 2xy + 3y 2 + 2x + 6y + 4 0).
6. (x)(y)(x – y 4 x 2 – 5x y – 5).
7. (x)(2x + 3 = 7).
8. (x)(–2x 1).
9. (x)(x 2 – 2x 0).
10. (x)(x + x 1 = 5,2).
Рекомендуемая литература для самоподготовки
Гисин В.Б. Дискретная математика [электронный ресурс]: учебник и практикум для академического бакалавриата / В.Б. Гисин. – М.: Юрайт, 2017. – 383 с.
Библиотечно – информационный комплекс Финуниверситета при Правительстве РФ. http://library.fa.ru.
Электронная библиотека Финансового университета (ЭБ) http://elib.fa.ru/
(http://library.fa.ru/files/elibfa.pdf)
http://math.kpfu.ru
https://studfiles.net























