© 2020 1322 35


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 10.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Стенд " В мире математики"
Материал можно использовать для оформления стенда к " Недели математики"
Просмотр содержимого документа
«Aforizmi»
Математики о математике и не только...

-
В математике следует помнить не формулы, а процессы мышления.
В. П. Ермаков
-
Нельзя быть математиком, не будучи в то же время и поэтом в душе.
С. Ковалевская
-
Разумеется, хорошая математика всегда красива.
П. Д. Коэн
-
Математику нельзя изучать, наблюдая, как это делает сосед! А. Нивен
-
Мыслить последовательно, судить доказательно, опровергать неправильные выводы должен уметь всякий: физик и поэт, тракторист и химик. Э. Кольман
-
Математика принадлежит к числу тех наук, которые ясны сами по себе. К. Якоби
-
При решении задачи плохой план часто оказывается полезным: он может вести к лучшему плану. Д. Пойа
-
В конце концов, окружность бесконечно большого круга и прямая линия - одно и то же. Г. Галилей
-
Математика похожа на мельницу: если вы засыпете в нее зерна пшеницы, то получите муку, если же засыпете отруби, отруби и получите.(Андру Филлинг Хаксли)
-
Нельзя быть настоящим математиком, не будучи немного поэтом.(Карл Вейерштрасс)
-
Математика является учением об отношениях между формулами, лишенными какого бы то ни было содержания. (Давид Гильберт)
-
С тех пор, как математики взялись за Теорию относительности, я сам перестал ее понимать. (А. Эйнштейн)
-
Если теорему так и не смогли доказать, она становится аксиомой. (Евклид)
-
Математические науки, естественные науки и гуманитарные науки могут быть названы, соответственно, науками сверхъестественными, естественными и неестественными. (Лев Давидович Ландау)
-
Всякий знает, что такое кривая, пока не выучится математике настолько, что вконец запутается в бесконечных исключениях. (Феликс Клейн)
-
Мнимые числа - это прекрасное и чудесное убежище божественного духа, почти что сочетание бытия с небытием. (Готфрид Вильгельм Лейбниц)
-
Доказательство называется строгим, если таковым его считает большинство математиков. (Моррис Клайн)
-
Легче найти квадратуру круга, чем перехитрить математика. (Огастес де Морган)
-
Математическая истина, независимо от того, в Париже или в Тулузе, одна и та же. (Блез Паскаль)
-
В математике нет символов для неясных мыслей. (Анри Пуанкаре)
-
Чистая математика - это такой предмет, где мы не знаем, о чем мы говорим, и не знаем, истинно ли то, что мы говорим. (Бертран Рассел)
-
Законы математики, имеющие какое-либо отношение к реальному миру, ненадежны, а надежные математические законы не имеют отношения к реальному миру. (Альберт Эйнштейн)
-
Математик кое-что может, но, разумеется, не то, что от него хотят получить в данный момент. (Альберт Эйнштейн)
-
Математика - это единственный совершенный метод водить самого себя за нос. (Альберт Эйнштейн)
-
С тех пор как за теорию относительности принялись математики, я ее уже сам больше не понимаю. (Альберт Эйнштейн)
-
Существует поразительная возможность овладеть предметом математически, не поняв существа дела.(Альберт Эйнштейн)
-
Я с дрожью ужаса отворачиваюсь от ваших несчастных проклятых функций, у которых нет производных. (Шарль Эрмит)
-
Удачная математическая шутка лучше, чем дюжина заурядных работ; она является одновременно и лучшей математикой. (Джон Литлвуд )
-
Образование - это то, что остается, когда забываешь все, что изучал в школе. Альберт Эйнштейн
-
Фундаментальное исследование - это то, что делаешь, когда не знаешь, что собираешься сделать. Ч. Уилсон
-
Чем меньше бог вмешивается в дела мира и науки, тем лучше для науки и для авторитета бога. Л. Эйлер
-
Если кто-либо хочет кратким и выразительным словом определить само существо математики, тот должен сказать, что это наука о бесконечности. Анри Пуанкаре
-
Математика является учением об отношениях между формулами, лишенными какого бы то ни было содержания. Давид Гильберт
-
Математика - это наука о хитроумных операциях, производимых по специально разработанным правилам над специально придуманными понятиями. Ясно, что особенно важная роль при этом отводится придумыванию новых понятий. Запас интересных теорем в математике быстро исчерпался бы, если бы их приходилось формулировать лишь при помощи понятий, содержащихся в аксиомах. Ю. П. Вигнер
-
Чистая математика - это такой предмет, где мы знаем, о чем мы говорим, и не знаем, истинно ли то, о чем мы говорим. Бертран Рассел
-
Я не мог понять содержания вашей статьи, так как она не была оживлена иксами и игреками. У. Томсон (лорд Кельвин)
-
Математика представляет собой собрание выводов, которые могут быть применены к чему угодно. Бертран Рассел
-
Известный польский математик Гуго Штейнгаус шутливо утверждает, что существует закон, который формулируется так: математик сделает это лучше. А именно, если поручить двум людям, один из которых математик, выполнение любой незнакомой им работы, то результат всегда будет следующим: математик сделает ее лучше.
-
Из дома реальности легко забрести в лес математики, но лишь немногие способны вернуться обратно.(Хуго Штейнгаус)
-
Легкость математики основана на возможности чисто логического ее построения, трудность, отпугивающая многих, - на невозможности иного изложения.(Хуго Штейнгаус)
-
Между духом и материей посредничает математика. (Хуго Штейнгаус)
-
Легкость математики основана на возможности чисто логического ее построения, трудность, отпугивающая многих, - на невозможности иного изложения. Хуго Штейнгаус
-
В глазах непосвященного математические символы словно вражеские штандарты, развивающиеся над, казалось бы, неприступной цитаделью. М. Клайн
-
Геометрия - это искусство хорошо рассуждать на плохо выполненных чертежах. Нильс Г. Абель
-
Искусство решать геометрические задачи чем-то напоминает трюки иллюзионистов - иногда, даже зная решение задачи, трудно понять, как можно было до него додуматься. И. Д. Новиков
Не математики о математике
-
В голове Архимеда было больше воображения, чем в голове Гомера. (Вольтер).
-
Процветание и совершенство математики тесно связаны с благосостоянием государства. (Наполеон).
-
Какая наука может быть более благородна, более восхитительна, более полезна для человечества, чем математика? (Франклин).
-
Математики похожи на французов: чтобы вы ни сказали, они все переведут на свой собственный язык. Получится нечто противоположное. (Гете).
-
Стоит только показать, что какая-либо вещь невозможна, как найдется математик, который ее сделает. (У. У. Сойер)
-
Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой. (Леонардо да Винчи)
-
Если мы действительно что-то знаем, то мы знаем это благодаря изучению математики. (Пьер Гассенди)
-
Математики похожи на французов: что бы вы ни сказали, они все переведут на собственный язык. Получится нечто противоположное. (Иоганн Вольфганг Гете)
-
В каждой естественной науке заключено столько истины, сколько в ней математики. (Иммануил Кант)
-
Подобно тому как все искусства тяготеют к музыке, все науки стремятся к математике. (Джордж Сантаяна)
-
Математика может открыть определенную последовательность даже в хаосе. (Гертруда Стайн)
-
Математики похожи на влюбленных - достаточно согласиться с простейшим утверждением математика, как он выведет следствие, с которым вновь прийдется согласиться, а из этого следствия - еще одно. (Бернар Ле Бовье де Фонтенель)
-
Разве вы не математик? Нет. Тогда мне не о чем с вами говорить. Я разговариваю лишь с теми, кто владеет методом математического анализа. (Анатоль Франс)
-
Когда разговариваешь с математиком, можно не иметь представления о математике. Но при этом совершенно необходимо чувство юмора и сознание своего ничтожества... К. Дзевановский
-
Математика - это наука о хитроумных операциях, производимых по специально разработанным правилам над специально придуманными понятиями. Ясно, что особенно важная роль при этом отводится придумыванию новых понятий. Запас интересных теорем в математике быстро исчерпался бы, если бы их приходилось формулировать лишь при помощи понятий, содержащихся в аксиомах. (Юджин Пол Вигнер)
Математика в афоризмах
Как же я раньше не догадывался, что это так просто? То есть не счастье, а приближение к нему, то, что в математике называется асимптотой: линия, никогда не совпадающая с кривой, но тесно приближающаяся к ней. Асимптота счастья – вот чего надо искать в жизни.
М. Алданов
Холодные числа, внешне сухие формулы математики полны внутренней красоты и жара сконцентрированной в них мысли.
А.Д.Александров

Музыка – наука, которая говорит о цифрах, находящихся в звуках
Алкуин Флакк Альбин(ок.735-804)
Математика. Как жаль, что я её не знаю. От формул меня сразу начинает поташнивать.
Н. Амосов, врач
И сильно возлюбив искусство числительное, помыслил я, что без числа никакое рассуждение философское не слагается, всей мудрости матерью его почитая.
Анания из Ширака (армянский математик VII века)
Алгебра даёт общую “отмычку”, которой открываются любые задачные “замки”, тогда как арифметика подбирает к каждой задаче свой “ключ”.
И.К.Андронов
Имеются три умозрительных учения: математика, учение о природе, учение о божественном.
Аристотель.
Пифагорейцы, занявшись математикой, первые развили её и, овладев ею, стали считать её начала началами всего существующего.
Аристотель.
Без математики люди жили бы в первобытном состоянии.
М. Артёмов, ученик 5 класса КМКК
Нельзя требовать от банкира Нусингена остроумного разговора, как не должно ожидать поэтических суждений от математика.
О.Бальзак
Предохранить гимназистов от угрожающего им отупения могли бы математика и физика, но они были пасынками в гимназической программе.
О.Бальзак
…вист и бостон - головоломка, путаница, хуже всякой алгебры.
О.Бальзак
…продолжал он с той упрямой логичностью, которая свойственна математикам.
О.Бальзак
Разве математики…не имеют своих тайн и, более того, своих неприятностей и противоречий?
Беркли
Я не собираюсь вызывать инквизицию против математиков, я хочу лишь доказать, как мало именно они имеют права требовать строгого доказательства того, во что люди верят.
Беркли
Нелепость школьной математики происходит …от того, что она изучается в школе как предмет, между тем как она должна изучаться исключительно как метод познания и технический язык.
П.П.Блонский
Незначительно ещё число философов в наши дни, чьё математическое знание простиралось бы дальше положения, что А равно А. Ещё меньше число математиков, готовых признать, что их собственная наука может быть поднята на более высокую ступень совершенства при помощи философии, и которые согласились бы, что их наука выиграла бы, если бы удалось многие встречающиеся в ней понятия, оставляемые без всякого объяснения, как общеизвестные, разложить на их составные части и множество положений, рассматриваемых либо без доказательства, либо как очевидные, вывести из их объективных оснований, т.е. из некоторых чистых понятийных истин, которые намного более общи, чем они.
Бернард Больцано (1781-1848), математик, философ, теолог
Формула подчас кажется более мудрой, чем выдумавший её человек.
Бернард Больцано
Математика – это больше, чем наука, это язык.
Н.Бор
Можно выразить надежду, что открылась новая эра взаимного стимулирования математики и механики. Наверное, физики сначала будут сожалеть, что в познании атома нам не миновать ограничения обычных способов описания природы. Но хочется думать, что это сожаление сменится чувством благодарности к математике, дающей нам и в этой области инструмент для продвижения вперёд.
Н.Бор
.Смысл - там, где змеи интеграла
Меж цифр и букв, меж d и f!
В.Брюсов
Высь, ширь, глубь. Лишь три координаты.
Мимо них где путь? Засов закрыт.
С Пифагором слушай сфер сонаты,
Атомам дли счёт, как Демокрит.
В.Брюсов
Примем за аксиому: без жилища человек существовать не может.
М. Булгаков
Со времён греков говорить “математика” - значит говорить “доказательство”.
Н. Бурбаки
В своей аксиоматической форме математика представляется скоплением абстрактных форм – математических структур и оказывается (хотя и неизвестно почему),что некоторые аспекты экспериментальной действительности как будто в результате предопределения укладываются в некоторые из этих форм.
Н. Бурбаки
Вот уже 25 веков математики имеют обыкновение исправлять свои ошибки и видеть в этом обогащение, а не обеднение своей науки; это даёт им право смотреть в грядущее спокойно.
Н. Бурбаки
То, что между экспериментальными явлениями и математическими структурами существует тесная связь – это, как кажется, было совершенно неожиданным образом подтверждено недавними открытиями современной физики, но нам совершенно неизвестны причины этого (если только этим словам можно приписать какой-либо смысл) и, быть может, мы их никогда не узнаем.
Н. Бурбаки
Введя эти неизбежные поправки, можно лучше понять внутреннюю жизнь математики, понять то, что создаёт её единство и вносит в неё разнообразие, понять это большой город, чьи предместья не перестают разрастаться несколько хаотическим образом на окружающем его пространстве, в то время как центр периодически перестраивается, следуя каждый раз всё более и более ясному плану и стремясь ко всё более и более величественному расположению, в то время как старые кварталы с их лабиринтом переулков сносятся для того, чтобы проложить к окраине улицы всё более прямые, всё более широкие, всё более удобные.
Н. Бурбаки
Искусство – это завуалированная алгебра, отнимающая жизнь у тех, кто стремится приподнять её покрывало.
Бурдель, (1861-1929), скульптор
Я глубоко почитаю математику, потому что знакомые с нею видят в ней средство к пониманию всего существующего.
Бхаскара
Человек, не знающий математики, не способен ни к каким другим наукам. Более того, он даже неспособен оценить уровень своего невежества.
Роджер Бэкон(1214-1294)
Редко вообще можно найти учителей математики, да и те следуют очень плохой методе и преподают много ненужного.
Роджер Бэкон
…одна может очистить разум и сделать учащегося способным к восприятию знания.
Роджер Бэкон о математике
…будучи самой лёгкой, она представляет введение к более трудным наукам.
Роджер Бэкон о математике
…в ней вещи, известные нам, тождественны с вещами, известными природе.
Роджер Бэкон о математике
…дверь и ключ к науке.
Роджер Бэкон о математике
Она предшествует другим наукам о природе, ибо изучает количество, которое воспринимается интуитивно.
Роджер Бэкон о математике
…математика есть азбука натуральной философии.
Роджер Бэкон
Только розгами можно вогнать ученикам четыре первых теоремы эвклидовых “Элементов”, а пятая уже называется elefuga – бегство несчастного!
Роджер Бэкон
Аристотель прекрасно сказал, что “физика и математика рождают практику, т.е. механику”.
Ф.Бэкон
Поскольку же человеческий ум от природы (к великому, правда, ущербу для развития науки) предпочитает свободное поле общих истин густым зарослям и лесам частных проблем, то трудно было найти что-либо увлекательнее и приятнее математики для того, чтобы удовлетворить это стремление человеческого ума выйти на широкий простор размышлений.
Ф.Бэкон
Представляется более правильным, имея в виду огромное значение математики и для физики, и для метафизики, и для механики, и для магии отнести её в приложения ко всем этим наукам и определить как вспомогательную для них дисциплину. Сделать это нас в какой-то мере побуждает и общеизвестное высокомерие и самодовольство математиков, стремящихся к тому, чтобы их наука фактически господствовала над физикой. Ведь как-то так случилось, что математика и логика, которые должны были бы быть служанками физики, теперь, кичась перед нею своею точностью, претендуют на господство в ней.
Ф.Бэкон
В природе существует много такого, что не может быть ни достаточно глубоко понято, ни достаточно убедительно доказано, ни достаточно умело и надёжно использовано на практике без помощи и вмешательства математики.
Ф.Бэкон
По мере того как физика день ото дня будет приумножать свои достижения и выводить новые аксиомы, она будет во многих вопросах нуждаться всё в большей помощи математики; и это приведёт к созданию ещё большего числа областей смешанной математики.
Ф.Бэкон
Удивительное дело, и тем не менее это неоспоримый факт, что существует очень много людей, у которых логическая часть ума (если можно так выразиться) действует хорошо, математически же – очень плохо, т.е. люди способны достаточно умно судить о тех последствиях, которые могут вытекать из того или иного поступка или действия, но они совершенно не знают цену вещам… С точки зрения истинного математического образования души прежде всего важно точно знать, что должно стоять на первом месте для достижения и приумножения счастья каждого, что на втором и т.д.
Ф.Бэкон
Физика и математика всегда помогали одна другой, и развитие их часто не разделимо.
С.И.Вавилов
Бог существует, поскольку математика, несомненно, непротиворечива, но существует и дьявол, поскольку доказать её непротиворечивость мы не можем.
Г.Вейль
Чистая математика обладает нечеловеческим свойством звёздного света – сверкающего, яркого, но холодного.
Г.Вейль
Математика играет весьма существенную роль в формировании нашего духовного Математическая символика – самый надёжный язык; избежать её можно только ценой длинных перифраз, которые всё равно не будут понятны профану и которые поймёт лишь подготовленный читатель, переведя их обратно в символы.
. Н.Винер
Мы, математики, нуждаемся лишь в таких недорогих материалах, как бумага и, быть может, типографская краска.
. Н.Винер
Ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства.
Леонардо да Винчи
Нет достоверности там, где нельзя применить одну из математических наук.
Леонардо да Винчи
облика. Занятие математикой – подобно мифотворчеству, литературе или музыке – это одна из наиболее присущих человеку областей его творческой деятельности, в которой проявляется его человеческая сущность, стремление к интеллектуальной сфере жизни, являющейся одним из проявлений мировой гармонии.
Г.Вейль
Он отнёсся к крушению, как математик к задаче, которую необходимо решить и определить неизвестное.
Ж.Верн
Математический язык удивительно хорошо приспособлен для формулировки физических законов. Это чудесный дар, который мы не понимаем и которого не заслуживаем. Нам остаётся лишь благодарить за него судьбу и надеяться, что и в своих будущих исследованиях мы сможем по-прежнему пользоваться им. Мы думаем, что сфера его применимости ( хорошо это или плохо) будет непрерывно возрастать, принося нам не только радость, но и новые головоломные проблемы…
Юджин Пол Вигнер (физик, лауреат Нобелевской премии)
…Великий математик полностью владеет всем арсеналом допустимых приёмов мышления и, действуя подчас весьма рискованно, балансирует на самой грани допустимого.Уже одно то,что его безрассудство не завело его в пучину противоречий, само по себе чудо. Трудно поверить, что дарвиновский процесс естественного отбора довёл наше мышление до такой степени, совершенства, которой оно, судя повсему, обладает.
Юджин Пол Вигнер
Невероятная эффективность математики в естественных науках есть нечто граничащее с мистикой.
Юджин Пол Вигнер (физик)
Либерализм и ультрароялизм слышатся в нотах музыканта и угадываются в А+В бесстрастного математика.
П.Вяземский
Книга природы раскрыта перед нами, но она написана не теми буквами, из которых состоит наш алфавит; её буквы – это треугольники, четырёхугольники, круги, шары.
Г.Галилей
Если бы мне пришлось начать вновь своё обучение, то я последовал бы совету Платона и принялся бы сперва за математику как науку, требующую точности и принимающую за верное только то, что вытекает как следствие из доказанного.
Г.Галилей
Подобно другим естественным наукам, математика представляет собой игру, в которую мы играем с окружающим миром, с Вселенной. Самые лучшие математики и самые хорошие преподаватели - это, очевидно, люди, которые прекрасно разбираются в ее правилах, а также получают удовольствие от самого процесса игры.
М. Гарднер
Никогда не было недостатка в хулителях математики.
М. Гарднер
Математика своей определённостью и ясностью как бы снова вводила его в знакомое, хорошо исследованное русло.
Гарин-Михайловский
Если мы действительно что-то знаем, то мы знаем это благодаря изучению математики. Кто пропитался с детства математикой в такой мере, что усвоил себе её неопровержимые доказательства, тот так подготовлен к восприятию истины, что нелегко допустит какую-нибудь фальшь.
П. Гассенди (1592-1655)
Вкус к абстрактным наукам вообще и сверх всего к тайнам чисел встречается крайне редко: одиночка не удивляется этому; чарующее обаяние этой возвышенной науки открывается только тем, кто имеет смелость войти в неё глубоко.
Гаусс
В математике нет истинных противоречий.
Гаусс
Математика – царица наук; теория чисел – царица математики.
Гаусс
Математика – наука точная потому, что она наука тощая.
Гегель
Развитие математического аппарата квантовой механики предшествовало физическому пониманию атомной физики.
В. Гейзенберг
Первичным языком, который вырабатывают в процессе научного усвоения фактов, является в теоретической физике обычно язык математики, а именно математическая схема, позволяющая физикам предсказывать результаты будущих экспериментов.
В. Гейзенберг
Математика, подобно жернову, перемалывает то, что под него засыпают, и как, засыпав лебеду, вы не получите пшеничной муки, так, исписав целые страницы формулами, вы не получите истины из ложных предпосылок.
Гексли
Интерес способен заставить отрицать самые очевидные теоремы геометрии.
Гельвеций
Можно вычислить вероятности достоверностей истории так же, как вероятности игры.
Гельвеций
В наших чувствах находятся матрицы наших идей
Гельвеций
Геометрия – это интуиция.
Гельмгольц
Ведь генерал-бас есть не что иное, как своего рода прикладная математика. В гармонии и ритме отношения целых чисел, иногда даже логарифмы играют выдающуюся роль.
Г. фон Гельмгольц
Музыка и математика суть самые резкие контрасты, какие только можно найти в духовной жизни человека. И всё же одна из них опирается на другую, и они связаны друг с другом, как бы доказывая последовательность всех проявлений нашей души.
Г.фон Гельмгольц
Трудно отделаться от ощущения, что эти математические формулы существуют независимо от нас и обладают своим собственным разумом, что они умнее нас, умнее тех, кто открыл их. И что мы извлекаем из них больше, чем было в них первоначально заложено.
Г.Герц (1857-1894), физик
…мы рассматриваем математику как важный компонент культуры.
И.Гельфанд
Математика - это марафон.
А.Гельфонд, математик
Математика в изречениях
Математику можно определить как предмет, в котором всегда трудно понять, о чём идёт речь и является ли истиной то, что мы утверждаем. (Б.Рассел)
Математика – всего лишь игра в которую играют согласно простым правилам и пользуются при этом ничего не значащими обозначениями. (Д. Гильберт)
Каждый сам знает, что он понимает под множеством. (Е. Борель)
Звуки умертвив,
Музыку я разъял, как труп.
Поверил я алгеброй гармонию. (А. Пушкин)
У людей, усвоивших великие принципы математики, одним органом чувств больше, чем у простых смертных. (Ч.Дарвин)
Изучение математики приближает к бессмертным богам. (Платон)
Вера и математические доказательства – две вещи несовместимые. (Ф. Достоевский)
Нет царского пути в геометрию. (Евклид)
Страх смерти обратно пропорционален хорошей жизни. (Л. Толстой).
Мы хотим внести тонкость и строгость математики во все науки, поскольку это вообще возможно; мы желаем этого не потому, что рассчитываем таким путём познавать вещи, но для того, чтобы установить этим наше человеческое отношение к вещам. Математика есть лишь средство общего и высшего человековедения. ( Ф. Ницше)
Умение решать задачи - такое же практическое искусство, как умение плавать или бегать на лыжах. Ему можно научиться только путём подражания или упражнения. ( Д. Пойа)
Математика и опыт – вот подлинные основания достоверного, естественного, разумного живого познания. (Спиноза)
Математическая истина остаётся на вечные времена, а метафизические призраки проходят, как бред больных. (Вольтер)
Правила для развития способности делать выводы …занимайся математикой. (Л. Толстой)
Очень бы я желал повторить математику; не знаю только, способен ли я теперь на это. (Л. Толстой )
Воспитывать можно только физически. Математика есть физическое воспитание. (Л. Толстой)
Геометрия является самым могущественным средством для изощрения наших умственных способностей. (Г. Галилей)
…сила речи обратно пропорциональна количеству слов. (Д. Мережковский)
…химия – правая рука физики, математика – её глаза. (М.В. Ломоносов)
…человека, умеющего наблюдать и анализировать, обмануть просто невозможно. Его выводы будут безошибочны, как теоремы Евклида. (А. Конан Дойл)
Музыка есть таинственная арифметика души; она вычисляет, сама того не подозревая. (Г. Лейбниц)
…для несведущих в математике сокрыты многие тайны вещей. (Я. Коменский)
Используйте закон больших чисел для изгнания беспокойства из вашей жизни. Спрашивайте себя: какова вероятность того, что это событие вообще произойдёт. (Д. Карнеги)
Вкусив от сладкого плода математики, мы уподобляемся лотофагам, ибо воспользова- вшись ею хоть раз, мы не хотим от неё оторваться и она овладевает нами, как цветок лотоса. (Аристотель)
Ни одна наука так не укрепляет веру в силу человеческого разума, как математика. ( Г. Штейнгауз)
В голове у Архимеда было гораздо больше воображения, чем в голове у Гомера. (Вольтер)
…поэт подобен математику, который конструирует эти отношения a priori, в чистом воззрении. (А. Шопенгауэр)
Математика лучше всего помогает нам в понимании разнообразных божественных истин. (Н. Кузанский)
Математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется и определяется вся творческая духовная деятельность человека и что между ними размещается всё, что человечество создало в области науки и искусства. ( Г. Нейгауз)
Пифагорейцы были математиками – маньяками. (А. Шопенгауэр)
“Всё, что превышает геометрию, превышает нас”, сказал Паскаль. И вследствие того написал свои философические мысли! (А. Пушкин)
Вдохновение есть расположение души к живейшему принятию впечатлений и соображению понятий, следственно и объяснению оных.
Вдохновение нужно в геометрии, как и в поэзии. (А. Пушкин)
Наука чистой математики в её современных вариантах может быть представлена в качестве самого оригинального продукта человеческого духа. (А. Уайтхед).
Силы человеческой натуры рассчитываются, словно вероятности в математике. (Казанова)
Математическое доказательство для разума непреложно. (Казанова)
Прежде чем выступать, Линкольн с математической точностью обдумывал свои выводы. Когда ему было сорок лет, и он был уже членом конгресса, он изучал Евклида, чтобы иметь возможность выявлять софизмы и доказывать свои выводы. (Д. Карнеги)
У каждого свой исходный постулат, на котором построена его геометрия жизни. Нужно только пристальнее приглядеться к человеку, определить этот исходный постулат и тогда всё станет ясно, все поступки окажутся логически обоснованными. Можно даже наперёд предсказать, как поступит тот или иной человек. (Н. Лобачевский)
Большинство жизненных задач решаются как алгебраические уравнения: приведением их к самому простому виду. (Л. Толстой)
Он дальше десятичных дробей вряд ли ходил. (П. Боборыкин)
Высшая гармония одарённого воображением интеллекта всегда наделена преимущественно математическим характером. (Э.По)
Легче сквадрировать круг, чем обойти математика. (Август де Морган)
Когда я понял, что сумма углов треугольника равняется двум прямым углам, я почувствовал в этом нечто своё, личное, бесконечно родное, чего уже никто у меня не отнимет. И среди многочисленных волнений жизни и мысли я нашёл в этом приют. Геометрия, если я её изучил и понял, моя - родная и близкая, всегда ласковая и всегда приютная наука. (А. Лосев)
Какая будет цель моей жизни в деревне в продолжение двух лет?…изучить математику, гимназический курс. (Л. Толстой, 1847г.)
Очень бы я желал повторить математику; не знаю только, способен ли я теперь на это. (Л. Толстой , 1852г).
Шеффер, математик характером – тип. (Л. Толстой)
Войска французские равномерно таяли в математически правильной прогрессии. (Л. Толстой)
Математика – это то, посредством чего люди управляют природой и собой. (А. Колмогоров)
Отчего, например, ни в одном из своих действий разум не возвышается до такой степени, как в математических исчислениях? Что такое исчисление? Умственное действие, механическая работа ума, в которой рассуждающей воле нет места. Откуда эта чудодейственная мощь анализа в математике? Дело в том, что ум здесь действует в полном подчинении данному правилу. (П. Чаадаев)
Человек научается познавать физический закон, наблюдая явления природы, которые чередуются у него перед глазами сообразно единообразному и неизменному закону. Собирая воедино наблюдения предшествующих поколений, он создаёт систему познаний, проверяемую его собственным опытом, а великое орудие исчисления облекает её в неизменную форму математической достоверности. (П. Чаадаев)
…каждая математическая теорема осущест- вляется где-нибудь в природе, в какой-либо комбинации молекул или элементов. Математика кажется нам отвлечённой только потому, что мы не замечаем применения её принципов в природе. (П. Чаадаев)
Бог нужен для метафизики, как для математики нуль. (Пестель)
Пестель…Математик глубокий; и в правоту свою верит, как в математическую истину. Везде и всегда равен себе. (Д. Мережковский)
Математика выявляет порядок, симметрию и определённость, а это – важнейшие виды прекрасного. (Аристотель)
Математик, который не является также немного поэтом, никогда не будет завершённым математиком. (К. Вейерштрасс)
...необходимо уточнение смысла терминов, а хорошую школу этого даёт математика. (А. Тоом, математик)
Математика есть прообраз красоты мира. (И. Кеплер)
Я увидел тоже математически ясно. (Н. Гоголь)
Математика – это искусство называть разные вещи одним и тем же именем. (А. Пуанкаре)
Математика нужна для изучения многих наук, но сама она не нуждается ни в какой науке. (П. Каптерев)
Для несведущих в математике сокрыты многие тайны вещей. (Я. Коменский)
У них арифметика вместо души-то. (А. Островский)
Математики – вроде французов: когда говоришь с ними, они переводят твои слова на свой язык и сразу получается что-то совсем другое (И. Гёте)
Для современного физика математика всё равно, что абсолютный слух для композитора. (Ю. Нагибин)
Математики похожи на влюблённых.…Согласитесь с математиком в самом простом высказывании, и он выведет из него следствие, с которым вы также должны согласиться, а из этого следствия – другое (Б. Фонтенель)
Математика – великое дело. (Л. Толстой)
Премудрость чисел, из наук главнейшую,
Я для людей измыслил. (Эсхил)
В его возрасте (да и всегда) есть только две науки, в пользе которых можно быть твёрдо уверенным – это язык или языки, искусство выражать и понимать всякие и во всякой форме мысли, и математика. Я бы, по крайней мере, приохочивал ребёнка только к этим двум наукам. (Л. Толстой).
Всякая хорошо решённая математическая задача доставляет умственное наслаждение. (Г. Гессе)
Вы параллельны ко всему,
А я, напротив, вертикален! (А. Толстой)
И они пускаются на поиски неизвестного с рвением учёных – математиков. (О. Бальзак)
Великий и бессмертный Спиноза … математически доказывал существование Бога. (О. Бальзак)
Когда я чувствую, что не могу больше находиться в цивилизованном обществе, я спасаюсь в чистую математику. (Б. Шоу)
Кто возьмёт на себя смелость сказать, что математическое и логическое рассуждения не страсть! (Б. Шоу)
Умение мыслить математически – одна из благороднейших способностей человека. (Б. Шоу)
Только математическая страсть не порождает реакций: наслаждение, доставляемое ею, сулит наступление такого состояния, когда жизнь будет интеллектуальным экстазом, более сильным, чем экстаз, переживаемый святыми. (Б. Шоу)
Две науки точные: математика и нравственное учение… Точны и несомненны эти науки потому, что у всех людей один и тот же разум, воспринимающий математику, и одна и та же духовная природа, воспринимающая (учение жизни) нравственное учение. (Л. Толстой)
Математика – один из видов искусства. (Н. Винер)
Математика – самый короткий путь к самостоятельному мышлению. (В. Каверин)
В истории черпаем мы мудрость, в поэзии – остроумие, в математике – проницательность. (Ф. Бэкон)
Ценность жизни обратно пропорциональна расстоянию от смерти (Л. Толстой)
Математика, правильно понятая, обладает не только истиной, но также величайшей красотой, какой обладает искусство ваяния. (Б. Рассел)
Математика для учёного – то же самое, что скальпель для анатома. (Н. Абель)
Числа не управляют миром, но показывают, как управляется мир. (И. Гёте)
Байрон оставил свою жену, которую он именовал “принцессой параллелограммов’’, ибо она была слишком проницательна и умна. (А. Моруа)
В первый раз всё изменилось для человека, когда он узнал о существовании такой науки, как математика. (А. Моруа)
Всё, что без этого было темно, сомнительно и неведомо, математика сделала ясным, верным и очевидным. (М. Ломоносов)
Высшее назначение математики как раз и состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает. (Н. Винер)
Поэзия – это разновидность вдохновенной математики, которая даёт нам уравнения, состоящие из абстрактных фигур, треугольников, сфер и тому подобному, но уравнения, служащие для выражения человеческих эмоций. (Эзра Паунд, поэт)
Математика даёт нам блестящий пример того, как далеко мы можем продвинуться в априорном знании независимо от опыта. (И. Кант)
Настоящие математические положения всегда априорные, а не эмпирические суждения. (И. Кант)
Кроме трансцендентальной философии существует ещё две науки чистого разума: одна исключительно спекулятивная, а другая исключительно практическая – чистая математика и чистая мораль. (И. Кант)
Огромные успехи, достигаемые разумом посредством математики, естественно, возбуждают надежду, что если не сама математика, то, во всяком случае её метод достигнет успеха также и вне области величин. (И. Кант)
Я бестрепетно стал за идею, ибо был математически убеждён. (Ф. Достоевский)
Он кончил совершенным и безбрежным атеизмом на основании естественных наук и математики. (Ф. Достоевский)
Никто, не познав [числа], никогда не сможет обрести истинного мнения о справедливом, прекрасном. (Платон)
Во Франции много изрядных математиков, каковые, обнаружив, что выигрыш различен для различны ставок, изыщут способ для злоупотребления. (Казанова)
Музыка, поэзия, математика – сколь родственны они. (Имре Мадач)
Математик совершенен лишь постольку, поскольку он является совершенным человеком, поскольку он ощущает в себе прекрасное, присущее истине; только тогда его творчество становится основательным, проницательным, дальнозорким, чистым, ясным, одухотворённым, действительно изящным. Всё это требуется, чтобы уподобиться Лагранжу. (И. Гёте)
Математики должны быть философами не меньше, чем философы – математиками. (Г. Лейбниц)
Я не ограничиваюсь математикой, так как истины, ею преподносимые, не должны целиком поглощать наш ум, как бы ни была велика их польза в человеческой жизни; я полагаю, что лучшее применение которое можно найти математике, состоит в том, чтобы поучиться у неё искусству строгости рассуждений. (Г. Лейбниц)
Военные, финансовые и морские дела во многом зависят от математических наук и от прикладной физики. (Г. Лейбниц)
Многие не знают математических истин не вследствие несовершенства своих способностей или недостоверности самого предмета, но вследствие недостаточного усердия в приобретении, изучении и надлежащем сравнении этих идей. (Д. Локк)
Резкая неприятная прямота допускается только у математиков, которые пробивают себе путь к истине и доставляют ей признание неопровержимыми доказательствами. (Д. Локк)
Если вы хотите, чтобы человек хорошо рассуждал, вы должны приучать его с ранних лет упражнять свой ум в изучении связи идей и в прослеживании их последовательности. Ничто не способствует этому в большей степени, чем математика, которую поэтому должны, по моему мнению, изучать все, кто имеет время и возможность, - не столько для того, чтобы сделаться математиками, сколько для того, чтобы стать разумными существами. (Д. Локк)
Пока не была открыта алгебра, это великое орудие и пример человеческой проницательности, люди с изумлением смотрели на различные доказательства математиков древности и едва ли не признавали, что открытие некоторых из этих доводов есть нечто превосходящее человеческие силы. (Д. Локк)
В нравственности доказательство возможно точно так же, как в математике. (Д. Локк)
Бог существует, поскольку математика, несомненно, непротиворечива, но существует и дьявол, поскольку доказать её непротиворечивость мы не можем. (Г. Вейль)
Математика стала для нынешних мудрецов философией, хотя они говорят, что математикой нужно заниматься ради другого. (Аристотель)
Я обнаружил огромные достоинства в составлении таких уравнений, в занятии, кое назвать позволительно будет поучительной алгеброй благоразумия. (Б. Франклин)
Математики следят за солнцем и луной, а не видят того, что у них под ногами. (Диоген)
В математике есть нечто вызывающее человеческий восторг. (Ф. Хаусдорф)
Разум есть основа и источник математики. (Д. Дефо)
Только допустив бесконечно малую единицу для наблюдения – дифференциал истории, и достигнув искусства интегрировать (брать суммы этих бесконечно малых), мы можем надеяться на постижение законов истории. (Л. Толстой)
И немногие математики будут готовы поверить, что все их построения лишь копии врождённых черт, которые природа запечатлела в их душе. (Д. Локк)
Благодаря абстрагированию мыслей от названий и привычке ставить перед своим умом сами рассматриваемые идеи, а не обозначающие их звуки математики избежали значительной части той путаницы, затруднений и неразберихи, которые так сильно мешали развитию других областей знания. (Д. Локк)
…как натыкается на прохожих поглощённый решением задачи математик… (О. Бальзак)
Заблуждаются те, кто утверждает, что математика ничего не говорит о прекрасном или благом. На самом же деле она говорит прежде всего о нём и выявляет его.…А важнейшие виды прекрасного это слаженность, соразмерность и определённость, математика больше всего и выявляет именно их. (Аристотель)
Он отнёсся к крушению, как математик к задаче, которую необходимо решить и определить неизвестное. (Ж. Верн)
Бывает это последнее время такое – минутами – ясное понимание жизни, какого никогда прежде не было. Точно сложное уравнение приведено к самому простому выражению и решению. (Л. Толстой)
Даже в математике она (фантазия) нужна, даже открытие дифференциального и интегрального исчисления невозможно было бы без фантазии. (В. Ленин)
Компьютер и сама математика – инструмент в руках исследователя, помогающий человеку найти истину. (И. Родкевич, физик)
Мысли действуют на расстояние прямо пропорционально силе, породившей их, и бьют в ту точку, куда их посылает мозг по какому-то закону математики. (О. Бальзак)
Мотив мести обратно пропорционален силе и продуктивности группы или отдельного человекаю (Э. Фромм, психолог)
Каждая теорема с доказательством тщательно переписывается на тоненькой облатке чернилами, составленными из микстуры против головной боли. Ученик глотает облатку натощак и в течение трёх дней после этого не ест ничего, кроме хлеба и воды. Когда облатка переваривается, микстура поднимается в его мозг, принося с собой туда же теорему. (Д. Свифт)
Чистая математика входит в нашу душу через посредство всех чувств. (Д. Дидро)
Математика нужна, чтобы изобретать новое огнестрельное оружие (Г. Гессе)
В эпоху, когда музыка и математика переживали классический период почти одновременно, обе дисциплины часто дружили и оплодотворяли друг друга. (Г. Гессе)
Математика. Я упомянул о математике как о способе приучить ум к точному и последовательному мышлению. Я не хотел этим сказать, что, по моему мнению, всем людям необходимо быть глубокими математиками; я лишь считаю, что, усвоив тот способ рассуждения, к которому неизбежно приобщает ум эта наука, люди способны будут переносить его в другие области знания, с которыми им придётся иметь дело. (Д. Локк)
…призадумалась было, как математик над решением трудной задачи. (И. Лажечников)
В природе существует много такого, что не может быть ни достаточно глубоко понято, ни достаточно убедительно доказано, ни достаточно умело и надёжно использовано на практике без помощи вмешательства математики. (Ф. Бэкон)
Природа – это сочетание самых простых математических идей. (А. Эйнштейн)
Мы почитаем всех нулями, а единицами себя. (А. Пушкин)
В древних Афинах считали, что кто ловко укладывает и связывает вязанки валежника, тому свойственны математические способности. (Монтень)
Количество шума, которое человек способен спокойно переносить, обратно пропорционально его духовным способностям. (А. Шопенгауэр)
Математические доказательства как алмазы, тверды и прозрачны. (Д. Локк).
Мой сын будет, наверно, математиком. Я сам любил математику, когда учился в артиллерийском училище. Математика – хороший тренинг для императора. (Наполеон, из фильма “Наполеон и Жозефина”)
Ни один человек, если он совершенно чужд математической практике, не сможет постигнуть понятий о божественных вещах. (Боэций)
Музыка есть бессознательное упражнение души в арифметике. (Г. Лейбниц)
Дорогая тётя, сообщаю вам, что я намереваюсь жениться.…Не бойтесь, она не математик. (Д. Максквел)
Математика – наука великая, замечательный продукт человеческого разума. Профанирование математики есть преступление перед разумом. (Д. Писарев)
…поэт должен только видеть то, чего не видят другие, видеть глубже других. И это же должен математик. (С. Ковалевская)
Если мы желаем сообщить уму образуемого свойство осторожного, точного мышления, и притом дедуктивного характера, то мы должны упражнять ум образуемого на серьёзном изучении математических наук. (П. Каптерев)
А для низкой жизни были числа,
Как домашний подъярёмный скот,
Потому что все оттенки смысла
Умное число передаёт. (Н. Гумилёв)
Нельзя не признать, что занятие математикой – ниспосланное богами безумие человеческого духа. (А. Уайтхед)
Вера в могущество человека отчасти зиждется на той силе, которой наделяет его математика – она помогает человеку покорять природу и тем облегчает его ношу. Одержанными математикой победами человек может по праву гордиться. (М. Клайн)
Я убеждён, что посредством чисто математических конструкций мы можем найти те понятия и закономерные связи между ними, которые дадут нам ключ к пониманию явлений природы. Опыт может подсказать нам соответствующие математические понятия, но они ни в коем случае не могут быть выведены из него. Конечно, опыт является единственным критерием пригодности математических конструкций физики. Но настоящее творческое начало присуще именно математике. (А. Эйнштейн)
Есть люди, одарённые в сильной степени нравственным и художественным чувством, и есть люди, почти лишённые его. Первые как бы сразу берут интеграл. А вторые делают сложные вычисления, не приводящие к окончательным выводам. Точно как будто первые проделали все вычисления прежде, а теперь пользуются результатами. (Л. Толстой)
…пути постигновения даже формальных, математических истин для каждого ума – свои. (Л. Толстой)
Цели художества несоизмеримы (как говорят математики) с целями социальными. (Л. Толстой)
Цель математике может дать не низшая сравнительно с ней, а высшая сфера человеческой деятельности – религия. (И.Шафаревич).
А кто рассеян, тот пусть займётся математикой, ибо при доказательстве теорем малейшая рассеянность вынуждает всё начинать сызнова. (Ф.Бэкон)
Геометрия является самым могущественным средством для изощрения наших умственных способностей и даёт нам возможность правильно мыслить и рассуждать. (Г. Галилей)
Математика владеет не только истиной, но и высшей красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства. (Б. Рассел)
…всякая оценка есть произведение из достоинства ценимого на духовные способности ценителя. (А. Шопенгауэр)
Невозможно проверить алгеброй гармонию и невозможно проверить – т.е. познать – гармонию без алгебры (О. Каган, скрипач)
Мне хочется, чтобы живописец был как можно больше сведущ во всех свободных искусствах, но прежде всего я желаю, чтобы он узнал геометрию. (А. Альберти)
Истина должна быть проверена опытом, а по возможности и приложением математических методов. (П. Лесгафт)
Математика преследует троякую цель. Она должна давать орудие для изучения природы. Кроме этого она преследует цель философскую, и - я решаюсь сказать – эстетическую…
Математика должна помогать философу углубляться в понятие числа, пространства и времени. Люди, посвящённые в её тайны, вкушают наслаждения, подобные тем, которые даёт нам живопись и музыка.
(А. Пуанкаре)
…без мечты нет и математики. (Гюго)
Только геометр и глупец говорят, не прибегая к образной речи. (Руссо)
Из всех наук высшая математика – самая фантастическая, можно сказать, поистине божественная по своей природе. (Казанова)
Просмотр содержимого документа
«chasi»
С  олнечные часы.
олнечные часы.
Самые первые часы на земле - солнечные.
Они были гениально простыми: воткнутый в землю шест. Вокруг него нарисована шкала времени. Тень от шеста, передвигаясь по ней, показывала, который сейчас час. Позднее такие часы делали из дерева или камня и устанавливали на стенах общественных зданий.
Затем появились переносные солнечные часы, которые изготавливали из ценных пород дерева, слоновой кости или бронзы.

Были даже часы, которые условно можно назвать карманными; их нашли при раскопках древнего города. Эти солнечные часики, сделанные из посеребренной меди, имели форму окорока, на котором прочерчены линии. Шпилем - стрелкой часов - служил свиной хвостик. Часы были небольшие. Их вполне можно было бы поместить в кармане. Но карманов жители древнего города еще не придумали. Вот и носили такие часы на шнурке, цепочке или прикрепляли к тросточкам из дорогого дерева.
Первый простейший прибор для измерения времени — солнечные часы — был изобретен вавилонянами примерно 3,5 тысячи лет назад. На плоском (кадран), разграфленном линиями, камне, служившим циферблатом, укрепляли небольшой стержень (гномон), а часовой стрелкой служила тень от него. Время по таким часам можно было узнавать только днем, поэтому ночью им на замену приходили водяные часы, названные греками клепсидра. Металлический, глиняный или стеклянный сосуд наполняли водой, которая медленно, по капле, вытекала, уровень ее понижался, и по делениям на сосуде определяли который час. Не менее распространенными в Европе и Китае были так называемые «огненные» часы — в виде свечей с нанесенными на них делениями.
Солнечные часы имели один существенный недостаток: они могли «ходить» только на улице, да и то на освещенной солнцем стороне. Это, конечно, было крайне неудобно. Видимо, поэтому изобрели водяные часы.
Водяные часы
 По капелькам вода перетекала из одного сосуда в другой, и по тому, сколько воды вытекало, определяли, сколько прошло времени. Водяные часы - `клепсидры` - были известны уже египтянам и некоторым культурным народам Дальнего Востока. Их наименование происходит от сочетания двух греческих слов klepto – брать и udor - вода. В Китае, например, ими пользовались 4,5 тысячи лет назад. Кстати, первый будильник на земле тоже был водяным - и будильником, и школьным звонком одновременно. Его изобретателем считают древнегреческого философа Платона, жившего за 400 лет до нашей эры. Этот прибор, придуманный Платоном для созыва своих учеников на занятия, состоял из двух сосудов. В верхний наливалась вода, откуда она понемногу вытекала в нижний, вытесняя оттуда воздух. Воздух по трубке устремлялся к флейте, и она начинала звучать. Причем будильник регулировался в зависимости от времени года.
По капелькам вода перетекала из одного сосуда в другой, и по тому, сколько воды вытекало, определяли, сколько прошло времени. Водяные часы - `клепсидры` - были известны уже египтянам и некоторым культурным народам Дальнего Востока. Их наименование происходит от сочетания двух греческих слов klepto – брать и udor - вода. В Китае, например, ими пользовались 4,5 тысячи лет назад. Кстати, первый будильник на земле тоже был водяным - и будильником, и школьным звонком одновременно. Его изобретателем считают древнегреческого философа Платона, жившего за 400 лет до нашей эры. Этот прибор, придуманный Платоном для созыва своих учеников на занятия, состоял из двух сосудов. В верхний наливалась вода, откуда она понемногу вытекала в нижний, вытесняя оттуда воздух. Воздух по трубке устремлялся к флейте, и она начинала звучать. Причем будильник регулировался в зависимости от времени года.
Клепсидры были очень распространены в древнем мире.
Кроме водяных часов были известны еще часы песочные и огневые (чаще всего будильники). На Востоке последние представляли собой палочки или шнуры, сделанные из медленно горящего состава.
Песочные часы.
Первые песочные часы появились более тысячи лет назад. При помощи этих часов можно было измерять лишь небольшие промежутки времени, обычно не более получаса.

Особенно большое значение имели песочные часы на кораблях: в пасмурную погоду, когда по небесным светилам нельзя было определить время, его узнавали по песочным часам. А в конце XVI века было сделано новое открытие. Молодой ученый Галилео Галилей, наблюдая за движением самых разных лампад в Пизанском соборе во время богослужения, установил, что ни вес, ни форма лампад, а лишь длина цепей, на которых они подвешены, определяет периоды их колебаний от ветра, врывающегося в окна. Ему и принадлежит идея создания часов с маятником.
Механические часы.
Знаменитый голландский ученый Христиан Гюйгенс в 1656г. создал довольно совершенные механические часы с маятником.
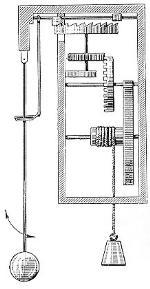
В этих часах гиря поворачивала колесо, и его вращение передавалось верхнему - храповидному колесу. Маятник проходил между зубьями вилки, и при каждом качании вилка заставляла поворачивать то вправо, то влево стержень с двумя пластинками. Эти пластинки были расположены так, что поочередно упирались то в один, то в другой зубец храповидного колеса.
Теперь в механических часах маятник и груз, какие были в громоздких напольных часах, заменили тоненькие витки пружин. Пружины приводят механизм в действие и регулируют скорость вращения шестеренок, двигающих стрелки. Современные пружинные часы – одно из самых точных механических устройств, когда либо, созданных человеком.
Конструкция часов
Первые механические часы имели лишь одну часовую стрелку и грубый немецкий или итальянский (древнечешский) циферблат, т.е. с 12-часовой или 24-часовой шкалой.
У однострелочных часов на циферблате преобладали гравированные римские цифры. У напольных часов с квадратным латунным циферблатом мы часто встречаемся со шкалой, выгравированной в самом латунном кольце, прикрепленном к некруглой циферблатной плите. Видимые части циферблатной плиты вокруг кольца украшались гравированными орнаментами или же литыми латунными рельефными аппликациями, расположенными прежде всего в углах циферблата.


С маятниковыми часами пришла в хронометрию повышенная точность измерения времени, а с этим появилась и минутная стрелка на циферблате. Для этой стрелки изготовляли и специальную минутную шкалу, расположенную на внешней окружности прежней часовой шкалы.
Для обозначения пятиминутных интервалов на этой шкале сначала служили лишь арабские цифры, которые у небольших циферблатов были по соображениям экономии пространства непосредственно частями шкалы, а у больших часов их выгравировывали или рисовали над часовой шкалой.
Интересны изменения формы стрелок. У однострелочных часов стрелки надевались на четырехгранный часовой вал, а для облегчения проворачивания их рукой они имели на противоположном удлиненном конце носик или опору для пальца.
Во второй половине XVIII в., когда у часов стали встречаться все чаще неразборные серебряные или посеребренные циферблаты, часовщики стали делать часовые и минутные стрелки одинаковой формы, но различающиеся по величине. Многие изобретатели старались усовершенствовать часы, и в конце XIX века они стали вещью обыденной и необходимой. Очередная революция в способах измерения времени произошла в конце 60 годов – с изобретением кварцевых часов. Кварц обычный минерал, довольно распространенный. Если через него пропустить от батарейки ток небольшого напряжения, кварц начинает вибрировать со строго определенной частотой. Микросхемы, подобные компьютерным, подсчитывают количество колебаний и показывают время на циферблате. Такие часы могут иметь цифровой дисплей, который в отличие от механических показывает время одними цифрами, без стрелок. Их циферблат сделан из жидких кристаллов. Атомные часы отличаются невероятной точностью, они идут с погрешностью лишь в одну секунду, за два или три миллиона лет! Атомные часы основаны на высвобождении энергии в результате процессов происходящих в атоме.

Интересно о часах.
* 1485 год. Леонардо да Винчи сделал эскиз устройства fusee для башенных часов. Как выяснилось, карманные часы от башенных отличаются только размерами - принцип тот же.
* Часы, в основе работы которых лежит механизм с колеблющимся маятником, создал голландец Христиан Гюйгенс. Однако это стало возможным благодаря экспериментам и исследованиям, проводимым знаменитым математиком и астрономом Галилео Галилеем в 1580-м году.
* Изобретение маятника примерно в начале 15-го века способствовало появлению и первых домашних часов, которые изготавливали местные кузнецы и мастера. Первое время домашние часы вешались на стену, поскольку их маятники были действительно огромными. С дальнейшим усовершенствованием часовых механизмов часы становились все легче и компактнее, и вскоре была создан их настольный вариант.
* Благодаря изобретению Галилея, погрешность измерения времени снизилась с 20-30 минут в день до 3 минут, а изобретение анкерного механизма позволило снизить эту погрешность до 3 с в неделю , что считалось большой точностью.
* Для производства механических часов, какими были первые образцы, требовались гораздо более точные станки, чем весь прежний инструментарий. Современное точное машиностроение родилось из мастерства механиков часовщиков.
* Самая ранняя дата, которую можно достоверно назвать, говоря о применении шпиндельных механических часов, относится приблизительно к 1340 г. или несколько позже (с точностью до нескольких лет). С тех пор они быстро вошли в общее употребление и стали предметом гордости городов и соборов. В 1450 г. появились пружинные часы, а к концу XV столетия — переносные часы, но еще слишком крупные, чтобы их можно было назвать карманными или наручными.
Просмотр содержимого документа
«chisla_raskazut»
ЧИСЛА РАССКАЖУТ О СЕБЕ

Число – одно из основных понятий математики, позволяющее выразить результаты счета или измерения. Понятие числа служит исходным для многих математических теорий. Числа находят широкое применение В физике, механике, астрономии, химии и многих других науках. Числами постоянно пользуются в повседневной жизни.
В школьном курсе мы будем постепенно знакомиться со всеми числами, в том числе с натуральными, действительными, рациональными и иррацинальными. Но в данной работе мы будем говорить о мало знакомых нам числам, а именно совершенных, дружественных и фигурных числах.
Согласно учению Пифагора, числа являются мистической сущностью вещей, математические абстракции таинственно руководят миром, устанавливая в нем определенный порядок. Пифагорейцы высказывали предположение о том, что все закономерности мира можно выразить с помощью чисел. Числа признавались не просто выражениями закономерного порядка, но и основой материального мира.
Сами пифагорейцы высоко ценили результаты, полученные ими в теории гармонии, ибо они подтверждали их идею, что числа определяют все. Число для пифагорейцев – это собрание единиц (только целое положительное число). Единицы, составляющие число, считались неделимыми и изображались точками, которые располагались в виде правильных геометрических тел. При этом получали ряды «треугольных», «квадратных», «пятиугольных» и других «фигурных» чисел. Одинаковые шары можно укладывать на плоскости так, чтобы они образовывали различные фигуры – треугольники, квадраты, шестиугольники и т. д.
«Треугольные» числа это числа 1; 1+2=3; 1+2+3=6; 1+2+3+4=10, общее выражение для них 1+ 2+ 3+…+![]() =
=![]() .
.
Рассмотрим «упаковки» шаров в равностороннем треугольнике. Числа, которые показывают, сколько шаров содержится в треугольниках, называют треугольными.
«Квадратные» числа это числа 1; 1+3=4; 1+3+5=9; 1+3+5+7=16; …; 1+3+5+…![]() .
.
Пифагорейцы определили также «кубические» числа 1; 8; 27;…. Отметим, что наши выражения «квадрат» для числа ![]() и куб для числа
и куб для числа ![]() являются пережитком пифагорейской терминологии.
являются пережитком пифагорейской терминологии.
Пифагорейцы рассматривали «пятиугольные» числа 1; 1+4=5; 1+4+7=12; 1+4+7+…+![]()
Совершенным числом называют натуральное число, равное сумме всех его собственных деталей, т.е. делителей, отличных от самого числа. Так, совершенными числами являются числа 6 и 28, ибо 6=1+2+3, 28=1+2+4+7+14.
Знаменитый греческий философ и математик Никомах Герасский, живший в 1 в., отмечал, что совершенные числа красивы, а красивые вещи редки и немногочисленны. Он не знал, сколько имеется совершенных чисел. Не знаем этого и мы. До настоящего времени нет ответов на два важных вопроса:
1) Существует ли наибольшее чётное совершенное число?
2) Существует ли нечетное совершенное число?
До сегодняшнего дня не обнаружено ни одного нечетного совершенного числа, хотя и не доказано, что такого числа не существует. Было обнаружено правило, как искать четные совершенные числа. Это правило состоит в следующем: если число ![]() простое, то число
простое, то число ![]() совершенное.
совершенное.
Все совершенное редко встречается в мире. Редко встречаются и совершенные числа. Пара натуральных чисел называется дружественной, если каждое из них равно сумме всех собственных делителей другого. Например, дружественную пару образует числа 220 и 284, так число 220 имеет делители 1,2,4,5,10,11,20,22,44,55 и 110, а число 284 – делители 1,2,4,71,142 и выполняются следующие равенства:1+2+4+5+10+11+20+22+44+55+110=284 1+2+4+71+142=220
Все известные дружественные пары состоят либо из двух четных чисел, либо
из двух нечетных. До сих пор не обнаружено дружественной смешанной пары, но вместе с тем и не доказано, что такой пары не существует. Неизвестно также, конечно или бесконечно число дружественных пар.
Приведём краткие сведения из интересной истории совершенных чисел и дружественных пар чисел.
Первых прекрасным совершенным числом, о котором знали математики Древней Греции, было число 6. Этому числу уделяли много внимания математике, философы, богословы. В библейских преданиях утверждается, что мир был создан в шесть дней; ведь более совершенного числа среди совершенных чисел, чем 6, нет, так как оно первое из них, Следующим совершенным числом, известным древним грекам до Евклида, было число 28. Евклид сделал первый важный шаг в построение теории совершенных чисел. Он доказал, что всякое число, которое может быть представлено в виде произведения множителей 2p-1 и 2p-1, где 2p-1 простое число, является совершенным числом. Отметим, что для этого необходимо, чтобы p было простым, хотя далеко не для всякого простого числа p число 2p-1 также является простым.
В течение почти двух тысяч лет люди знали только четыре совершенных числа. Неизвестно было, существуют ли другие совершенные числа, которые можно представить в виде 2, и возможны ли совершенные числа, не удовлетворяющие этой формуле. Неразрешимая загадка совершенных чисел, бессилие разума перед их тайной привели к признанию божественности этих удивительных чисел. Церковь учила, что для спасения души достаточно изучать совершенные числа; тому, кто найдёт новое божественное совершенное число, уготовано вечное блаженство. Но даже надежда на такую награду не смогла помочь математикам средневековья. Лишь в ХV в. было обнаружено пятое совершенное число. Им оказалось число 33550336, его можно получить по формуле Евклида при p = 13.
Через двести лет усиленными поисками новых совершенных чисел занялся французский физик, математик и богослов Марен Мерсенн. Он утверждал, что следующие шесть совершенных чисел должны иметь евклидовскую форму со значениями p, равными 17, 19, 31, 67, 127, 257. Долгое время оставалось неизвестным, прав был Мерсенн или нет. Оказалось, что не все утверждения Мерсенна были верны. Он правильно предсказал значения p = 17, p = 19, p = 31, p = 127. Числа, полученные по формуле Евклида 2 при p = 67 и при p = 257, вопреки Мерсенну, не являются совершенными. Мерсенн «пропустил» совершенные числа со значениями p = 61, p = 89, p = 107. Всё это было обнаружено позже.
Л. Эйлер сумел найти новую теорему о таинственных и загадочных совершенных числах: все чётные совершенные числа имеют вид, указанный Евклидом. Вопрос о том, существуют ли нечётные совершенные числа и каков их вид, остаётся открытым до нашего времени. И.М. Первушин нашёл девятое совершенное число – 2305843009213693951![]() , которое содержит тридцать семь цифр. Он совершил при этом настоящий вычислительный подвиг, так как считал без всяких вычислительных средств. Мерсенн в своё время заметил, что вечности не хватит для проверки простоты числа, имеющего 15-20 знаков (простое число Первушина имеет 19 знаков). Последующие совершенные числа находили с помощью вычислительных устройств, включая ЭВМ. В настоящее время известно 23 совершенных числа; последние пять чисел получаются по формуле Евклида соответственно при p = 4253, p = 4423, p = 9689, p = 9941 и p = 11213. Число 2 (2- 1) имеет 2561 знак, а число 2 (2 - 1) – 6751 знак.
, которое содержит тридцать семь цифр. Он совершил при этом настоящий вычислительный подвиг, так как считал без всяких вычислительных средств. Мерсенн в своё время заметил, что вечности не хватит для проверки простоты числа, имеющего 15-20 знаков (простое число Первушина имеет 19 знаков). Последующие совершенные числа находили с помощью вычислительных устройств, включая ЭВМ. В настоящее время известно 23 совершенных числа; последние пять чисел получаются по формуле Евклида соответственно при p = 4253, p = 4423, p = 9689, p = 9941 и p = 11213. Число 2 (2- 1) имеет 2561 знак, а число 2 (2 - 1) – 6751 знак.
Совершенные числа обладают рядом таинственных и вместе с тем замечательных свойств. Все эти числа являются «треугольными» (о таких числах говорилось выше). Каждое совершенное число есть сумма вида 1 + 2 + 3 + … + n. Далее, любое совершенное число, кроме 6, есть частичная сумма ряда из кубов нечётных чисел, т. е. равно 1 + 3 + 5 + … + (2k – 1) . Сумма обратных значений всех делителей совершенного числа, включая и само число, всегда равна 2. Например, для числа 28 имеем: ![]()
Дружественные пары чисел являются обобщением совершенных чисел. Наименьшая дружественная пара чисел 220 и 284 была известна древним грекам. В 1636г. Пьер Ферма указал новую дружественную пару чисел: 17296 и 18146. Рене Декарт нашёл третью дружественную пару чисел: 9363584 и 9437056. Ферма и Декарт независимо друг от друга установили правило образования дружественных пар чисел. Леонард Эйлер опубликовал список 64 дружественных пар. Позже было обнаружено, что в двух случаях он ошибся. В 1830г. Лежандр нашёл ещё одну дружественную пару чисел. В 1867г. шестнадцатилетний итальянец Б. И. Паганини удивил математический мир своим сообщением о том, что числа 1184 и 1210 образуют дружественную пару. Это вторая по величине дружественная пара, однако её не заметили учёные, интересовавшиеся данным вопросом.
В настоящее время известно более 600 дружественных пар чисел, большинство из них найдено с помощью ЭВМ. Многие числа дружественных пар состоят более чем из 30 цифр.
Приведём некоторые примеры дружественных пар чисел: 2620 и 2924, 5020 и 5564, 6232 и 6363, 10744 и 10856, 12 285 и 14 595, 63020 и 76 084, 66928 и 66992, 67095 и 71145, 69615 и 87633.
Существуют еще числа близнецы. Два простых числа, разность которых равна 2, называются близнецами. Ученые до сих пор не знают, есть ли самая большая пара чисел-близнецов.
Мистические свойства некоторых чисел.
Магические свойства чисел волновали людей еще в глубокой древности. Хотим мы этого или нет, но где-то глубоко в нас сидит какая-то симпатия к одним числам и осторожность , а порой и совсем неприятные чувства к другим. Особым почитанием окружены были числа в Древней Греции. Философ и математик Пифагор утверждал, что «числа правят миром». Он создал школу единомышленников, которые верили в магию чисел и думали, что за каждым предметом стоит какое-то число. Числа, считали они, несут с собой добро и зло, счастье и несчастье.
Число 0. Это символ абсолюта, бесконечности и является числом непроявленного мира. Это начало всех вещей, это сон или смерть. Графически изображается как кольцо или круг.
Единица. Пифагор и его единомышленники ставили единицу выше всех других чисел, считая, что именно она – начало всех начал, что именно от нее пошел весь мир. Без единицы не состоялось бы самое простое счисление. Графически изображается как вертикальная линия.
Двойка. Это число является символом любви, непостоянства и равновесия. Число 2 – это мягкость и тактичность, стремление сгладить острые углы. Оно находится между добром и злом, теплом и холодом, светом и мраком, богатством и нищетой.
Тройка. У многих народов весьма продолжительное время пределом счета было число 3. Его считали символом полноты, совершенства. Так, у древних греков это число считалось счастливым, а в Древнем Вавилоне стали поклоняться трем божествам: Солнцу, Луне и Венере. Число три стало самым излюбленным числом и в мифах, и в сказках. Еще его магия заключалась в том, что оно складывалось из суммы предыдущих чисел (3=1+2), символизировалось треугольником, который представляет прошлое, настоящее и будущее.
Четвёрка. Древние считали это число символом устойчивости и прочности. Ведь оно представлено квадратом, четыре стороны которого означают четыре стороны света, четыре времени года, четыре стихии- Огонь, Земля, Воздух и Воду.
Геометрическая правильность: квадрат или ромб; в славянской символике - символ Земли.
Тоже очень знаменательное число, как и три.
В японо-китайском мире 4-роковое число.
Числу 5 Пифагор отводил особое место, считая его самым счастливым из всех чисел. Древние же считали число «пять» символом риска, приписывали ему непредсказуемость, энергичность и независимость.
Числовая правильность: 5-простое число; 5 пальцев - пятеричная система счисление; 5- конечная звезда; 5 чувств ( зрение, слух, обоняние, осязание, равновесие). 5 главных признаков в православие: Обрезание Господне, Рождество Иоанна, Праздник святых Петра и Павла, Усекновение главы Иоанна-Крестителя, Покров пресвятой Богородицы. 5 заветов буддизма; мусульманин молится 5 раз в день.
Число 6. Неужели и о нём можно что-то порассказать? Конечно. Пифагор считал его удивительным числом, так как оно обладает замечательным свойством: получается в результате сложения или перемножения всех чисел, на которые делится. Шестёрка делится на 1, 2, 3 и если сложить или перемножить эти числа, то вновь получиться 6 (1 + 2 + 3 = 1 х 2 х 3 = 6). Таким свойством не обладает ни одно другое число.
6 - «число творения», Бог создал мир за 6 дней.
Геометрическая правильность: правильная, плоская, выпуклая фигура – правильный 6 - угольник.
В славянской символике – символ солнца.
Числовая правильность: 6 – совершенное число.
6 – число предметов в чайных и столовых сервизах.
Семь. В египетской и вавилонской философии и астрономии оно рассматривалось как сумма двух «жизненных» чисел: три и четыре. Три человека – отец, мать, ребёнок составляют основу жизни; а четыре – это число стран света и направлений ветра, откуда приходит дождь, живительная влага которого делает землю плодоносящей. По утверждению Пифагора, сумма чисел 3 и 4 (символизирующих собой треугольник и квадрат) считалось проявлением законченности и совершенства. Поэтому-то число 7, сумма тройки и четвёрки, воспринималось как священное.
Семь считали магическим, возможно, ещё и потому, что человек воспринимает окружающий мир (свет, звуки, запахи, вкус) через семь «отверстий» в голове (два глаза, два уха, две ноздри, рот).
Свято почитали число и древние евреи. В Священном писании говорится: «…В шесть дней создал Господь небо и землю, море и всё, что в них, а в день седьмой почил». С тех пор евреи, а затем и все христиане, воспринявшие от них Ветхий Завет, считают 7 священным числом.
С давних пор число 7 имело разное символическое значение. Так, древние греки ежегодно выбирали 7 лучших актёров (комических и трагических), древние римляне почитали семерых мудрецов.
В христианстве говориться о семи грехах и семи таинствах. У мусульман местом «высшего просветления» считается седьмое небо, куда, якобы, попадают все угодные аллаху.
Это волшебное число широко использовалось в сказках, мифах древнего мира. У Атланта, подпиравшего плечами небесный свод, было семь дочерей-плеяд, которых Зевс превратил потом в созвездия. Одиссей семь лет был в плену у нимфы Калипсо. У вавилонян подземное царство окружено семью стенами. Будда сидел под фиговым деревом с семью плодами. У индусов есть обычай дарить на счастье семь слоников. Великий пост у христиан длиться семь недель. В Библии повествуется о семи светильниках, семи ангелах, о семи годах изобилия и семи - голода.
Сказки и загадочное число семь: злодей Синяя Борода имел семь жён; семь путешествий Синбада; Белоснежка жила у семи гномов за семью горами; волк и семеро козлят; семеро из одного стручка; храбрый портняжка убил семь мух одним ударом; царевна жила в лесном тереме у семи богатырей; цветик - семицветик и др.
Христос: 7 страстей, страстная неделя.
У японцев: 7 добрых богов; на веку человека случается 7 удач.
А вообще-то особой геометрической правильностью семёрка не обладает, да и очень неудобное для расчётов это число, но испокон веков почиталось оно как священное число.
Число 8. Древние считали воплощением надежности, доведенным до совершенства. Символизировалось двойным квадратом. Разделенное пополам, оно имеет равные части. Если его еще разделить, то части тоже будут равными(2, 2, 2, 2).
Девятка. Таинственную силу приписывали древние и числу 9, причем в одни времена добрую, в другие – злую.
У древних римлян за этим числом установилась добрая слава. Монголы считали девятку совершенством. В японо-китайском мире 9 – несчастливое число; воспринимается как «болезнь».
Десять. Символом гармонии и полноты выступало число 10. Этим числом, выражающимся суммой 1+2+3+4, символизировался философский камень. Десяток стал основой десятичной системы счета, которую используют во всем мире.
Одиннадцать. Наши предки относили к нехорошим числам, число 11. Как теперь установлено, изменения активности Солнца влияют на здоровье людей, а такие изменения совершаются периодически через каждые 11 лет. Но это совсем не значит, что число 11 имеет мистическое значение.
Число 12. Очень почиталось число 12, «дюжина». 12 месяцев в году, 12 знаков Зодиака, 12 делений на циферблатах часов, сервизы на 12 персон. Число 12 замыкало свет, поэтому его считали символом полноты, богатства, счастливым числом. Число 12 имеет собственные делители 2, 3, 4, 6, что при низком уровне вычислений в древности давало большие преимущества.
Число 13. А вот с числом 13 были одни неприятности. Оно простое и делится только на себя и единицу. Суеверия, связанные с числом 13, оказались наиболее устойчивыми и получили наибольшее распространение. Люди многих стран(Англия, Франция, Польша и др.) считают это число несчастливым, испытывают перед ним панический страх и стараются избегать его. Но интересно заметить, что у наших предков – славян не было суеверий, связанных с числом 13.
Число 40. Оно играет в преданиях многих восточных народов особую роль. Выступая на определенной стадии предельным при счете, число 40 попадает в категорию счастливых. С числом 40 связан ряд религиозных обычаев и народных поверий.
Число 60. Во многих вавилонских, персидских и греческих легендах синонимом самого большого представлялось 60. Это число вавилоняне считали «божьим».
Число 1001. Это число считалось мистическим. Получается оно последовательным умножением трех простых чисел: 7, 11 и 13. А если умножить на него любое трехзначное число, то результат будет состоять из умноженного числа, записанного дважды.
Число 666. Число 666- число зверя. В разных странах христиане обозначали этим числом неугодных церкви правителей, общественных деятелей, выдавая их за антихристов.
Число 3
В далекие времена люди с большим трудом научились считать сначала до двух и только через много – много лет начали продвигаться в счете. Каждый раз за двойкой начиналось что-то неизвестное, загадочное. Когда считали “один, два, много”, то после двух было “всё”. Поэтому число три, которое при счёте должно было идти за числом два, обозначало “всё”.
Числа – это выражение определённого количества. У всех народов существовал только ручной счет: тройку показывали тремя пальцами. А если надо было записать числа, пальцы заменялись палочками. Какое число, столько и палочек. Иногда их располагали лёжа, порой – стоя. Римские цифры, которые особенно похожи на ручной палочный счет, так и писались – стоя: I, II, III. А в нынешних цифрах, что пришли к нам от арабов, стоит, словно вытянутый палец, только единица, остальные улеглись набок. Тройка – это лежащие палочки с двумя косыми росчерками ![]() .
.
Писались цифры по-разному. Вот как писали цифру три:
-
в Месопотамии

-
в Египте
-
в Вавилоне
-
у народов Майя
-
древние славяне для записи цифр пользовались буквами алфавита со специальными черточками наверху. Такая черточка называлась “титло”

-
арабская 3.
Цифру три можно изобразить с помощью набора пяти отрезков ![]() или четырех отрезков
или четырех отрезков ![]() . Эти цифры предназначены для электронных машин и используются на почтовых конвертах.
. Эти цифры предназначены для электронных машин и используются на почтовых конвертах.
Число три считалось в древности магическим, потому что оно складывалось из суммы двух предыдущих (3 = 2 + 1), символизировало треугольник, который представляет прошлое, настоящее и будущее. Даже в начале XX века жители некоторых островов Полинезии считали предметы так: один, два, три, много. Пифагорейцы разбили числа на четные и нечетные. Четные числа считались мужскими, а нечетные – женскими. Одни числа считали счастливыми, а другие – несчастливыми, несущими зло и горе. От Пифагора и его последователей и пошли всякие суеверия, связанные с числами. Особенно много суеверий связано с числом три. Те, кто считает его счастливым, говорят: “Бог троицу любит”. Другие напротив, считают его несчастливым. Отсюда и ругательное слово “треклятый”. Число три играло важную роль в магических обрядах. Все заговоры для придания им большей силы должны были произноситься трижды. От сглаза трижды плюют через левое плечо и трижды стучат по дереву. А троекратный поцелуй по русскому обычаю? В различных поверьях и легендах сохранились триединые действия: скажем, успех достигался с третьего раза (с третьей попытки). Особенно в спорте. Три попытки попасть в кольцо, полагая, что этого достаточно.
Легенды тоже не избежали числа три. Например, сказание о том, что Земля держится на трех китах. Дух триединства проявляет себя везде и во всем. Смотрите сами:
-
составляющие времени: прошлое – настоящее – будущее;
-
трехмерность пространства: высота – ширина – длина;
-
три ветви жизни: животные – растения – микроорганизмы;
-
три исторические эпохи: современная – средние века – древний мир;
-
три периода жизни человека: молодость – зрелость – старость;
-
человек имеет три основные силы: мыслительную – эмоциональную – двигательную;
-
человеку свойственны три проявления ума: интуиция – интеллект – инстинкт;
-
продолжительность жизни на земле: мужское начало – женское начало – новая жизнь.
И, наконец, последний пример: Земля – третья по расстоянию от Солнца планета Солнечной системы. Да, магическая это цифра – три!
Число три стало самым излюбленным числом и в мифах, и в сказках. Вот яркие примеры: камень на распутье предлагает богатырю три пути, отправляют за тридевять земель, в тридесятое государство, у отца три сына или три дочери, золотая рыбка и джинн выполняют по три желания, на третий раз обычно всё получается, «три девицы под окном…», три головы у Змея Горыныча, три стрелы Ивана-царевича в сказке «Царевна-лягушка» - всё это подтверждения моим словам. Можно вспомнить и названия сказок, фильмов, пьес. К примеру: три богатыря, три медведя, три мушкетёра, три толстяка, три танкиста, три сестры.
Как же не задуматься о таком совпадении!? То, что везде используют число три (реже – семь и одиннадцать), я заметил давно. А про простые числа (а главное про их свойства) совсем недавно. Вспомним свойства простых чисел. Они делятся только на единицу и на самих себя. Соответственно являются самыми «крепкими» числами при делении. Не зря поросята (из сказки «Три поросёнка») были чуть-чуть не съедены когда остались по одному. А «победили» волка лишь когда снова оказались вместе.
Три богатыря земли русской, трехглавый дракон, в тридевятом царстве, в тридесятом государстве. А где оно? Оказывается, рядом, потому что 3 х 9 = 27, 27 дней – это как раз лунный месяц – время обращения Луны вокруг Земли. Идем дальше: 3 х 10 = 30, а это период между двумя новолуниями. Вот вам и указание на то, где находится “Тридевятое царство, Тридесятое государство” – на расстоянии, равном месяцу пути.
Вот такой пример сказочной математики.
Едва ли не в каждой сказке появляется цифра три. Вот несколько названий:
-
“Три медведя”
-
“Три арбузных семечка”
-
“Три калача и одна баранка”
-
“Три толстяка”
-
“Три ветра”
-
“Три поросенка”
-
“Три подземных царства”
-
“Три товарища”
-
“Три брата”
-
“Три счастливца”
-
“Три смерти”
-
“Три очка за старичка”
-
“Три мушкетера”
-
“Три охотника”
-
“Трое умельцев”
-
“Три царевича”
-
“Три встречи”
-
“Третий глаз Шивы”
-
“Три друга”
-
“Три богатыря” и другие. Их много.
По мнению русских три приносит людям счастье. Любовь русских людей к цифре три имеет дело с христианской и греческой культурой. В «Библии» много сказок о числе три: У израильтян есть трое святых предков. Иисус ожил через три дня после смерти . Троица имеет в виду триединое божество, то есть бог-отец, бог-сын, бог-дух святой. По обычаю, когда встречаются русские люди, то они целуются трижды. В русском языке во многих поговорках и пословиц употребляют цифру три.
ПОСЛОВИЦЫ И ПОГОВОРКИ, СОДЕРЖАЩИЕ ЧИСЛО 3.
1. Три раза прости, а в четвёртый прихвостни.
2. Три деньги в день, куда хочешь, туда и день.
3. Три дни молол, а в полтора дни съел.
4. Три попа, а заросла в церковь тропа.
5. Три беды, семь бед, а всё помощи нет.
6. Трёх лет Ивана по отечеству звать рано.
7. Три дня – не три года.
8. За учёного трёх неучёных дают, да и то не берут.
9. Говорит три дня, а всё про злыдни.
10. Наскочил плут на тройного плута.
11. От горшка три вершка.
12. Наврал с три короба.
13. Заблудился в трех соснах.
14. Мнится – писание лёгкое дело: пишут три перста, а болит всё тело.
15. В августе мужику три заботы: и косить, и пахать, и сеять.
16. Февраль три часа прибавит.
17. Заведутся злыдни на три дня, и не изживёшь довеку.
18. В лес идут на троих один топор берут.
19. Не хвались замужеством третьего дня, а хвались третьего года.
20. В нашей волости три болезни: рекрутство, подати да земщина.
21. На то лето, не на лето, а на третий год, когда чёрт пошлёт.
ЧИСЛО 3 В РЕЛИГИИ
Для начала обратимся к христианству. Самое известное - это Святая Троица: Бог-Отец, Бог-Сын и Святой Дух. Три волхва принесли дары родившемуся Иисусу в Назарет. Согласно Новому Завету три дня и три ночи надлежало быть Сыну Божьему в сердце земли; Иисус Христос воскрес утром на третий день; Трижды отрёкся от Иисуса апостол Пётр. Идея триединства составляет основу многих философских и религиозных учений. В Древнем Вавилоне поклонялись трем главным божествам: Солнцу, Луне, Венере. В Индии поклоняются трехглавому Тримурти. На Востоке этот принцип назывался “Сам-цей” – “Три драгоценности”. Высочайшая драгоценность внизу – это Земля, высочайшая драгоценность в середине – это Небо, высочайшая драгоценность в середине – это Человек. В славянской мифологии 3 — одна из трёх священных цифр. Обозначает: 1) количество священных цифр; 2) троичность миросозидания (трансцентдентные сущности Тригла и Триглав). Имеет своё изображение в магических и народных орнаментах.
ЧИСЛО 3 В СКАЗКАХ А. С. ПУШКИНА
Очень интересовался происхождением арабских цифр наш великий поэт и сказочник Александр Сергеевич Пушкин. Он думал, что все арабские цифры могли получиться из квадрата, пересеченного диагоналями.
А вот сделанная им запись:
ABECD – цифра 3;
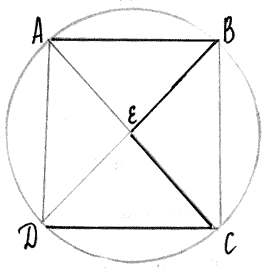
AD – цифра 1;
ABDC – цифра 2;
ABD + AE – цифра 4.
В сказках Пушкина уже в зачине часто встречается цифра три. Например:
-
“Негде, в тридевятом царстве, в тридесятом государстве, жил-был славный царь Дадон…”
-
“Три девицы под окном пряли поздно вечерком…”
-
“Жил старик со своею старухой у самого синего моря.
-
Они жили в ветхой землянке ровно тридцать лет и три года…”
События в сказках складываются по тройственной схеме, с повторяющимися словесными фразами. Звучит утроенный мотив.
Например, обернувшись насекомым (мушкой, комаром, шмелём), Гвидон трижды посещает царство Салтана.
“В муху князь оборотился,
Полетел и опустился
Между моря и небес
На корабль – и в щель залез”.
На острове у него появляется три чуда: белка, царевна Лебедь и тридцать три богатыря. Балда побеждает бесёнка в трёх состязаниях: в беге, в бросании палки, в верховой езде и даёт попу три щелчка. Утроенный мотив, да и сама цифра три звучит и в сказке Ершова “Конёк-горбунок”.
“Стало в третий раз смеркаться,
Надо младшему сбираться…”
“Слушай: завтра на заре,
На широком на дворе
Должен челядь ты заставить
Три котла больших поставить…”
Широкое использование числа «3» у А.С. Пушкина в его знаменитой сказке «О попе и его работнике Балде»
С виду глупый работник Балда соглашается работать всего за 3 щелка. Жадный поп, считая себя умным и хитрым, надеется на «русское авось». Наступает уже срок расплаты, не на шутку испуганный поп хочет «погубить Балду, отправляет его к чертям собрать «недоимки за 3 года». Чтобы показать «русское лукавство» ума Балды, Пушкин использует традиционный утроенный мотив сказок – поединок с чёртом.
Три раза Балда в море «верёвку крутил», чертям покоя не давал. Мы ощущаем, как нетерпеливее, грознее становится Балда с каждым разом: в первый раз Балда «море морщил», во второй раз «наделал такого шуму, что все море смутилось и волнами так и расходилось», а в третий «Балда над морем опять шумит да чертям верёвкой грозит».
Три раза мерился силой Балда с «посланным бесёнком».
Первые два задания придумал чертёнок:
«кто скорее из нас обежит около моря».
«кто далее палку бросит».
А третье задание задал сам Балда:
«Кобылу подыми-ка ты,
Да неси её полверсты».
Мы видим, как хитрый Балда лихо и весело побеждает чёрта.
Не зря испугались черти Балды. С таким же страхом ждёт своей расплаты поп. С каждым щелком сила растёт. Мы чувствуем юмор в слове «щелк». Не удар, а щелк. Каким же должен быть удар Балды, если щелк его такой силы. Вот тебе и «глупый» Балда. Оказался он умнее и хитрее даже попа.
С первого щелчка
Прыгнул поп до потолка;
Со второго щелчка
Лишился он языка,
А с третьего щелчка
Вышибло ум у старика.
Поэт говорит о бесшабашности русского характера. Выражая свои симпатии Балде, автор презрительно смеется над бесёнком («ножки протянул») и над попом («со страху корчится»), которые вздумали тягаться «с самим Балдой».
Загадочная семерка
Семь чудес света. Семь дней недели. Семь цветов радуги. Семь недель поста. Семь смертных грехов. Француз дает самую сильную клятву: «Крепко, как семь». Счастливый чувствует себя на седьмом небе.
Названия сказок: «Волк и семеро козлят», «Семь козьих голов».
Пословицы: «Семь раз отмерь, один раз отрежь», «Семь бед – один ответ», «Семеро одного не ждут», «Семь пятниц на неделе».
Число «7» буквально пронизывает всю историю культуры народов Земли.
Зародился культ числа «7» в Древнем Вавилоне. Наблюдая небо, древние астрономы насчитывали 7 планет: Солнце, Луну, Меркурий, Венеру, Марс, Юпитер, Сатурн.
И все-таки, почему 7?
Может быть, почитание семерки связано не только с обожествлением планет? Ведь еще до вавилонян, уже у людей палеолита, было какое-то особое отношение к ритму «7» в орнаментации. Причем не только в Европе, но и в Азии.
Неожиданный ответ был найден американским ученым Миллером в психологии. Он объяснил особенности семерки пропускной способностью нервной системы человека. Статистика опыта подтвердила, что самые разные испытуемые могут без ошибок сравнить в среднем только 7 раздражителей. Человек при кратковременном восприятии может мгновенно охватить не более семи сходных элементов.
7 ЧУДЕС СВЕТА
Так называют прославленные в древности сооружения и статуи. Наверное, Филон Александрийский, живший в IV веке до н. э., и не подозревал, что его имя сохранится в веках по столь забавному поводу. Он, математик, механик, геодезист, составил первый вариант «Семи чудес света». Почему он выбрал именно 7 объектов, точно историки не знают. Самое распространенное объяснение: «семерка» считалась числом магическим, которое в своих наблюдениях за окружающим миром отметили еще древние египтяне. Это и семь цветов радуги, и семь небесных тел в Солнечной системе, видимых невооруженным глазом…
В свой труд «Семь чудес света» Филон Александрийский включил: Египетские пирамиды, Висячие сады Семирамиды, Храм Артемиды Эфесской, Статую Зевса Олимпийского, Галикарнасский мавзолей, Колосс Родосский, Александрийский маяк. (Приложение IV). До нас, к сожалению, дошло лишь одно из этих прекрасных творений человеческого разума и умелых человеческих рук – пирамиды – гробницы древних египетских царей – фараонов.
От Каира, столицы Египта, далеко на юг тянется цепь остроконечных искусственных гор белого желтоватого цветов. Это пирамиды. Самая большая их них – пирамида фараона Хеопса – высотой около 147 м, построена в начале 27 в. до н.э. Лишь на 2 м ниже пирамида Хефрена. Этому фараону показалась недостаточной гробница величиной с гору, и он приказал поставить рядом с ней каменного стража, вытесанного из целой скалы. У стража лицо человека и туловище льва. Называется он Сфинксом. Образ Сфинкса, мудрого, как человек, и сильного, как лев, внушал суеверный ужас, и люди называли его отцом трепета.
Другое «чудо света» - висячие сады Семирамиды – находилось в самом большом и богатом городе Древнего Востока – Вавилоне. Они были созданы по приказу царя Навуходоносора ІІ в 6 в. до н.э. для своей жены – царицы Семирамиды. Навуходоносор построил свой дворец на искусственно созданной площадке, поднятой на высоту шестиэтажного дома. К площадке уступами поднимались шесть рядов кирпичных арок – шесть аркад. На каждом уступе был насыпан слой земли и разведён цветущий сад. День и ночь сотни рабов вращали колоссальные колёса с кожаными вёдрами, подавая в висячие сады воду Евфрата.
Храм греческой богини Артемиды в городе Эфесе, в Малой Азии, считался третьим «чудом света». Храм представлял собой прямоугольное здание из камня и дерева, обнесённое со всех сторон двойной колоннадой из 127 колон. В 356 г. до н.э. некто Герострат, желая прославиться, пожёг храм. Его имя навеки стало символом бессмысленного варварства.
В северо-западной части Греции, в городе Олимпии, на родине Олимпийских игр, в 456г. до н.э. появился храм, посвящённый Зевсу – верховному богу древних греков. Храм украшала статуя бога, изваянная великим скульптором Фидием. Это четвёртое «чудо». Двенадцатиметровый Зевс восседал на троне из золота, слоновой кости, чёрного дерева и драгоценных камней. Голову его украшал золотой венок из оливковых ветвей – знак миролюбия грозного бога. Голова, плечи, руки, грудь были выточены из слоновой кости. Плащ, перекинутый через левое плечо, волосы и борода Зевса были изваяны из золота. Фидий наделил Зевса человеческим благородством. Его лицо, обрамлённое бородой и вьющимися волосами, было не только строгим, но и добрым. Казалось, что Зевс вот-вот улыбнётся, поднимется с трона и расправит могучие плечи.
В Малой Азии, в столице небольшого Карийского царства – Галикарнасе (ныне город Бодрум в Турции) находилось пятое «чудо» - великолепная гробница, построенная для царя Мавсола его вдовой – царицей Артемисией в середине 4 в. до н.э. Это было величественное сооружение из кирпича, облицованное изнутри и снаружи белым мрамо-
ром, высотой 60 м. Первый этаж, где покоилась урна с прахом, имел вид громадного куба. Второй этаж был обнесён снаружи мраморной колоннадой, а третий представлял собой многоступенчатую пирамиду. Её венчала четвёрка коней с колесницей, которой правили Мавсол и Артемисия (статуи Мавсола и Артемисии, а также другие украшения мавзолея хранятся сейчас в Британском музее в Лондоне). От имени Мавсола и произошло слово «мавзолей».
В 3 в. до н.э. на остров Родос напали войска правителя Передней Азии и Сирии Деметрия Полиоркета. Однако одолеть свободолюбивых родосцев Деметрию не удалось. В память об успешной обороне острова они решили поставить самую большую статую на свете. Это шестое «чудо», известное по именем Колосса Родосского.. Это было изображение бога солнца Гелиоса, которого жители острова считали своим покровителей.
На острове Фарос в устье реки Нила, рядом с городом Александрией, около 280 г. до н.э. был построен самый большой маяк древности. Высота этой трёхъярусной башни достигала 135 м. На её вершине в открытой каменной беседке пылал костёр, указывая путь кораблям.

7 В РУССКОМ ЯЗЫКЕ
Русские люди особенно любят семь. Они считают, что семь является союзом бога с человеком. В романе «Пиковая дама» семёрка всегда приносит Герману счастье. Даже теперь в России семь считается добрым. Говорят, что если человек живёт в седьмой комнате на седьмом этаже, то он будет счастлив.
Почему русские смотрят на семь с большой любовью? По-моему, это в основном имеет дело с христианством. Все знают, что христианская культура оказала огромное влияние на российскую нацию. Говорят, что небо состоит из семи ярусов, которые заключают в себе чистое серебро, чистое золото, жемчужину, платину, серебро, рубин, святой луч. В древности через наблюдение и измерение люди знали только семь планет – Солнце, Луна, Венера, Юпитер, Меркурий, Марс, Сатурн и люди связывали их с богом. Поэтому семь придали святые смыслы. В « Библии » Бог создавал мир шесть дней, и на седьмой день отдыхал. Иисус сказал семь слов на кресте. Число семь с древнейших времен играло важную роль, считалось волшебным, таинственным у самых разных народов мира.
Индийская философия древности учила, например, что Вселенная состоит из семи элементов. Древние египтяне полагали, что солнце и все небесные светила поднимаются по семи лестницам и проходят семь ворот. Знаменитый философ Древней Греции Аристотель утверждал, что небесная твердь состоит из семи кристальных сфер. Самая главная, высшая, седьмая сфера получила название "Седьмое небо". Кстати, именно отсюда идет современное шутливое выражение быть на седьмом небе (от счастья), то есть "находиться на верху блаженства".
Число семь вошло в легенду о сотворении мира в течение семи дней. Древние говорили о семи чудесах света. Рим был основан на семи холмах. К библейским источникам восходят общеизвестные выражения "книга за семью печатями" - о чем-то непонятном, неясном никому, "семь смертных грехов" и некоторые другие.
Рассказывая о мистическом числе семь (древнерусское седмь) в старинных народных поверьях и в схоластических церковных догматах, С. В. Максимов в книге "Крылатые слова" напоминает известный исторический факт: "Когда Галилей после открытия четырех спутников Юпитера по целым ночам любовался системой этой планеты, противники его не только не верили открытиям, но и утверждали, что они невозможны. Ученое невежество говорило: "Как в неделе семь дней, так и на небе семь планет (Солнце, Луна, Меркурий, Венера, Марс, Юпитер, Сатурн) и больше быть не может. Соединение малого мира человека с безграничным миром Вселенной происходит при помощи наших органов чувств, расположенных в семи отверстиях головы: два глаза, два уха, две ноздри и рот. Как нет более таких отверстий в голове, точно так не может быть и на небе более семи планет". Так утверждали семь кардиналов инквизиции, осудившие Галилея на заточение в 1633 году. По этому поводу писатель добавляет не без иронии: "Впоследствии оказалось, что у семи нянек дитя всегда без глазу, как и у этих семи совершенно слепых мудрецов мировая истина".
Если мы обратимся к сказкам и песням русского и других народов, то мы найдем в них и огнедышащего змея о семи головах (семиголовую гидру), и семимильные сапоги-скороходы, и сказочного храбреца, который "одним махом семерых побивахом", и такие выражения, как "у семи царей по семи дочерей", и шуточное "было у тещеньки семеро зятьев".
С числом семь мы встречаемся и теперь. Но уже не считаем его таким таинственным и мистическим, каким оно было в представлении наших далеких предков. Известные объективные явления природы лежат в основе того, что, скажем, спектр состоит из семи основных цветов, а в музыке выделяются семь тонов (нот) звукоряда. Математики давно обратили внимание на то, что 7 - это самое большое простое число в первом десятке. Это математическое объяснение проливает свет на древнее обожествление числа семь - самого большого из простых однозначных. Именно с величиной, размером связаны по смыслу многие старинные русские пословицы и поговорки, в которые входит число семью.
7 В ПОСЛОВИЦАХ И ПОГОВОРКАХ
1. Семеро не один, в обиду не дадим.
2. Семеро одного не ждут.
3. Семеро одну соломинку подымают.
4. Семь раз по - твоему, да хоть раз по моему.
5. Семь раз отмерь, один раз отрежь.
6. Семь лет не виделись, а сошлись и говорить нечего.
7. Старик – да лучше семерых молодых.
8. Семь бед – один ответ.
9. Семь деревень, а лошадка одна.
10. У пьяного – семь клетей, а проспится – один плетень.
11. В гору семеро тащат, а с горы и один столкнёт.
12. Невелик городок, да семь воевод.
13. У одной овечки да семь пастухов.
14. В семи дорогах один топор.
15. Из поповского рукава семеро штанов выходит.
16. На поминки идёт, пузо из семи овчин шьёт.
17. Попадья лукавая – змея семиглавая.
18. За семь вёрст да киселя хлебать.
19. Ковры семи шелков, а рубаха и не прядена.
20. Всем по семь, а мне по восемь.
21. От семи собак на распутье огрызается.
22. Беда! До беды семь лет: либо будет, либо нет.
Число p
Первое знакомство с числом p
В школьном курсе математики с числом p мы впервые встречаемся в 6 классе в теме: «Длина окружности и площадь круга». В учебнике мы сталкиваемся со следующим объяснением: «Длина окружности прямо пропорциональна длине её диаметра. Поэтому для всех окружностей отношение длины окружности к длине её диаметра является одним и тем же числом. Его обозначают греческой буквой p («читается «пи»»). Длина окружности: C=2pr; площадь круга S=pr2 ».
Потом, только в 9 классе мы опять встречаемся с числом p, но уже в курсе геометрии пытаются доказать длину окружности следующим образом. «Периметр любого правильного вписанного в окружность многоугольника является приближённым значением длины окружности. Чем больше число сторон такого многоугольника, тем точнее это приближённое значение, так как многоугольник при увеличении числа сторон всё ближе и ближе «прилегает» к окружности
Возникновение числа p
Более двух тысячелетий назад было подмечено, что все окружности длиннее своих диаметров в одно и то же число раз. Впоследствии это было доказано.
Отношение длины окружности к её диаметру лет 250 назад стали обозначать кратко одной буквой p. Эта греческая буква – первая буква греческого слова «периферия», что означает «окружность». В древнем Вавилоне считали, что окружность длиннее её диаметра в три раза (т.е. p приблизительно равно трём). Но древнегреческие геометры уже знали, что p не равно трём. Об этом мы знаем из школьного курса геометрии. Почему же тогда Бертран Рассел в своей книге «Кошмары выдающихся личностей» писал: «лицо p было скрыто маской. Все понимали, что сорвать её, оставшись при этом в живых, не сможет никто. Сквозь прорези маски пронзительно, безжалостно, холодно и загадочно смотрели глаза …».
Английский математик Август де Морган назвал как-то p «…загадочным числом 3,14159…, которое лезет в дверь, в окно и через крышу».
Число p связывают с окружностью. Однако это число появляется в различных математических результатах, в которых ни о какой окружности речи не идёт.
Записи числа p
2 знака после запятой:
p =3,14
510 знаков после запятой:
p =3,141 592 653 589 793 238 462 643 383 279 502 884 192 169 399 375 105 280 974 592 307 816 406 286 208 998 628 034 825 342 117 067 982 148 086 513 282 306 647 093 844 609 550 582 231 725 359 408 128 481 117 450 284 102 701 938 521 105 559 644 622 948 954 930 381 964 428 810 975 665 933 446 128 475 648 233….
Мнемоническое правило
-
Чтобы нам не ошибаться,
-
Надо правило прочесть:
-
Три, четырнадцать, пятнадцать,
-
Девяносто два и шесть.
-
Надо только постараться
-
И запомнить все как есть:
-
Три, четырнадцать, пятнадцать,
-
Девяносто два и шесть.
-
Три, четырнадцать, пятнадцать,
-
Девять, два, шесть, пять, три, пять.
-
Чтоб наукой заниматься
-
Это каждый должен знать.
Если подсчитать количество букв в каждом слове в нижеприведенных фразах (без учета знаков препинания) и записать эти цифры подряд, не забывая про десятичную запятую после первой цифры «3». Получится приближенное число p
Забавные факты
Международный день числа p 14 марта человечество отмечает Международный день числа p. Почему 14 марта? Если быть точнее, то поздравлять окружающих с днем «пи» нужно в марте 14-го в 1:59:26, в соответствии с цифрами числа p – 3,1415926…
Интересно, что праздник числа p, отмечающийся 14 марта, совпадает с днем рождения одного из наиболее выдающихся физиков современности Альбертом Эйнштейном.
Еще одной датой, связанной с числом p, является 22 июля, которою называют «Днем приближенного числа p», так как в европейском формате дат этот день записывается как 22/7. а значение этой дроби является приближенным значением числа p
Мировой рекорд по запоминанию знаков числа пи принадлежит японцу Акира Харагути. Он запомнил число p до 100- тысячного знака после запятой. Ему понадобилось почти 16 часов, чтобы назвать всё число целиком.
В штате Индиана (США) в 1897 был выпушен билль, законодательно устанавливающий значение числа p равным 3,2. Данный билль не стал законом благодаря своевременному вмешательству профессора Университета Пердью, присутствовавшем во время рассмотрения принятого данного закона.
Просмотр содержимого документа
«chislo_pi»
ЧИСЛО
![]()
Отношение длины окружности к её диаметру – величина постоянная и не зависит от размеров окружности. Число, выражающее это отношение , принято обозначать греческой буквой ( “ пи “ ) – первой буквой слова “ периферия “ ( греч. “ окружность “ ).
Общеупотребительным такое число стало с середины 18 века. Число выражается бесконечной непериодической десятичной дробью и приближённо равно 3,141592653589…
Математика Древнего Междуречья, Древнего Египта.
В глубокой древности считалось, что окружность ровно в 3 раза длиннее диаметра. Эти сведения содержатся в клинописных табличках Древнего Междуречья. Такое же значение можно извлечь из текста Библии: “ И сделал литое из меди море, - от края его и до края его десять локтей, - совсем круглое… и шнурок в тридцать локтей обнимал его кругом”. Однако уже во 2 тысячелетии до н.э. математики Древнего Египта находили более точное отношение. Важным достижением геометрической науки египтян было очень хорошее приближение числа , которое получается из формулы площади круга диаметра d:
S = ( d – 1/9d ) 2 = ( 1 – 1/9 ) 2 d2 .
Этому правилу из 50 – й задачи папируса Райнда (приблизительно 1650 г. до н.э.) соответствует значение = 4(8/9)2 = 3,1605. Однако каким образом египтяне получили саму формулу, из контекста неясно.
В Московском папирусе есть ещё одна интересная задача: вычисляется поверхность корзины “ с отверстием 4 ½ “. Исследователи толкуют её по – разному, поскольку в тексте не указано, какой формы была корзина. Но все сходятся во мнении, что и здесь для числа берётся то же самое приближённое значение 4 ( 8/9 )2. Замечательно, что на всём Древнем Востоке при вычислениях использовалось значение = 3.
В этом отношении египтяне намного опередили другие народы.
Математические достижения в Древней Греции.
С 6 века до н.э. математическая наука стремительно развивалась в Древней Греции. Древние греки Евдокс Книдский, Гиппократ и др. измерение окружности сводили к построению соответствующего отрезка, а измерение круга – к построению равновеликого квадрата.
Архимед в 3 веке до н.э. , занимаясь вычислениями длины окружности, установил, что “ периметр всякого круга равен утроенному диаметру с избытком, который меньше седьмой части диаметра, но больше десяти семьдесят первых “. В своей небольшой работе “ Измерение круга “ он обосновал три положения: 1) всякий круг равновелик прямоугольному треугольнику, катеты которого соответственно равны длине окружности и её радиусу; 2) площади круга относятся к квадрату, построенному на диаметре как 11 к 14; 3) отношение любой окружности к её диаметру меньше 3 1/7 и больше 3 10/71. (Вероятно, в первоисточнике третье предложение стояло на месте второго, но при переписке или переводе была допущена погрешность. Нужно заметить, что арабы располагали более точным текстом этой работы, чем мы.) Последнее предложение Архимед обосновал последовательным вычислением периметров правильных вписанных и описанных многоугольников при удвоении числа их сторон. Сначала он удвоил число сторон правильных описанного и вписанного шестиугольников, затем двенадцатиугольников и т.д., доведя до вычисления периметров правильного вписанного и описанного многоугольников с 96-ю сторонами.
Определение. Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
Определение. Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Определение. Если все стороны многоугольника касаются окружности, то многоугольник называется описанным около этой окружности.
Определение. Если все вершины многоугольника лежат на окружности, то многоугольник называется вписанным в эту окружность.)
По точным расчётам Архимеда отношение окружности к диаметру заключено между числами 3 10/71 и 3 1/7, а это означает, что =3,1419… Иначе говоря, Архимед указал границы числа
3,1408
Значение 3 1/7 до сих пор считается вполне хорошим приближением числа для прикладных задач. Более точное приближение 3 17/120 ( =3,14166) нашёл знаменитый астроном, создатель тригонометрии Клавдий Птолемей (2 в.), но оно не вошло в употребление.
Приближения числа “ ![]() “ в Индии и Китае.
“ в Индии и Китае.
В священной книге джайнизма ( одной из древнейших религий, существовавших в Индии и возникшей в 6 веке до н.э. ) имеется указание, из которого следует, что число “пи “ принимали равным дроби 3,162… Это значение приводит индийский математик 7 века Брахмагупта.
Китайские учёные в 3 веке использовали для значение 3 7/50, которое хуже приближения Архимеда. В конце 5 века китайский математик Цзу Чун Чжи получил приближение 355/113 ( =3,1415927). Оно осталось неизвестно европейцам и было вновь найдено нидерландским математиком Адрианом Антонисом лишь в 1585 г.
Число “ ![]() “ в Европе (15 – 16 вв.).
“ в Европе (15 – 16 вв.).
В первой половине 15 века в обсерватории Улугбека, возле Самарканда, астроном и математик ал-Каши вычислил “пи” с 16 десятичными знаками.
К концу 16 века в европейской математике сформировались понятия рациональных и иррациональных чисел. (Определение. Целые и дробные числа составляют множество рациональных чисел. Термин “ рациональное число “ произошёл от латинского слова ratio, что в переводе означает “ отношение “ (частное). Каждое рациональное число может быть представлено в виде бесконечной периодической дроби.
Определение. Бесконечные десятичные непериодические дроби представляют числа, не являющиеся рациональными. Их называют иррациональными числами (приставка “ир” означает отрицание).) Хотя многие были убеждены, что число - иррациональное, доказать это никто не мог.
В то же время некоторые математики продолжали заниматься вычислением числа . Спустя полтора столетия после ал-Каши в Европе Ф.Виет нашёл число “пи” только с 9 правильными десятичными знаками. Но при этом он первым сделал открытие, имеющее большое значение, так как позволило вычислять с какой угодно точностью.
Число Лудольфа.
Поиски точного выражения числа продолжались и после работ Ф.Виета. В начале 17 века голландский математик из Кёльна Лудольф ван Цейлен ( 1540 – 1610 ) – некоторые историки называют его Л.ван Кейлен – нашёл 32 знака. С тех пор ( год публикации 1615 )значение числа с 32 знаками получило название числа Лудольфа.
Идеальный математик.
Первым ввёл обозначение отношения длины окружности к диаметру современным символом английский математик У.Джонсон в 1706 г. В качестве символа он взял первую букву греческого слова “периферия”. Общеупотребительным введённое У.Джонсоном обозначение стало после работ Л.Эйлера, который воспользовался этим символом впервые в 1736 г.
ЭЙЛЕР ЛЕОНАРД (1707-1783)
Идеальный математик 18 века - так часто называют Эйлера. Это был недолгий век П росвещения, вклинившийся между эпохами жестокой нетерпимости. Всего за 6 лет до рождения Эйлера в Берлине была публично сожжена последняя ведьма. А через 6 лет после смерти Эйлера - в 1789 году - в Париже вспыхнула революция. Эйлеру повезло: он родился в маленькой тихой, куда изо всей Европы приезжали мастера и ученые, не желавшие тратить дорогое рабочее время на гражданские смуты или религиозные распри. Так переселилась в Базель из Голландии семья Бернулли: уникальное созвездие научных талантов во главе с братьями Якобом и Иоганном. По воле случая юный Эйлер попал в эту компанию и вскоре сделался достойным членом базельского "питомника гениев". Братья Бернулли увлеклись математикой, прочтя статьи Лейбница об исчислении производных и интегралов. Вскоре вокруг братьев сложился яркий математический кружок, и на полвека Базель стал третьим по важности научным центром Европы - после Парижа и Лондона, где уже процветали академии наук. Каждый год на кружке решались новые трудные и красивые задачи, а на смену им вставали новые увлекательные проблемы.
росвещения, вклинившийся между эпохами жестокой нетерпимости. Всего за 6 лет до рождения Эйлера в Берлине была публично сожжена последняя ведьма. А через 6 лет после смерти Эйлера - в 1789 году - в Париже вспыхнула революция. Эйлеру повезло: он родился в маленькой тихой, куда изо всей Европы приезжали мастера и ученые, не желавшие тратить дорогое рабочее время на гражданские смуты или религиозные распри. Так переселилась в Базель из Голландии семья Бернулли: уникальное созвездие научных талантов во главе с братьями Якобом и Иоганном. По воле случая юный Эйлер попал в эту компанию и вскоре сделался достойным членом базельского "питомника гениев". Братья Бернулли увлеклись математикой, прочтя статьи Лейбница об исчислении производных и интегралов. Вскоре вокруг братьев сложился яркий математический кружок, и на полвека Базель стал третьим по важности научным центром Европы - после Парижа и Лондона, где уже процветали академии наук. Каждый год на кружке решались новые трудные и красивые задачи, а на смену им вставали новые увлекательные проблемы.
Но когда ученые орлята подросли, выяснилось, что в Швейцарии не хватит места для их гнезд. Зато в далекой России, по замыслу Петра 1 и по проекту Лейбница, была учреждена в 1725 году Петербургская Академия Наук. Русских ученых не хватало, и тройка друзей: Леонард Эйлер с братьями Даниилом и Николаем Бернулли (сыновьями Иоганна) - отправилась туда, в поисках счастья и научных подвигов. Чем только не пришлось заниматься Эйлеру на новом месте! Он обрабатывал данные всероссийской переписи населения. Эту огромную работу Эйлер вел в одиночку, быстро проделывая все вычисления в уме: ведь компьютеров еще не было. Он расшифровывал дипломатические депеши, перехваченные русской контрразведкой. Оказалось, что эту работу математики выполняют быстрее и надежнее прочих специалистов. Он обучал молодых моряков высшей математике и астрономии, а также основам кораблестроения и управления парусным судном в штиль или в бурю. И еще составлял таблицы для артиллерийской стрельбы и таблицы движения Луны. Ведь в дальнем плавании Луна часто заменяла часы при определении долготы! Только гений мог, выполняя всю эту работу, не забыть о большой науке. Эйлер оказался гением. За 15 лет своего первого пребывания в России он успел написать первый в мире учебник теоретической механики (не учить же простого студента по сложным книгам Ньютона!), а также курс математической навигации и многие другие труды. Писал Эйлер легко и быстро, простым и понятным языком. Столь же быстро он выучивал новые языки, но вкуса к литературе не имел. Математика поглощала все его время и силы.
В 26 лет Эйлер был избран российским академиком, но через 8 лет он переехал из Петербурга в Берлин. В чем дело? Да, тогдашнее российское правительство было малограмотным и свирепым. Только что завершилось правление Анны Иоанновны, и возобновилась чехарда военных переворотов. Однако Эйлера это впрямую не касалось: считаться "немцем" в Петербурге было безопасно и престижно, а ученые немцы были на вес золота. Но Эйлер уже почувствовал себя одним из сильнейших математиков Европы - и вдруг заметил, что ему не с кем на равных поговорить о своей науке. Приезжая иностранная молодежь повзрослела и либо уехала из дикой и опасной России, либо погрязла в мелкой текущей работе. А первое поколение ученых россиян еще не выросло. Вспомним, что Ломоносова тогда послали на учебу в Германию! Эйлер решил переехать туда, где накал ученых дискуссий был повыше. Он выбрал Берлин, где молодой король Фридрих 2 Прусский решил создать научный центр не слабее парижского. Эйлер провел в Берлине четверть века, и считал эти годы лучшими в своей жизни. В Берлине Эйлер занимался всей математикой сразу, и почти все у него получалось. Например, захотелось ему перенести все методы математического анализа на функции, зависящие от комплексных чисел - и создал он теорию функций комплексного переменного. Попутно Эйлер выяснил, что показательная функция и синусоида суть две стороны одной медали. Аналогично было с Большой Теоремой Ферма. Услыхав о ней, Эйлер решил сам придумать утраченное доказательство - и вскоре обнаружил "метод спуска", найденный Ферма веком раньше. Проверив этот метод для степеней 3 и 4, Эйлер стал проверять его для следующего простого показателя - 5. Тут обнаружились неожиданные затруднения, и Эйлер оставил эту тему молодым исследователям. Но только в конце 20 века эта проблема, кажется, приблизилась к окончательному решению.
В геометрии Эйлер также оставил значительный след. Он искал в ней не столько новые изящные факты, сколько общие теоремы, не укладывающиеся в догматику Евклида. Например, теорема о связи между числами вершин, ребер и граней выпуклого многогранника. Эту формулу знал еще Декарт; но он не оставил ее доказательства. В Берлине "король математиков" Леонард Эйлер работал с 1741 по 1766 год; потом он покинул Берлин и вернулся в Россию. Надвигалась старость, выросла огромная семья, а новая российская царица Екатерина 2 (немка по происхождению) предложила Эйлеру гораздо лучшие условия жизни, чем предоставлял своим академикам скуповатый и капризный Фридрих 2. Тесное общение с научной молодежью Эйлера уже не увлекало; он торопился успеть изложить на бумаге те бесчисленные открытия и догадки, которые осенили его в золотую берлинскую пору. Все научные журналы Европы охотно печатали новые статьи Эйлера. Его трудоспособность и вдохновение с годами нарастали, и многие тексты увидели свет лишь после смерти автора. Переезд Эйлера в Петербург мало что изменил для математиков Европы. Великое светило лишь сместилось на восток, не исчезая с горизонта. Удивительно другое: слава Эйлера не закатилась и после того, как ученого поразила слепота (вскоре после переезда в Петербург). Неукротимый старец продолжал размышлять о математике и диктовать очередные статьи или книги до самой смерти. Она настигла его на 77 году жизни и на 16 году слепоты... В 1770-е годы вокруг Эйлера выросла Петербургская математическая школа, более чем наполовину состоявшая из русских ученых. Тогда же завершилась публикация главной его книги - "Основ дифференциального и интегрального исчисления", по которой учились все европейские математики с 1755 по 1830 год. Она выгодно отличается от "Начал" Евклида и от "Принципов" Ньютона. Возведя стройное здание математического анализа от самого фундамента, Эйлер не убрал те леса и лестницы, по которым он сам карабкался к своим открытиям. Многие красивые догадки и начальные идеи доказательств сохранены в тексте, несмотря на содержащиеся в них ошибки - в поучение всем наследникам эйлеровой мысли. Первый учебник, предназначенный не для последователей, а для исследователей: таково завещание Эйлера и всей эпохи Просвещения, адресованное грядущим векам и народам.
Иррациональность и трансцендентность числа “![]() ”.
”.
В 1766 г. немецкий математик Иоганн Ламберт строго доказал иррациональность числа : число “пи” не может быть представлено простыми дробями, как бы ни были велики числитель и знаменатель. И, тем не менее, история числа на этом не закончилась.
В конце 19 века профессор Мюнхенского университета Карл Фердинанд Линдеман нашёл строгое доказательство того, что - число не только иррациональное, но и трансцендентное, т.е. не может быть корнем никакого алгебраического уравнения. Его доказательство поставило точку в истории древнейшей математической задачи о квадратуре круга. ( Определение. Квадратура круга – неразрешимая задача построения при помощи циркуля и линейки квадрата, равного по площади данному кругу; вообще неразрешимая задача.) На протяжении тысячелетий она не поддавалась усилиям математиков, и выражение “квадратура круга “ даже стало синонимом неразрешимой проблемы. “Загадочное упорство” этой задачи, как оказалось, связано именно с природой числа .
В память об открытии трансцендентности числа в зале перед математической аудиторией Мюнхенского университета был установлен бюст Линдемана. На постаменте под его именем изображён круг, пересечённый квадратом равной площади, внутри которого начертана буква .
Число “![]() ” в современной математике.
” в современной математике.
К концу 19 века, после 20 лет упорного труда, англичанин Вильям Шенкс нашёл 707 знаков числа . Однако в 1945 г. обнаружено с помощью ЭВМ, что Шенкс в своих вычислениях допустил ошибку в 520-м знаке и дальнейшие его вычисления оказались неверными.
В наше время с помощью ЭВМ число вычислено с миллионами правильных знаков после запятой. Но такая точность не нужна ни в каких вычислениях и представляет скорее технический, чем научный интерес.
В современной математике число - это не только отношение длины окружности к диаметру, оно входит в большое число различных формул, в том числе и в формулы неевклидовой геометрии. Входит она и в замечательную формулу Л.Эйлера, которая устанавливает связь числа “пи” и числа “е”. Эта и другие взаимосвязи позволили математикам ещё глубже выяснить природу числа .
Как запомнить первые цифры числа “![]() ”.
”.
Три первые цифры числа = 3,14… запомнить совсем несложно. А для запоминания большего числа знаков существуют забавные поговорки и стихи. Например, такие:
Нужно только постараться
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
С.Бобров. ”Волшебный двурог”
Тот, кто выучит это четверостишие, всегда сможет назвать 8 знаков числа :
3,1415926…
В следующих фразах знаки числа можно определить по количеству букв в каждом слове:
“Что я знаю о кругах?” (3,1416 );
“Вот и знаю я число, именуемое Пи. – Молодец!”
( 3,1415927 );
“Учи и знай в числе известном за цифрой цифру, как удачу примечать”
( 3,14159265359 )
А так выглядит 101 знак числа “ ![]() ” без округления:
” без округления:
3, 14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230
78164 06286 20899 86280 34825 34211 70679.

Просмотр содержимого документа
«focusi»
МАТЕМАТИЧЕСКИЕ ФОКУСЫ

Фокусы развивают творческие начала личности, артистические способности, стимулируют потребность в творческом самовыражении. Математические фокусы способствуют концентрации внимания и активизации учащихся на уроках математики. Магия фокуса способна разбудить сонных, растормошить ленивых, заставить думать тугодумов. Ведь не разгадав секрета фокуса, невозможно понять и оценить всей его прелести. А секрет фокуса чаще всего имеет математическую природу.
Миллионы людей во всех частях света увлекаются математическими фокусами, которые являются очень своеобразной формой демонстрации математических закономерностей. И это не удивительно. “Гимнастика ума” полезна в любом возрасте, она тренируют память, обостряют сообразительность, вырабатывают настойчивость, способность логически мыслить, анализировать и сопоставлять.
Еще в Древней Элладе без игр не мыслилось гармоническое развитие личности. И игры древних не были только спортивными. Наши предки знали шахматы и шашки, не чужды им были ребусы и загадки. Таких игр во все времена не чуждались ученые, мыслители, педагоги. Они и создавали их. С древних времен известны головоломки Пифагора и Архимеда, русского флотоводца С.О. Макарова и американца С. Лойда.
На огромную познавательную и воспитательную ценность интеллектуальных игр неоднократно указывали К.Д. Ушинский, А.С. Макаренко, А.В. Луначарский. Среди тех, кто увлекался ими, были К.Э. Циолковский, К.С. Станиславский, И.Г. Эренбург и многие другие выдающиеся люди.
Отдельно хочется отметить американского математика, фокусника, журналиста, писателя и популяризатора науки Мартина Гарднера (Gardner).
Он родился 21 октября 1914 г. Окончил математический факультет Чикагского университета. Основатель (середина 50-х гг.), автор и ведущий (до 1983) рубрики "Математические игры" журнала «Scientific American» ("В мире науки"). От этого талантливого учёного и популяризатора науки читатели узнают о флексагонах, математических фокусах, поиске фальшивых монет, проблеме 3х+1, парадоксе узника и, конечно же, об изобретённой Джоном Конуэем игре "Жизнь", компьютерную модель которой хотя бы один раз создавали все, кто учился программированию. Гарднер трактует занимательность как синоним увлекательного, интересного в познании, но чуждого праздной развлекательности. Среди произведений Гарднера есть философские эссе, очерки по истории математики, математические фокусы и «комиксы», научно-популярные этюды, научно-фантастические рассказы, задачи на сообразительность.
Особую популярность снискали статьи и книги Гарднера по занимательной математике. В нашей стране было издано семь книг Мартина Гарднера, которые увлекают читателя и подталкивают к самостоятельным исследованиям «Гарднеровский» стиль характеризуют доходчивость, яркость и убедительность изложения, блеск и парадоксальность мысли, новизна и глубина научных идей.
Ниже приведены примеры 12 математических фокусов.
Фокус “Феноменальная память”.
Для проведения этого фокуса необходимо заготовить много карточек, на каждой из которых поставить ее номер (двузначное число) и записать семизначное число по особому алгоритму. “Фокусник” раздает карточки участникам и объявляет, что он запомнил числа, записанные на каждой карточке. Любой участник называет номер каточки, а фокусник, немного подумав, говорит, какое на этой карточке записано число. Разгадка данного фокуса проста: чтобы назвать число “фокусник” проделывает следующие действия – прибавляет к номеру карточки число 5, переворачивает цифры полученного двузначного числа, затем каждая следующая цифра получается сложением двух последних, если получается двузначное число, то берется цифра единиц. Например: номер карточки – 46. Прибавим 5, получим 51, переставим цифры – получим 15, будем складывать цифры, следующая – 6, затем 5+6=11, т. е. возьмем 1, потом 6+1=7, дальше цифры 8, 5. Число на карточке: 1561785.
Фокус “Угадать задуманное число”.
Фокусник предлагает кому-нибудь из учащихся написать на листе бумаги любое трехзначное число. Далее приписать к нему это же число еще раз. Получится шестизначное число. Передать лист соседу, пусть он разделит это число на 7. Передать листочек дальше, пусть следующий ученик разделит полученное число на 11. Снова передать результат дальше, следующий ученик пусть разделит полученное число на 13. Затем передать листочек “фокуснику”. Он может назвать задуманное число.
Разгадка фокуса:
Когда мы к трехзначному числу приписали такое же число, то мы тем самым умножили его на 1001, а затем, разделив последовательно на 7, 11, 13, мы разделили его на 1001, то есть получили задуманное трехзначное число.
Фокус “Волшебная таблица”.
На доске или экране таблица, в которой известным образом в пяти столбцах записаны числа от 1 до 31. Фокусник предлагает присутствующим задумать любое число из этой таблицы и указать, в каких столбиках таблицы находится это число. После этого он называет задуманное вами число.
Разгадка фокуса:
Например вы задумали число 27. Это число находится в 1-ом, 2-ом, 4-ом и 5-ом столбиках. Достаточно сложить числа, расположенные в последней строке таблицы в соответствующих столбиках, и получим задуманное число. (1+2+8+16=27).
Фокус “Угадать зачеркнутую цифру”.
Пусть кто-либо задумает какое-нибудь многозначное число, например, число 847. Предложите ему найти сумму цифр этого числа (8+4+7=19) и отнять ее от задуманного числа. Получится: 847-19=828. в том числе, которое получится, пусть он зачеркнет цифру – безразлично какую, и сообщит вам все остальные. Вы немедленно назовете ему зачеркнутую цифру, хотя не знаете задуманного числа и не видели, что с ним проделывалось.
Выполняется это очень просто: подыскивается такая цифра, которая вместе с суммою вам сообщенных цифр составила бы ближайшее число, делящееся на 9 без остатка. Если, например, в числе 828 была зачеркнута первая цифра (8) и вам сообщили цифры 2 и 8, то, сложив 2+8, вы соображаете, что до ближайшего числа, делящегося на 9, т. е. до 18 – не хватает 8. Это и есть зачеркнутая цифра.
Почему так получается?
Потому что если от какого-либо числа отнять сумму его цифр, то останется число, делящееся на 9 без остатка, иначе говоря такое, сумма цифр которого делится на 9. В самом деле, пусть в задуманном числе а – цифра сотен, в – цифра десятков, с – цифра единиц. Значит всего в этом числе единиц 100а+10в+с. Отнимая от этого числа сумму цифр (а+в+с), получим: 100а+10в+с-(а+в+с)=99а+9в=9(11а+в), т. е. число, делящееся на 9. При выполнении фокуса может случиться, что сумма сообщенных вам цифр сама делится на 9, например 4 и 5.Это показывает, что зачеркнутая цифра либо 0, либо 9.Тогда вы должны ответить: 0 или 9.
Фокус “У кого какая карточка?”.
Для проведения фокуса необходим ассистент. На столе лежат три карточки с оценками: “3”, “4”, “5”. Три человека подходят к столу и каждый берет одну из карточек и показывает ее ассистенту “фокусника”. “Фокусник”, не глядя, должен угадать кто что взял. Ассистент говорит ему: “Угадывай” и “фокусник” называет у кого какая карточка.
Разгадка фокуса:
Рассмотрим возможные варианты. Карточки могут располагаться следующим образом: 3, 4, 5 4, 3, 5 5, 3, 4
3, 5, 4 4, 5, 3 5, 4, 3
Так как ассистент видит, какую карточку взял каждый человек, то он будет помогать “фокуснику”. Для этого нужно запомнить 6 сигналов. Пронумеруем шесть случаев:
Первый – 3, 4, 5
Второй – 3, 5, 4
Третий – 4, 3, 5
Четвертый – 4, 5, 3
Пятый – 5, 3, 4
Шестой – 5, 4, 3
Если случай первый, то ассистент говорит: “Готово!”
Если случай второй – то: “Так, готово!”
Если случай третий – то: “Угадывай!”
Если четвертый – то: “Так, угадывай!”
Если пятый – то: “Отгадывай!”
Если шестой – то: “Так, отгадывай!”.
Таким образом, если вариант начинается с цифры 3, то “Готово!”, если с цифры 4, то “Угадывай!”, если с цифры 5, то “Отгадывай!”, а карточки учащиеся берут по очереди.
Фокус “Любимая цифра”.
Любой из присутствующих задумывает свою любимую цифру. Фокусник предлагает ему выполнить умножение числа 15873 на любимую цифру, умноженную на 7. Например, если любимая цифра 5, то пусть умножит на 35. Получится произведение, записанное только любимой цифрой. Возможен и второй вариант: умножить число 12345679 на любимую цифру, умноженную на 9, в нашем случае это число 45. Объяснение этого фокуса достаточно простое: если умножить 15873 на 7, то получится 111111, а если умножить 12345679 на 9, то получится 111111111.
Фокус “Угадать задуманное число, ничего не спрашивая”.
Фокусник предлагает учащимся следующие действия:
Первый ученик задумывает какое-нибудь двузначное число, второй – приписывает к нему справа и слева такое же число, третий – делит полученное шестизначное число на 7, четвертый – на 3, пятый – на 13, шестой – на 37 и передает свой ответ задумавшему, который видит, что к нему вернулось его число. Секрет фокуса: если к любому двузначному числу приписать справа и слева такое же число, то двузначное число при этом увеличится в 10101 раз. Число 10101 равно произведению чисел 3, 7, 13 и 37, поэтому после деления мы и получаем задуманное число.
Конкурс болельщиков – “Веселый счет”. От каждой команды приглашается представитель. На доске две таблицы, на которых в беспорядке отмечены числа от 1 до 25. По сигналу ведущего учащиеся должны найти на таблице все числа по порядку, кто это сделает быстрее, тот и выиграл.
Фокус “Число в конверте”
Фокусник пишет на бумажке число 1089, вкладывает бумажку в конверт и заклеивает его. Предлагает кому-нибудь, дав ему этот конверт, написать на нем трехзначное число такое, чтобы крайние цифры в нем были различны и отличались бы друг от друга больше, чем на 1. Пусть затем он поменяет местами крайние цифры и вычтет из большего трехзначного числа меньшее. В результате пусть он снова переставит крайние цифры и получившееся трехзначное число прибавит к разности двух первых. Когда он получит сумму, фокусник предлагает ему вскрыть конверт. Там он найдет бумажку с числом 1089, которое у него и получилось.
Фокус “Угадывание дня, месяца и года рождения”
Фокусник предлагает учащимся выполнить следующие действия: “Умножьте номер месяца, в котором вы родились, на 100, затем прибавьте день рождения, результат умножьте на 2, к полученному числу прибавьте 2, результат умножьте на 5, к полученному числу прибавьте 1, к результату припишите 0, к полученному числу прибавьте еще 1 и, наконец, прибавьте число ваших лет. После этого сообщите, какое число у вас получилось”. Теперь “фокуснику” осталось от названного числа отнять 111, а потом остаток разбить на три грани справа налево по две цифры. Средние две цифры обозначают день рождения, первые две или одна – номер месяца, а последние две цифры – число лет, зная число лет, фокусник определяет год рождения.
Фокус “Угадать задуманный день недели”.
Пронумеруем все дни недели: понедельник – первый, вторник – второй и т. д. Пусть кто-нибудь задумает любой день недели. Фокусник предлагает ему следующие действия: умножить номер задуманного дня на 2, к произведению прибавить 5, полученную сумму умножить на 5, к полученному числу приписать в конце 0, результат сообщить фокуснику. Из этого числа он вычитает 250 и число сотен будет номером задуманного дня. Разгадка фокуса: допустим, задуман четверг, то есть 4 день. Выполним действия: ((4×2+5)*5)*10=650, 650 – 250=400.
Фокус “Угадать возраст”.
Фокусник предлагает кому-нибудь из учащихся умножить число своих лет на 10, затем любое однозначное число умножить на 9, из первого произведения вычесть второе и сообщить полученную разность. В этом числе “фокусник” должен цифру единиц сложить с цифрой десятков – получится число лет.

Просмотр содержимого документа
«iz_istorii»
ИЗ ИСТОРИИ МАТЕМАТИЧЕСКИХ ТЕРМИНОВ

-
«ЛИНИЯ» происходит от латинского слова «линеа» - льняная (имеется в виду льняная нить).
От этого же корня происходит наше слово линолеум, первоначально означавшее льняное полотно.

-
КВАДРАТ произошел от латинского слова «кваттуор» (четыре) - фигура с четырьмя сторонами.
-
РОМБ происходит от латинского слова «ромбус», означающего бубен.
Мы привыкли к тому, что бубен имеет круглую форму , но раньше бубны имели форму квадрата или ромба , о чем свидетельствуют изображения «бубен» на игральных картах.

-
ТРАПЕЦИЯ происходит от латинского слова «трапезиум» -столик.
От этого же слова происходит наше слово « трапеза», означающее стол.

-
Слово ДИАГОНАЛЬ происходит от греческого « диа», что означает «через» и « гония» - угол, т.е. рассекающая углы, проходящая через углы.
-
КОНУС – это латинская форма греческого слова «конос», что означает сосновую шишку.

-
ЦИЛИНДР происходит от латинского слова «цилиндрус», означающего «валик», «каток».

-
ПРИЗМА – латинская форма греческого слова «присма» - опиленная (имелось в виду опиленное бревно).

-
Пирамида – латинская форма греческого слова «пюрамис», которым греки называли египетские пирамиды; это слово происходит от древнеегипетского слова «пурама», которым эти пирамиды называли сами египтяне.
Рассмотрим истоки слова и термина «пирамида». Сразу стоит отметить что «пирамида» или “pyramid” (английский), “piramide” (французский, испанский и славянские языки), “pyramide” (немецкий) - это западный термин, берущий свой исток в древней Греции. В древнегреческом πύραμίς («пирамис» и мн. ч. πύραμίδες «пирамидес») имеет несколько значений. Древние греки именовали «пирамис» пшеничный пирог, который напоминал форму египетских сооружений. Позже это слово стало означать «монументальную структуру с квадратной площадью в основании и с наклонными сторонам, встречающимися на вершине». Происхождение греческого слова πύραμίς имеет собственную историю. По одной из версий греки заимствовали это слово из Египта, где есть схожее по звучанию “Pir E Mit” , означающее «часть числа» или «составляющая часть совершенства», но не пирамиду, как сооружение. Этимологический словарь указывает, что греческое «пирамис» происходит из египетского “pimar”.
Из греческого слово перешло в латинский язык и вплоть до 16 века не трансформировалось в европейских языках, поскольку в средневековой Европе о пирамидах в Египте знали лишь образованные люди, говорящие на латыни. Первое письменное толкование слова «пирамида» встречается в Европе в 1555 г. и означает: «один из видов древних сооружений королей». После открытия пирамид в Мексике и с развитием наук в 18 веке, пирамида стала не просто древним памятников архитектуры, но и правильной геометрической фигурой с четырьмя симметричными сторонами (1716 г.).

-
СФЕРА – латинская форма греческого слова «сфайр» - мяч.

-
Точка – (лат. “пункт” – пунктир; “пунктум” – укол, медицинский термин “пункция” – прокол).
-
Термин «параллелограмм» греческого происхождения и, согласно Проклу, был введен Евклидом. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцам.
-
Корень – (квадратный или корень уравнения) пришло от арабов. Арабские ученые представляли себе квадрат числа, вырастающий из корня – как растение, и потому называли корнями.
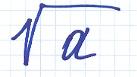
-
Алгоритм. В IX в. ал-Хорезми изложил позиционную систему в сочинении "Об индийском числе". Латинский перевод этого труда начинался словами: "Dixit Algorithmi", - сказал ал-Хорезми". Отсюда и произошел термин "алгоритм" ("алгорифм"). В средневековой Европе слово означало всю систему десятичной позиционной арифметики.
Современное понятие алгоритма установилось в середине 30-х годов XX в. в работах Геделя, Чёрча, Тьюринга, Поста, А.А. Маркова. Алгоритм - точное формальное предписание, однозначно определяющее содержание и последовательность операций, переводящих заданную совокупность исходных данных в искомый результат.
В начальной школе простейшими алгоритмами являются правила, по которым выполняются сложение, вычитание, умножение, деление.
-
Алгебра. Математическая наука, объектом изучения которой являются алгебраические системы, например группы, кольца, поля и др. Отдельной ветвью алгебры является элементарная алгебра.
Первый учебник алгебры - "Краткая книга об исчислении ал-Джабра и ал-Мукабалы" был написан в 825 г. арабским ученым ал-Хорезми. Слово ал-джабр при этом означало операцию переноса вычитаемых из одной части в другую и его буквальный смысл - "восполнение". Этот термин стал названием науки. В Европе такое название употреблялось уже в самом начале XIII в., но еще Ньютон называл алгебру "Общей арифметикой" (1707). Книга ал-Хорезми имеет особое значение в истории математики как руководство, по которому долгое время обучалась вся Европа. Именно под влиянием арабской математики алгебра сформировалась как учение о решении уравнений.
-
Слово «хорда» происходит от греческого слова «хорде» — «кишка», «струна» (в древней Греции струны выделывались из воловьих кишок). И в Древней Греции, и в александрийской школе это слово не связывалось с хордой. И Евклид, и Птолемей, и другие александрийские ученые называли хорду «прямой в круге», имея в виду прямолинейный отрезок, вписанный в круг (треугольник, вписанный в круг, они также называли «треугольником в круге»).
Аксиома. Термин впервые встречается у Аристотеля и перешел в математику от философов древней Греции. В переводе с греческого слово означает "достоинство", "уважение", "авторитет". Первоначально термин имел смысл "самоочевидная истина".
-
В современном понимании аксиома - высказывание некоторой теории, принимаемое при построении этой теории без доказательства, т.е. принимаемое как исходное, отправное для доказательств других положений этой теории (теорем). Аксиомы называют также постулатами.

-
Геометрия (греч. geometria, от ge — Земля и metreo — мерю), раздел математики, изучающий пространственные отношения и формы, а также другие отношений и формы, сходные с пространственными по своей структуре.
Происхождение термина «Геометрия", что буквально означает «землемерие», можно объяснить следующими словами, приписываемыми древнегреческому учёному Евдему Родосскому (4 в. до н. э.): «Геометрия была открыта египтянами и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития р. Нил, постоянно смывавшего границы». Уже у древних греков Геометрия означала математическую науку, в то время как для науки об измерении Земли был введён термин геодезия. Судя по сохранившимся отрывкам древнеегипетских сочинений, Геометрия развилась не только из измерений Земли, но также из измерений объёмов и поверхностей при земляных и строительных работах и т.п. Первоначальные понятия Геометрия возникли в результате отвлечения от всяких свойств и отношений тел, кроме взаимного расположения и величины. Первые выражаются в прикосновении или прилегании тел друг к другу, в том, что одно тело есть часть другого, в расположении «между», «внутри» и т.п. Вторые выражаются в понятиях «больше», «меньше», в понятии о равенстве тел.
-
Слово «синус» — латинского происхождения. Если мы посмотрим в латинско-русский словарь, мы увидим там такие значения этого слова: 1) изогнутость, кривизна, изгиб, выпуклость; 2) пазуха, карман, складка тоги (древнеримская одежда) на груди; 3) платье, одежда; 4) грудь, объятия; 5) нежная любовь, забота; 6) середина, центр; 7) убежище, прибежище; 8) залив, бухта; 9) впадина, углубление, провал. Слово «синус» хорошо известно врачам в значении «пазуха», «впадина». Однако ни одно из этих многочисленных значений не имеет никакого отношения к синусу в тригонометрии. Откуда же произошел этот термин?
Тригонометрия появилась впервые в I—II веках нашей эры в Александрии, в работах знаменитых александрийских астрономов, наиболее крупным из которых был Клавдий Птолемей. Однако в тригонометрии Птолемея основным понятием был не синус, а хорда. В книге Птолемея «Математическая система» были таблицы зависимости длин хорд от длин стягиваемых ими дуг, причем дуги измерялись в градусах, минутах и секундах, а хорды— в частях радиуса: здесь радиус считался равным 60 частям, хорды измерялись в этих долях радиуса, в их «минутах» (60-х долях) и в их «секундах» (60-х долях «минут»). Это «шестидесятеричное» деление дуг и хорд было заимствовано александрийскими астрономами у вавилонян.

Просмотр содержимого документа
«kalendar»
КАЛЕНДАРЬ

Слово календарь произошло от латинских слов "caleo" – провозглашать и "calendarium" – долговая книга. Первое напоминает о том, что в древнем Риме начало каждого месяца провозглашалось особо, второе – что первого числа месяца там было принято уплачивать проценты по долгам. Календарем принято называть систему счисления продолжительных промежутков времени, использующую периодичность явлений природы, проявляющуюся особенно отчетливо в движениях небесных светил.
-
Первичные формы счисления времени.
По богатому этнографическому материалу можно проследить, как одинаковые формы хозяйственного уклада приводят к образованию сходных календарных понятий. У всех народностей имеется понятие года; год подразделяется на сезоны, число которых чаще всего равно четырем, но может доходить до семи. Сезоны распадаются на менее крупные интервалы (от 10 до 12 в году), имеющие связь с лунными месяцами. Названия месяцев отражают хозяйственную основу быта, так, например, у сибирских эвенков-оленеводов имеется месяц «когда олень обдирает кожу с рогов», месяц «отела»; у тунгусов с берегов Амура есть месяц «прихода кеты», месяц «икрометания». Наблюдения светил имеют несомненную связь со счетом времени; у нанайцев имеется месяц «когда голова Медведя перед рассветом заходит». В тропических странах двойной цикл полевых работ (2 посева и 2 жатвы) совпадает с определенным положением на небе созвездия Ориона, в других странах столь же важную роль играют Плеяды.
-
Календарь майя.
В основу календаря майя была положена мифическая начальная дата – 13 августа 3113 года до нашей эры. От нее – то путем простого отсчета количества прошедших дней и велось летосчисление.
Календарная система майя включала 269-дневный счет по 13 дням недели (связан с периодом беременности - "цолькин"), 365-дневный счет, сориентированный по Солнцу (состоял из 17-20-дневных месяцев и пяти добавочных дней - "хааб"), и 52-летний большой цикл, разработанный на основе комбинации двух первых календарей.
Большую роль в жизни майя играли 20-летний малый (короткий счет - "катун") и лунный циклы.
Для обозначения чисел и месяцев майя использовали точки и линейки.

Математике и календарю подчинялась даже архитектура. Майя строили свои сооружения не в силу необходимости, а тогда, когда им приказывал это календарь: каждые 5, 10 и 20 лет. И обязательно с указанием даты постройки. Это было связано с убеждением в существовании тесной взаимосвязи Земли и Космоса, основанной на принципах гармонического резонанса.

Календарь майя, несмотря на свою древность, удивительно точен. По современным расчетам, продолжительность солнечного года составляет 365,2422 дня. Майя вычислили значение в 365,2420 дня. Разница – всего в две десятитысячные. Для составления столь точного календаря, по мнению ученых, потребовалось бы наблюдать и записывать движения планет на протяжении приблизительно десяти тысяч лет.
-
Древний китайский календарь.
Над составлением и усовершенствованием календаря китайские астрономы трудились много веков. Примерно за тысячу лет до нашей эры ими была уточнена продолжительность лунного месяца и солнечного года: соответственно 29,5 суток и 365,25 суток. На этой основе и были созданы лунно-солнечные календари.
Месяцы по такому календарю начинались с новолуния. Началом нового года считалось новолуние, предшествовавшее вступлению Солнца в созвездие Водолея. Этот момент приходился на январь-февраль; к этому времени среднесуточная температура воздуха значительно повышалась, и наступал период подготовки к весенним полевым работам. Месяцы не имели собственных названий, а только порядковые номера: первый, второй, третий и так далее.
В период династии Цинь (246-201 до н.э.) был разработан и начал применяться сезонный сельскохозяйственный календарь, в котором календарный год был разделен на 24 сезона в зависимости от положения Солнца на эклиптике. Деление года на сезоны существовало независимо от деления на месяцы, связанное с движением Луны.
При помощи такого сезонного календаря крестьянам было легче определять сроки посева, сбора урожая и выполнять другие сельскохозяйственные работы. Вот фрагмент календаря «Ся-сяо-чжень», использовавшегося в эпоху Ся:
«I месяц. В начале ночи созвездие Цан (Орион) бывает в середине неба, хвост Большой Медведицы обращен книзу. В начале года земледельцы приготавливают сохи и выходят для размежевания полей; приносят жертву изобретателю сохи... После морозов греет Солнце и все оттаивает. Выходят из нор полевые крысы... Опушаются ивы. Куры садятся на яйца и выводят цыплят. В это время бывает большой ветер...
III месяц. В начале ночи созвездие Цан скрывается на западе. Молятся об урожае пшеницы, так как в этом месяце бывают небольшие засухи. Цветут тополя... подрастают ягнята. Полевые крысы превращаются в перепелок...
IX месяц. Высевают озимую пшеницу. Воробьи, скрываясь в море, превращаются в устриц».
Деление календарного года по климатическим периодам является одной из особенностей китайского календаря. В деревнях часто применяют сезонный календарь и в настоящее время. С ним связано много пословиц и поговорок, сложившихся на основе многолетних наблюдений за явлениями природы.
Календарь использовался и для астрологических целей. В нем отразилась вера людей в предсказания. Древние китайцы верили, что по расположению небесных светил можно определить свою судьбу, выбрать удачный день для начала тех или иных дел, избежать опасности. Так, например, второй день I месяца считался несчастливым, в этот день нельзя было начинать никаких важных дел. Третий день I месяца считался удачным для начала торговых дел. А в четвертый день рекомендовалось брить голову, приниматься за лечение и тому подобное.
Вера в астрологию заставляла постоянно совершенствовать календарь, изобретать все новые и новые способы счета времени.
Китайский календарь не имеет аналогов среди европейских календарей. Это так называемый 60-летний циклический календарь.
С глубокой древности в Китае ведут счет времени по «Таблицам циклических знаков». Точная дата введения циклических знаков неизвестна. Легенда относит зарождение циклических таблиц для счета времени к эпохе полулегендарной династии Хуан Ди. Достоверно известно, что этот способ уже применялся во времена периода Чуньцю («Весна и Осень», 722-481 до н.э.). Началом китайского летосчисления принято считать 2387 г. до н.э. «Таблицы циклических знаков» применялись в Китае вплоть до революции 1911 г. В Пекинском университете хранятся кости животных и панцири черепах с вырезанными на них циклическими знаками 60-летнего цикла.
Китайский календарь — это календарь лунно–солнечно–юпитерианский. С древнейших времен в странах Восточной и Юго-Восточной Азии при составлении календарей большое значение придавали периодичности движения не только Солнца и Луны, но и Юпитера и Сатурна. Хотя астрономическая наука тогда еще не располагала точными данными о времени обращения планет (считалось, что все планеты вращаются вокруг Земли), все же было определено, что Юпитер совершает свой кругооборот примерно за 12, а Сатурн — за 30 лет. Кроме того, придавая большое значение символике чисел, и особенно поискам циклов в движении космических тел, китайские составители календаря подобрали такое соотношение периодов обращения планет Юпитера и Сатурна, при котором исключались бы дробные результаты деления большего числа на меньшее. Так, они приняли за основу цикла время двух оборотов Сатурна, равное 60 годам. За это время Юпитер совершает пять оборотов.
Каждый год внутри круга получает свое иероглифическое обозначение. Построение цикла показано в таблице 1, состоящей из 5 двойных столбцов, соответствующих 5 «стихиям», или «элементам» (дерево, огонь, земля, металл, вода – их знаки: Му, Хо, Ту, Цзинь, Шуй). Каждая стихия может быть представлена в двух состояниях: мужском (нечетные столбцы) или женском (четные столбцы). Так получаются 10 шестичленных периодов, или «небесных ветвей»; каждая из них имеет свой циклический знак. Каждая из 12 строк составляет один пятичленный период, или одну «земную ветвь» со своим циклическим знаком; каждая из ветвей обозначается еще названием животного (мышь, корова, тигр и т.д.).
В нечетные «земные ветви» входят только номера годов из мужских столбцов; в четные – только годы из женских столбцов. Каждый год получает двойное название (первое – знак столбца, второе – знак строки). Так, год первый имеет циклические знаки Цзя-Цзы, его название – год «дерева и мыши», год 7-ой имеет знаки Гэн-У и называется годом «металла и коня» и т.д. Переход от года данного цикла к следующему году соответствует переходу в таблице направо вниз по диагонали. Если известен 1-й год данного цикла в европейском счислении, то обозначение любого другого года внутри цикла легко определить по таблице. Так, 1-м годом текущего теперь китайского цикла был 1924 н.э. Поэтому 1955 год, который является 32-м годом того же цикла, есть год «дерева и овцы». 60-летняя система счета годов получила название «бытовой».
После китайской революции 1911 года с 1 января 1912 года в Китае стали применять наряду с 60-летним циклическим календарем и григорианский календарь. В настоящее время много периодических изданий выходит с двойной датой: по григорианскому календарю и по 60-летнему циклическому.
-
Древнеегипетский календарь
Древнеегипетский календарь, связанный с видимым годичным движением Солнца, является прообразом всех так называемых солнечных календарей. Он был создан еще в 4-м тысячелетии до н. э. с целью регулирования полевых работ.

Известно, что около 2800 до н. э. основной единицей счёта времени был год; он делился на 3 сезона (наводнение, зима и посев, жатва) по 4 месяца в каждом. Месяц подразделялся на 3 декады, то есть имел 30 дней. После 12 месяцев в календарь вставлялись ещё 5 дополнительных дней. Таким образом, все годы имели одинаковую длину в 365 дней. Начало календарного года фиксировалось днём первого видимого (или гелиакического, то есть происходящего на фоне зари) восхода Сириуса ( Большого Пса). В древнейшие периоды египетской истории первый восход Сириуса на широте Мемфиса приходился приблизительно на 19 июля, если считать по так называемому юлианскому календарю. Но в те эпохи эта дата почти совпадала с днём летнего солнцестояния (ныне оно передвинулось на 22 июня). В дни солнцестояния происходит разлив Нила — событие первостепенной важности для земледельческого Египта. Однако средний промежуток между двумя гелиакическими восходами Сириуса равен не 365 дням, а почти точно 365,25 дня. Поэтому, продвигаясь постепенно вперёд по всем датам календарного года, восход Сириуса обходил весь круг египетских календарных дат в 3654=1460 египетских лет; но так как только 1461 египетский год по 365 дней равен 1460 годам Сириуса по 365,25 дня, то цикл заканчивался лишь после истечения этого промежутка времени («периода Сотиса»). Таким образом, календарный египетский год в 365 дней был «блуждающим» по отношению к солнцестоянию и к первому восходу Сириуса.
-
Армянский календарь и календарь Омар Хайяма. Александрийское счисление.
Система египетского блуждающего года получила некоторое распространение в Средней Азии; там она действовала с 7 века н. э. параллельно с системой мусульманского лунного календаря. Подобная же система действовала в Армении; после 12 месяцев по 30 дней вставлялось 5 дополнительных дней. Начальная эра этого счисления, то есть 1-е навасарди 1-го года армянской эры, приходилась на 10 июля 552 н. э., но с каждым 4-летием начало армянского года отступало на 1 день назад в счёте по юлианскому календарю. Совпадение начальных дней обоих счислений произошло только в 14 веке (1-е навасарди 766 армянской эры есть 1-е января 1317 н. э.). Несколько позднее армянский календарь (так называемый «томар») был заменён юлианским.
Знаменитый таджикский поэт и учёный Омар Хайям (ум. в 1123) создал один из самых совершенных солнечных календарей. В нём на 33 года приходится 8 високосных лет, таким образом, средняя длина года в этом цикле равна 365,24242 дня, что больше истинной длины тропического года всего на 19 сек. Начальная эпоха этого счисления («эра Джалала, или эра Малики») — 15 марта 1079 года.
В Египте во: время правления римского императора Августа (27 до н.э.— 14 н.э.) был тоже совершён переход от блуждающего года к более совершенным формам счисления. В ту эпоху начало египетского года (1-е тот) приходилось на 29 августа (считая по юлианскому календарю). С целью навсегда удержать 1-е тот в том же положении относительно солнцестояния и первого восхода Сириуса, 4-летие с 26 по 22 год до н. э. было удлинено на один дополнительный день, затем такие же вставки (интеркаляции) делались 1 раз в 4 года. Так возникло Александрийское счисление; средняя длина года в нём равна 365¼ дня. От юлианского календаря оно отличается только тем, что 6-й дополнительный день вводится на 3-м году 4-летнего цикла; поэтому 1-е тот соответствует всегда либо 30 августа (в годах, предшествующих юлианским високосам), либо 29 августа во всех остальных. Начальная эра этого счисления 29 августа 284 н. э. («эра Диоклетиана»).
-
Мусульманский лунный календарь.
Мусульманский лунный календарь, так называемый хиджра, является единственным, в котором течение календарных месяцев связывается только с изменением фаз Луны. К чисто лунному календарю предъявляется только одно условие: начало календарных месяцев должно по возможности соответствовать моментам новолуний; поэтому единственный эталон длительности в этой системе есть средняя длина лунного синодического месяца, или месяца лунных фаз, равная 29 дням 12 часам 44 минутам 2,9 секундам = 29,530588 дня. В лунном календаре естественно считать месяцы попеременно в 29 и в 30 дней. 12 таких лунных месяцев дают лунный год в 354 дня; он на 11 дней (в среднем) короче тропического года, поэтому начала лунных годов отступают в нашем счислении с каждым лунным годом на 11 дней и обходят весь круг времён года приблизительно в 33 года. Хотя лунный календарь мало пригоден для планирования хозяйственной жизни, им по традиции пользуются народы Турции и Пакистана. До Великой Октябрьской социалистической революции он применялся и у некоторых народностей СССР. Так как продолжительность 12 лунных месяцев равна 354,3071 дня (а не 354 дням), то и в календарь вводились удлинённые (так называемые лунно-високосные) годы в 355 дней. Распределение их в календаре будет наилучшим тогда, когда цикл из определённого числа лунно-високосных и лунно-простых лет (по 354 дня) будет в возможной точности равен целому числу дней; таких циклов два: «турецкий», где на протяжении 8 календарных лунных лет вставляется 3 високосных, и «арабский», в котором на 30 календарных лунных лет приходится 11 високосных. Ошибка первого составляет +0,06 дня, второго — всего –0,01 дня; эта последняя достигает 1 дня только через 100 циклов, то есть через 3 тысячи лет, следовательно, этот цикл весьма точен. В лунно-високосных годах на 1 день удлиняется последний месяц. Началом счисления в годах хиджры принимается первый день первого месяца того года, в котором, по преданию, произошло бегство, или переселение, Мухаммеда (Магомета) из Мекки в Медину: по юлианскому календарю 16 июля 622 н. э. (пятница).
-
Лунно-солнечное счисление. Основные циклы.
Задачи, стоящие перед так называемым лунно-солнечным календарем, значительно сложнее, так как он должен быть согласован и со сменой лунных фаз и с наступлением начал астрономического года, то есть с равноденствиями. Для определения соответствующих циклов исходим из основных данных:
1 солнечный год — 365,2422 суток
1 лунный месяц – 29,5306 суток.
Отсюда получаем отношение:
![]()
Дробная часть этого отношения, будучи развёрнута в непрерывную дробь, даёт следующие подходящие дроби:
![]()
Предпоследняя из них приводит к следующему приближённому равенству:
1 солнечный год = ![]() лунного месяца, или 19 солнечных лет=235 лунным месяцам, что служит основой лунно-солнечного календаря. Календарные лунные месяцы имеют либо 29, либо 30 дней (в первом случае они называются «пустыми», во втором — «полными»). Считая солнечный год, как у александрийцев, равным З65¼ дня, найдём: 19 солнечных лет = 69393/4 дня = 235 лунным месяцам. Взяв 110 пустых и 125 полных, получим как раз 6940 дней. Итак, 19 солнечных лет приближённо равны 110 месяцам пустым + 125 полным. Этот результат составляет так называемое «золотое правило» хронологии, высказанное впервые древнегреческим астрономом Метоном (в 433 до н.э.). Оно служит основой почти всех действовавших лунно-солнечных систем. Для приспособления его к календарю следует только распределить все месяцы по 19 годам круга. Обычно считают 12 лет по 12 лунных месяцев и 7 лет по 13 лунных месяцев. Вставные тринадцатые месяцы получили название «эмболисмических» (от греч. έμβολισμός — вставка, включение). Порядковое число года в 19-летнем круге называется золотым числом этого года.
лунного месяца, или 19 солнечных лет=235 лунным месяцам, что служит основой лунно-солнечного календаря. Календарные лунные месяцы имеют либо 29, либо 30 дней (в первом случае они называются «пустыми», во втором — «полными»). Считая солнечный год, как у александрийцев, равным З65¼ дня, найдём: 19 солнечных лет = 69393/4 дня = 235 лунным месяцам. Взяв 110 пустых и 125 полных, получим как раз 6940 дней. Итак, 19 солнечных лет приближённо равны 110 месяцам пустым + 125 полным. Этот результат составляет так называемое «золотое правило» хронологии, высказанное впервые древнегреческим астрономом Метоном (в 433 до н.э.). Оно служит основой почти всех действовавших лунно-солнечных систем. Для приспособления его к календарю следует только распределить все месяцы по 19 годам круга. Обычно считают 12 лет по 12 лунных месяцев и 7 лет по 13 лунных месяцев. Вставные тринадцатые месяцы получили название «эмболисмических» (от греч. έμβολισμός — вставка, включение). Порядковое число года в 19-летнем круге называется золотым числом этого года.
-
Древневавилонский и древнееврейский календари.
Древневавилонский календарь был выработан уже в начале 3-го тысячелетия до н.э. Год состоял из 12 месяцев; начало их определялось непосредственным наблюдением первого появления лунного серпа. Когда с течением времени первый лунный месяц года слишком далеко отходил от весеннего равноденствия, год удлинялся вставкой 13-го месяца. Происхождение этих вставок, несомненно, связано со сменой времён года — основой периодичности хозяйственной деятельности людей. В 6 веке до н. э. в Вавилоне применялся неточный 8-летний круг, а с 380 до н. э.— исключительно 19-летний круг.
Та же система лунно-солнечного календаря лежала и в основе древнееврейского летосчисления; но окончательная выработка довольно сложных правил этого календаря произошла только в 5 веке н. э. На 19 лет круга полагается 7 лет по 13 лунных месяцев. Поэтому календарные годы могут быть или обыкновенные (длина их 353, 354 или 355 дней), или же эмболисмические (их продолжительность — 383, 384 или 385 дней). Вставной месяц повторяет 6-й месяц года (адар) и носит название второго адара (веадар). Начальным месяцем в древности был весенний месяц нисан; 15-го числа этого месяца празднуется еврейская пасха. В последние столетия перед нашей эрой начало еврейского года было перенесено на осень (новолуние осеннего месяца тишри). Начальная дата еврейского летосчисления есть условный момент 7 октября 3761 до н. э., это так называемая эра иудеев.
-
Древнегреческий календарь.
В Древней Греции действовали исключительно упомянутые выше циклы. Установление «октаэтериды», то есть 8-летнего круга, относится к 6 веку до н. э. В этом круге считали 48 пустых месяцев и 51 полный, что даёт 2 922 дня с довольно значительной ошибкой в 1,5 дня против действительной продолжительности 99 лунных месяцев (2923,53 дня). Год начинался обычно с летнего солнцестояния; поэтому в календаре, согласованном с Солнцем, начала лунных календарных месяцев должны были через несколько циклов заметно отходить от дней новолуния. В основу древнегреческой хронологии историк Тимей (р. ок. 345—340 — ум. ок. 250 до н. э.) положил счёт времени по олимпиадам — всенародным празднествам и играм, происходившим 1 раз в 4 года в Олимпии. Эрой олимпиад принимается лето 776 до н. э.; по преданию, в этом году происходила первая олимпиада. Годы в этом счислении обозначаются номером олимпиады и номером года в 4-летии, что записывается, например, так: олимпиада 117,3, причём олимпиада 1,1 соответствует 776 до н. э. Для перевода этих датировок в обычный исторический счёт в годах до нашей эры нужно номер олимпиады, уменьшенный на 1, умножить на 4, прибавить номер года в данной олимпиаде, тоже уменьшенный на 1, и вычесть сумму из 776; так, например, олимпиада 117,3 соответствует 776 — (1104 + 2) = 310 до н. э.
-
Древнеримский календарь и его реформа при Юлии Цезаре.
Первичной формой счисления времени у древних римлян служил аграрный год, непосредственно связанный с циклом полевых работ. В ранние периоды римской истории этот аграрный год начинался с марта; он состоял из 10 месяцев, носивших привычные для нас названия, кроме 5-го и 6-го месяцев (лат. quintilis от quintus — пятый и sextilis от sextus — шестой). Около 700 до н. э. число месяцев было увеличено двумя, вставленными перед мартом (январь и февраль). Кроме того, тогда же была введена в Риме и примитивная форма лунно-солнечного летосчисления. Возникла необходимость определять дни новолуний либо непосредственным наблюдением первого появления серпа молодой Луны, либо предвычислениями. Эти обязанности постепенно перешли к касте жрецов (понтификов); в классовых интересах верхушки рабовладельческого общества они могли вносить произвол и путаницу в счёт времени. Календы издревле являлись днём денежных расчётов; передвигая дни календ, можно было нарушать все сроки обязательств, внесения налогов и т. п. Устранение произвола и путаницы в действующем календаре стало острой экономической проблемой, требующей разрешения. В 46 до н. э. Юлий Цезарь произвёл коренную ломку римского календаря. По совету египетского учёного Созигена он перешёл к простым формам египетского солнечного года. В календаре Цезаря продолжительность четырёхлетия была определена в 1461 день; она получилась из сочетаний 3 лет по 365 дней и 1 года в 366 дней; начало года было перенесено на 1 января, с которого начинался римский хозяйственный год, но продолжительность отдельных месяцев была существенно изменена.

Весьма своеобразен у римлян был счёт дней внутри каждого месяца. Они не обозначали их порядковыми числами: 1-е, 2-е и т. д., а отсчитывали всегда назад от 3 определённых моментов внутри каждого месяца; то были упомянутые уже календы (Calendae) — первый день месяца, долженствовавший совпадать с новолунием, затем ноны (Nonae) — день первой четверти Луны, наконец, иды (Idus) — полнолуние. Римляне говорили, например: «в шестой день перед мартовскими календами», или «в третий день перец январскими нонами» н т. п.
В новом календаре остался только 1 вставной день. Цезарь поместил его тоже в феврале, в наших обозначениях между 23 и 24 февраля; у римлян этот день назывался ante diem bissextum Calendas Martias, то есть повторный шестой день перед мартовскими календами; из сочетания слов bis sextus возникло впоследствии одно слово: bissextus, откуда произошло русское «високос». Роль этого дня теперь играет 29 февраля, вставляемое в календарь один раз в четырёхлетие. Правильное применение юлианского календаря началось с 7 года н. э., с этой эпохи и вплоть до григорианской реформы все годы юлианского календаря, порядковое число которых делится на 4, являются високосными. Тогда же месяцы «квинтилис» и «сек-стилис» были переименованы в июль и август (в честь Юлия Цезаря и Октавиана, получившего титул Августа, то есть «священного»).
-
Календарь в допетровской России.
Древнеславянские названия месяцев, которые перешли в ряд славянских языков и отчасти удержались, например, в украинском и белорусском, свидетельствуют о большом внимании к явлениям природы. Таковы, например, Травень, Листопад, Грудень, Студень и т. д. Однако уже в летописях эти названия уступают место привычным нам латинским (и созвучным с ними новогреческим).
С 14—15 вв. в церковно-славянском изложении календарных вопросов создаётся несколько новых хронологических элементов. Важнейший из них есть так называемый «вруцелето», то есть день недели на 1 сентября текущего года. Эти дни, из которых первый есть «неделя», то есть воскресенье, обозначались буквами славянского алфавита (неделя – аз, понедельник – веди, и далее: глаголь, добро, есть, зело, земля). Зная «вруцелето» для данного года, можно без труда определить день недели (в современном смысле) на любую дату этого года. Эра русских летописцев «от сотворения мира» (отнесенного к 21 марта 5509 года до н.э.) применялась в двух «стилях»: первично началом года считалось 1 марта, а с конца 15 века (по-видимому, с 1492) начало года было перенесено на 1 сентября. Сентябрьское начало года и счисление лет «от сотворения мира» удержались на Руси до 1700 года. Петр I указом от 15 декабря 1699 года установил новое начало года: вслед за 31 декабря 7208 «от сотворения мира» наступило 1 января 1700 года н.э.
-
Григорианская реформа календаря.
В юлианском календаре и в александрийском счислении средняя длина года принята равной 365 дням 6 часам; она больше действительной длины тропического года на 11 минут 14 секунд. Поэтому за каждые 128 лет астрономическое равноденствие происходит на 1 день раньше, чем это следует по календарю. В 325 году на Никейском церковном соборе впервые был составлен так называемый христианский календарь. Весеннее равноденствие в этот год приходилось на 21 марта. Постановлением Никейского собора день равноденствия был «навсегда» связан с 21 марта по юлианскому календарю. Поэтому непрерывное отступление равноденствия от этой даты являлось изъяном календаря, требовавшим устранения. Неточность календаря стала предметом богословских споров. Вопрос об исправлении календаря дебатировался на пятом лютеранском соборе (1512—17), куда Николай Коперник был приглашён представить своё мнение о календарной реформе. Коперник считал, что длина года еще недостаточно точно известна, чтобы исправлять календарь. Реформа была проведена лишь в конце 16 века при папе Григории XIII (в 1582). Было предписано следующую после четверга 4 октября 1582 пятницу считать 15 октября. Весеннее равноденствие 1583 года с 11 марта было возвращено на 21 марта, в чём и состояла первая задача григорианской реформы; таким образом, осуществился переход на новый стиль. Помимо этого, реформа предусмотрела и исправление юлианского календаря. Так как юлианский календарь опаздывал почти на 3 дня в 400-летие, было решено впредь каждые 400 календарных юлианских лет укорачивать на 3 дня. Для этого годы, порядковое число которых делится на 100, стали считать високосными только в том случае, когда число сотен в них делится на 4. Исходная 10-дневная разница обоих календарей (старого и нового стилей) в последующем нарастает: в 18 веке — 11 дней, в 19 веке — 12 дней, в 20 и 21 веках — 13 дней, в 22 веке — 14 дней и т. д.
Средняя величина года в григорианском календаре превосходит истинную длину тропического года на 26 секунд; эта ошибка составит 1 сутки лишь за 3300 лет. Григорианский календарь был немедленно введён в действие во Франции, Италии, Испании и Португалии; в других странах — значительно позднее. В дореволюционной России вопрос о переходе на новый общераспространённый стиль несколько раз безуспешно выдвигался прогрессивными кругами общества, и лишь после Великой Октябрьской социалистической революции вопрос о реформе календаря получил своё разрешение. Декретом Совета Народных Комиссаров РСФСР от 26 января 1918 новый календарь был введён с 1 февраля (по старому стилю) 1918: вместо 1 февраля старого стиля считалось 14 февраля нового стиля.
-
Календарь французской революции 1798 года.
На следующий же день после свержения королевской власти во Франции (21 сентября 1792 года) было объявлено, что отныне «все общественные акты будут датироваться 1 годом Свободы». Через несколько месяцев был подготовлен детальный проект нового календаря, узаконенный Конвентом 5 декабря 1793 года. Основные элементы нового летосчисления были следующие: христианская эра и григорианский календарь отменяются; начало года с 1 января переносится на день осеннего равноденствия; первый год французской эры начинается 22 сентября 1792 года (которое совпало с днём равноденствия). Никакой системы вставки високосных годов по 366 дней не устанавливается, начало года определяется каждый раз астрономическими вычислениями. Впрочем, високосные годы в дальнейшем шли либо 1 раз в 4 года, либо 1 раз в 5 лет, когда они назывались «задержанными». Год состоял из 12 месяцев по 30 дней в каждом, месяцы делились на 3 декады. После 360 дней вводились 5 или 6 «дополнительных» дней (первично названных «санкюлотидами»). Праздничными днями считались: 1-й день 1-го месяца, 10-й, 20-й, 30-й день каждого месяца и все дополнительные дни. Названия дней недели имели в основе латинские количественные числительные: primidi – первый день, duodi – второй день, tridi – третий день, quartidi - четвёртый день (от лат. Primus — первый, duo — два, tres — три, quartidi — четвёртый и dies — день) и т. д. Названия месяцев приведены в табл. 2.
Таблица 2.
| Месяцы календаря французской революции 1789 года. | ||
| Осенние | вандемьер | месяц сбора винограда |
| брюмер | месяц туманов | |
| фример | месяц заморозков | |
| Зимние | нивоз | месяц снегов |
| плювиоз | месяц дождей | |
| вентоз | месяц ветров | |
| Весенние | жерминаль | месяц произрастания |
| флореаль | месяц цветения | |
| прериаль | месяц лугов | |
| Летние | мессидор | месяц колосьев |
| термидор | месяц жары | |
| фрюктидор | месяц плодов | |
Республиканский календарь был отменён в 1806 году, в период наполеоновской империи, и был вновь восстановлен во время Парижской Коммуны: март и апрель 1871 года считались месяцами жерминалем и флореалем 79 французской эры. После этого вновь был введён григорианский календарь.
Просмотр содержимого документа
«koleso»
ИЗОБРЕТЕНИЕ КОЛЕСА

О дним из самых важных, но простых изобретений, сделанных человеком,- это обыкновенное колесо. Интересно, что первые древние колеса были найдены там, где человек уже освоил плавку металла в Месопотамии, Средней Азии, Венгрии. Любопытно, что изобрели колесо вовсе не для того, чтобы быстрее передвигаться. Пока древние люди вели кочевой образ жизни, они весь свой нехитрый скарб носили с собой. А вот когда они осели на одном месте, тогда им понадобилось колесо. Оседлый человек стал засевать поля, разводить скот, строить большие поселения, а потом и города, началась торговля камнем, лесом, зерном. При этом людям приходилось перемещать огромные тяжести на большие расстояния. И идея колеса не могла не родиться.
дним из самых важных, но простых изобретений, сделанных человеком,- это обыкновенное колесо. Интересно, что первые древние колеса были найдены там, где человек уже освоил плавку металла в Месопотамии, Средней Азии, Венгрии. Любопытно, что изобрели колесо вовсе не для того, чтобы быстрее передвигаться. Пока древние люди вели кочевой образ жизни, они весь свой нехитрый скарб носили с собой. А вот когда они осели на одном месте, тогда им понадобилось колесо. Оседлый человек стал засевать поля, разводить скот, строить большие поселения, а потом и города, началась торговля камнем, лесом, зерном. При этом людям приходилось перемещать огромные тяжести на большие расстояния. И идея колеса не могла не родиться.
Постоянно имея дело с поваленными деревьями и бревнами, человек обнаружил, что они могут кататься. Оказывается, что само бревно, которое он с товарищами едва мог перенести на несколько метров, могло катиться само, если, конечно, его толкнуть.
Но чтобы, это сделать, нужно было приложить огромное усилие. Тогда кроманьонцы изобрели рычаг: подложили толстую длинную палку под бревно, нажали, и бревно покатилось. Потом догадались на катящиеся бревна наискосок положить другое бревно - они покатили и его. Значит, транспортируемые бревна уже сами могли быть «транспортом».
И все же этот метод оказался очень неудобным. Ближайшие к рычагам бревна все время падали. Нужно было их как-то зафиксировать. Неизвестно, что натолкнуло человека на эту идею, но когда он реализовал ее, то получилась первая повозка, грубая, неказистая. Однако она могла катиться лишь по ровной поверхности. Любой камень, оказавшийся на пути, мог разрушить ее. Тогда, прочно скрепили десяток бревен между собой, внизу прикрепили еще по две пары гладко отесанных бревен, а между ними поместили третье - гладкое. И получился первый каток, он прекрасно двигался. Это был прообраз колеса.
все же этот метод оказался очень неудобным. Ближайшие к рычагам бревна все время падали. Нужно было их как-то зафиксировать. Неизвестно, что натолкнуло человека на эту идею, но когда он реализовал ее, то получилась первая повозка, грубая, неказистая. Однако она могла катиться лишь по ровной поверхности. Любой камень, оказавшийся на пути, мог разрушить ее. Тогда, прочно скрепили десяток бревен между собой, внизу прикрепили еще по две пары гладко отесанных бревен, а между ними поместили третье - гладкое. И получился первый каток, он прекрасно двигался. Это был прообраз колеса.
Изображения салазок с колесиками (3000 г. до н. э.) найдены в Междуречье в шумерском городе Урук. К 2700 году до н. э. там же появляются рисунки повозок. В это же время шумеры начинают хоронить своих царей вместе с колесницами. Эти погребения найдены в Кише, Уре, в эламском городе Сузы.

Наскальный рисунок повозки II тыс. до н.э., обнаруженный в Ливии
По Востоку распространяется образ колеса как символа солнца и власти. Хетты клянутся колесом, в индийском эпосе бог Индра похищает колесо у бога солнца Сурьи, у иранцев Небесное Колесо - оружие богов. Ассоциация понятна: солнце - круглое и могущественное, колесо - тоже круглое и дарит человеку скорость, а с ней преимущество в бою и власть. Нам, привыкшим к быстрой езде, не понять, как скорость в 25-30 км/ч пьянила пешее дотоле человечество. Хотя лошадь приручили на тысячу лет позже, и повозку еще долго таскали онагры - азиатские ослы.
Но как деревянное колесо могло появиться в Месопотамии, отнюдь не изобиловавшей лесами? Подходящие леса были на востоке Турции и севере Ирана. Эти области и считали родиной колеса, пока археологи не обнаружили в армяно-грузинском пограничье и верховьях Куры многочисленные и даже более древние, чем в Междуречье, колесничные захоронения рубежа ГУ-Ш тыс. до н. э. Когда из-за строительства Севанской ГЭС уровень воды в озере упал, обнажились погребения с колесницами - тяжелыми и неповоротливыми. Тянуть их могли только волы.
Быстро катясь по свету, колесо почти одновременно с Месопотамией попадает на север. Древние захоронения с повозкой найдены у Элисты в Калмыкии. А дальше, в степи, ему уже нет границ: следующее древнейшее колесо нашли в селе Герасимовка Оренбургской области.
Уже в середине III тысячелетия до н. э. деревянное колесо оборачивали в кожу, а к 2000 г. до н. э. стали забивать в обод медные гвозди острием наружу - для лучшего сцепления с землей. Колеса еще сплошные, но уже не вырезанные из цельного ствола, а составные, сколоченные из трех частей. Такую древесину найти легче. Примерно тогда же люди приручают лошадь, и повозки разделяются на быстрые конные двуколки - боевые колесницы и экипажи правителя - и двухосные телеги с впряженным волом - для хозяйства.

Колесо III тыс. до н. э., найденное при раскопках месопотамского города-государ ства Ур
Повозка едет на восток через степи Азии от одних племен к другим (слово «телега» - монгольского происхождения). Это фиксируют наскальные рисунки южной Сибири. Кочевники-скотоводы делают большие крытые повозки - дома на колесах. К середине II тысячелетия до н. э. колесо докатилось до Китая эпохи царства Инь.
Слова «коло» и «рото» - колесо - были в индоевропейском, общем предке германских, славянских, романских, иранских языков... Значит, они возникли на прародине индоариев - в восточной Турции и северном Ираке в III тысячелетии до н. э. Именно оттуда начинается расселение племен, включая великую миграцию индоариев в Европу. Ученые до сих пор спорят, каким маршрутом они продвигались: из Малой Азии на Балканы, через Причерноморские степи в Венгрию, через Среднюю Азию - или всеми этими путями одновременно? В любом случае, их победоносное шествие было в немалой степени обеспечено военным успехом колесниц. По ходу миграции совершенствуется и само колесо. У того, что к 2000 году до н. э. доехало до нынешней Голландии, уже имелись спицы и обод.
Дальнейшее развитие колеса в Европе связано почти исключительно с кельтскими племенами. Около 1500 года до н. э. они научились «обувать» обод металлом, а через пару веков, ко времени Троянской войны, колесница становится почти целиком металлической. На таких сражаются гомеровские герои. Такими восхищается библейский пророк Наум: «По улицам несутся колесницы, гремят на площадях; блеск от них, как от огня; сверкают, как молния». Усовершенствование повозки продолжается. Две оглобли вместо одной видны на рельефе ассирийского царя Ашшурнасирпала II (850 г. до н. э.). А на другом краю земли, в датском Дьерберге наскальный рисунок (1век до н. э.) изображает повозку с подвижной передней осью: до нее телеги были крайне неповоротливы. В Риме они такими и остались. Кстати, воевавшие с варварами-кельтами римляне строили лучшие в мире дороги, но почти не занимались транспортными средствами, за исключением того, что научились около 100 года до н. э. запрягать коней цугом. Однако в быту по-прежнему использовались тяжелые колеса без спиц, и Вергилий называет телеги «скрипучими» и «стонущими», хотя ступицы смазывали жиром или дегтем. Эти повозки разбивали дорогу, и в 50 году до н. э. был принят первый закон, ограничивший нагрузку на одно колесо до 250 кг. Зато у римлян колесо заработало в водяной мельнице и в лебедке.

Колесо Дхармы на барельефе из буддийского святилища Санчи в Индии - символ ступеней духовного совершенствования (11-1 вв. до н. э.)
За три тысячи лет своего вращения колесо перевернуло жизнь почти всего Старого Света. А вот до Африки южнее Сахары, до Юго-Восточной Азии и, по понятным причинам, до Австралии так и не докатилось. Приплыв в Америку, испанцы были поражены тем, что инки не знали колеса. В Новом Свете не было крупного скота, за исключением лам, и инки надрывались на волоке. А ацтеки использовали колеса лишь в игрушках.
Есть и иная гипотеза изобретения колеса. Горшки - неказистые и кособокие - люди лепили еще за 6000 лет до н. э. Но появился гончарный круг - и вид посуды резко улучшился. А гончарный круг - это колесо, положенное набок. Кто у кого заимствовал идею, возница у гончара или наоборот? А вдруг окажется, что всеми переселениями народов, прогрессом транспорта и вообще всеми изменениями в облике планеты мы обязаны безымянному гончару, упрямо добивавшемуся, чтобы его горшки были ровными?

Просмотр содержимого документа
«labirint»
Из истории появления лабиринтов
Чтобы уяснить, что же такое ЛАБИРИНТ, лучше сначала обратить взоры к его предтечам и истокам, которые лежат в далеком прошлом.
Вообще, само слово "лабиринт" имеет несколько значений. Правильнее было бы сказать даже – существует несколько различных сущностей, называющихся этим словом. Обратимся к словарям:
Лабиринт - от немецкого Labyrinth (лат.labyrinthos, греч.labyrinthos)
1.чего. Запутанная сеть ходов, переходов, улиц, сообщающихся друг с другом помещений, откуда трудно выбраться.
2.перен. чего. Запутанные отношения, положения, из которых трудно найти выход. Лабиринт мыслей. В лабиринте противоречий.
3.В регулярных парках XVII – XVIII вв.: участок с затейливым расположением узких дорожек между высокими стенками стриженых кустов.
В словаре Ожегова: ЛАБИРИНТ - запутанные дорожки, переходы, место, откуда трудно найти исход, произошло от древних зданий в Египте и на Крите.
Прежде всего, это сам образ лабиринта. Лабиринт - это не просто совокупность запутанных коридоров, это странное, вечно меняющееся место, причудливое переплетение иных времён и измерений. Лабиринт принимает всё и всех, все найдут в нём себе место, но нити Ариадны в нём не существует: выйти из него невозможно, т.к. Лабиринт, по сути, не имеет границ. Лабиринт - нечто иррациональное, таинственное, мистическое.
Очень многие считают, что название «лабиринт» произошло от слова «лаброс» - такая обоюдоострая секира, часто изображаемая на фресках Кносского дворца. Это трудно доказать и трудно оспорить. Но самое забавное в том, что именно кносский дворец и считают лабиринтом, ссылаясь на то, что там много комнат, запутанные переходы, коридоры, лестницы… Ну, если бы это было так, то Минотавр, который по легендам, жил именно в лабиринте, должен был бы бродить беспрепятственно в покоях дворца в поисках своих жертв. А это нонсенс.
Древние легенды рассказывают, что Лабиринт спроектировал и построил знаменитый ученый, скульптор, зодчий и механик того времени – Дедал, которого все помнят как создателя крыльев. Упоминается, что Дедал строил Кносский Лабиринт по образцу египетского, описанного Геродотом. Египетский лабиринт насчитывал 3000 подземных и наземных комнат, однако считается, что Дедал воспроизвёл лишь одну сотую его часть.
Дедал, талантом своим в строительном славен искусстве,
Зданье воздвиг; перепутал значки и глаза в заблужденье
Ввел кривизною его, закоулками всяких проходов.
Овидий
 Найденные при раскопках критские монеты подтверждают то, что Лабиринт был самостоятельным сооружением, (подобные по конфигурации, правда каменные лабиринты, найдены во многих частях света, начиная от Англии, Норвегии, Соловецкого архипелага и заканчивая Южной Америкой). Более того, на критских монетах изображен так называемый «правильный или классический» лабиринт, в котором отсутствуют тупики, карманы, ложные хода, и в котором невозможно сбиться с пути.
Найденные при раскопках критские монеты подтверждают то, что Лабиринт был самостоятельным сооружением, (подобные по конфигурации, правда каменные лабиринты, найдены во многих частях света, начиная от Англии, Норвегии, Соловецкого архипелага и заканчивая Южной Америкой). Более того, на критских монетах изображен так называемый «правильный или классический» лабиринт, в котором отсутствуют тупики, карманы, ложные хода, и в котором невозможно сбиться с пути.
Многие древние легенды и сказания народов мира говорят о лабиринтах как о «входах» в подземное (потустороннее) царство, открывающихся тем, кто знал соответствующие заклятия, или оказывался поблизости в тот момент, когда этот вход открывался. Вот в подземном лабиринте и было самое место для Минотавра.
А вот описание Геродота: "Я видел этот лабиринт: он выше всякого описания. Ведь если бы собрать все стены и великие сооружения, воздвигнутые эллинами, то в общем оказалось бы, что на них затрачено меньше труда и денежных средств, чем на один этот лабиринт. Конечно, пирамиды - это огромные сооружения, и каждая из них по величине стоит многих творений (эллинского строительного искусства), вместе взятых, хотя и они также велики. Однако лабиринт превосходит (размерами) и эти пирамиды. В нем двенадцать дворов с вратами, расположенными одни против других, причем шесть обращены на север, а шесть на юг, прилегая друг к другу. Снаружи вокруг них проходит одна-единственная стена. Внутри этой стены расположены покои двух родов: одни подземные, другие над землею, числом 3000, именно по 1500 тех или других. По наземным покоям мне самому пришлось проходить и осматривать их, и я говорю о них как очевидец. О подземных же покоях знаю лишь по рассказам: смотрители ни за что не желали показать их, говоря, что там находятся гробницы царей, воздвигших этот лабиринт, а также гробницы священных крокодилов. Поэтому-то я говорю о нижних покоях лишь понаслышке. Верхние же покои, которые мне пришлось видеть, превосходят (все) творения рук человеческих. Переходы через покои и извилистые проходы через дворы, будучи весьма запутанными, вызывают чувство бесконечного изумления: из дворов переходишь в покои, из покоев в галереи с колоннадами, затем снова в покои и оттуда опять во дворы." (Геродот. История)
Если спросить у любого нашего современника, что такое лабиринт, то ответ наверняка будет такой: лабиринт — это сложная путаница ходов. Однако в пралабиринте — прадедушке всех лабиринтов — нет ничего подобного. Заблудиться в нем невозможно, поскольку нет ни перекрестков, ни развилок. Начиная со входа, путь неизбежно ведет к центру. Уместно возникает вопрос: а лабиринт ли это вообще? Ответить на него не так просто. В чем смысл понятия "лабиринт", которым пользовался Геродот, говоря о сложном и запутанном архитектурном сооружении? И что было главным в сооружении: красота или путаница? Древние греки (в Греции, как считается, хотя этот факт и оспариваемый, впервые и появился лабиринт) обозначали им и то, и другое. Правда, есть основания полагать, что эта фигура была известна людям давно — так, в местечке Лудзанас на острове Сардиния на одной из скал высечен пралабиринт, датируемый III тысячелетием до н.э.
Впрочем, в древних источниках лабиринт называется не иначе как "хорос", то есть "круг". Однако это понятие можно трактовать по разному — не только как форму здания – цирка но и как форму движения, "хоровод". Не случайно в мифах повествуется о том, что Дедал, научивший людей летать, построил этот самый лабиринт на острове Крит для дочери царя Миноса Ариадны. Это уже у Гомера в "Иллиаде". Там он повествует о пути, который есть не что иное, как преодоление одного за другим концентрических ходов лабиринта, что, по сути, напоминает танцплощадку, где девушки обучались танцам, — и там, где были всего лишь размечены основные па. Может быть, эта гипотеза не лишена смысла потому, что из все тех же мифов известно, что Тезей, выбравшись из лабиринта при помощи нити Ариадны, привез на остров Делос танец под названием "Геранос" (Журавлиный), движения которого повторяли ходы лабиринта.
![]() Но это обстоятельство нисколько не приближает нас к истине и соответственно к решению загадки: зачем придуман символ лабиринта? Одно из предположений — первоначально его узор фиксировал движения ритуального танца. Так или иначе, но вскоре сам символ перекочевал в Европу, Индию, на Яву и Суматру... Но тут возникает другой вопрос: для того, чтобы символ стал востребованным другими народами нужно, чтобы он стал для них важным. Иначе, зачем в своих святилищах воспроизводить чужие ритуалы? Какой от этого прок?!
Но это обстоятельство нисколько не приближает нас к истине и соответственно к решению загадки: зачем придуман символ лабиринта? Одно из предположений — первоначально его узор фиксировал движения ритуального танца. Так или иначе, но вскоре сам символ перекочевал в Европу, Индию, на Яву и Суматру... Но тут возникает другой вопрос: для того, чтобы символ стал востребованным другими народами нужно, чтобы он стал для них важным. Иначе, зачем в своих святилищах воспроизводить чужие ритуалы? Какой от этого прок?!
![]() Значит, лабиринт и связанный с ним танец — часть ритуала, а чему был посвящен сам ритуал? Ответа опять нет, хотя догадок предостаточно. Одна из них: лабиринт — схема орбит Солнца и планет. Но самое интересное предположение, пожалуй, такое: лабиринт — магический символ некоего посвящения. Он якобы символизирует проникновение в иной мир, более совершенный по сравнению с нашим, а путь к центру — путь постижения, путь к познанию. Достигнув этого центра, "посвященный" возвращался обратно в свой мир. У многих архаичных народов, а в более поздние времена и в некоторых тайных обществах существовали подобные ритуалы, означавшие смерть и возрождение — то есть воскресение в конце времен. Так, для индейцев хопи лабиринт — символ духовного возрождения, мистического посвящения и спасения.
Значит, лабиринт и связанный с ним танец — часть ритуала, а чему был посвящен сам ритуал? Ответа опять нет, хотя догадок предостаточно. Одна из них: лабиринт — схема орбит Солнца и планет. Но самое интересное предположение, пожалуй, такое: лабиринт — магический символ некоего посвящения. Он якобы символизирует проникновение в иной мир, более совершенный по сравнению с нашим, а путь к центру — путь постижения, путь к познанию. Достигнув этого центра, "посвященный" возвращался обратно в свой мир. У многих архаичных народов, а в более поздние времена и в некоторых тайных обществах существовали подобные ритуалы, означавшие смерть и возрождение — то есть воскресение в конце времен. Так, для индейцев хопи лабиринт — символ духовного возрождения, мистического посвящения и спасения.
![]() Понятно, почему его не было в иудаизме и в исламе. А вот в христианском мире наоборот, это важнейший мотив веры. Нет, не случайно во многих церквях Европы вплоть до XV века лабиринт служил важнейшим элементом интерьера, а до середины XVIII — элементом монастырских садов и парков. Изображение лабиринта помещалось обычно у самого входа, что как бы защищало данное место от проникновения злых духов.
Понятно, почему его не было в иудаизме и в исламе. А вот в христианском мире наоборот, это важнейший мотив веры. Нет, не случайно во многих церквях Европы вплоть до XV века лабиринт служил важнейшим элементом интерьера, а до середины XVIII — элементом монастырских садов и парков. Изображение лабиринта помещалось обычно у самого входа, что как бы защищало данное место от проникновения злых духов.
Особенно много сохранилось лабиринтов в Скандинавских странах: в Швеции их около 300, в Норвегии — более 20, в Финляндии — 141, в Дании — 31. И на островах Северной Балтии их хватает.
Но последним местом, где помнили «хоровод лабиринта», была, видимо, Страна Басков, где в районе От-Суль еще меньше ста лет назад на деревенских праздниках танцевали так называемую "Улитку", во время которой танцующие становились цепочкой и двигались, выполняя определенные "повороты" и "проходы". Цель этого танца-игры в том, чтобы, постепенно формируя узор, сбить вожака с толку, чтобы он "потерял нить" и, загнанный в угол, оказался внутри цепочки. Но и в то время уже никто не знал, откуда пошла эта традиция, и что она означала.
Знаменитые лабиринты древности
Д ревние люди изображали окружающий их мир в виде круга или концентрических окружностей, а мир мертвых - в виде спирали или лабиринта. Например, аборигены Австралии изображали на могилах лабиринты как символ переселения умершего в иной непостижимый мир.
ревние люди изображали окружающий их мир в виде круга или концентрических окружностей, а мир мертвых - в виде спирали или лабиринта. Например, аборигены Австралии изображали на могилах лабиринты как символ переселения умершего в иной непостижимый мир.
1. Пирамида фараона Аменемхета III.
В центре Фаюмской области на севере Египта один из правителей XVIII династии египетских фараонов Аменемхет III (ок. 1456-1419 до н. э.) возвел пирамиду, заупокойный храм при которой был построен в виде лабиринта.
центре Фаюмской области на севере Египта один из правителей XVIII династии египетских фараонов Аменемхет III (ок. 1456-1419 до н. э.) возвел пирамиду, заупокойный храм при которой был построен в виде лабиринта.
2. Первые рисунки лабиринтов в Египте.

Первые известные рисунки лабиринтов в Египте сохранились на печатях из Мемфиса, относящихся к эпохе строительства великих пирамид (3000 лет до н. э). Справа в лабиринте изображен фараон IV династии. Выходит, что идея лабиринта существовала в Египте задолго до сооружения лабиринта Аменемхета III.
3. Кносский лабиринт на острове Крит.
З  наете ли вы один из самых прекрасных древнегреческих мифов о победе Тесея над Минотавром?
наете ли вы один из самых прекрасных древнегреческих мифов о победе Тесея над Минотавром?
Критский царь Минос приказал знаменитому художнику и архитектору Дедалу построить лабиринт. В этот лабиринт, с бесконечными коридорами, тупиками и переходами, Минос поселил Минотавра (кровожадное существо с человеческим телом и головой быка) и потребовал у афинян, убивших его сына, раз в девять лет присылать на съедение чудовищу семерых сильнейших юношей и семерых красивейших девушек. Их отводили в лабиринт, и юные афиняне, блуждая там, становясь жертвами минотавра. Когда афиняне готовили кровавую д  ань в третий раз, сын афинского царя Эгея, Тесей, задумал освободить родной город от позорной обязанности. Вместе с очередной группой жертв Минотавра он отправился на Крит с целью убить чудовище. Дочь Миноса, Ариадна, полюбила мужественного Тесея и решила помочь ему. Она дала Тесею волшебный клубок, который помог ему найти выход из лабиринта. Привязав конец нити у входа, Тесей пошел на поиски Минотавра. Поединок закончился победой юноши, который затем, идя обратно по нити Ариадны, вышел из лабиринта и вывел оттуда всех обреченных.
ань в третий раз, сын афинского царя Эгея, Тесей, задумал освободить родной город от позорной обязанности. Вместе с очередной группой жертв Минотавра он отправился на Крит с целью убить чудовище. Дочь Миноса, Ариадна, полюбила мужественного Тесея и решила помочь ему. Она дала Тесею волшебный клубок, который помог ему найти выход из лабиринта. Привязав конец нити у входа, Тесей пошел на поиски Минотавра. Поединок закончился победой юноши, который затем, идя обратно по нити Ариадны, вышел из лабиринта и вывел оттуда всех обреченных.
В 1900 году 48-летний англичанин Артур Эванс начал раскопки на острове Крит. Гораздо больше, чем доводы науки, бывшего корреспондента газеты «  Манчестер Гардиан» воодушевляли герои греческих мифов и строки из «Одиссеи»: «Остров есть Крит посреди виноцветного моря прекрасный... Разные слышатся там языки: там находишь пеласгов, в городе Кноссе живущих... Там уж царем был Минос...». Гомер однажды уже помог археологии: Генрих Шлиман, воспользовавшись «Илиадой» как «путеводителем», сумел раскопать Трою и Микены. Эванс жаждал повторить его успех на Крите. Конечно, никто тогда не мог предположить, что под толстым слоем выжженной солнцем земли лежат руины древнейшей в Европе цивилизации. Эванс назвал ее «минойской» в честь легендарного Миноса. После сенсационных раскопок на Крите мифы не обрели плоть и кровь, как, возможно, хотелось Эвансу. Но многое в них перестало казаться только литературной случайностью. Например, то, что Зевс — отец богов и людей — родился на Крите, воспринимается теперь как вполне закономерное событие.
Манчестер Гардиан» воодушевляли герои греческих мифов и строки из «Одиссеи»: «Остров есть Крит посреди виноцветного моря прекрасный... Разные слышатся там языки: там находишь пеласгов, в городе Кноссе живущих... Там уж царем был Минос...». Гомер однажды уже помог археологии: Генрих Шлиман, воспользовавшись «Илиадой» как «путеводителем», сумел раскопать Трою и Микены. Эванс жаждал повторить его успех на Крите. Конечно, никто тогда не мог предположить, что под толстым слоем выжженной солнцем земли лежат руины древнейшей в Европе цивилизации. Эванс назвал ее «минойской» в честь легендарного Миноса. После сенсационных раскопок на Крите мифы не обрели плоть и кровь, как, возможно, хотелось Эвансу. Но многое в них перестало казаться только литературной случайностью. Например, то, что Зевс — отец богов и людей — родился на Крите, воспринимается теперь как вполне закономерное событие.
Эванс не был первым, кто пытался отыскать Кносс. Лет за 20 до него археолог-любитель Минос Калокэринос заложил несколько глубоких траншей в 5 километрах от Кандии (ныне — Ираклион). Именно здесь, на Целепи Кефала, что в переводе означает «Холм Господина», критские предания размещали Кносс. В толще земли обозначились контуры громадного сооружения. Найденные в земле предметы Калокэринос хранил в здании британского консульства в Кандии, где он работал переводчиком. Коллекция удачливого грека привлекла внимание археологов, но, заметив возросший интерес к раскопкам, турецкие хозяева Кносса резко подняли цену на землю — все работы пришлось прервать на неопределенный срок.
Лабиринт раскапывался с головокружительной для археологии скоростью. Десятки тысяч найденных предметов лежали на складах — разобраться со всеми этими сокровищами у Эванса так и недостало ни времени, ни сил. За последующие десятилетия большинство находок исчезло, на оставшихся крысы и насекомые съели этикетки, но в годы раскопок Эванс мало думал о будущем: им владело вдохновение. К его чести, надо сказать, что он не вывозил сделанные находки за пределы Греции: бесценные шедевры древнего искусства остались в музеях Крита и Афин. Не чуждый тщеславия и эпикурейского образа жизни, Эванс тем не менее тратил громадные личные средства на расширение и благоустройство раскопок, пытаясь соединить в Кноссе археологическую ценность с туристической привлекательностью. Он умер в 1935-м, в почтенном возрасте, завершив фундаментальный 4-томный труд «Дворец Миноса» и предъявив человечеству удивительную культуру, которую собственноручно извлек из исторического небытия.
 Реальный облик Дворца-Лабиринта вполне оправдывал тот миф, который сложился вокруг него. Это было колоссальное сооружение общей площадью 22 тыс. м2, имевшее как минимум 5—6 надземных уровней-этажей, соединенных проходами и лестницами, и целый ряд подземных склепов.
Реальный облик Дворца-Лабиринта вполне оправдывал тот миф, который сложился вокруг него. Это было колоссальное сооружение общей площадью 22 тыс. м2, имевшее как минимум 5—6 надземных уровней-этажей, соединенных проходами и лестницами, и целый ряд подземных склепов.
Количество помещений в нем достигало тысячи — в них можно было запросто спрятать добрый десяток Минотавров.
Архитектурный комплекс с такой сложной планировкой свидетельствовал не только о способностях «дедалов» — минойских инженеров-строителей, но и о высоком уровне развития точных и прикладных наук.
Чтобы уберечь ветхие стены Дворца от губительного воздействия солнца и дождя, Эванс, не задумываясь, укреплял их бетоном; те стены, что казались позднейшими, ломал, другие надстраивал, формируя облик Дворца в соответствии со своими представлениями. С одной стороны, он, конечно, спас Кносс, но с другой — никто теперь не знает, каким был Лабиринт на самом деле...
Минойская цивилизация не была «импортирована» на Крит и не возникла на пустом месте. Неолитический «пласт» на островах Эгейского моря — один из самых глубоких в Европе, на Крите он прослеживается до 6000 года до н.э. В 1380 году до н.э. сильнейший пожар, разбушевавшийся в Кноссе, уничтожил Лабиринт и словно поставил точку в более чем 600-летнем процветании минойской цивилизации.
Было ли это несчастным случаем, поджогом или набегом варваров — неизвестно, но Лабиринт выгорел окончательно, и вместе с ним в огне пожара как будто исчезли все те знания и мастерство, что накапливались на Крите веками. Да и сами минойцы словно растворились во мраке бесконечного Лабиринта, оставив лишь напоминание о том, что цивилизации не только рождаются, но и умирают.
4. Лабиринты в Европе.
Как уже сказано выше, лабиринт — это, возможно, часть ритуала, а чему был посвящен сам ритуал? Ответа опять нет, хотя догадок предостаточно. Самое интересное предположение, пожалуй, такое: лабиринт — магический символ некоего посвящения. Не случайно во многих церквях Европы вплоть до XV века лабиринт служил важнейшим элементом интерьера, а до середины XVIII — элементом монастырских садов и парков. Изображение лабиринта помещалось обычно у самого входа, что как бы защищало данное место от проникновения злых духов.
Мозаиками в форме лабиринтов украшены полы многих средневековых соборов Европы, например



Шартрского, Сиенского, святого Квентина и других.

Интересно отметить, что в средневековье для лабиринтов находили вполне мирные и практические применения: разбивали грядки огородов в форме лабиринтов.
В Англии знаменитым архитектурным лабиринтом была беседка Розамунды.
Надеюсь, для вас будет нетрудно найти путь к беседке, расположенной в парке, изображенном на рисунке. Быть может, для сокращения времени вам не бесполезен будет совет начать поиски от хижины, и найти лучше выход из этого коварного парка, чем начинать со входа.
К лассификация лабиринтов
лассификация лабиринтов
I. Подковообразные лабиринты - лабиринты так называемого «классического типа»:
(1) Швеция;
(2) Финляндия;
(3) Англия;
(4) Карельский полуостров, РФ.
К этой группе относятся дерново-растительные лабиринты:
(5) Англия;
(6-8) Соловецкие острова;
(9) ГДР. В центре таких сооружений непременно помещалась каменная пирамидка.
П. Круглоспиральные лабиринты:
(10), (13) Соловецкие острова;
(11) Греция;
(12) Югославия;
(14) Англия.
III. Почкообразные лабиринты - взаимно вписанные спирали:
(15) Соловецкие острова;
(16), (17) Кольский полуостров.
IV. Концентрически-круговые лабиринты:
(18) Кольский полуостров;
(19), (20) Соловецкие острова.
На этом же рисунке представлены аналоги каменных лабиринтов:
(21) подковообразный лабиринт на кносских серебряных монетах III-I вв. до н. э.;
(22) лабиринт в одном из соборов на территории Финляндии;
(23) лабиринт на северорусском скальне, Архангельская область.
Методы прохождения лабиринтов
Исследуя замысловатые лабиринтные маршруты, вы испытаете прекрасное чувство их первооткрывателя.
Первый метод – МЕТОД ПРОБ И ОШИБОК. Выбирайте любой путь, а если он заведет вас в тупик, то возвращайтесь назад и начинайте все сначала.
Второй метод – МЕТОД ЗАЧЕРКИВАНИЯ ТУПИКОВ. Начнем последовательно зачеркивать тупики, т.е. маршруты, не имеющие ответвлений и заканчивающиеся перегородкой. Незачеркнутая часть коридора будет выходом или маршрутом от входа к выходу или к центру.
Третий метод – ПРАВИЛО ОДНОЙ РУКИ. Оно состоит в том, что по лабиринту надо двигаться не отрывая одной руки (правой или левой) от стены. Это правило не универсальное, но часто полезное. Им пользуются тогда, когда все стены хотя и имеют сложные повороты и изгибы, но составляют непрерывное продолжение наружной стены. Лабиринты не должны содержать замкнутых маршрутов.
Лабиринт как игра
Лабиринты были слишком загадочным и заманчивым объектом, чтобы оказаться вне волшебного мира игр. Неизвестно только, кто раньше начал использовать их в играх. Во всяком случае, дети древних греков и римлян уже увлекались ими. Это доказывает сохранившийся на стене одного из домов Помпеи детский рисунок лабиринта и надпись возле него на латинском языке: «Лабиринт. Здесь живет Минотавр».
Перед вами несколько лабиринтов, нарисованных на бумаге. Пройти их будет не так-то просто. Захвати с собой в дорогу свою смекалку и находчивость. А еще тебе пригодятся ... твои знания по МАТЕМАТИКЕ.
-
Только одна дорога может привести Дональда и племянников к дядюшке Скруджу, бабушке Дак или Дэйзи. Что это за дорога? К кому именно она их приведет? Кружок на дороге означает, что Дональд должен повернуть направо, а звездочка – что он должен повернуть налево.
-
Около дома Ежа растет в 4 раза больше деревьев, чем около дома Кролика, и на 2 дерева больше, чем около берлоги медведя. Покажи разными цветами, как попасть к своему дому:
красным – Ежу,
синим – Кролику,
зеленым – Медведю.
Раскрась зверей, около домов которых хвойных деревьев в 2 раза меньше, чем лиственных. Нарисуй шишку рядом с домиками, над которыми хвойных деревьев на 2 меньше, чем лиственных.

-
Н
 а рисунке изображена замкнутая ломаная линия, которая образовала лабиринт. Раскрась цветным карандашом область, границей которой является этот лабиринт. Какие мыши находятся внутри области, а какие снаружи? Покажи путь, по которому должна пройти мышь А, чтобы выбраться из лабиринта. Какие еще мыши могут выбраться из лабиринта?
а рисунке изображена замкнутая ломаная линия, которая образовала лабиринт. Раскрась цветным карандашом область, границей которой является этот лабиринт. Какие мыши находятся внутри области, а какие снаружи? Покажи путь, по которому должна пройти мышь А, чтобы выбраться из лабиринта. Какие еще мыши могут выбраться из лабиринта?
В настоящее время лабиринты очень широко применяются на уроках математики. А еще это очень полезное и увлекательное занятие, которое помогает развитию воображения, логического мышления и просто смекалки!
Просмотр содержимого документа
«ot_starin»
Зачем человеку нужны измерения
Измерения - одно из важнейших дел в современной жизни. Но не всегда
было так. Когда первобытный человек убивал медведя в неравном поединке он, конечно, радовался, если тот оказывался достаточно большим. Это обещало сытую жизнь ему и всему племени на долгое время. Но он не тащил тушу медведя на весы: в то время никаких весов не было. Не было особой нужды в измерениях и когда человек делал каменный топор: технических условий на такие топоры не существовало и все определялось размером подходящего камня, который удавалась найти. Все делалось на глаз, так, как подсказывало чутье мастера.
Позднее люди стали жить большими группами. Начался обмен товарами, перешедшими потом в торговлю, возникли первые государства. Тогда появилась нужда в измерениях. Царские песцы должны были знать, какова площадь поля у каждого крестьянина. Этим определялось, сколько зерна он должен отдать царю. Надо было измерить урожай с каждого поля, а при продаже льняного мяса, вина и других жидкостей – объем проданного товара. Когда начали строить корабли, нужно было заранее наметить правильные размеры: иначе корабль затонул бы. И уж, конечно, не могли обойтись без измерений древние строители пирамид, дворцов и храмов, до сих пор поражают нас своей соразмерностью и красотой.
СТАРИННЫЕ РУССКИЕ МЕРЫ.
Русский народ создал свою собственную систему мер. Памятники X века говорят не только о существовании системы мер в Киевской Руси, но и государственном надзоре за их правильностью. Надзор этот был возложен на духовенство. В одном из уставов князя Владимира Святославовича говорится:
« …еже искони установлено есть и поручено есть епископам градские и везде всякие мерила и спуды и весы... блюсти без пакости, ни умножити, ни умалити...» (...издавна установлено и поручено епископам наблюдать за правильностью мер ... не допускать ни умаления, ни увеличения их...). Вызвана была эта необходимость надзора потребностями торговли как внутри страны, так и со странами Запада (Византия, Рим, позднее германские города) и Востока (Средняя Азия, Персия, Индия). На церковной площади происходили базары, в церкви стояли лари для хранения договоров по торговым сделкам, при церквах находились верные весы и меры, в подвалах церквей хранились товары. Взвешивания производились в присутствии представителей духовенства, получавших за это пошлину в пользу церкви
Меры длины
Древнейшими из них являются локоть и сажень. Точной первоначальной длинны той и другой меры мы не знаем; некий англичанин, путешествовавший по России в 1554 году, свидетельствует, что русский локоть равнялся половине английского ярда. Согласно «Торговой книге», составленной для русских купцов на рубеже XVI и XVII веков, три локтя были равны двум аршинам. Название «аршин» происходит от персидского слова «арш», что значит локоть.
Первое упоминание сажени встречается в летописи ХI века, составленной киевским монахом Нестором.
В более позднее времена установилась мера расстояния верста, приравненная к 500 саженям. В древних памятниках верста называется поприщем и приравнивается иногда к 750 саженям. Это может быть объяснено существованием в древности более короткой сажени. Окончательно верста к 500 саженей установилась только в XVIII веке.
В эпоху раздробленности Руси не было единой системы мер. В ХV и XVI веках происходит объединение русских земель вокруг Москвы. С возникновением и ростом общегосударственной торговли и с установлением для казны сборов со всего населения объединенной страны встает вопрос о единой системе мер для всего государства. Мера аршин, возникшая при торговли с восточными народами, входит в употребление.
В XVIII веке меры уточнялись. Петр 1 указом установил равенство трехаршинной сажени семи английским футам. Прежняя русская система мер длины, дополненная новыми мерами, получила окончательный вид:
Миля = 7 верстам (= 7,47 километра);
Верста = 500 саженям (= 1,07 километра);
Сажень = 3 аршинам = 7 футам (= 2,13 метра);
Аршин = 16 вершкам = 28 дюймам (= 71,12 сантиметр);
Фут = 12 дюймам (= 30,48 сантиметра);
Дюйм = 10 линиям (2,54 сантиметра);
Линия = 10 точкам (2,54 миллиметра).
Когда говорили о росте человека, то указывали лишь, на сколько вершков он превышает 2 аршина. Поэтому слова «человек 12 вершков роста» означали, что его рост равен 2 аршинам 12 вершкам, то есть 196 см.
Меры площадей
В «Русской правде» - законодательном памятнике, который относиться к ХI - XIII векам, употребляется земельная мера плуг. Это была мера земли, с которой платили дань. Есть некоторые основания считать плуг равным 8-9 гектарам. Как и во многих странах, за меру площади часто принимали количество ржи необходимой для засева этой площади. В ХIII- ХV веках основной единицей площади была кадь-площадь, для засева каждой нужно была примерно 24 пуда (то есть 400 кг. ) ржи . Половина этой площади, получившая название десятины стала основной мерой площади в дореволюционной России. Она ровнялась примерно 1,1 гектара. Десятина иногда называлась коробьей.
Другая единица для измерений площадей, равная половине десятины называлась (четверть) четь. В дальнейшем размер десятины был приведен в соответствие не с мерами объема и массы, а с мерами длины. В «Книге сонного письма» в качестве руководства для учета налогов с земли устанавливается десятина ровная 80*30=2400 квадратным саженям.
Налоговой единицы земли была с о х а (это количество пахотной земли, которое был в состоянии обработать один пахарь).
МЕРЫ ВЕСА (МАССЫ ) и ОБЪЕМА
Древнейшей русской весовой единицей была гривна. Она упоминается еще в договорах Х века между киевскими князьями и византийскими императорами. Путем сложных расчетов ученые узнали, что гривна весила 68,22 г. Гривна ровнялась арабской единице веса ротль. Потом основными единицами при взвешивании стали фунт и пуд. Фунт ровнялся 6 гривнам, а пуд - 40 фунтам. Для взвешивания золота применялись золотники, составлявшие 1,96 доли фунта (отсюда происходит пословица «мал золотник да дорог»). Слова «фунт» и «пуд» происходят от одного и того же латинского слова «пондус» означавшего тяжесть. Должностные лица, проверявшие весы, назывались «пундовщиками» или «весцами». В одном из рассказов Максима Горького в описании амбара кулака читаем: «На одном засове два замка - один другого пудовее (тяжелее)».
К концу XVII века сложилась система русских мер веса в следующем виде:
Ласт =72 пудам (= 1,18 т.);
Берковец = 10 пудам (= 1,64 ц);
Пуд = 40 большим гривенкам (или фунтам), или 80 малым гривенкам, или 16 безменам (= 16,38 кг.);
Первоначальные древние меры жидкости - бочка и ведро – остаются неустановленными в точности. Есть основание полагать, что ведро вмещало 33 фунта воды, а бочка – 10 ведер. Ведро делили на 10 штофов.
Денежная система русского народа
Денежными единицами у многих народов служили кусочки серебра или золота определенного веса. В Киевской Руси такими единицами были гривны серебра. В «Русской правде» - древнейшем своде русских законов говорится, что за убийство или кражу коня полагается штраф в 2 гривны, а за вола - 1 гривна. Гривну делили на 20 ногат или на 25 кун, а куну – на 2 резаны. Название «куна» (куница) напоминает о временах, когда на Руси не было металлических денег, а вместо них употреблялись меха, а позднее – кожаные деньги – четырехугольные кусочки кожи с клеймами. Хотя гривна как денежная единица давно вышла из употребления, однако слово «гривна» сохранилось. Монету достоинством 10 копеек называли гривенником. Но это, конечно, не то же самое, что старая гривна.
Чеканные русские монеты известны со времен князя Владимира Святославовича. Во времена ордынского ига русские князья были обязаны указывать на выпускаемых монетах имя правившего в Золотой Орде хана. Но после Куликовской битвы, принесшей победу войскам Дмитрия Донского над полчищами хана Мамая, начинается и освобождение русских монет от ханских имен. Сначала эти имена стали заменяться неразборчивой вязью из восточных букв, а потом совсем исчезли с монет.
В летописях, относящихся к 1381 году, впервые встречается слово «деньга». Слово это происходит от индусского названия серебряной монеты танка, которую греки называли данака, татары – тенга.
Первое употребление слова «рубль» относится к XIV веку. Слово это происходит от глагола «рубить». В XIV веке гривну стали рубить пополам, и серебряный слиток в половину гривны (= 204,76 г) получил название рубля или рублевой гривенки.
В 1535 году были выпущены монеты – новгородки с рисунком всадника с копьем в руках, получившие название копейных денег. Летопись отсюда производит слово «копейка».
Дальнейший надзор за мерами в России.
С оживлением внутренней и внешней торговли надзор за мерами от духовенства перешел к специальным органам гражданской власти – приказу большой казны. При Иване Грозном предписывается взвешивать товары только у пудовщиков.
В XVI и XVII веках усердно вводились единые государственные, или таможенные меры. В XVIII и XIX веках проводились мероприятия по усовершенствованию системы мер и весов.
Закон о мерах и весах 1842 года закончил продолжавшиеся свыше 100 лет мероприятия правительства по упорядочению системы мер и весов.
Д. И. Менделеев – метролог.
В 1892 году гениальный русский химик Дмитрий Иванович Менделеев стал во главе Главной палаты мер и весов.
Руководя работой Главной палаты мер и весов, Д.И. Менделеев полностью преобразовал дело измерений в России, наладил научно- исследовательскую работу и решил все вопросы о мерах, которые вызывались ростом науки и техники в России. В 1899 году был издан разработанный Д.И. Менделеевым новый закон о мерах и весах.
В первые годы после революции Главная палата мер и весов, продолжала традиции Менделеева, провела колоссальную работу по подготовке введения метрической системы в СССР. После некоторых перестроек и переименований бывшая Главная палата мер и весов в настоящее время существует в виде Всесоюзного научно – исследовательского института метрологии имени Д.И. Менделеева.
Французские меры
Первоначально во Франции, да и во всей культурной Европе, пользовались латинскими мерами веса и длины. Но феодальная раздробленность вносила свои коррективы. Скажем, иному сеньору приходила фантазия слегка увеличить фунт. Никто из его подданных не возразит, не восставать же из-за таких мелочей. Но если посчитать, в общем, все оброчное зерно, то какая выгода! Также и с городскими цехами ремесленников. Кому-то было выгодно уменьшать сажень, кому-то увеличивать. В зависимости от того продают они сукно или покупают. По слегка, по чуть-чуть, и вот вам уже и рейнский фунт, и амстердамский, и нюренбергский и парижский и т. д. и т. п.
А с саженями и того обстояло хуже, только на юге Франции вращалось более десятка разных единиц длины.
Правда, в славном городе Париже в крепости Ле Гран Шатель еще со времен Юлия Цезаря в крепостную стену был вделан эталон длины. Он представлял собой железный кривоколенный циркуль, ножки которого заканчивались двумя выступами с параллельными гранями, между которыми должны точно входить все имевшиеся в употреблении сажени. Сажень Шателя пробыл официальной мерой длины до 1776 года.
С первого взгляда меры длины выглядели так:
Лье морское – 5, 556 км.
Лье сухопутное = 2 милям = 3,3898 км
Миля (от лат. тысяча) = 1000 туазов.
Туаз (сажень) =1,949 метров.
Фут (ступня) =1/6 туаза = 12 дюймов = 32,484 см.
Дюйм (палец) =12 линиям = 2,256 мм.
Линия = 12 точкам = 2,256 мм.
Точка = 0,188 мм.
На самом деле, поскольку феодальные привилегии никто не отменял, все это касалось города Парижа, ну дофине, в крайнем случае. Где-нибудь в глубинке фут запросто мог определяться, как размер ступни сеньора, или как средняя длина ступней 16 человек, выходящих с заутрени в воскресенье.
Парижский фунт = ливр = 16 унциям = 289,41 гр.
Унция (1/12 фунта) = 30,588 гр.
Гран (зерно) = 0,053 гр.
А вот артиллерийский фунт до сих пор равнялся 491,4144 гр., то есть просто соответствовал нюренбегскому фунту, которым пользовался еще в 16 веке господин Гартман, один из теоретиков – мастеров артиллерийского цеха. Соответственно с традициями гуляла и величина фунта в провинциях.
Меры жидких и сыпучих тел, тоже не отличались стройным однообразием , ведь Франция была все-таки страной, где население в основном выращивало хлеб и вино.
Мюид вина = около 268 литров
Сетье – около 156 литров
Мина = 0,5 сетье = около 78 литров
Мино = 0,5 мины = около 39 литров
Буассо = около 13 литров
Английские меры
Английские меры, меры, применяемые в Великобритании, США. Канаде и др. странах. Отдельные из этих мер в ряде стран несколько различаются по своему размеру, поэтому ниже приводятся, в основном, округленные метрические эквиваленты английских мер, удобные для практических расчетов.
Меры длины
Миля морская (Великобритания) = 10 кабельтовых = 1,8532 км
Миля морская (США, с 1 июля 1954 г.) = 1,852 км
Кабельтов (Великобритания) = 185,3182 м
Кабельтов (США) = 185,3249 м
Миля уставная = 8 фарлонгам = 5280 футам = 1609,344 м
Фарлонг = 10чейнам = 201,168 м
Чейн = 4 родам = 100 линкам = 20,1168 м
Род (поль, перч) = 5,5 ярдам = 5,0292 м
Ярд = 3 футам = 0,9144 м
Фут = 3 хэндам = 12 дюймам = 0,3048 м
Хэнд = 4 дюймам = 10,16 см
Дюйм = 12 линиям = 72 точкам = 1000 милам = 2,54 см
Линия = 6 точкам = 2,1167 мм
Точка = 0,353 мм
Мил = 0,0254 мм
Меры площади
Кв. миля = 640 акрам = 2,59 км2
Акр = 4 рудам = 4046,86 м2
Руд = 40 кв. родам = 1011,71 м2
Кв. род (поль, перч) = 30,25 кв. ярдам = 25,293 м2
Кв. ярд = 9 кв. футам = 0,83613 м2
Кв. фут = 144 кв. дюймам = 929,03 см2
Кв. дюйм = 6,4516 см2
Меры массы
Тонна большая, или длинная = 20 хандредвейтам = 1016,05 кг
Тонна малая, или короткая (США, Канада и др.) = 20 центалам = 907,185 кг
Хандредвейт = 4 квортерам = 50,8 кг
Центал = 100 фунтам = 45,3592 кг
Квортер = 2 стонам = 12,7 кг
Стон = 14 фунтам = 6,35 кг
Фунт = 16 унциям = 7000 гранам = 453,592 г
Унция = 16 драхмам = 437,5 грана = 28,35 г
Драхма = 1,772 г
Гран = 64,8 мг
Единицы объема, вместимости.
Куб. ярд = 27 куб. футам = 0,7646 куб. м
Куб. фут = 1728 куб дюймам = 0,02832 куб. м
Куб. дюйм = 16,387 куб. см
Единицы объема, вместимости
для жидкостей.
Галлон (английский) = 4 квартам = 8 пинтам = 4,546 л
Кварта (английская) = 1,136 л
Пинта (английская) = 0,568 л
Единицы объема, вместимости
для сыпучих тел
Бушель (английский) = 8 галлонам (английским) = 36,37 л

Развал древних систем мер
В I-II нашей эры римляне овладели почти всем известным тогда миром и ввели Вов всех завоеванных странах свою систему мер. Но через несколько столетий Рим был завоеван германцами и созданная римлянами империя распалась на множество мелких государств.
После этого и начался развал введенной системы мер. Каждый король, а то и герцог, пытался ввести свою систему мер, а если удавалось то и денежных единиц.
Развал системы мер достиг наивысшей точки в XVII-XVIII веках, когда Германия оказалось раздробленной на столько государств, сколько дней в году, в результате этого в ней насчитывалось 40 различных футов и локтей, 30 различных центнеров, 24 различных мили.
Во Франции было 18 единиц длины, называвшихся лье, и т.д.
Это вызывало затруднение и в торговых делах, и при взимании налогов, и в развитии промышленности. Ведь действовавшие одновременно единицы меры не были связаны друг с другом, имели различные подразделения на более мелкие. В этом было трудно разобраться многоопытному купцу, а что уж тут говорить о неграмотном крестьянине. Разумеется, этим пользовались купцы и чиновники, чтобы грабить народ.
В России в разных местностях почти все меры имели различные значения, поэтому в учебниках арифметики до революции помещали подробные таблицы мер. В одном распространенном дореволюционном справочнике можно было найти до 100 различных футов, 46 различных миль, 120 различных фунтов и т.д.
Потребности практики заставили начать поиски единой системы мер. При этом было ясно, что надо отказаться от установления между единицами измерения и размерами человеческого тела. И шаг у людей бывает разный и длина ступни у них неодинакова, и пальцы у них разной ширины. Поэтому надо было искать новые единицы измерения в окружающей природе.
Первой попытки найти такие единицы были сделаны еще в древности в Китае и в Египте. Египтяне в качестве единицы массы выбрали массу 1000 зерен. Но и зерна бывают неодинаковы! Поэтому идея одного из китайских министров, предложившего задолго до нашей эры выбрать в качестве единицы 100 расположенных в ряд зерен красного сорго, тоже была неприемлемой.
Ученые выдвигали разные идеи. Кто предлагал взять за основы мер размеры, связанных с пчелиными сотами, кто путь, проходимый за первую секунду, свободно падающим телом, а знаменитый ученный XVII века Христиан Гюйгенс предложил взять третью часть длины маятника, делающегося одно качание в секунду. Эта длина весьма близка к двойной длине вавилонского локтя.
Еще до него польский ученый Станислав Пудловский предложил взять за единицу измерения длину самого секундного маятника.
Рождение метрической системы мер.

Не удивительно, что когда в восьмидесятых годах XVIII купцы нескольких французских городов обратились к правительству с просьбой об установлении единой для всей страны системы мер, ученые тут же вспомнили о предложении Гюйгенса. Принятию этого предложения помешало то, что длина секундного маятника различна в различных местах земного шара. На Северном полюсе она больше, а на экваторе меньше.
В это время во Франции произошла буржуазная революция. Было созвано Национальное собрание, которое создало при Академии наук комиссию, составленную из крупнейших французских ученых того времени. Комиссии предстояло выполнять работу по созданию новой системы мер.
Одним из членов комиссии был знаменитый математик и астроном Пьер Симон Лаплас. Для его научных изысканий было весьма важно знать точную длину земного меридиана. Кто-то из членов комиссии вспомнил о предложении астронома Мутона взять за единицу длины часть меридиана, равную одной 21600–й части меридиана. Лаплас тут же поддержал это предложение (а может быть, и сам натолкнул на это мысль остальных членов комиссии). Сделали только одно измерение. Для удобства решили принять за единицу длины одну сорокамиллионную часть земного меридиана. Это предложение было внесено на рассмотрение национального собрания и принято им.
Все остальные единицы были согласованы с новой единицей, получившей название метра. За единицу площади был принят квадратный метр, объем – кубический метр, массы – масса кубического сантиметра воды при определенных условиях.
В 1790 году Национальное собрание приняло декрет о реформе систем мер. В представленном Национальному собранию докладе отмечалось, что в проекте реформы нет ничего произвольного, кроме десятичной основы, и нет ничего местного. «Если память об этих работах утратилось и сохранились лишь одни результаты, то в них не нашлось бы никакого признака, по которому можно было узнать, какая нация затеяла план этих работ, и осуществила их», - говорилось в докладе. Как видно, комиссия Академии, стремилась к тому, чтобы новая система мер не дала повода какой –нибудь нации отвергать систему, как французскую. Она стремилась оправдать лозунг: «На все времена, для всех народов», который был провозглашен позднее .
Уже в апреле 17956 года был утвержден закон о новых мерах, для всей Республики введен единый эталон : платиновая линейка на которой начертан метр .
Комиссия Парижской Академии наук с самого начала работ по разработке н6овой системы установила, что отношения соседних единиц должно равняться 10 .Для каждой величины (длина, масса, площадь, объем) от основной единицы этой величины образуются другие, большие и меньшие меры одинаковым образом (за исключением, названий «микрон», «центнер», «тонна»). Для образования названий мер, больших основной единицы, к названию последней с переде прибавляются греческие слова: «дека»-«десять», «гекто»- «сто», «кило»-«тысяча», «мириа»-«десять тысяч»; для образования названия мер , меньших основной единицы, прибавляются, также спереди частицы : «деци»-«десять», «санти»-«сто», «милли»-«тысяча».
Архивный метр.

Закон 1795 года, установив временный метр, указывает, что работы комиссии будут продолжаться. Измерительные работы были закончены лишь к осени 1798 года и дали окончательную длину метра в 3 фута 11,296 линии вместо 3футов 11,44 линии, каковую длину имел временный метр 1795 года (старинный французский фут равнялся 12 дюймам, дюйм-12 линиям).
Министром иностранных дел Франции был в те годы выдающийся дипломат Талейран, который еще раньше занимался проектом реформы, он предложил созвать представителей союзных с Франции и нейтральных стран для обсуждения новой системы мер и предания ее международного характера. В 1795 году делегаты съехались на международной конгресс; на нем было объявлено об окончании работ по проверке определения длины основных эталонов. В том же году изготовлены окончательные прототипы метры и килограммы. Они были изданы в Архив Республики на хранение, по этому получили названия архивный .
Временный метр был отменен и вместо него единицы длины признан архивный метр. Он имел вид стержня, поперечное сечение которого напоминает букву Х. Архивные эталоны лишь через 90 лет уступили свое место новым, получившим название международных.
Причины, мешавшие проведению в жизнь
метрической системы мер.
Население Франции встретило новые меры без особого энтузиазма. Причиной такого отношения были отчасти самые новые единицы мер не соответствовавшие вековым привычкам, а также новые, непонятные населению название мер.
Среди лиц, относившихся к новым мерам без восторга, был и Наполеон. Декретом 1812 года он наряду с метрической системой ввел «обиходную» систему мер для употребления в торговле.
Восстановление во Франции в 1815 году королевской власти содействовало забвенью метрической системы. Революционное происхождение метрической системы мешало распространению ее в других странах.
С 1850 года передовые ученные начинают энергичную агитацию в пользу метрической системы .Одной из причин этого были начавшиеся тогда международные выставки, показавшие все удобства существовавших различных национальных систем мер. Особенно плодотворно в этом направлении была деятельность Петербургской Академии наук и ее члена Бориса Семеновича Якоби. В семидесятых годах эта деятельность увенчалась действительным превращением метрической системы в международную.
Метрическая система мер в России.
В России ученые с начала XIX века поняли назначение метрической системы и пытались ее широко внедрить в практику.
В годы от 1860 до 1870 после энергичных выступлений Д.И.Менделеева компанию в пользу метрической системы ведут академик Б.С.Якоби, профессор математики А.Ю.Давидов автор распространенных в свое время школьных учебников математики, и академик А.В. Гадолин. К ученым присоединялись и русские фабриканты и заводчики. Русское техническое общество поручило специальной комиссии под председательством академика А.В. Гадолина разработать этот вопрос. В эту комиссию поступило много предложений от ученных и технических организаций, единогласно поддерживающих предложения о переходе на метрическую систему.
Изданный в 1899 году закон о мерах и весах разработанный Д.Т.Менделеевым включал параграф № 11:
«Международный метод и килограмм, их подразделения, а равно и иные метрические меры дозволяется применять в России, наверняка с основными российскими мерами, в торговых и иных сделках, контрактах, сметах, подрядах, и тому подобных – взаимному соглашению договаривающихся сторон, а также в пределах деятельности отдельных казенных ведомств…с разращения или по распоряжению подлежащих министров…».
Окончательное решение вопроса о метрической системы в России получил уже после Великой Октябрьской социалистической революции. В 1918 году Советом Народных Комиссаров под председательством В.И.Ленина было издано постановление, в котором предлагалось :
«Положить в основание всех измерений международную метрическую систему мер и весов десятичными подразделениями и производными.
Принять за основу единицы длины - метр, а за основу единицы веса (массы) - килограмм. За образцы единиц метрической системы принять копию международного метра, носящую знак № 28, и копию международного килограмма, носящую знак № 12, изготовленные из иридистой платины, переданные России Первой международной конференцией мер и весов в Париже в 1889 году и хранимые ныне в Главной палате мер и весов в Петрограде».
С 1 января 1927 года, когда переход промышленности и транспорта на метрическую систему был подготовлен, метрическая система мер стала единственно допускаемой в СССР системой мер и весов.
Старинные русские меры
в пословицах и поговорках.
Аршин да кафтан, да два на заплатки.
Борода с вершок, а слов с мешок.
Врать - семь верст до небес и все лесом.
За семь верст комара искали ,а комар на носу.
На аршин бороды, да ума на пядь.
На три аршина в землю видит!
Ни пяди не уступлю.
От мысли до мысли пять тысяч верст.
Охотник за семь верст ходит киселя хлебать.
Писать (говорить) о чужих грехах аршинными, а о своих - строчными буквами.
Ты от правды (от службы) на пядень, а она от тебя – на сажень.
Тянись верстой, да не будь простой.
За это можно и пудовую (рублевую) свечку поставить.
Зернышко пуд бережет.
Не худо, что булка с полпуда.
Одно зерно пуды приносит.
Свой золотник чужого пуда дороже.
Съел полпуда – сыт покуда.
Узнаешь почем пуд лиха.
У него в голове ни ползолотника мозга (ума).
Худое валит пудами, а хорошее золотниками.
ТАБЛИЦА СРАВНЕНИЯ МЕР
-
Меры длины
1 верста = 1,06679 километра
1 сажень = 2,1335808 метра
1 аршин = 0,7111936 метра
1 вершок = 0,0444496 метра
1 фут = 0,304797264 метра
1 дюйм = 0,025399772 метра
1 километр = 0,9373912 версты
1 метр = 0,4686956 сажени
1 метр = 1,40609 аршина
1 метр = 22,4974 вершка
1 метр = 3,2808693 фут
1 метр = 39,3704320 дюйма
-
1 сажень = 7 футов
1 сажень = 3 аршина
1 сажень = 48 вершков
1 миля = 7 верст
1 верста = 1,06679 километра
-
Меры объема и площади
1 четверик = 26,2384491 литра
1 четверть = 209,90759 литра
1 ведро = 12,299273 литра
1 десятина = 1,09252014 гектара
1 литр = 0,03811201 четверика
1 литр = 0,00952800 четверти
1 литр = 0,08130562 ведра
1 гектар = 0,91531493 десятины
-
1 бочка = 40 ведер
1 бочка = 400 штофов
1 бочка = 4000 чарок
1 четверть = 8 четвериков
1 четверть = 64 гарнца
-
Меры веса
1 пуд = 16,3811229 килограмма
1 фунт = 0,409528 килограмм
1 золотник = 4,2659174 грамма
1 доля = 44,436640 миллиграмма
-
1 килограмм = 0,9373912 версты
1 килограмм = 2,44183504 фунта
1 грамм = 0,23441616 золотника
1 миллиграмм = 0,02250395 доли -
1 пуд = 40 фунтов
1 пуд = 1280 лотов
1 берков = 10 пудов
1 ласт = 2025 и 4/9 килограмм
-
Денежные меры
-
рубль = 2 полтинам
полтина = 50 копейкам
пятиалтынный = 15 копейкам
алтын = 3 копейкам
гривенник = 10 копейкам -
2 деньги =1копейке
грош = 0.5 копейки
полушка = 0.25 копейки

15
Полезное для учителя






















