Стереометрия. Из опыта работы по подготовке к ЕГЭ

Подготовка учащихся к итоговой аттестации по математике: эффективные методы, формы и средства обучения

Стетеометрия

Бабошкина Любовь Юрьевна

учитель математики МОУ «СОШ № 55»

г. Саратова

Хорошая подготовка по планиметрии

Успешное изучение стереометрии

Лучше 1 раз увидеть, чем 100 раз услышать!

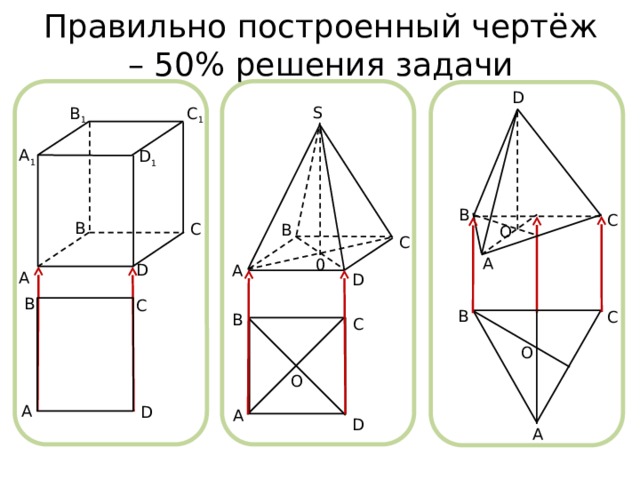
Правильно построенный чертёж – 50% решения задачи

D

S

C 1

B 1

A 1

D 1

B

C

В

С

В

O

С

A

0

D

А

А

D

В

С

B

C

В

С

O

O

А

D

А

D

A

3

Задачи на готовых чертежах

Дают возможность освежить в памяти уже изученные геометрические понятия и факты

Помогают отработать новые

Готовят учащихся к решению задач из банка задач ЕГЭ

Е.М. Рабинович «Математика. Задачи и упражнения на готовых чертежах» 7 – 9 классы

Е.М. Рабинович «Математика. Задачи и упражнения на готовых чертежах»

10 – 11 классы

Э.Н. Балаян «Геометрия. Задачи на готовых чертежах для подготовки к ЕГЭ» 10 – 11 классы

Большую часть этого пособия составляют задачи на готовых чертежах

Подборки однотипных задач для регулярного повторения во время «устного счёта»

Готовые чертежи к опорным задачам по геометрии (планиметрии и стереометрии)

Многопараметрические задачи

Для отработки одной большой темы стереометрии, например, «Углы между плоскостями»

Для итогового повторения и подготовки к ЕГЭ (при их решении повторяется большая часть курса стереометрии и планиметрии)

Задачи для выработки навыков по теме

Задачи для итогового повторения

D

а) высоту треугольника, лежащего в основании пирамиды; площадь основания; радиус окружности, вписанной в основание; радиус окружности, описанной около основания; объём пирамиды;

б) боковое ребро и апофему пирамиды; площадь боковой грани и площадь боковой поверхности пирамиды; радиус окружности, вписанной в боковую грань и радиус окружности, описанной около боковой грани;

в) плоский угол при вершине пирамиды;

г) угол между боковым ребром и стороной основания;

д) угол между боковым ребром и плоскостью основания;

е) двугранный угол , образованный боковой гранью и плоскостью основания пирамиды;

ж) двугранный угол, образованный двумя боковыми гранями пирамиды;

з) радиус сферы вписанной в пирамиду; радиус сферы, описанной около пирамиды;

и) расстояние от центра основания до боковой грани; угол и расстояние между боковым ребром и скрещивающейся с ним стороной основания; и т.д.

B

C

O

A

Задача. В правильной треугольной пирамиде сторона основания равна 6 см, высота пирамиды равна 8 см. Найдите:

14

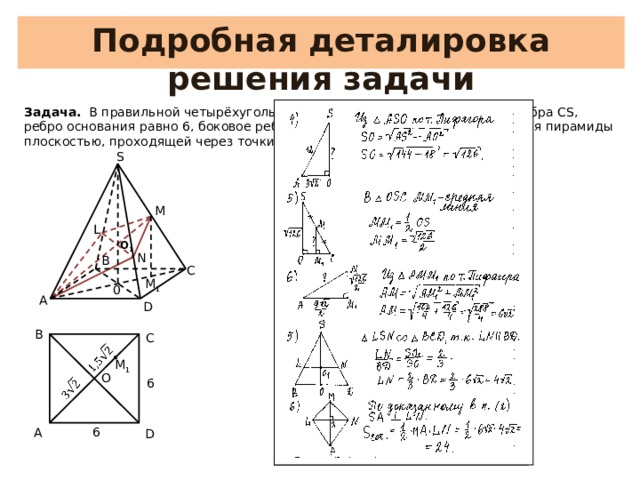
Подробная деталировка решения задачи

Задача. В правильной четырёхугольной пирамиде SАВСD N – середина ребра CS, ребро основания равно 6, боковое ребро равно 12. Найдите площадь сечения пирамиды плоскостью, проходящей через точки А и М параллельно прямой ВD.

S

М

L

О 1

N

В

С

М 1

0

А

D

В

С

М 1

O

6

6

А

D

Некоторые приёмы, облегчающие подсчёты при решении геометрических задач первой части ЕГЭ

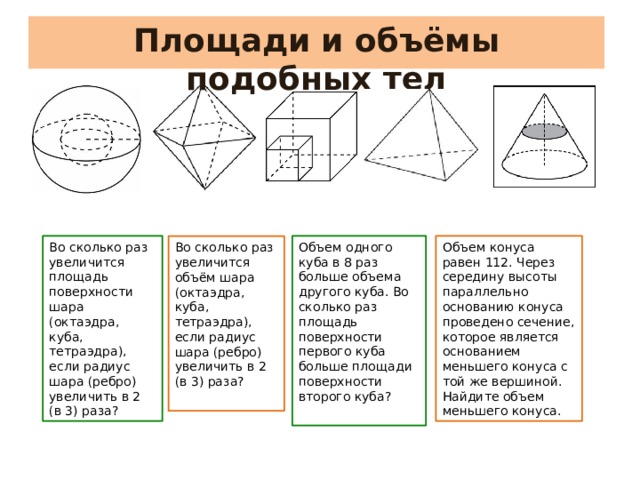
Площади и объёмы подобных тел

Во сколько раз увеличится площадь поверхности шара (октаэдра, куба, тетраэдра), если радиус шара (ребро) увеличить в 2 (в 3) раза?

Объем конуса равен 112. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Во сколько раз увеличится объём шара (октаэдра, куба, тетраэдра), если радиус шара (ребро) увеличить в 2 (в 3) раза?

15

Составные многогранники

1) являющиеся прямыми призмами

2)разделяющиеся сечением на две прямые призмы

3)многогранники с «вмятиной»

№ 1 Найдите площадь поверхности многогранника, у которого все двугранные углы прямые.

2

4

2

3

5

Расстояние между основаниями

Нарисуем основание в натуральную величину на клетчатой бумаге и по клеткам посчитаем его площадь

h =

S основания = 8, Р основания = 14,

S боковой п. = Р основания  h =14  5 = 70,

S поверхности = 2S основания + S боковой п. = 2  8 + 70 = 86

2

2

3

3

6

S основания = 22, Р основания = 22,

S боковой п. = Р основания  h = 22  3 = 66,

S поверхности = 2S основания + S боковой п. = 2  22 + 66 = 110

5

4

4

2

1

S основания = 14, Р основания = 18,

S боковой п. = Р основания  h = 18  5 = 90,

S поверхности = 2S основания + S боковой п. = 2  18 + 90 = 126

7

1

5

1

2

S основания = 33, Р осн. внешний = 24, Р осн. внутренний = 6

S бок. внешн. = Р осн. внешний  h = 24  1 = 24,

S бок. внутрен. = Р осн. внутренний  h = 6  1 = 6,

S поверхности = 2S основания + S бок. внешн. + S бок. внутрен .= 66+24+6=96

№ 2 Найдите площадь и поверхность составного многогранника

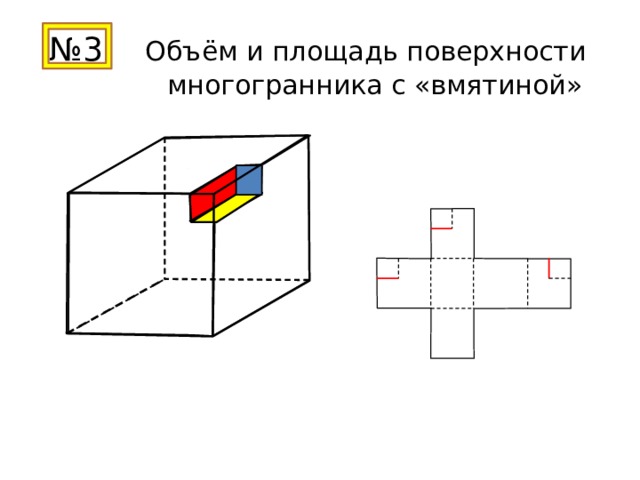
№ 3 Объём и площадь поверхности многогранника с «вмятиной»

Использованная литература

1. Балаян Э.Н. Геометрия: задачи на готовых чертежах для подготовки к ЕГЭ: 10 – 11 классы/ Э.Н. Балаян. – Ростов н/Д: Феникс, 2013. – 217 с.: ил. – (Большая перемена).

2. Вольфсон Б.И. Геометрия. Все виды заданий ГИА-9 и ЕГЭ. Решаем задачи – повторяем теорию: учебное пособие / Б.И. Вольфсон. – Ростов н/Д: Легион, 2013. – 96 с. – (Готовимся к ЕГЭ.)

3. Потоскуев Е.В. ЕГЭ. Геометрия. Задания 14, 16. Опорные задачи по геометрии. Планиметрия. Стереометрия./ Е.В. Потоскуев. – М.: Издательство «Экзамен», 2016. – 223 с. (Серия «ЕГЭ. Полный курс»)

4. Потоскуев Е.В. Геометрия. 10 кл. : задачник для общеобразоват. учреждений с углубл. и профильным изучением математики./ Е.В. Потоскуев, Л.И. Звавич. – 4-е изд., стереотип. – М.: Дрофа, 2008. – 250 с.: ил.

5. Рабинович Е.М. Задачи и упражнения на готовых чертежах. 7 – 9 классы. Геометрия./Е.М. Рабинович – М.: Илекса, 2004. – 56 с.

6. Рабинович Е.М. Задачи и упражнения на готовых чертежах. 10 – 11 классы. Геометрия./ Е.М. Рабинович – М.: Илекса, 2004. – 80 с.

7. Смирнова И.М. Геометрия. Расстояния и углы в пространстве./ И.М. Смирнова, В.А. Смирнов. – 3-е изд. перераб. и доп. – М.: Издательство «Экзамен», 2011. – 158 с. (Серия «ЕГЭ. 100 баллов»)

8. Ященко И.В. ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент». Базовый и профильный уровни / И.В. Ященко и др. – М. Издательство «Экзамен», 2016. – 640 с. (Серия «Банк заданий ЕГЭ»)