Стобальный вариант 3.по математике в формате ЕГЭ 10 класс

Стобальный вариант 3.по математике в формате ЕГЭ 10 класс

Задание 1. Задачу №1 правильно решили 13230 человек, что составляет 42% от выпускников города. Сколько всего выпускников в этом городе?

Задание 2. На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линиями.

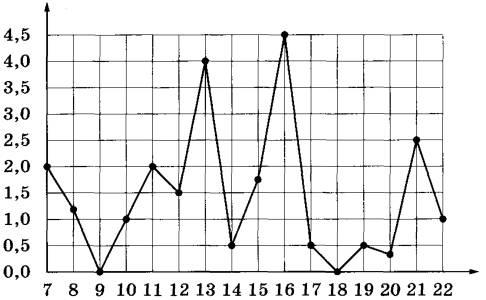
Определите по рисунку наибольшее суточное количество осадков в Мурманске за данный период. Ответ дайте в миллиметрах.

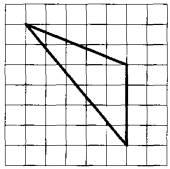
Задание 3. На клетчатой бумаге с размером клетки 1x1 изображён треугольник. Найдите его площадь.

Задание 4. По отзывам покупателей Михаил Михайлович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,81. Вероятность того, что этот товар доставят из магазина Б, равна 0,93. Михаил Михайлович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.

Задание 5. Найдите корень уравнения 

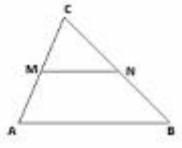
Задание 6. Площадь треугольника ABC равна 36 см2. MN - его средняя линия. Найдите площадь треугольника MNC.

Задание 7. Найдите длину промежутка возрастания функции

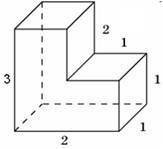
Задание 8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Задание 9. Найдите значение выражения 

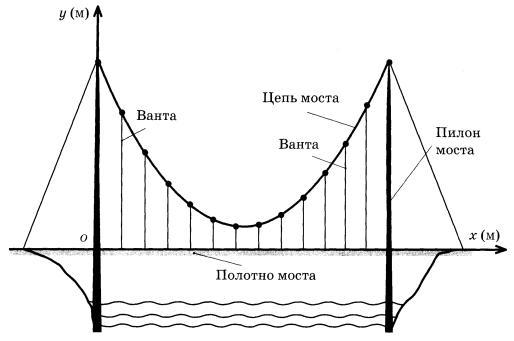
Задание 10. Самые красивые мосты — вантовые. Вертикальные пилоны связаны огромной провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами.

На рисунке изображена схема одного вантового моста. Введём систему координат: ось Оу направим вертикально вдоль одного из пилонов, а ось Ох направим вдоль полотна моста, как показано на рисунке. В этой системе координат цепь моста имеет уравнение  , где х и у измеряются в метрах. Найдите длину ванты, расположенной в 100 метрах от пилона. Ответ дайте в метрах.

Задание 11. Из пункта А в пункт В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 12 км/ч, а вторую половину пути — со скоростью 72 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 45 км/ч. Ответ дайте в километрах в час.

Задание 12. Найдите наименьшее значение функции

Задание 13. а) Решите уравнение а) Решите уравнение  .

б) Укажите корни этого уравнения, принадлежащие отрезку [4π; 11π/2].

Задание 14. Ребра правильного тетраэдра равны 42. Через середины четырех ребер проведено сечение.

А) Докажите, что сечение прямоугольник.

Б) Найдите площадь сечения.

Задание 15. Решите неравенство  .

Задание 16. Окружность с центром О касается боковой стороны АВ равнобедренного треугольника ABC, продолжения боковой стороны АС и продолжения основания ВС в точке N. Точка М — середина основания ВС.

а) Докажите, что AN = ОМ.

б) Найдите ОМ, если стороны треугольника ABC равны 10, 10 и 12.

Задание 17. 31 декабря 2014 года Арсений взял в банке 1 млн рублей в кредит. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на определённое количество процентов), затем Арсений переводит очередной транш. Арсений выплатил кредит за два транша, переведя в первый раз 550 тыс. рублей, во второй 638,4 тыс. рублей. Под какой процент банк выдал кредит Арсению?

Задание 18. Найдите все значения а, при каждом из которых уравнение имеет один корень (2х²-6х+а²+6)²=8а²(х²-3х+3).

Задание 19. Учитель пишет примеры на сложение трёх натуральных чисел так, чтобы во всех примерах ответ был один и тот же N, при этом он хочет, чтобы все слагаемые во всех примерах (даже в различных примерах) были различны.

а) Можно ли написать два таких примера, если N = 12?

б) Можно ли написать 5 таких примеров, если N = 40?

в) Можно ли написать 10 таких примеров, если N = 40?