Сценарий урока "Введение в алгебру логики"

Государственное бюджетное профессиональное

образовательное учреждение Московской области

Авиационный техникум имени В. А. Казакова»

ФИЛИАЛ

Методическая разработка

«Сценарий урока «Введение в двузначную алгебру логики»

Преподаватель специальных дисциплин:

Седова О.Б.

Раменское , 2018 г

Сценарий урока «Введение в двузначную алгебру логики»

1. Изложение нового материала

Учитель: Тема нашего урока «Введение в алгебру логики». Вам о чем-то эти слова говорят?

Студенты: приводят фразы «логически мыслить», «железная логика», «нестандартное логическое мышление» и пытаются объяснить их.

Учитель: Что же такое логика?

Логика - наука о формах, методах и законах человеческого мышления, формализуемых с помощью логического языка – системы обозначений, операций, отношений и т.п.

Формы мышления:

1. понятие

2. высказывание

3. умозаключение

Понятие — форма мышления, в которой отражаются существенные отличительные признаки объектов.

Учитель: Например, существенные признаки квадрата – равенство длин всех сторон, наличие прямых углов. Приведите примеры вы.

Студенты: приводят примеры.

Высказывание (суждение) — форма мышления, в которой что-либо утверждается или отрицается о предметах, их свойствах, или отношениях.

Учитель: Например, нет такого лабиринта, из которого не было бы выхода. Или: что с возу упало, то пропало. Теперь вы.

Студенты: приводят примеры.

Учитель: Основой суждения является логическое выражение.

Логическое выражение — конструкция, результатом вычисления которой является суждение типа «истина» или «ложь».

Учитель: Как мы уже заметили, математические выражения состоят из операндов: (чисел, переменных), соединённых знаками арифметических операций. Каких?

Студенты: приводят арифметические операции: +, -, *, /.

Учитель: А что является операндом для логической конструкции? И помощью каких операций они соединяются?

В качестве операндов логического выражения выступают высказывания , которые соединяются знаками логических операций.

Учитель: Еще одна форма человеческого мышления – это умозаключение

Умозаключение — форма мышления, посредством которой из одного или нескольких высказываний мы по определенным правилам вывода получаем новое суждение (заключение).

Учитель: Например, есть два высказывания:

«Все, что требует мужества и героизма, есть подвиг»

«Первый полет человека в космос требовал мужества и героизма». Умозаключение: Первый полет человека в космос есть подвиг.

Теперь попробуйте вы:

«Углеводороды есть органические соединения»

«Метан — углеводород»

Студенты: Умозаключение: Метан — органическое соединение.

Учитель: Во всех наших суждения, умозаключениям присутствует здравый смысл, т.е. мы понимаем о чем говорим. Но зачастую объектом изучения или применения является суждение, в котором важна не суть мысли, а ее форма. Например, рассмотрим решение квадратного уравнения:

– конкретное уравнение

– формальная запись

– формальная запись

D – формальная запись формальной записи.

Или при передаче какого-либо текста по КС, он преобразуется в форму электрических сигналов (ЭВМ «не понимает» русского языка), а мы в свою очередь описываем протекающие в ЭВМ процессы – 1и 0, логическими функциями.

Форма́льная ло́гика — наука о правилах преобразования высказываний, сохраняющих их истинностное значение безотносительно к содержанию входящих в эти высказывания понятий, а также конструирование этих правил.

Учитель: приведите формальную запись развернутой формы целого числа

Студенты:

Суждение, представленное в форме какой – либо переменной, называется логической переменной.

Учитель: Т.о. можно сделать вывод, что

логические величины делят на:

• постоянные;

• переменные

Логические константы могут принимать только два состояния: ЛОЖЬ и ИСТИНА или TRUE и FALSE или 1 и 0.

Логические переменные обозначаются символическими именами: А, В, С и т.д.

Учитель: Итак, любое суждение можно облечь в какую либо форму. Но как связать два или несколько суждений в одно и записать это? Этим вопросом занимается такой раздел логики как математическая логика.

Математическая логика изучает логические связи и отношения между суждениями с использованием языка математики (функциональные зависимости) – логические функции.

Алгебра логики – раздел математической логики, изучающий логические операции над высказываниями.

Двузначная алгебра логики занимается исчислениями над высказываниями, которые могут быть только истинными или ложными.

Двузначную алгебру высказываний интересуют два вопроса:

1. Как из простых высказываний образуются сложные.

2. Как зависит значение истинности сложного высказывания от значений истинности простых высказываний, его образующих.

Для логических функций с двумя переменными известны 16 элементарных логических функций, из которых образуются сложные логические функции.

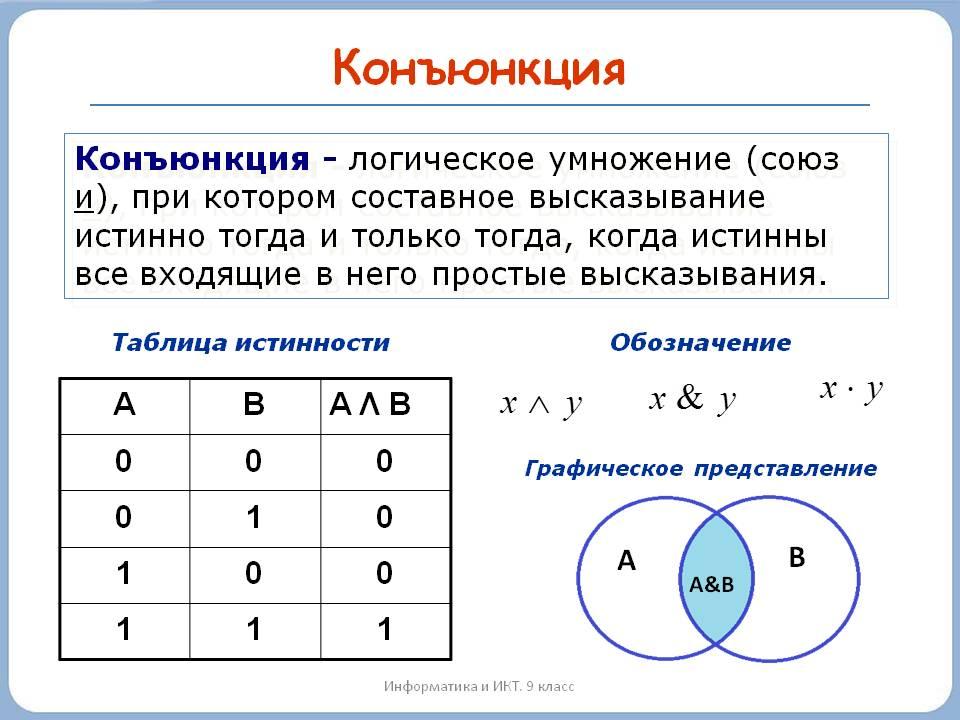
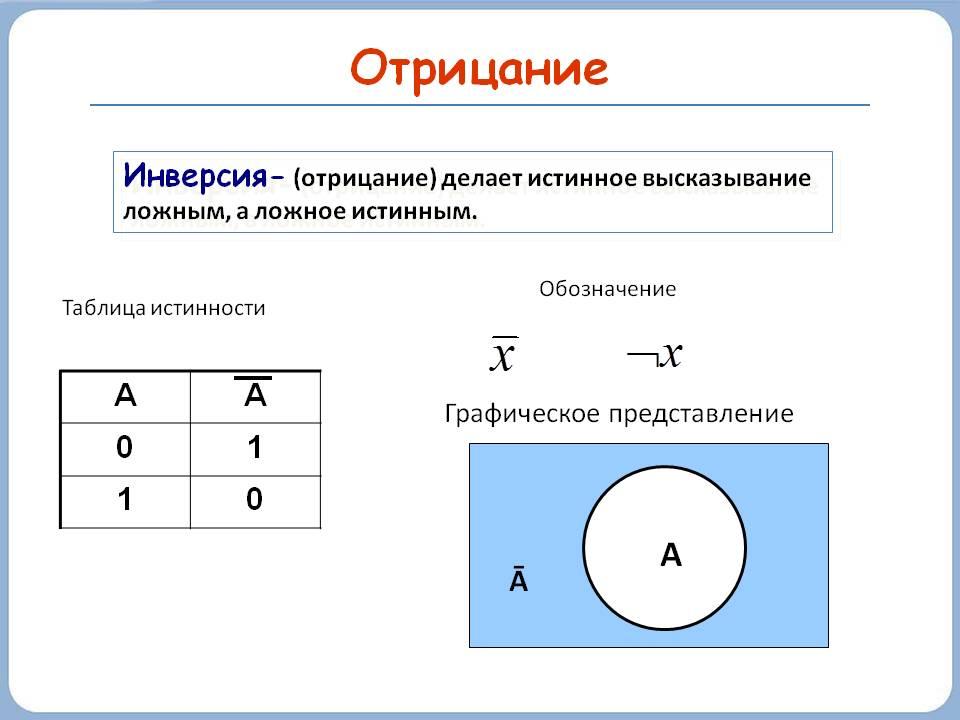
Существует 16 элементарных логических функций двух переменных. Мы познакомимся сегодня с тремя такими функциями: конъюнкцией, дизъюнкцией, инверсией.

Значение истинности каждой элементарной логической функции описывается таблицей истинности.

Логические операции элементарных логических функций можно изобразить графически.

1. Конъюнкция - логическое умножение, пересечение двух множеств

1. Дизъюнкция - логическое сложение, объединение двух множеств

1. Инверсия – логическое отрицание

Приоритет выполнение операций:

1. инверсия

2. конъюнкция

3. дизъюнкция

Из простых логических функций (высказываний) образуются сложные функции (сложные высказывания), истинность которых устанавливается также с помощью таблиц истинности.

1. Закрепление нового материала:

Решение задач:

Задача №1: В следующих высказываниях выделите простые высказывания. Запишите с помощью переменных и знаков логических операций каждое высказывание:

1. Число 376 четное и трехзначное

2. Зимой дети катаются на коньках или лыжах

3. Новый год мы встретим на даче или на Красной площади

4. Неверно, что Солнце движется вокруг Земли

5. Земля имеет форму шара, который из космоса кажется голубым

Задача №2: Пусть А= «Ане нравятся уроки информатики», В= «Ане нравятся уроки химии». Выразите следующие формулы на обычном языке:

1. A&B

2. A&B

3. A&B

4. AB

5. AB

8. AB

9. ( A&B)

10. ( AB)

11. ( A&B)

2. Задача №3: Из двух простых высказываний постройте сложное, используя логические операции «И», «ИЛИ» :

1. Марина старше Светы. Оля старше Светы.

2. Слова в этом предложении начинаются на букву «Ч». Слова в этом предложении начинаются на букву «А».

3. Часть туристов любит чай. Остальные туристы любят молоко

4. В кабинете есть учебники. В кабинете есть справочники.

5. Х=3. Х2

6. Одна половина класса изучает английский язык. Вторая половина класса изучает немецкий язык.

1. Задача №4

1. 

2. Задача №5