 МБОУ «Золотухинская средняя
МБОУ «Золотухинская средняя
общеобразовательная школа»
Сценарий занятия предметного курса «Математический практикум»
Теорема Пифагора
в задачах реальной математики
Подготовили:
Алдохина Полина,
Гоменюк Екатерина, обучающиеся 9 Б класса,
Семенихина Людмила
Михайловна, учитель математики МБОУ «Золотухинская средняя общеобразовательная школа», высшая квалификационная категория
Февраль, 2016г.
Тема занятия «Теорема Пифагора в задачах реальной математики»
Образовательная цель занятия: повторение теоремы Пифагора; закрепление умений и навыков по применению теоремы Пифагора к решению задач; существенное расширение круга геометрических задач, решаемых школьниками; подготовка к ОГЭ.
Деятельностная цель: создать условия для совершенствования навыков решения задач на применение теоремы Пифагора из раздела «Реальная математика» ОГЭ.
Результат деятельности учащихся:
Личностные УУД: формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
Метапредметные УУД:
Регулятивные: понимать учебную задачу занятия, уметь самостоятельно планировать пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных задач, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения.
Познавательные: осуществлять логические действия, формулировать ответы на вопросы.
Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве.
Методы обучения: Репродуктивный. Наглядный. Проблемно-поисковый. Эвристическая беседа. Подводящий диалог.
Оборудование:
мультимедийное оборудование для просмотра презентации,
интерактивная доска INTER WRITE Dual Board,
Система тестирования ActivExpression,
сборник задач «Теорема Пифагора в задачах реальной математики»,
карточки с высказываниями Пифагора.
Ход занятия.
Учитель. Добрый день, ребята! У нас очередное занятие по подготовке к ОГЭ, и сегодня мы продолжим путешествие по заданиям из раздела «Реальная математика». Путешествовать будем на сверхскоростном самолете, потому что время у нас ограничено – 45 минут. Но чтобы попасть в самолет, мне нужно проверить нашу готовность, а заодно узнаем, куда мы с вами отправляемся. Итак, проверим, какой багаж знаний вы взяли с собой из дома.
Устный счет (Слайд №1).
Вычислить:
52 = 25
32 = 9
102 = 100
(4 2 = 42(
2 = 42( 2 = 16·2 = 32
2 = 16·2 = 32

Кроссворд (Интерактивная презентация)
1.Равенство двух отношении (пропорция).
2.Отношение прилегающего катета к гипотенузе в прямоугольном треугольнике. (косинус).
3.Древнегреческий ученый, живший в 6.в.до н.э.(Фалес).
4.Сторона прямоугольного треугольника. (катет).
5.Сторона прямоугольного треугольника, лежащая против прямого угла. (гипотенуза)
6.Перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону. (высота)
7.Треугольник с прямым углом. (прямоугольный).

По вертикали у на слово «Пифагор». Давайте попробуем сформулировать тему и цель занятия. (Рассмотрим задачи из раздела «Реальная математика» на применение теоремы Пифагора). Да, действительно, сегодня мы будем совершенствовать навыки решения задач из раздела «Реальная математика» на применение теоремы Пифагора. Тема занятия: Теорема Пифагора в задачах реальной математики. Задание №17. А кто у нас знает почти все о Пифагоре? (Полина и Катя – они работают над проектом по этой теме). Вот они и будут нашими пилотами. Попросим их подойти к штурвалу. У нас все готово к полету. Теперь в путь!
Полина. Мы рады всех приветствовать на борту нашего самолета. И пока мы набираем скорость, давайте вспомним формулировку главной теоремы сегодняшнего путешествия – теоремы Пифагора. (В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.) Совершенно верно. Мы надеемся, что сегодняшнее путешествие позволит вам убедится еще и в том, что эта теорема – одна из главных теорем, которые применяются в нашей жизни.
Катя. А девизом для нашего путешествия мы выбрали слова:
Суть истины вся в том, что нам она – навечно,
Когда хоть раз в прозрении ее увидим свет,
И теорема Пифагора через столько лет
Для нас, как для него, бесспорна, безупречна.
- Как вы думаете, почему мы взяли именно это стихотворение? (Возможно потому, что мы рассмотрим применение теоремы Пифагора в его эпоху и в наше время.)
- Совершенно верно.
Полина. И вот мы с вами уже прилетели в Древний Вавилон. (Звучит музыка. Слайд)
Задача из самых ранних вавилонских текстов.
Палка длиной 1/2, прислонена к стене. Ее верхний конец опустили на 1/10. Как далеко отодвинется ее нижний конец?
Решение. Переведем условие задачи на язык геометрии. По данным: гипотенузе  и одному из катетов
и одному из катетов  необходимо найти второй катет. Его, как и
необходимо найти второй катет. Его, как и 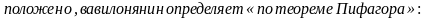
 3/10.
3/10.
Ответ:  .
.
Катя. Мы продолжаем путешествие сейчас мы отправимся в загадочную Индию. (звучит музыка. Слайд)
Древнеиндийская задача.
Над озером тихим
 С полфута размером
С полфута размером
Высился лотоса цвет.
Он рос одиноко,
И ветер порывом
Отнес его в сторону. Нет
Боле цветка над водой.
Нашел же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
«Как озера вода здесь глубока?»
По задаче составим чертеж.
Решение. Пусть глубина озера  , тогда
, тогда  Из
Из  по теореме Пифагора имеем
по теореме Пифагора имеем  ,
,
 ,
,
 ,
,
 .
.
Таким образом, глубина озера составляет 3,75 фута.  .
.
Ответ: 3,75 фута или 1,125 м.
Побудем еще в Индии и рассмотрим современные задачи (интерактивные слайды) (решение у доски и в тетрадях)
Стебель камыша выступает из воды озера на 1 м. Его верхний конец отклонили от вертикального положения на 2 м, и он оказался на уровне воды. Найдите глубину озера в месте, где растет камыш.
 Ответ 1,5
Ответ 1,5
Используя данные, приведенные на рисунке, найдите расстояние в метрах между пунктами A и B, расположенными на разных берегах озера.
 Ответ:500.
Ответ:500.
Полина. А сейчас нас встречает солнечный Китай.
Задача о бамбуке из древнекитайского трактата
 «Гоу-гу».
«Гоу-гу».
Имеется бамбук высотой в 1 чжан. Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня ( 1 чжан = 10 чи). Какова высота бамбука после сгибания?
Решение. Пусть высота бамбука после сгибания равна х. По теореме Пифагора
 ,
,
 ,
,
 ,
,
 =5,45 чи.
=5,45 чи.
Ответ: 5,45 чи.
Катя. Как мы видим, что задачи на теорему Пифагора встречаются у разных народов. И все они решаются по одному алгоритму. Давайте все вместе попробуем его сформулировать.
Алгоритм решения задач по теореме Пифагора:
Внимательно прочти задачу, разберись с условием.
По условию сделай чертеж.
Выдели в чертеже прямоугольный треугольник.
Найди катеты и гипотенузу.
Запиши теорему Пифагора и соотнеси данные в задаче с ней.
Выполни подстановку данных.
Соотнеси полученный ответ с вопросом задачи и смыслом условия.
Для того, чтобы вы лучше могли усвоить материал по данной теме, мы разработали Сборник задач «Теорема Пифагора в задачах реальной математики». Кроме этого, мы «В контакте» создали группу «Последователи Пифагора», с помощью которой мы надеемся привлечь молодежь к науке, в частности к математике, мы приглашаем всех присутствующих присоединиться к нашей группе, можете найти там интересные материалы о Пифагоре и его теореме, а так же разместить при желании свои. И, конечно же, мы хотели, чтобы вы написали ваши отзывы о нашем сборнике.
Полина. Ну а сейчас мы продолжим наше путешествие, и я предлагаю вернуться в Россию в 17 век.
Задача из учебника «Арифметика» Леонтия Магницкого.
Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать.
Решение. По теореме Пифагора
 ,
,
 ,
,
 стоп.
стоп.
Ответ: 44 стоп.
«Умение решать задачи – такое же практическое искусство. Ему можно научиться только путем подражания или упражнения» - говорил Пойа.
Поэтому сейчас, как вы уже догадались, мы будем решать задачи. Мы рассмотрим уже современные задания, взятые их КИМов ОГЭ.
Задача. Пожарную лестницу длиной 13 м приставили к окну пятого этажа дома. Нижний конец лестницы отстоит от стены на 5 м. На какой высоте расположено окно? Ответ дайте в метрах.
Решение.
Задача сводится к нахождению катета прямоугольного треугольника:
 = 12
= 12


Ответ: 12.
Задача. Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Решение.
Задача сводится к нахождению катета прямоугольного треугольника, по теореме Пифагора он равен:
2,4
Ответ: 2,4.
Задача. Длина стремянки в сложенном виде равна 1,85 м, а её высота в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах) между основаниями стремянки в разложенном виде.
Задание 17 № 311962. (из интернета)
Задание 17 № 311962. Лестница соединяет точки A и B и состоит из 35 ступеней. Высота каждой ступени равна 14 см, а длина — 48 см. Найдите расстояние между точками A и B (в метрах).
Решение.
Высота и длина каждой ступени составляют катеты прямоугольного треугольника, найдём гипотенузу этого треугольника по теореме Пифагора:
 = 50 см.
= 50 см.
Всего ступеней 35, следовательно, расстояние между точками A и B равно 50 · 35 = 1750 см = 17,5 м.
Ответ: 17,5.
А сейчас мы с вами отправимся погулять. Путь жука.
У дороги лежит тесаный гранитный камень в 30см длины, 20 см высоты и такой же толщины. В точке А – жук, намеривающийся кратчайшим путем направиться к углу В. Как пролегает этот кратчайший путь и какой он длины?
Решение. Кратчайший путь легко определится, если мы мысленно повернем верхнюю грань камня так, чтобы она оказалась в одной плоскости с передней.
Тогда АВ – кратчайший путь. АВ=50 см.
Ответ: 50 см.
Задача. Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии от дома оказался мальчик?
Решение.
Мальчик идёт вдоль сторон прямоугольного треугольника поэтому, искомое расстояние можно найти по теореме Пифагора:

Ответ: 1000.
Задача. Мальчик и девочка, расставшись на перекрестке, пошли по взаимно перпендикулярным дорогам, мальчик со скоростью 4 км/ч, девочка 3 км/ч. Какое расстояние (в км) будет между ними через 30 мин?
Ответ: 2,5
Диагностическая работа
Вариант 2,, стр. 17
Проверка результатов с помощью системы тестирования ActivExpression.
Учитель: Итак, мы сегодня решали с вами задачи на применение теоремы Пифагора, и прежде чем завершить наше путешествие, я хотела бы еще раз подчеркнуть, что несмотря на предельную простоту, Теорема Пифагора, по мнению многих математиков, относится к разряду наиболее выдающихся математических теорем за всю историю математики. Да и личность самого Пифагора неординарная. В историю он вошел не только как математик, а как философ, общественный деятель, учитель. И нам, потомкам, он оставил много заповедей. Некоторые из них перед вами на экране. Я предлагаю, каждой группе выбрать высказывание, которое, по вашему мнению, подходит к нашему занятию.
Заповеди Пифагора
Не делай ничего постыдного ни в присутствии других, ни втайне. Первым твоим законом должно быть уважение к себе самому.
Не закрывай глаз, когда хочешь спать, не разобравши всех своих поступков за прошедший день.
Будь другом истины до мученичества, но не будь ее защитником до нетерпимости.
Полезнее наобум бросить камень, чем пустое слово.
Прежде всего не теряй самоуважения!
Все исследуй, давай разуму первое место.
Делай великое, не обещая великого.
Для познания нравов какого ни есть народа старайся прежде изучить его язык.
Если можешь быть орлом, не стремись стать первым среди галок.
Жизнь подобна игрищам: иные приходят на них состязаться, иные — торговать, а самые счастливые — смотреть.
Избери себе друга; ты не можешь быть счастлив один: счастье есть дело двоих.
Как ни коротки слова «да» и «нет», все же они требуют самого серьезного размышления.
Молчи или говори что-нибудь получше молчания.
Делай лишь то, что впоследствии не огорчит тебя и не принудит раскаиваться.
Помогай не тому, кто ношу сваливает, а тому, кто её взваливает.
(выступление учащихся). Я с вами абсолютно согласна, ребята. Как мы видим, что все заповеди Пифагора актуальны и сегодня.
Ученик: Видел в математике он свет,
Как художник, как большой поэт.
Числам придавал огромный вес,
Он считал их чудом из чудес.
И в своих работах отмечал:
Числа - есть начало из начал.
Гениальным проникал умом
Сущность теорем и аксиом.
Многие его ученики
В мир несли культуры огоньки.
Не случайно с нами до сих пор
Мудрый, легендарный Пифагор!
Пребудет вечная истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
В исполнении учащихся звучит гимн Математике.
Заключительное слово учителя:
А знаете ли вы, что Парижской академией наук была даже установлена премия в 100.000 франков тому, кто первый установит связь с обитателем другой планеты?
Эта премия все еще ждет счастливца. Было решено передать обитателям Марса сигнал в виде теоремы Пифагора.
Может эта премия ждет именно вас? Дерзайте!
Спасибо за занятие.





 МБОУ «Золотухинская средняя
МБОУ «Золотухинская средняя 

 и одному из катетов
и одному из катетов  необходимо найти второй катет. Его, как и
необходимо найти второй катет. Его, как и 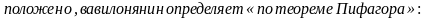
 3/10.
3/10. .
. С полфута размером
С полфута размером , тогда
, тогда  Из
Из  по теореме Пифагора имеем
по теореме Пифагора имеем  ,
, ,
, ,
, .
. .
. Ответ 1,5
Ответ 1,5 Ответ:500.
Ответ:500. «Гоу-гу».
«Гоу-гу». ,
, ,
, ,
,









