Сценарий занятия по математике на тему «Понятие комплексного числа. Действия с комплексными числами»
Преподаватель математики Пересыпкина Елена Алексеевна,
ГОБПОУ «Липецкий машиностроительный колледж»
Тип урока: ОНЗ
Тема «Понятие комплексного числа. Действия с комплексными числами»
Основные цели:
Метапредметные:
1) Тренировать владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания.
2) Тренировать умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность.
3) Тренировать умение продуктивно общаться и взаимодействовать в процессе совместной деятельности.
Предметные:
Сформировать понятие комплексного числа.
Сформировать умение выполнять действия с комплексными числами
Тренировать умение выполнять действия с действительными числами. Сформировать навыки решения уравнений с отрицательным дискриминантом.
Оборудование
1) Демонстрационный материал:
2) Раздаточный материал.
Ход урока
Мотивация к учебной деятельности
УУД, формирующиеся на данном этапе:
Регулятивные: волевая саморегуляция.
Личностные: действие смыслообразования
Коммуникативные: планирование учебного сотрудничества с учителем и со сверстниками.
− Добрый день, ребята!
– Какую тему вы повторяли на предыдущих уроках? (Действия с действительными числами, решение квадратных уравнений)
–Кто-нибудь из вас задумывался, существуют ли числа, не принадлежащие множеству действительных чисел? Можете ли вы представить, какие это числа, какими свойствами обладают? Сегодня мы будем размышлять над этим вопросом.
– Прочитайте, пожалуйста, высказывание известного советского математика Наума Яковлевича Виленкина «Решение трудной математической проблемы можно сравнить с взятием крепости»
– Как вы понимаете эти слова? (Как взятие труднодоступной крепости требует терпения, упорства, владения тактикой и стратегией -так и решение трудной математической проблемы невозможно без знания основных математических понятий, методов, приемов и твердости в достижении цели)
– Сегодня при изучении нового материала вы будете продолжать расширять свои знания о множествах чисел и действиях с числами.
2. Актуализация знаний и фиксация затруднения в пробном учебном действии.
УУД, формирующиеся на данном этапе:
Познавательные:
общеучебные: умение структурировать знания, контроль и оценка процесса и результатов деятельности;
логические: анализ, синтез, выбор оснований для сравнения.
Регулятивные: контроль - в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;
коррекция — внесение необходимых дополнений и корректив.
–Выполняется взаимная проверка выполненных домашних работ учащимися и повторение основных свойств сложения , вычитания, умножения, деления и сравнения действительных чисел, решения квадратных уравнений
| Пример 1. Вычислите  . . Решение:  . . Ответ: 2,8.
|
| Пример 2. Проверить справедливость равенства.  Решение. Рассмотрим равенство  . Очевидно, что если оно верно, то верно и заданное равенство. Пусть . Очевидно, что если оно верно, то верно и заданное равенство. Пусть Проанализировав выражения, получим, что a 0, b 0. Если при этом выполняется равенствоa2 = b2, то a = b. Находим Проанализировав выражения, получим, что a 0, b 0. Если при этом выполняется равенствоa2 = b2, то a = b. Находим  Так как a2 = b2, то a = b, т.е. заданное равенство справедливо. |
| Пример 3 Решить уравнение 
|
− Проверьте правильность выполнения, воспроизведите понятия, которые использовали. Если при выполнении задания у кого-то возникли затруднения, ошибки необходимо исправить, на работу 3 минуты.
− Что вы сейчас повторили по теме «Действительные числа. Действия с действительными числами»? (Основные свойства сложения , вычитания, умножения, деления и сравнения действительных чисел, свойства арифметического квадратного корня из положительного числа).
-Вы знаете определение арифметического квадратного корня из положительного числа. А также вам известно, что квадратный корень из отрицательного числа не существует, т.к. нет такого действительного числа , которое при возведении в квадрат равно отрицательному числу.
–Подготовку к открытию начнете с выполнения следующего задания
Решите уравнение
а) x2-49=0; б) 9x2-4=0; в) 64x+4x2=0;
Решение:
а) x2=49, отсюда x=±7. Ответ: -7; 7
б)
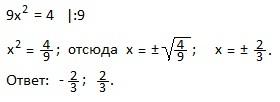
в) 64x+4x2=0. Вынесем общий множитель 4х за скобки:
4х(16+х)=0. У нас три множителя, 4≠0, следовательно, или х=0 или 16+х=0. Из последнего равенства получим х=-16.
Ответ: -16; 0.
– Что повторили? (Для выполнения задания использовали определения арифметического квадратного корня, действия с действительными числами)
– Задание на пробное действие:
Решите уравнение x2+1=0
Учащиеся самостоятельно пытаются выполнить задание. Время на выполнение задания ограничено.
3. Выявление места и причины затруднения
УУД, формирующиеся на данном этапе:
Познавательные:
общеучебные:умение структурировать знания;
постановка и формулирование проблемы;
умение осознанно и произвольно строить речевое высказывание
логические ; анализ объектов с целью выделения признаков
-Ответьте на вопросы:
1) какое задание должны были выполнить;
2) в каком месте и почему возникло затруднение?
Возможные варианты ответов:
– Необходимо было назвать число, квадрат которого равен отрицательному числу. Затруднение возникло в том, что в множестве действительных чисел извлекать корень квадратный из отрицательного числа нельзя. Причина в том, что мы пока не знаем какое число после возведения в квадрат равно отрицательному числу.
4. Построение проекта выхода из затруднения
УУД, формирующиеся на данном этапе:
Регулятивные: целеполагание, как постановка учебной задачи,
планирование, прогнозирование.
Познавательные:
общеучебные : постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности
выбор наиболее эффективных способов решения задач в зависимости от конкретных условий
− Подумайте и сформулируйте цель дальнейшей деятельности;
Возможный вариант ответа:
Цель: Узнать, как извлечь корень квадратный из отрицательного числа, и какое число после возведения в четную степень равно отрицательному числу.
– Составьте план ваших действий.
Возможный вариант ответа:
1. Выполнить задания, предложенные учителем, проанализировать результаты.
2. Сформулировать выводы.
3. Сравнить с эталоном.
5. Реализация построенного проекта
УУД, формирующиеся на данном этапе:
Коммуникативные:планирование учебного сотрудничества со сверстниками, инициативное сотрудничество в поиске и сборе информации; умение выражать свои мысли.
Познавательные:
общеучебные: поиск и выделение необходимой информации, применение методов информационного поиска; смысловое чтение и выбор чтения в зависимости от цели; умение осознанно и произвольно строить речевое высказывание;
логические: построение логической цепи рассуждений, анализ, синтез.
постановки и решения проблем: самостоятельное создание способов решения проблем поискового характера.
– Выполните следующие задания.
Вычислите:
а)  ; б)
; б) ;
;
Возможный вариант ответа:
1.По свойству корней  =
= ·
·
а)  =
= =
= ·
· =3·
=3·
б)  =
= =
= =4·
=4·
2.Но корня квадратного из (-1) на множестве действительных чисел не существует. Может быть, надо ввести новое число?
-Ребята, как бы вы назвали новое число?
Возможный вариант ответа:
1)Несуществующая единица,
2) Невозможное число,
3) Число, которое равно 
| Определение. Мнимая единица-это число, квадрат которого равен -1. Обозначается буквой i. i =-1 =-1 i= |
– Выполните с помощью нового эталона задание на пробное действие.
а )  =
= =
= ·
· =3·
=3· =3i
=3i
б)  =
= =
= =4·
=4· =4i.
=4i.
– Удалось преодолеть затруднение?
– Важно, что при таком определении, сохраняются все основные свойства действий с действительными числами. А понятие мнимой единицы можно расширить до определения комплексного числа
| Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i –мнимая единица. Число  называется действительной частью числа называется действительной частью числа  : :  , а число , а число  - его мнимой частью: - его мнимой частью:  . . Два комплексных числа  и  у которых действительные части равны, а коэффициенты при мнимой части — противоположные числа, называются комплексно-сопряженными.
Для комплексных чисел понятия равенства и операции сложения и умножения вводятся следующим образом: Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда Суммой двух комплексных чисел a + ib и c + id называется комплексное число Произведением двух комплексных чисел a + ib и c + id называется комплексное число | ac – bd + i(ad + bc). | |
| | 4.Деление комплексных чисел. Для комплексных чисел, записанных в алгебраической форме:  и и 
|
|
6. Первичное закрепление во внешней речи
УУД, формирующиеся на данном этапе:
Коммуникативные: управление поведением партнера;
умение выражать свои мысли.
Регулятивные: контроль - в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;
коррекция — внесение необходимых дополнений и коррективов в план и способ действия
оценка — выделение и осознание обучающимся того, что уже усвоено и что ещё нужно усвоить, осознание качества и уровня усвоения;
Познавательные:
общеучебные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий
рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности
– Выполните задания
Даны два комплексных числа Z1= (7 + 2i ) и Z2=(3 – 4i ). Найдите их сумму, разность, произведение и частное
Учащиеся выполняют задания под руководством учителя, обращая внимание на применение новых определений и свойств.
Пример: (5+3i)+(3−i)=8+2i(5+3i)+(3−i)=8+2i
Пример: . (5+3i)−(3−i)=2+4i(5+3i)−(3−i)=2+4i
Пример: (3+2i)⋅(4−i)=12−3i+8i−2i2=14+5i(3+2i)⋅(4−i)=12−3i+8i−2i2=14+5i
Пример: Решить уравнение  .
.
Решение. Дискриминант данного уравнения:  меньше нуля, но теперь мы можем воспользоваться мнимой единицей:
меньше нуля, но теперь мы можем воспользоваться мнимой единицей:
 , т.е.
, т.е.  ;
;  .
.
Пример
– Выполните задания в парах.
Задание выполняется в парах, по вариантам. Проверка проводится по подробному образцу
| Вариант 1. 1. Даны два комплексных числа Z1= (10 + 2i ) и Z2=(1 – 6i ). Найдите их сумму, разность, произведение и частное. 2. Проверьте правильность следующих утверждений: а) Сумма и разность чисто мнимых чисел есть чисто мнимое число. Для проверки возьмите числа: Z1=2i, Z2=-3i б) Произведение двух чисто мнимых чисел равно действительному числу. Для проверки возьмите числа: Z1=-5i, Z2=3i в) Квадрат чисто мнимого числа равен действительному отрицательному числу. Для проверки возьмите числа: Z1=10i г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу. Для проверки возьмите числа: Z1=7i, Z2=3
Вариант 2. 1.Даны два комплексных числа z1= (12 + 2i ) и z2=(3 – 4i ). Найдите их сумму, разность, произведение и частное. 2. Проверьте правильность следующих утверждений: а) Сумма и разность чисто мнимых чисел есть чисто мнимое число. Для проверки возьмите числа: Z1=2i, Z2=-3i б) Произведение двух чисто мнимых чисел равно действительному числу. Для проверки возьмите числа: Z1=-5i, Z2=3i в) Квадрат чисто мнимого числа равен действительному отрицательному числу. Для проверки возьмите числа: Z1=10i г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу. Для проверки возьмите числа: Z1=7i, Z2=3
|
Ответы:
| Вариант 1 1. Z1+ Z2=11 – 4i 2. Z1- Z2=9 +8i 3. Z1 Z2=22 -58i 4. 
| Вариант 2 1. Z1+ Z2=15 – 2i 2. Z1- Z2=9 +6i 3. Z1 Z2=44 -42i 4.  |
После самопроверки проводится рефлексия: выясняется, есть ли ошибки, если есть, то проговаривается, как надо было выполнить задание.
7. Самостоятельная работа с самопроверкой по эталону
УУД, формирующиеся на данном этапе:
Регулятивные: контроль - в форме сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;
коррекция — внесение необходимых дополнений и коррективов в план и способ действия
оценка — выделение и осознание обучающимся того, что уже усвоено и что ещё нужно усвоить, осознание качества и уровня усвоения; оценка результатов работы
Познавательные:
общеучебные: умение осознанно и произвольно строить речевое высказывание
выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
контроль и оценка процесса и результатов деятельности
− Что дальше необходимо сделать?
− С какой целью вы будете выполнять самостоятельную работу?
Для самостоятельной работы учащимся предлагается выполнить следующие задания
Вариант 1
Задание 1. Выполните все действия(сложение, вычитание, умножение, деление) с комплексными числами:
 ;
; 
Задание 2. Решите уравнение:
 ;
;
Вариант 2
Задание 1. Выполните все действия(сложение, вычитание, умножение, деление) с комплексными числами:
 ;
;
Задание 2. Решите уравнение:
 ;
;
Вариант 3
Задание 1. Выполните все действия(сложение, вычитание, умножение, деление) с комплексными числами:
 ;
;
Задание 2. Решите уравнение:

Вариант 4
Задание 1. Выполните все действия(сложение, вычитание, умножение, деление) с комплексными числами:
 ;2+4i
;2+4i
Задание 2. Решите уравнение:
 ;
;
Учащиеся выполняют самостоятельную работу и проводят самопроверку по эталону для самопроверки
| Подробный образец | Эталон |
| (5+3i)+(3−i)=8+2i(5+3i)+(3−i)=8+2i
| Свойство сложения: Сумма двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i=(a+c)+(b+d)i
|
| . (5+3i)−(3−i)=2+4i(5+3i)−(3−i)=2+4i
| Свойство вычитания: Разность двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1−z2=(a+bi)−(c+di)=(a−c)+(b−d)i
|
| (3+2i)⋅(4−i)=12−3i+8i−2i2=14+5i(3+2i)⋅(4−i)=12−3i+8i−2i2=14+5i | Свойство умножения: Произведением двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1⋅z2=(a+bi)⋅(c+di)=(ac−bd)+(ad+bc)i
|
| Решить уравнение  . . Решение. Дискриминант данного уравнения:  меньше нуля, но теперь мы можем воспользоваться мнимой единицей: меньше нуля, но теперь мы можем воспользоваться мнимой единицей:  , т.е. , т.е.  ; ;  . .
| Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a не равно 0. Для решения квадратного уравнения можно использовать формулы:
и
|
− Проанализируйте результаты выполнения самостоятельной работы: назовите, в каких местах и почему возникли затруднения.
8. Включение в систему знаний и повторение.
УУД, формирующиеся на данном этапе:
Регулятивные: прогнозирование- предвосхищение результата и уровня усвоения знаний
Познавательные:
общеучебные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
контроль и оценка процесса и результатов деятельности
заданиях1-2 учащиеся формируют умение применять определение и свойства комплексных чисел при выполнении различных арифметических действий
1.Даны комплексные числа  ,
,  .Найти частное
.Найти частное 
2. Дано комплексное число  . Записать данное число в алгебраической форме (т.е. в форме
. Записать данное число в алгебраической форме (т.е. в форме  ).
).
В заданиях 3-4 учащиеся тренируют умение решать квадратные уравнения с отрицательным дискриминантом и уравнения с комплексным коэффициентами.
Решение:
3. Решить квадратное уравнение 
Вычислим дискриминант:

Дискриминант отрицателен, и 
По известным формулам получаем два корня:

 – сопряженные комплексные корни
– сопряженные комплексные корни
Таким образом, уравнение  имеет два сопряженных комплексных корня:
имеет два сопряженных комплексных корня:  ,
, 
4. Решить уравнения:
а) х2 + (5 – 2i) x + 5(1– i) = 0;
б) х2 + (1 – 2i) х – 2i = 0;
9. Рефлексия деятельности на уроке
УУД, формирующиеся на данном этапе:
Познавательные:
общеучебные: умение структурировать знания;
оценка процесса и результатов деятельности
Коммуникативные: умение выражать свои мысли.
Регулятивные: волевая саморегуляция; оценка – выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению.
-Ребята, как вы думаете, что имел в виду испанский физик, исследователь Хорхе Вагенсберг, говоря что «Комплексные числа помогают из-за обратной стороны зеркала справиться с недостатками вещественных чисел»?
− А теперь каждый проанализируйте свою работу.
Учащиеся заполняют индивидуальные карточки :
| Понятия и способы действий | Знаю | Получилось применить |
| Определение мнимой единицы, комплексного числа. |
|
|
| Свойства действий с комплексными числами. |
|
|
| Решение уравнений с отрицательным дискриминантом |
|
|
Домашнее задание
| П. 5,7 (повторить эталоны) |