Технол. карта. Геометрия для 9 кл "Сумма векторов"

1

Ф И О

Короткова Ольга Викторовна

2

Предмет

геометрия

3

Класс

9

4

Тема урока

Сумма векторов

5

Базовый учебник

Атанасян Л.С. Геометрия ,7-9:

учебник для общеобразовательных учреждений. М. Просвещение, 2013 г.

№

п/п

Этапы урока

Цели и задачи этапа

1

Организационный момент.

Определить цель занятия.

Подготовка учащихся к работе на занятии, быстрое включение учащихся в деловой ритм.

2

Актуализация знаний и умений учащихся (теоретический опрос).

Выявить уровень усвоения теоретического материала.

Привитие навыков самоконтроля для коррекции пробелов.

3

Учебно-познавательная деятельность.

Научить строить сумму двух векторов, используя правило треугольника и правило параллелограмма.

Составление опорного конспекта.

Умение структурировать знания.

4

Закрепление изученного материала.

Совершенствовать навыки решения задач.

Строить логическое рассуждение при решении задачи.

5

Подведение итогов урока.

Домашнее задание.

Рефлексия.

Оценить результаты собственной работы на уроке.

Самостоятельность в закреплении учебных навыков, полученных на уроке. Расширение кругозора по теме.

Дать оценку собственной работе.

№

п/п

Деятельность учителя

Деятельность ученика

1

Организационный момент.

Учитель приветствует учащихся.

Подготовка учащихся к работе на занятии, быстрое включение учащихся в деловой ритм.

2

Актуализация знаний и умений учащихся .

Слайд №2.

1.Как называются величины, которые имеют не только числовые значения, но и направление в пространстве?

2.Длина вектора.

3.Равные векторы.

4. Какой вектор называется нулевым?

5. Дайте определение коллинеарных векторов.

6. Назовите векторные величины: масса, температура, длина, площадь, сила, скорость, длина.

2) Слайд №3.

ABCD – параллелограмм.

B C

A D

По данному рисунку назовите :

• Векторы, изображенные на рисунке.

• Противоположно направленные векторы .

• Равные векторы.

• Векторы одинаковой длины.

• Сонаправленные векторы.

• Коллинеарные векторы.

Учащиеся устно отвечают на вопросы, решают задачи.

-Вектор - направленный отрезок.

- Длина вектора - это длина отрезка его задающего.

- Векторы называются равными, если они сонаправлены и их длины равны.

- Нулевой вектор-это вектор, у которого начало и конец совпадают.

- Векторы называются коллинеарными, если лежат на одной прямой или на параллельных прямых.

- Сила, скорость.

По рисунку отвечают на вопросы.

3

Учебно-познавательная деятельность .

Слайд №4

Ввести понятие суммы двух векторов

(правило треугольника).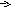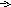

b В b С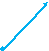

а

a

a+ b

А

→

Вектор АС называется суммой векторов а и b.

Даны два вектора  и . Отметим произвольную точку A и отложим от этой точки вектор , равный вектору . Затем от точки B отложим вектор , равный вектору . Вектор  называется суммой векторов   и .

Это правило называется «правило треугольника».

Слайд № 5 Сумма вектора а и нулевого вектора

Слайд № 6

1. Применить правило треугольника для нахождения суммы коллинеарных векторов.

→ →

А) Векторы а и b сонаправлены.

а b

A a B b C m

A a + b С

→ →

Слайд № 7 Б) Векторы а и b противоположно направлены.

а b

A a B m

С b

a + b = АС

Слайд № 8

Сложение векторов по правилу параллелограмма.

b

B C

a

A

D

Рассмотрим те же два вектора  и . От произвольной точки А отложим вектор , равный вектору  и затем вектор , равный вектору . Построим параллелограмм АВСD, проведем в нем диагональ AC тогда вектор  равен сумме векторов  и . Этот прием построения суммы векторов называется «правилом параллелограмма».

Слайд № 9. Нахождение суммы векторов по правилу треугольника и параллелограмма.

Есть ли разница в том, каким правилом вы пользуетесь при нахождении суммы векторов?

А) Правило треугольника. Б) Правило параллелограмма

b b В С

В С

a a

a a+ b

a+b

А А b D

Слайд № 10

1. Законы сложения векторов:

А) переместительный закон a + b = b + a.

Б) Сочетательный закон: (a + b) + c = a+ (b + c).

Научить строить сумму векторов, используя правило треугольника и правило параллелограмма..

Учащиеся выполняют аналогичные построения в тетради, составляют опорный конспект.

Если А, В, С произвольные точки, то

→ → →

АВ +ВС = АС (правило треугольника).

Записать в тетради

→ → →

а + 0 = а

Учащиеся выполняют аналогичные построения в тетради.

Учащиеся выполняют аналогичные построения и записи в тетради.

Учащиеся выполняют аналогичные построения и записи в тетради.

→ → →

АВ +ВС = АС

Применение – физика (сложение двух сил).

→ → →

Вектор АС - сумма векторов а и b.

Результаты получаются одинаковые, независимо от того каким правилом воспользоваться.

Проговаривают законы сложения векторов и записывают в тетрадь.

4

Закрепление изученного материала

Cлайд № 11- 14.

Найдите сумму векторов (устно).

В С В С В С C

В C

А D А D А D

Слайд № 15

Задача № 115 в печатной рабочей тетради:

Используя правило треугольника, найди сумму векторов:

а) ; б) ; в) ; г) .

Задача № 759(а), решить без помощи чертежа.

|

Слайд № 16

Задача № 762.

а) В б) В D

а а а O

А а С

А а С

Отвечают устно, объясняют, какое правило применяли.

→ → →

АВ, АС, АС

Решение проверяется в презентации

Слайд № 15):

а)   
б)
в) AD + 0 = AD + DD= AD
г)

Задача № 759(а).

→ → → →

Доказать, что МN + NQ = MP + PQ

Доказательство:

→ → → → → →

MN + NQ =MQ , MP + PQ = MQ ,

→ →

MQ = MQ - равенство верно.

Задача № 762.

Решение .

→ → →

а) | АВ + ВС| = |АС| = а,

→ → → →

б) |АВ + АС | = |AD| = |2AO| = 2√a² - a²̸ 4 =

=a √3

5

Итоги урока. Рефлексия. (2 мин.)

- Какие правила для построения суммы векторов изучили на уроке?

- В чем их отличие?

- Оцените свою работу на уроке.

- Выставление оценок за работу.

Домашнее задание (учитель комментирует задание).

Слайд № 17 , 18

Учащиеся записывают домашнее задание:

П. 79, 80, № 753, 759 (б), 763 (б, в).