МОАУ "Лицей №1"
Разработка урока алгебры в 7 классе
по теме:
«Графический способ решения
систем линейных уравнений с двумя переменными».
Учитель математики
Ахметзянова Айнара Тюлегеновна
2017-2018 уч.год
Предмет: алгебра
Учебный план: 3 часов в неделю
Класс: 7Б
Тема: Графический способ решения систем линейных уравнений с двумя переменными.
| Цели деятельности учителя | Главная дидактическая цель: формировать представления о многообразии действий с отрицательными числами. Формировать УУД: Личностные: умение ясно, точно, грамотно излагать свои мысли; умение осуществлять самооценку на основе критерия успешности учебной деятельности; проявление положительного отношения к урокам математики, интереса к учебному материалу, способам решения новых учебных задач; доброжелательное отношение к сверстникам. Регулятивные: уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; принимать и сохранять учебную задачу; работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной оценки; планировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе оценки и учета характера сделанных ошибок, высказывать свое мнение. Коммуникативные: умения оформлять свои мысли в устной форме; слушать и понимать речь других, совместно договариваться о правилах поведения и общения в школе и следовать им; выражать свои мысли с достаточной полнотой и точностью; допускать возможность существования у людей различных точек зрения. Познавательные: умения ориентироваться в своей системе знаний (отличать новое от уже известного с помощью учителя), добывать новые знания (находить ответы на вопросы, используя учебник, свой жизненный опыт, информацию, полученную на уроке); осуществлять выбор наиболее эффективных способов решения в зависимости от конкретных условий; структурировать знания; использовать знаково-символические средства.
|
Тип урока: урок изучения нового материала.
Задачи: создать условия для развития умений формулировать определение решения системы линейных уравнений с двумя переменными, описывать графический метод решения системы двух линейных уравнений с двумя переменными, определять количество решений системы двух линейных уравнений с двумя переменными, решать графически систему уравнений
| Планируемые результаты |
| Предметные: освоят основные понятия о решении систем уравнений; научатся правильно употреблять термины; уравнение с двумя переменны и, система, станут понимать их в тексте, в речи учителя | Метапредметные: познавательные- осуществлять сравнение, сериацию и классификацию, самостоятельно выбирая основания и критерии для указанных логических операций; строить классификацию путем дихотомического деления; регулятивные- работать по самостоятельно составленному плану, сверяясь с ним и с целью деятельности, исправляя ошибки, используя самостоятельно подобранные средства; коммуникативные- уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций | Личностные: формировать умение планировать свои действия в соответствии с учебным заданием |
Учебник Алгебра 7 класс, автор: Ю. Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова
| Этапы урока и их содержание | Время | Деятельность |
| Учителя | Ученика |
| 1.Организационный этап. | 1 мин | Здравствуйте ребята! Садитесь! Я вижу все готовы к уроку! Начнем нашу работу. | Слушают учителя |
| 2.Мотивация к учебной деятельности. ЦЕЛИ: актуализировать требования к ученикам с позиций учебной деятельности; создать условия для формирования внутренней потребности во включении в учебную деятельность; установить тематические рамки и наметить шаги учебной деятельности | 5 мин | Устная разминка! 1. Является ли пара чисел (2;-5) решением уравнения: А) 2х+у=9; Б) х-у=7; В) -х+у=3; Г) у-2х=-9? Что такое линейное уравнение? Сколько решений имеет линейное уравнение с двумя переменными? Выразите переменную у через х из уравнения х+у=1; 3х-у=2. Какую тему мы начали проходить на прошлом уроке? Что же такое система уравнений? А сколько может быть уравнений в системе? Что значит решить систему уравнений? Что является решением системы уравнений? | Отвечают на вопросы учителя. Делают проверку устно 1. А) не подходит Б) подходит В)не подходит Г)подходит 2. А) подходит Б)не подходит во второе В)не подходит во второе. у=1-х -у=2-3х у=3х-2
|
| 3.Актуализация и фиксирование индивидуального затруднения, выявление места и причины затруднения. ЦЕЛИ: создать условия для выполнения учащимися пробного учебного действия; выявить шаг (место, операцию) затруднения и зафиксировать во внешней речи его причину | 4 мин | Аналогичные задания вы выполняли в домашней работе, откройте тетради и давайте проверим вместе. Проверка домашнего задания: №1057 а)решение; б) решение №1058 а) не решение (-3;4), (-2;-6)не решение; (-4;3)решение б) не решение (-3;4), (-2;-6) решение; (-4;3) не решение №1060вг в) (3;2) г) (0;2) Скажите пожалуйста, в чем заключается суть графического метода. А сколько решений может иметь система уравнений и от чего это зависит,???? На этот вопрос мы с вами ответим чуть позже на уроке.
| Отвечают на вопросы. Примерные ответы учеников: Это два уравнения, которые находятся знаком Два, три, ... Найти все ее решения или доказать, что решений нет. Пара значений переменных, обращающая каждое уравнение системы в верное равенство.
|
| 3.Построение проекта выхода из затруднения. ЦЕЛИ: организовать постановку цели урока; создать условия для составления совместного плана действий; определить пути и средства достижения цели | 5 мин | -Итак, какую тему мы продолжаем изучать на сегодняшнем уроке? -Верно, тема нашего урока: «Графический метод решения систем уравнений». -Какую цель вы поставите перед собой? -Выяснить при каком условии система имеет решение? -Сколько может иметь система уравнений решений?
| Высказывают свои предположения. Графический метод решения систем уравнений
Определить при каком условии система имеет решение и отчего это зависит, сколько может быть решений?
|
| 4.Реализация построенного проекта. ЦЕЛИ: создать условия для выполнения учащимися пробного учебного действия; выявить место (шаг, операцию) затруднения и зафиксировать во внешней речи его причину | 7 мин
| Ребята, мы сейчас с вами, будем работать по группам:1 группа-1 ряд, 2 группа-2 ряд, 3 группа-3 ряд. Каждая из групп будет решать систему уравнений графическим методом, через 5 мин один человек от каждой группы сделает вывод. Прежде чем приступать к графическому методу решений системы, давайте с вами еще раз проговорим алгоритм нашей работы (переворачиваем карточку с номером 1) Алгоритм решения системы уравнений графическим способом 1. Выразить из каждого уравнения переменную у через х. 2. Построить график каждого уравнения 3. Найти общее решение этих уравнений. 4. Записать ответ. (переворачиваем карточку с номером 2) Карточка 1 Решить систему уравнений графическим способом, используя алгоритм. � ��� ��� Как расположены прямые на плоскости? Сколько общих точек? Сколько решений имеет система уравнений? Сделайте общий вывод. Карточка 2 Решить систему уравнений графическим способом, используя алгоритм.  Как расположены прямые на плоскости? Сколько общих точек? Сколько решений имеет система уравнений? Сделайте общий вывод. Карточка 3 Решить систему уравнений графическим способом, используя алгоритм.
 Как расположены прямые на плоскости? Сколько общих точек? Сколько решений имеет система уравнений? Сделайте общий вывод. (переворачиваем карточку с номером 3) | Прямые | Общие точки | Система имеет | О системе говорят | |  
| Одна общая точка | Одно решение | Имеет решение, совместная | |  
| Нет общих точек | Не имеет решений | несовместная | |  
| Много общих точек | Много решений | неопределенная |
(переворачиваем карточку с номером 4)  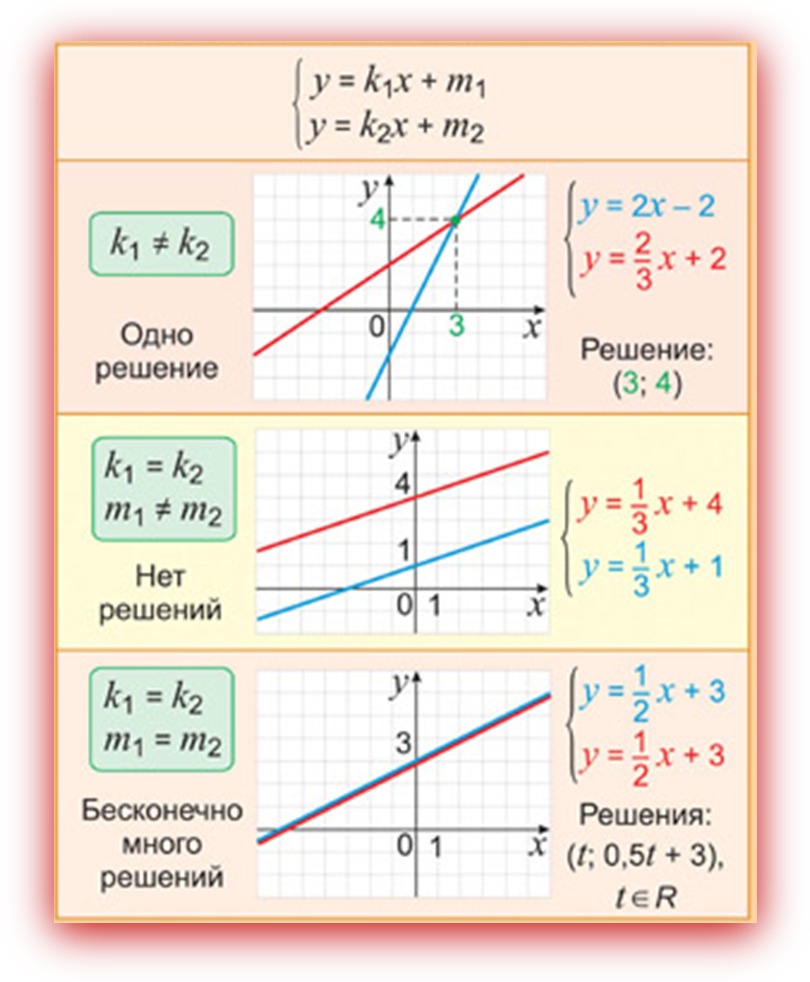 | Работают в тетрадях. Выполняют задания из карточки
(Ответ: 1 решение, (2,1)) 
(Ответ: прямые совпали, множество решений).  (Ответ: прямые параллельны, нет решений). 
|
|
|
| Физкультминутка Сколько решений имеет система уравнений?
1)  2) 2)  3) 3)  4) 5) 5)  6) 6)  7) 
|
|
| Закрепление умений и навыков. Цели: -закрепить новое знание в речи знаках; -зафиксировать преодоление возникшего затруднения. | 7 мин | - Выполним №1061а - 
№1062аг  
|  (0;-3)
единственное решение,
 Нет решений, -0,5=-0,5 |
|
| 5 мин | Задание №1063ав будем выполнять самостоятельно, затем обменяемся тетрадями в парах и проверим правильность выполнения задания друг у друга. Прежде чем приступить к выполнению задания, отчего зависит количество решений системы?
|
От коэффициента, стоящего перед переменной х.
,
 -единственное решение -единственное решение , коэффициенты одинаковые, графики совпадают, бесконечное множество решений |
| Рефлексия учебной деятельности. Цель: организовать рефлексию и оценку учениками собственной деятельности (самооценку) | 5 мин
2 мин | Оформление дерева знаний. Ребята , давайте еще раз вспомним: Что такое система линейных уравнений? Алгоритм графического решения системы уравнений? Сколько система из двух линейных уравнений может иметь решений? Отчего это зависит?
|
|
| Домашнее задание | 2 мин | (переворачиваем карточку с номером 5 1)теория на странице 207-208, выучить определения, ответить на вопросы после пункта. 2)Письменно выполнить номера из учебника: №1061б, 1062бвд, 1063б. 3) Дополнительное задание*: подберите, если возможно, такое значение k, при котором данная система имеет единственное решение, не имеет решений, имеет бесконечное множество решений. � �
|
|
Рефлексия







1) Выразить переменную у через х из каждого уравнения;
2) Построить график каждого уравнения;
3)Найти общее решение.




система имеет бесконечно много решений, система неопределенная

единственное решение системы, система совместная


система не имеет решений, система несовместная
Приложение.
Карточки с заданиями
1 пара.
Решить систему уравнений графическим способом, используя алгоритм.
Как расположены прямые на плоскости?
Сколько общих точек?
Сколько решений имеет система уравнений?
Сделайте общий вывод.
2 пара.
Решить систему уравнений графическим способом, используя алгоритм.

Как расположены прямые на плоскости?
Сколько общих точек?
Сколько решений имеет система уравнений?
Сделайте общий вывод.
3 пара.
Решить систему уравнений графическим способом, используя алгоритм.

Как расположены прямые на плоскости?
Сколько общих точек?
Сколько решений имеет система уравнений?
Сделайте общий вывод.
Алгоритм решения системы уравнений графическим способом
1. Выразить из каждого уравнения переменную у через х.
2. Построить график каждого уравнения
3. Найти общее решение этих уравнений.
5. Записать ответ.
Сделайте общий вывод.
| Прямые | Общие точки | Система имеет | О системе говорят |
|  
| Одна общая точка | Одно решение | Имеет решение, совместная |
|  
| Нет общих точек | Не имеет решений | несовместная |
|  
| Много общих точек | Много решений | неопределенная |

Домашнее задание
1)теория на странице 207-208, выучить определения, ответить на вопросы после пункта.
2)Письменно выполнить номера из учебника: №1061б, 1062бвд, 1063б.
3) Дополнительное задание*: подберите, если возможно, такое значение k, при котором данная система имеет единственное решение, не имеет решений, имеет бесконечное множество решений.
� � � � � �
15



















 5)
5) 












