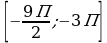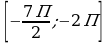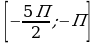1. ИНФОРМАЦИЯ О РАЗРАБОТЧИКЕ ПЛАНА
2. ОБЩАЯ ИНФОРМАЦИЯ ПО УРОКУ
| Класс: | 11 |
| Место урока (по тематическому планированию ПРП) | Решение тригонометрических уравнений |
| Тема урока: | Отбор корней в тригонометрических уравнениях на заданном отрезке графическом способом. |
| Уровень изучения: | углубленный |
| Тип урока: | урок освоения новых знаний и умений
|
| Планируемые результаты (по ПРП): |
| Личностные: уважения к прошлому и настоящему российской математики, ценностным отношением к достижениям российских математиков и российской математической школы. |
| Метапредметные: Базовые логические действия: выбирать способ решения учебной задачи. Базовые исследовательские действия: прогнозировать возможное развитие процесса, а также выдвигать предположения о его развитии в новых условиях. Универсальные коммуникативные действия: ясно, точно, грамотно выражать свою точку зрения в устных и письменных текстах, давать пояснения по ходу решения задачи, комментировать полученный результат. Универсальные регулятивные действия: составлять план, алгоритм решения задачи, выбирать способ решения с учётом имеющихся ресурсов и собственных возможностей, аргументировать и корректировать варианты решений с учётом новой информации. |
| Предметные: свободно оперировать понятием: тригонометрическое уравнение; применять необходимые формулы для решения основных типов тригонометрических уравнений, выполнять отбор корней на заданном отрезке. Применять графические методы для решения уравнений. Свободно оперировать понятиями: графики тригонометрических функций. |
| Ключевые слова: тригонометрические уравнения, графики тригонометрических функций, отрезок. |
3. БЛОЧНО-МОДУЛЬНОЕ ОПИСАНИЕ УРОКА
| БЛОК 1. Вхождение в тему урока и создание условий для осознанного восприятия нового материала |
| Этап 1.1. Мотивирование на учебную деятельность |
|
Фронтальная работа ( обращение к классу): В едином государственном экзамене по профильной математике, во второй части, есть задание, в котором нужно решить тригонометрическое уравнение и сделать отбор корней на определенном отрезке. Это номера №12: правильно выполнили в нашем районе 23,7%, частично выполнили 2,6%. Существуют несколько методов решений тригонометрических уравнений и отбора корней. И стоит владеть ими всеми, так как они используются в зависимости от: вида уравнения; периода и т.д. Так или иначе, у каждого способа есть свои плюсы и минусы в использовании. Но всё же среди всего перечня методов, есть те, которые не пользуются большим спросом. Например: графический.
|
| Этап 1.2. Актуализация опорных знаний |
| Создание ННайдите корни уравнения на заданном отрезке: sinx= , x , x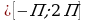 :sinx= :sinx= x1=arcsin x1=arcsin +2Пk, k +2Пk, k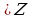 x2=П-arcsin +2Пk, k +2Пk, k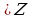 . Как наглядно увидеть корни уравнения? Каким способом выбрать корни на заданном отрезке? . Как наглядно увидеть корни уравнения? Каким способом выбрать корни на заданном отрезке?
|
|
|
| Этап 1.3. Целеполагание |
| Вы научитесь выполнять отбор корней тригонометрических уравнениях на заданном отрезке графическом способом |
| БЛОК 2. Освоение нового материала |
| Этап 2.1. Осуществление учебных действий по освоению нового материала |
| Д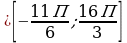 иалоговое объяснение нового материала. иалоговое объяснение нового материала. Задание: Решите уравнение sinx + cosx = 1, и найдите корни на заданном отрезке: х
|
| Этап 2.2. Проверка первичного усвоения |
| После выполнения каждый самостоятельно составляет план-алгоритм для выбора корней уравнения на заданном отрезке графическим способом.
|
| БЛОК 3. Применение изученного материала |
| Этап 3.1. Применение знаний, в том числе в новых ситуациях |
|
Работа в группах: предлагается каждой группе решить тригонометрическое уравнение, но отбор корней на заданном отрезке выполнить разными способами. Каждая группа представляет свой способ. После выполнения задания проанализировать какой из способов был более рациональным.
|
| Этап 3.2. Выполнение межпредметных заданий и заданий из реальной жизни |
|
Тело брошено под углом 60º к горизонту со скоростью 30 м/с. Определите скорость тела через 2 с после начала движения . Сопротивление воздуха пренебрежимо мало. Ускорение свободного падения равно 10 м/. 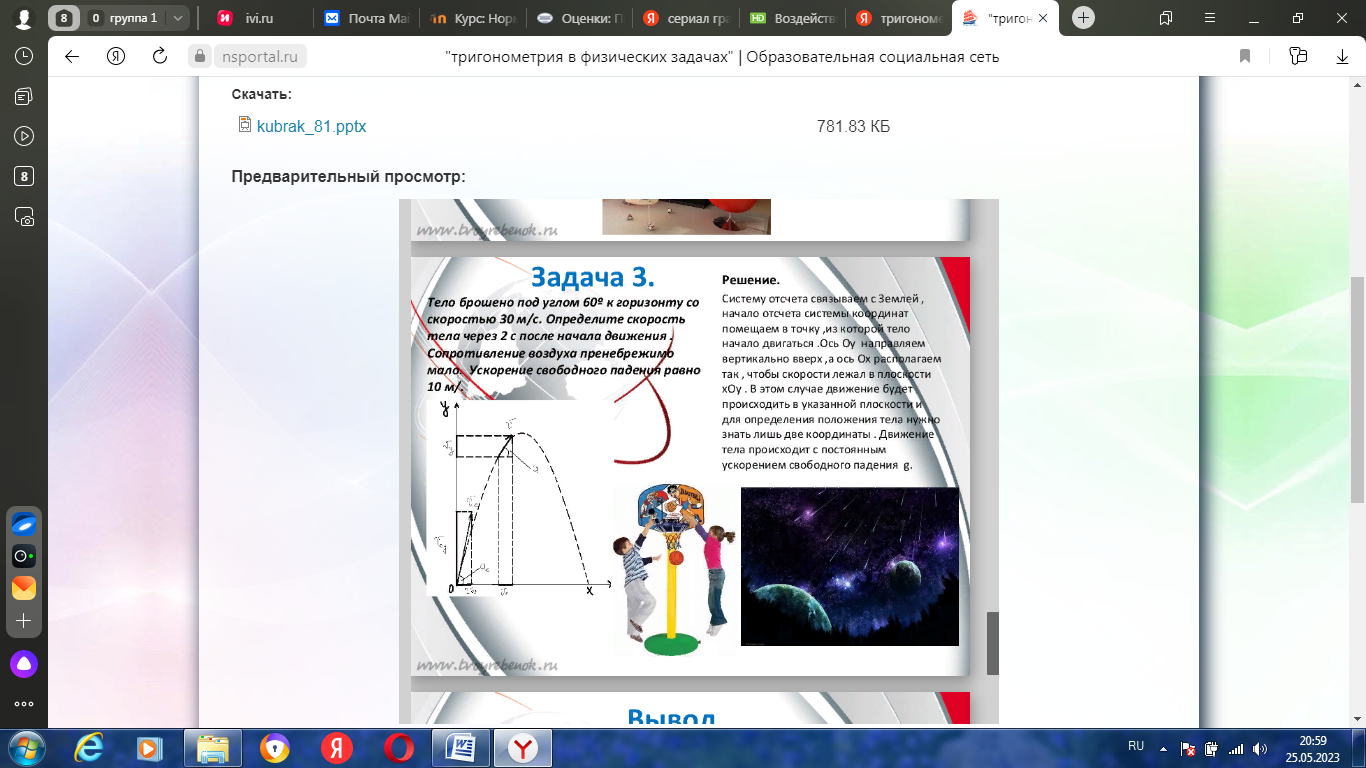
|
| Этап 3.3. Выполнение заданий в формате ГИА (ОГЭ, ЕГЭ) |
|
а) Решите уравнение: sin2x + cos2x + cos2x = 0 б) Выбрать корни на отрезке 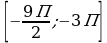
|
| Этап 3.4. Развитие функциональной грамотности |
| Решите уравнение cos2x + sin2 x = 0,5 Найдите корни этого уравнения, принадлежащие отрезку 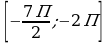
Для данного, задание используют ранее изученный материал: применение тригонометрических формул. |
| Этап 3.5. Систематизация знаний и умений |
| а)Решите уравнение cos2x = 1 – cos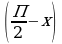 б) Найдите корни этого уравнения, принадлежащие отрезку 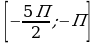
|
| БЛОК 4. Проверка приобретенных знаний, умений и навыков |
| Этап 4.1. Диагностика/самодиагностика |
| -Каких знания нужны для данного способа отбора корней? -Расскажите алгоритм для выбора корней уравнения на заданном отрезке графическим способом. -Какие у вас были затруднения на этом уроке? -Нашли ли вы выход из затруднения? -Какая цель была поставлена? Достигли ли мы цели сегодняшнего урока?
|
| БЛОК 5. Подведение итогов, домашнее задание |
| Этап 5.1. Рефлексия |
| Кто доволен своим результатом? Кто может научить отбирать корни тригонометрического уравнения на заданном отрезке графическим способом своих одноклассников? |
| Этап 5.2. Домашнее задание |
|
Решить 3-4 уравнения из банка ЕГЭ, выполнив отбор корней графическим способом. |






 , x
, x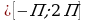 :sinx=
:sinx=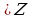
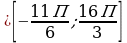 иалоговое объяснение нового материала.
иалоговое объяснение нового материала.