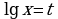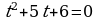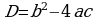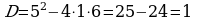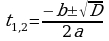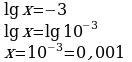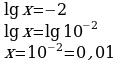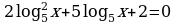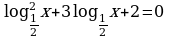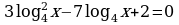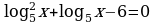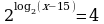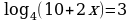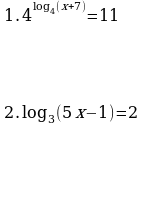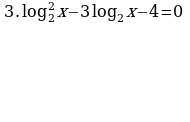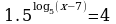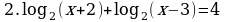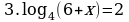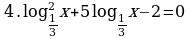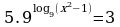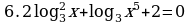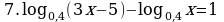Технологическая карта урока
Предмет: математика
Преподаватель: Белова Н.В.
Группа: 13
Дата: 25.04.2025
Цели урока:
- Закрепить понятие логарифма числа.
- Повторить основные свойства логарифма.
- Закрепить умения применять эти свойства и понятия при решении логарифмических уравнений
- Открытие нового метода.
- Систематизация и обобщение знаний по теме.
Воспитательные: Формирование навыков и потребностей умственного труда, убежденности в научных методах исследования, воспитание чувства ответственности и инициативности.
Развивающие: Развитие познавательного интереса к предмету. Формирование ключевых и предметных компетентностей. Развитие творческих способностей.
Задачи урока:
Тренировать способность уметь решать логарифмические уравнения;
Повышать вычислительную культуру обучающихся;
Развивать активную познавательную деятельность обучающихся, интерес к математике, умения преодолевать трудности при решении математических задач.
Воспитывать бережное отношение к своему здоровью, самостоятельность, аккуратность.
Тип урока: комбинированный.
Необходимое техническое оборудование: интерактивная доска, мультимедиа проектор, презентация, диагностическая карта.
СТРУКТУРА И ХОД УРОКА
| Этапы урока | Содержание учебного материала. Деятельность преподавателя | Деятельность студентов |
|
| Организационный (1 мин) | Здравствуйте! Рада видеть вас сегодня. Можете присесть. Проверьте, все ли вы приготовили к уроку, у всех есть ручки и тетради? | Садятся за парты, проверяют свою готовность к уроку, просят недостающие вещи у преподавателя. |
|
| Мотивационный (3-4 мин) | Слова польского математика Георга Цейтена «Правильному применению методов можно научиться только применяя их на разнообразных примерах» будут эпиграфом нашего урока. (Слайд 1). Объявление темы урока. Слайд 2 Постановка целей урока. Слайд 3 Сегодня на уроке вы будете сами оценивать свою учебную деятельность, выполняя задания и набирая баллы. Желаю вам успеха! | Слушают обращение учителя, настраиваются на продуктивную работу. | «3» | «4» | «5» | |
|
| 14-18 баллов | 19-23 баллов | 24-29 баллов |
У каждого студента на столах оценочная карта и итоговая таблица оценки учебной деятельности. |
|
| Актуализация знаний обучающихся (3 мин) | -Какие уравнения вы изучили в школе на уроках математики?
- С какими уравнениями вы познакомились впервые только на занятиях математики в техникуме?
-Дайте определение логарифмического уравнения.
Что нужно знать при решении логарифмического уравнения? - Что такое логарифм. Давайте вспомним эти 2 определения. Перед вами карточка Вставьте нужные слова в предложение на карточке №1
2 определения вынесены на карточки, где записаны определения с пропусками слов. Вставить пропущенные в определениях слова. Проверьте себя и оцените. 1 слово- 1 балл
- Что ещё надо знать, чтоб решить логарифмическое уравнение? | Линейные, квадратные, рациональные, иррациональные,
Тригонометрическими, показательными, логарифмическими уравнениями.
Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим. Определение логарифма. Логарифмом числа в по данному основанию а называется показатель степени, в которую надо возвести это основание, чтобы получить данное число.
Свойства логарифма. |
|
| Математический диктант (5 мин) | Предлагаю вам выполнить математический диктант на знание определения логарифма и его свойств, без которых часто решить уравнения бывает сложно.
Выполнение задания № 1 по теме «Свойства логарифмов». Тест составлен на 2 варианта.
После выполнения теста осуществляется взаимопроверка. Обменяйтесь диагностическими картами и проверьте ответы друг друга.
Поднимите руки, кто справился с заданием без ошибок. |
Учащиеся выполняют задание № 1
|
|
| 3 log 34 = log 4 4 = log 3 1 = log -5 5= log 6 2 + log 6 3 = l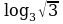 og 2 32 = og 2 32 =
log 2 28 - log 2 7 =
| 5 log 57 = log 4 1= log 6 6 = log 5 (-2)= log 3 27 = l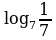 og 2 15 - log 2 30 og 2 15 - log 2 30
log 15 3 + log 15 5 |
| Студенты выполняют взаимопроверку и оценивают свою деятельность.
Поднимают руки. |
| Работа с группой. Опрос, решение у доски (7-8 мин) | - Сколько методов решения логарифмических уравнений вы знаете? - Какие методы решения логарифмических уравнений вы знаете? - Что самое важное при решении логарифмических уравнений? (Найти ОДЗ). - Решить предложенные уравнения. | Отвечают устно, Двое работают у доски, решают уравнения 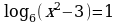
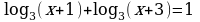
|
|
| Самостоятельная работа по закреплению изученного на прошлом уроке (3-4 мин) | Давайте проверим, как вы усвоили умение решать логарифмические уравнения. Выполнение задания № 2 по теме «Решение логарифмических уравнений». Работа составлена на 2 варианта. | Учащиеся выполняют самостоятельную работу 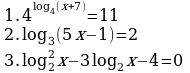
|
|
| Создание проблемной ситуации. (1 мин) | Побуждение к проблеме: – Чего мы еще не знаем?
-Какой возникает вопрос?
| М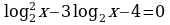 ы не знаем как решать уравнения такого вида. ы не знаем как решать уравнения такого вида.
Как решать логарифмическое уравнение такого вида? |
|
| Формирование проблемы: тема урока. 1 мин | -На какое уравнение похоже логарифмическое уравнение данного вида? -Каким образом нам из этого уравнения получить квадратное? | -Данное уравнение похоже на квадратное уравнение.
-Ввести новую переменную. |
|
| Работа по новой теме урока 1 мин | - Введя новую переменную как дальше решать это уравнение?
-Как найти дальше неизвестную исходного уравнения? -Какие уравнения надо решить при этом? -Какими должны быть допустимые значения неизвестной переменной х? | «Решение логарифмических уравнений методом введения новой переменной»
Научиться решать логарифмические уравнения методом введения новой переменной.
Надо решить квадратное уравнение относительно новой переменной. Из подстановки найти неизвестную первоначального уравнения. Надо решить простейшие логарифмические уравнения. Значения неизвестной переменной х должны быть положительными. |
|
| Решение логарифмического уравнения у доски 5 мин | Преподаватель направляет действия студента при необходимости, выделяет основные моменты. Вопросы которые могут быть заданы (как студенту у доски, так и студентам решающим уравнение на местах): -Какое обозначение мы введём? -Какое уравнение мы получим? -Чему равны коэффициенты квадратного уравнения? -Назовите формулу дискриминанта. -Назовите формулу корней квадратного уравнения? -Какой метод применяем при решении простейших логарифмических уравнений? -Все ли корни являются решением данного уравнения?
Дополнительные вопросы: -Каким методом мы решали уравнение? -Что надо знать и уметь, для того, чтобы решить это уравнение? | У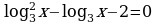 чащиеся записывают решение чащиеся записывают решение уравнения в тетрадь 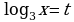
Обозначим: П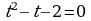 олучим квадратное уравнение: олучим квадратное уравнение:
В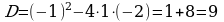 ычислим дискриминант ычислим дискриминант
Н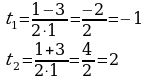 айдём корни квадратного уравнения айдём корни квадратного уравнения
Решим простейшие логарифмические уравнения: 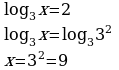 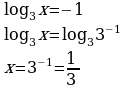
Оба корня положительные, являются решением уравнения. Ответ: х1 = 1/3, х2 = 9 Уравнение решено методом введения новой переменной. Знать формулу дискриминанта, корней квадратного уравнения, определение логарифма. Уметь решать квадратное уравнение и простейшие логарифмические уравнения.
|
|
| Первичное закрепление 5 мин | Организуется усвоение учащимися нового метода решения уравнений. У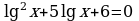 чащимся предлагается решить уравнение чащимся предлагается решить уравнение Ход мыслей обучающихся направляется вопросами: Какое обозначение мы введём? -Какое уравнение мы получим? -Чему равны коэффициенты квадратного уравнения? -Как найти дискриминант? -Вычислите дискриминант. -Чему равен дискриминант? -Сколько корней имеет квадратное уравнение? -Как найти корни квадратного уравнения? -Вычислите корни квадратного уравнения
-Какие получились корни квадратного уравнения? -Что дальше надо сделать? -Каким образом?
-Решим первое уравнение. -Как можно представить «-3» с учётом того, что в левой части десятичный логарифм? -Переведём в десятичную дробь. -Решим второе уравнение. -Как можно представить «-2» с учётом того, что в левой части десятичный логарифм? -Переведём в десятичную дробь. -Все ли корни являются решением данного уравнения? -Какой ответ запишем? -Каким методом мы решали уравнение? -Что надо знать и уметь, для того, чтобы решить это уравнение?
|
Обучающие на местах записывают решение в тетрадь комментируя то, что они записывают.
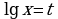
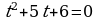
а = 1, в = 5, с = 6 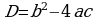
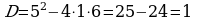
Уравнение имеет 2 корня. 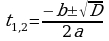
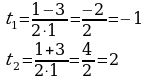
Найти х. Вспомнить обозначение и решить простейшие логарифмические уравнения. 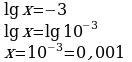
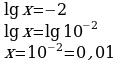
Оба корня положительные.
Ответ: х1 = 0,001, х2 = 0,01 Уравнение решено методом введения новой переменной. Знать формулу дискриминанта, корней квадратного уравнения, определение логарифма. Уметь решать квадратное уравнение и простейшие логарифмические уравнения. |
|
| Включение новых знаний в систему знаний. Укажите метод решения. 3 мин | Какие методы решения логарифмических уравнений вы знаете? Учащимся предлагается выполнить тест № 2: назвать методы решения уравнений и самостоятельно проверить.
| Решение уравнений по определению логарифма. Решение уравнений по свойствам логарифма. Решение уравнений заменой переменной.
|
|
| Подведение итогов 2 мин | Подсчитайте количество набранных Вами баллов и оцените свою деятельность на уроке. | Обучающиеся подсчитывают количество баллов набранных за урок. | «3» | «4» | «5» | |
|
| 14-18 баллов | 19-23 баллов | 24-29 баллов |
|
|
| Рефлексия | - Как вы работали сегодня на уроке? 1) Дайте оценку своей деятельности на уроке: - Я работал отлично, в полную силу своих возможностей, Чувствовал себя уверенно. - Я работал хорошо, но не в полную силу, испытывал чувство неуверенности, боязни, что отвечу неправильно. - У меня не было желания работать. Сегодня не мой день.
2) С каким настроением вы уходите с урока? Приклейте на свою диагностическую карту стикер соответствующего цвета (прием «Светофор»): - красный- тревожно, тему не понял; - желтый- спокоен, скорее понял, чем нет: - зеленый- понял всю тему, уверен, что смогу решить самостоятельную работу. | Студенты дают оценку своей деятельности на уроке. - Я работал отлично, в полную силу своих возможностей, Чувствовал себя уверенно. - Я работал хорошо, но не в полную силу, испытывал чувство неуверенности, боязни, что отвечу неправильно. - У меня не было желания работать. Сегодня не мой день. |
|
| Домашнее задание | Преподаватель комментирует домашнее задание, на следующий урок. | Студенты получают карточки с домашним заданием
|
|
| Логическое завершение урока | Преподаватель благодарит студентов за плодотворную совместную работу на уроке: Окончен урок. Всем спасибо за работу. | Психологический настрой на подведение итогов урока |
|
| Домашнее задание. Решить уравнения | Домашнее задание. Решить уравнения | Домашнее задание. Решить уравнения |
| Домашнее задание. Решить уравнения | Домашнее задание. Решить уравнения | Домашнее задание. Решить уравнения |
| Домашнее задание. Решить уравнения | Домашнее задание. Решить уравнения | Домашнее задание. Решить уравнения |
| Домашнее задание. Решить уравнения | Домашнее задание. Решить уравнения | Домашнее задание. Решить уравнения |
Оценочная карта студента. (1В)_______________________________________________________
Математический диктант.
| Примеры | Ответы | 1/0 | Критерии оценивания:
|
3 log 34 = log 4 4 = log 3 1 = log -5 5= log 6 2 + log 6 3 = l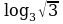 og 2 32 = og 2 32 = log 2 28 - log 2 7 = |
|
| За правильно выполненное задание 1 балл. |
Решение уравнений.
|
| Критерии оценивания: |
| 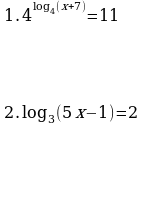
| 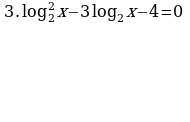
| 2 балла
3 балла
4 балла
|
Укажите метод решения.
| Уравнение | Ответы | 1/0 | Количество баллов |
| 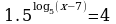
|
|
| За правильно выполненное задание 1 балл. |
| 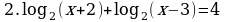
|
|
|
| 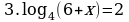
|
|
|
| 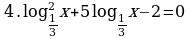
|
|
|
| 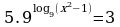
|
|
|
| 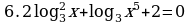
|
|
|
| 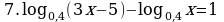
|
|
|
Общее количество баллов:_____________Оценка_________________
Оценочная карта студента. (2В)________________________________________________________
Математический диктант.
| Примеры | Ответы | 1/0 | Критерии оценивания:
|
5 log 57 = log 4 1= log 6 6 = log 5 (-2)= log 3 27 = l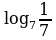 og 2 15 - log 2 30 = og 2 15 - log 2 30 = log 15 3 + log 15 5 |
|
| За правильно выполненное задание 1 балл. |
Решение уравнений.
|
| Критерии оценивания: |
| 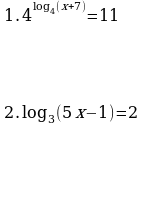
| 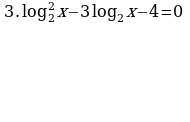
| 2 балла
3 балла
4 балла |
Укажите метод решения.
| Уравнение | Ответы | 1/0 | Количество баллов |
| 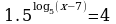
|
|
| За правильно выполненное задание 1 балл. |
| 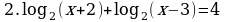
|
|
|
| 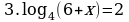
|
|
|
| 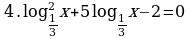
|
|
|
| 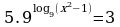
|
|
|
| 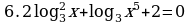
|
|
|
| 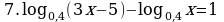
|
|
|
Общее количество баллов:_____________Оценка_________________
Карточка № 1
Фронтальный опрос
Вставьте в определение недостающие слова.
Уравнение, содержащее ……………... под знаком ………….……., называется логарифмическим logax=b, где a 0, a … 1.
Логарифмом числа b по ……………. а называется ……………. степени, в которую нужно ……………….. основание a, чтобы получить число b.
За каждый правильно заполненный пробел запишите по 1 баллу.
Итого:
Рефлексия
Дайте оценку своей деятельности на уроке:
- Я работал отлично, в полную силу своих возможностей, Чувствовал себя уверенно.
- Я работал хорошо, но не в полную силу, испытывал чувство неуверенности, боязни, что отвечу неправильно.
- У меня не было желания работать. Сегодня не мой день.
С каким настроением вы уходите с урока?
Приклейте на свою оценочную карту стикер соответствующего цвета (прием «Светофор»):
- красный- тревожно, тему не понял;
- желтый- спокоен, скорее понял, чем нет:
- зеленый- понял всю тему, уверен, что смогу решить самостоятельную работу.







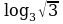 og 2 32 =
og 2 32 =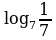 og 2 15 - log 2 30
og 2 15 - log 2 30 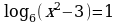
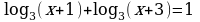
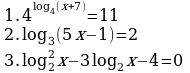
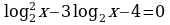 ы не знаем как решать уравнения такого вида.
ы не знаем как решать уравнения такого вида.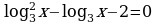 чащиеся записывают решение
чащиеся записывают решение 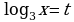
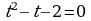 олучим квадратное уравнение:
олучим квадратное уравнение: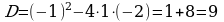 ычислим дискриминант
ычислим дискриминант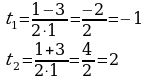 айдём корни квадратного уравнения
айдём корни квадратного уравнения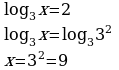
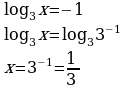
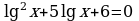 чащимся предлагается решить уравнение
чащимся предлагается решить уравнение