| 1. Организационный момент
| Здравствуйте, ребята. На экране появляется текст: Эпиграф: «Математика представляет искуснейшие изобретенья, способные удовлетворить любознательность, облегчить ремесла и уменьшить труд людей.» (Р.Декарт) Девиз урока: «Временная неудача лучше временной удачи». (Пифагор) - Как вы понимаете эти слова. | Проверяют готовность своего рабочего места. Делают записи в тетрадях.
| Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.
|
| 2. Постановка темы и учебной цели урока | - Вспомните, пожалуйста, тему прошлого урока. Сегодня мы продолжим работу над этой темой. - Исходя из этого, сформулируйте цель нашего урока. | Участвуют в беседе с учителем, отвечают на поставленные вопросы.
| Регулятивные: целеполагание. Коммуникативные: постановка вопросов. Познавательные: самостоятельное выделение-формулирование познавательной цели; логические - формулирование проблемы. |
| 3. Актуализация знаний | 1. Проверка домашнего задания. - Какие вопросы возникли при выполнении работы дома? 2. Работа по индивидуальным карточкам. I уровень. В треугольнике АВС АВ=6м, АС=8м, 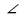 А=60°. Найти ВС. А=60°. Найти ВС. Ответ: 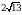 м. м. II уровень. Решить треугольник АВС, если АС=5, ВС=12, 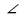 А=120°. А=120°. Ответ: 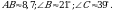 III уровень. В параллелограмме ABCD АВ=5, AD=8, диагональ BD равна 9. Найдите диагональ АС. Ответ: 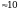 3. Блиц-опрос: 1) С помощью каких приборов измеряют небольшие расстояния, углы? 2) Какие основные теоремы применяются во время решения треугольников? Сформулируйте их. 3) Какой вид имеет треугольник со сторонами 6м,8м,10м? 4) Какой вид имеет треугольник со сторонами 2м,4м,5м? 5) Какой вид имеет треугольник со сторонами 8м,10м,12м? 6) В треугольнике АВС А=32° , В=63°. Какая из сторон является наибольшей? 7) В треугольнике АВС АВ=5м, ВС=6м, АС=7м. Какой из углов является наименьшим? 4. Коллективное решение задачи. В треугольнике АВС А=20° , В=40°, АВ=12см. Найдите радиус окружности, описанной около этого треугольника. Ответ: 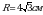 | Два ученика готовят на доске краткое решение задач.
Три ученика индивидуально выполняют задания по карточкам.
Остальные учащиеся отвечают на вопросы учителя.
Решают задачу. | Регулятивные: самоконтроль: учатся отличать верно выполненное задание от неверного; осознание, что уже усвоено и что ещё нужно усвоить, осознание качества и уровня усвоения. Коммуникативные: умение выражать свои мысли с достаточной полнотой и точностью; умение слушать и понимать речь других. Познавательные: формирование мыслительной операции: анализ, сравнение. |
| 4. Мотивация учебной деятельности. | Тригонометрические формулы используются при проведении различных измерительных работ на местности. Например, при измерении высоты предмета и измерении расстояния до недоступной точки. Есть профессии, которые требуют часто выполнять решение треугольников. - Как вы думаете, какие? В первую очередь этим занимаются геодезисты. Когда намечается большая стройка, первыми работу начинают геодезисты, чтобы снять план местности и охарактеризовать рельеф. Когда же на основании их исследований в проектных организациях обработают проект, геодезисты снова меряют углы, решают треугольники, забивают колышки – «привязывают» обработанный проект к местности. - А зачем они решают треугольники? Чтобы определить нужные расстояния, не измеряя их непосредственно. Есть еще специалисты, которые решают подобные задачи в шахтах, туннелях, метро и других подземных объектах. Это маркшейдеры. Им также часто приходится решать треугольники. Сегодня на уроке мы будем решать практические задачи с применением теорем синусов и косинусов. | Слушают учителя. Отвечают на вопросы. Задают вопросы. | Коммуникативные: умение выражать свои мысли с достаточной полнотой и точностью; умение слушать и понимать речь других. |
| 5. Решение практических задач. | Коллективная работа. Задача 1. 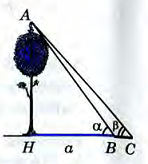 Найдите высоту дерева, если а=10м, Найдите высоту дерева, если а=10м, 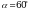 Ответ: 5,6м. Задача 2. Вершина горы видна из точки А под углом 38°, а при приближении к горе на 200 м вершина стала видна под углом 42°. Найти высоту горы. 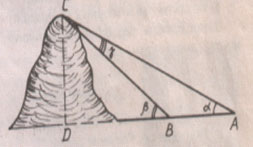 2. Работа в дифференцированных группах. Группа 1. Для измерения расстояния между опорами А и В высоковольтных линий, которые разделены водой, выбрали пункт С и измерили СА=40 м., СВ=20 м., 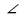 АСВ=95°. Найдите АВ. АСВ=95°. Найдите АВ.
  А В А В

С Дано: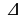 АВС, СА=40м,СВ=20 м, АВС, СА=40м,СВ=20 м, 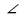 АСВ=95°. АСВ=95°. Решение. По теореме косинусов: АВ2=АС2+СВ2- 2АС*СВ*cos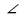 С С АВ2=2139,52, АВ= 46,3 м. Ответ: 46,3м.
Группа 2. Определите ширину реки, если башня, высота которой 65м, находится на берегу реки и ее видно с другого берега под углом 70°.  А А
  В С В С
Дано: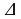 АВС, АВС,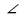 В=90°, АВ=65м, В=90°, АВ=65м, 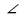 С = 70°. С = 70°. Найти: ВС. Решение: ВС = АВ*ctg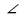 C, C, ВС= 65* 0,364= 23,66м. Ответ: 23,66м
Группа 3. Найти расстояние между двумя недоступными предметами В и С, которые находятся на противоположных берегах реки, если АС=8м, 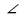 С=35°, С=35°,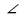 А=70°. А=70°.
  В В
 Дано: Дано: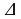 АВС, АС=8м, АВС, АС=8м,
 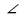 А=70°, А=70°,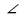 С =35°. С =35°.
Найти: ВС.
А С
Решение:
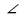 В=180°-70°-35°= 75°. В=180°-70°-35°= 75°.
По теореме синусов: 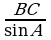 = =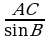 ; ВС= ; ВС=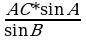 ; ВС=8*0,9397/0,9659=7,78(м). ; ВС=8*0,9397/0,9659=7,78(м).
Ответ:7,78м. Группа 4. Найти расстояние от острова В, расположенного на озере до пункта А, который находится на берегу, если расстояние АС=18м и углы 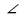 А=100°, А=100°, 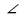 С=50°. Остров принять за точку. С=50°. Остров принять за точку. 
  
В в
 С С
А Дано: 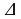 АВС, АС=18м, АВС, АС=18м, 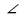 А=100°, А=100°,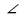 С = 50°. С = 50°. Найти: AB
Решение: 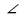 В=180° – 150°=30°. В=180° – 150°=30°.
По теореме синусов: 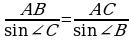 ; АВ= ; АВ=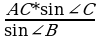 ; ; АВ=18*0,766/0,5=27,58 (м). Ответ:27,58м.
| Решают задачи.
Работают в группе, обсуждают методы решения, оформляют решение в тетрадях. Выбирают представителя от группы для представления своего решения у доски.
Каждая группа отчитывается об итогах работы. Для ответа возле доски выступает представитель группы. Учащиеся объясняют решение задач, записывают решения в тетради, обмениваются задачами.
| Регулятивные: проговаривание; формирование познавательной инициативы Познавательные: умения делать предположения и обосновывать их; структурирование знаний, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия. Коммуникативные: умение выражать свои мысли с достаточной полнотой и точностью; умение слушать и понимать речь других; учитывать разные мнения |
| 6. Подведение итогов урока.
| Подведение итогов. 1) Какая группа быстро и правильно выполнила задание? 2) Как работал класс? 3) Как работали отдельные учащиеся? 4) Оценки тем, кто защищал задачу, кто принимал активное участие в обсуждении. | Слушают учителя, обсуждают свою работу и работу одноклассников на уроке, вносят свои предложения.
| Регулятивные: оценка, контроль, коррекция. |





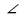 А=60°. Найти ВС.
А=60°. Найти ВС.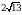 м.
м.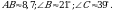
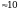
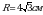
 Найдите высоту дерева, если а=10м,
Найдите высоту дерева, если а=10м, 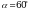


 А В
А В 
 АВС, СА=40м,СВ=20 м,
АВС, СА=40м,СВ=20 м,  А
А 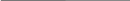
 В С
В С АВС,
АВС,
 В
В  Дано:
Дано:
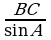 =
=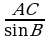 ; ВС=
; ВС=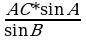 ; ВС=8*0,9397/0,9659=7,78(м).
; ВС=8*0,9397/0,9659=7,78(м).



 С
С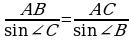 ; АВ=
; АВ=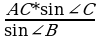 ;
;









