| Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий, умеют формулировать и доказывать теорему о внешнем угле треугольника | Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют работать в сотрудничестве с учителем. Личностные: проявляют критичность мышления, инициативу, находчивость, активность при решении геометрических задач |
| Ввести понятие внешнего угла и доказать сопутствующую теорему | (Ф/И) 1. Ввести понятие внешнего угла треугольника. 2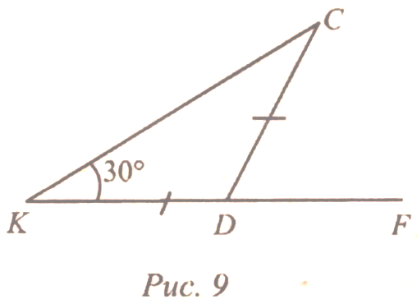 . Доказать теорему о внешнем угле треугольника (рис. 131 учебника). . Доказать теорему о внешнем угле треугольника (рис. 131 учебника). 3. Решить задачу (устно). В треугольнике АВС В = 110. Чему равны: а) сумма остальных внутренних углов треугольника; б) внешний угол при вершине В? 4. По готовому чертежу на доске устно решить задачу. Найдите внутренние углы и внешний угол СDF треугольника KCD
|
| При решении простейших задач отработать изученный материал | (Ф/И) Организует деятельность учащихся. 1. Решить задачи № 237 под руководством учителя на доске и в тетрадях. 2. Рассмотреть обратное утверждение: если треугольник равнобедренный, то внешний угол при вершине, противолежащей основанию треугольника, в два раза больше угла при основании. Действительно, этот внешний угол равен сумме двух углов при основании равнобедренного треугольника, а так как углы при основании равны, то данный внешний угол в два раза больше угла при основании треугольника. 3. Решить задачу № 239 на доске и в тетрадях (рассмотреть два случая) |  № 237. Д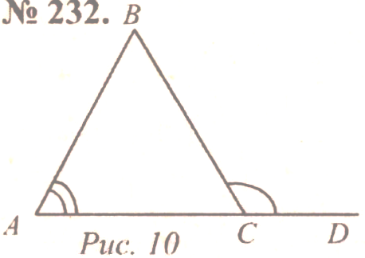 ано: АВС, ВСD A в 2 раза ано: АВС, ВСD A в 2 раза Доказать: АВС – равнобедренный. Доказательство: Пусть А = х, тогда ВСD = 2х. По свойству внешнего угла: ВСD = А + В, тогда 2х = х + В, В = х. Значит, А = В, то есть АВС – равнобедренный. Обратное утверждение верно. № 239. I случай случай Дано: АВС, АВ = ВС, ВСD = 115. Найти: А, В, С. Решение: 1) C и BСD – смежные, значит, С = 180 – 115 = 65, 2) А = С = 65 (по свойству равнобедренного треугольника) 3) В = 180 – (А + С). В = 180 – 130 = 50. Ответ: 65, 50, 65. II случай Дано: АВС, АВ = ВС, СВD = 115. Найти: А, В, С. Р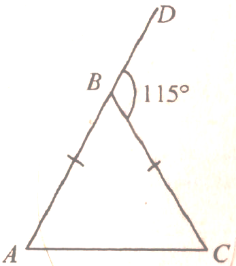 ешение: ешение: 1) В и СВD – смежные, значит, В = 180 – 115 = 65, 2) А = С (по свойству равнобедренного треугольника) А = С = (180 – 65) : 2 = 57,5 = 5730. Ответ: 5730, 65, 5730. |
| Совершенствовать навыки самостоятельного решения задач | (И) Работа выполняется 15-20 минут. Вариант I 1. Один из углов равнобедренного треугольника равен 96. Найдите два других угла треугольника. 2. В треугольнике CDE с Е = 32 проведена биссектриса CF, CFD = 72. Найдите D. Вариант II 1. Один из углов равнобедренного треугольника равен 108. Найдите два других угла треугольника. 2. В треугольнике CDE проведена биссектриса CF, Е = 32, D = 68. Найдите CFD. Вариант III 1. В равнобедренном треугольнике MNP с основанием MP и N = 64 проведена высота MH. Найдите PMH. 2. В треугольнике CDE проведены биссектрисы CК и DP, пересекающиеся в точке F, причем DFK = 78. Найдите CFD. Вариант IV 1. В равнобедренном треугольнике CDE с основанием CE и D = 102 проведена высота CH. Найдите DCH. 2. В треугольнике ABC проведены биссектрисы AM и BN, пересекающиеся в точке K, причем AKN = 58. Найдите ACB.
|







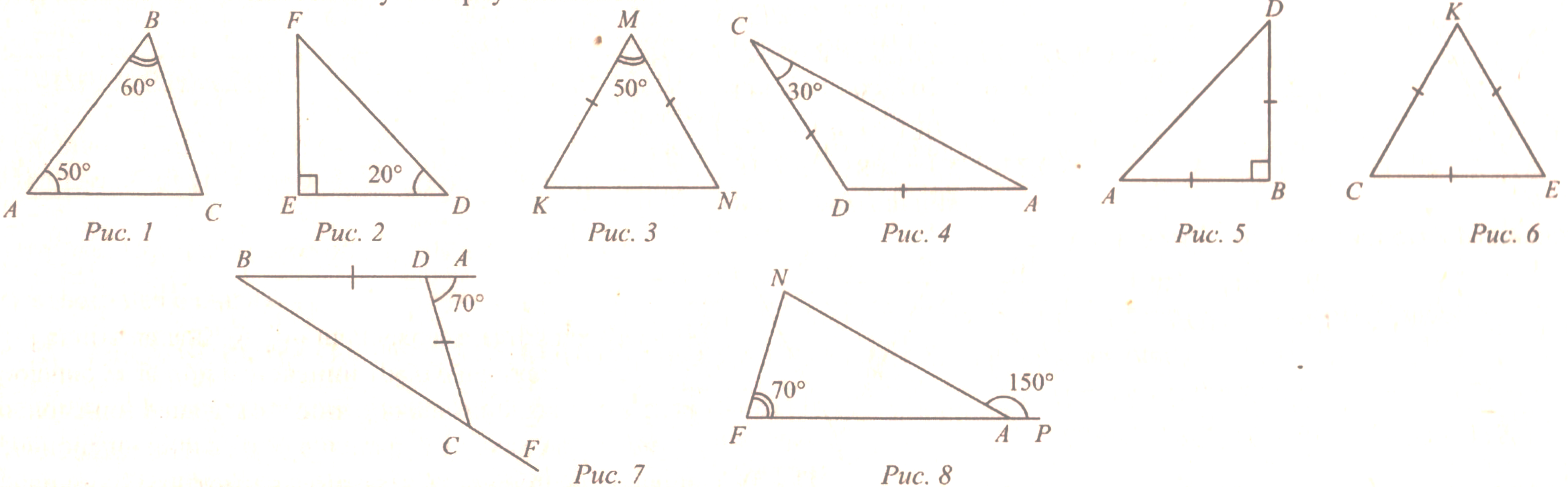
 . Доказать теорему о внешнем угле треугольника (рис. 131 учебника).
. Доказать теорему о внешнем угле треугольника (рис. 131 учебника).
 ано: АВС, ВСD A в 2 раза
ано: АВС, ВСD A в 2 раза случай
случай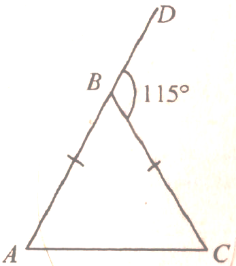 ешение:
ешение:









