Тема урока"Размещения"

Задача

• 1.Сколькими способами можно составить расписание на день из шести различных уроков, если изучается 14 предметов?

Задача

• В футбольной команде 11 человек, нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?

Размещения .

11 класс

Цели урока:

-Развивать логическое мышление, память, внимание, умение сравнивать и обобщать.

-Развивать умения работать в группе, формировать чувство ответственности за принятое решение.

Работа с учебником

• № 1077(1,3,5,7) ,№1099(2,4)

Дополнительная задача.

• Сколькими способами могут занять первое, второе и третье места 8 участниц финального забега на 100м?

Самостоятельная работа

Вариант 1

• 1.Здание школы имеет 5 запасных выходов. Сколькими способами можно войти и выйти из здания школы?
• 2 Олеся, Оксана и Юля купили билеты на концерт симфонического оркестра на 1, 2 и 3-е места первого ряда. Сколько существует способов размещения девочек на эти места?
• 3.Сколько существует способов выбрать троих ребят из 11 желающих дежурить по школе?
• 4. Из 26 учащихся класса надо выбрать старосту и его заместителя. Сколькими способами это можно сделать?

Вариант 2

• 1. У Светланы три юбки и 5 кофт, удачно сочетающихся по цвету. Сколько различных комбинаций из юбок и кофт имеется у Светланы?
• 2 Четыре друга купили билеты в кино: на 1-е и 2-е места в первом ряду и на 1-е и 2-е места во втором ряду. Сколькими способами друзья могут занять эти 4 места в кинотеатре?
• 3. Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?
• 4. Сколькими способами могут быть распределены первая, вторая и третья премии между 13 участниками конкурса?

Рефлексия

– урок полезен, все понятно.

– лишь кое-что чуть-чуть неясно, ещё придется потрудиться.

– да, трудно все-таки учиться!

Домашнее задание:

П60-62, №1077(чет.),№1099(2,4), ЕГЭ В- 21

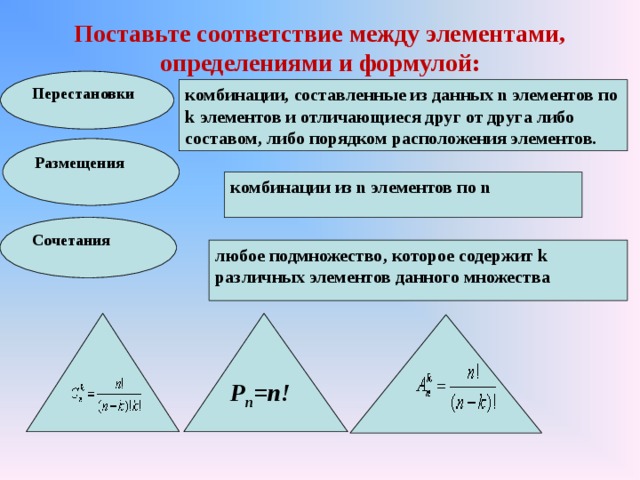
Поставьте соответствие между элементами, определениями и формулой:

Перестановки

комбинации, составленные из данных n элементов по k элементов и отличающиеся друг от друга либо составом, либо порядком расположения элементов.

Размещения

комбинации из n элементов по n

Сочетания

любое подмножество, которое содержит k различных элементов данного множества

P n =n!

Правильный ответ:

P n =n!

Перестановки

комбинации из n элементов по n

комбинации, составленные из данных n элементов по k элементов и отличающиеся друг от друга либо составом, либо порядком расположения элементов.

Размещения

любое подмножество, которое содержит k различных элементов данного множества

Сочетания

Работа в группах

• Придумайте и решите задачу из данных, предложенных в конвертах!

Спасибо за урок !!!!!

Список используемой литературы:

1. http://www.ege-study.ru/ege-materials/ math/probability.html