Теорема Пифагора и ее жизнь

«Теорема Пифагора и её практическое применение»

Содержание

Аннотация

I.  Историческая справка о Пифагоре

II.  Доказательства теоремы Пифагора

III.  Использование теоремы Пифагора в решении задач

IV.  Практическое применение теоремы Пифагора

2)  мобильная связь

V.  Заключение

VII.  Литература

Аннотация

В данном исследовании сделана попытка объединить и систематизировать самые разные стороны применения теоремы Пифагора.
Кроме того, дана историческая справка о личности Пифагора, показаны различные доказательства этой теоремы и решения множества задач по её практическому применению в различных сферах жизни , а также в каком виде теорема Пифагора представлена в различных задачах геометрической части материалов ЕГЭ

Задачи, которые ставит перед собой данная исследовательская работа:

1. показать применение теоремы Пифагора при решении задач из материалов ЕГЭ

· 2) рассмотреть её практическое применение в архитектуре, строительстве,
мобильной связи, астрономии.

В своей исследовательской работе использовали монографии по математике, исследовательские разработки, материалы периодической печати, Интернет-ресурсы, мультимедийные компьютерные технологии. В работе представлен объёмный иллюстративный материал в виде таблиц, чертежей, иллюстраций, фотоснимков, рисунков, математических расчётов. Во всех расчетах оперировали приближёнными числовыми значениями величины, так как первоначальные исходные данные получали путём измерений.

Мы представляем результат работы над проектом в виде электронной презентации. Практическое применение нашей работы – использование нашего проекта для элективных курсов, предпрофильной и профильной подготовках и на факультативных занятиях

Глава I

Историческая справка о Пифагоре

Пифагор Самосский родился около 580 г. до н. э. на острове Самос в Ионическом море. Пифагор – едва ли не самый популярный учёный за всю историю человечества.
Он принимал в свою школу только тех юношей, которые промолчали в течение пяти лет. Значит, при занятиях математикой нужна абсолютная тишина для того, чтобы можно было сосредоточить все внимание на решении того или другого утверждения.
Пифагор был не только учёным, но и основателем первой научной школы. Он был и воспитателем душ, проповедником собственной «пифагорейской» этики, философом, которого по силе духа и силе воздействия можно сравнить разве с его великими современниками: Конфуцием, Буддой. Но в отличие от них Пифагор создал самую яркую «религию». Он воспитывал в человеке веру в могущество разума, убеждённость в познаваемости природы, уверенность в том, что ключом к тайнам мироздания является математика.
2500 лет тому назад Пифагор направил людей по пути торжества разума. Легенды наперебой объявляют Пифагора чудотворцем. Сообщают, что у него было золотое ребро, что люди видели его одновременно в двух разных городах говорящим со своими учениками, что, однажды, когда он с многочисленными спутниками переходил реку и заговорил с ней, река вышла из берегов и громким голосом воскликнула: «ДА здравствует Пифагор!» Сообщали, что в Тиррении он умертвил своим уксусом ядовитую змею, унёсшую многие жизни. Что он предсказывал землетрясения, отвращал ураганы, укрощал морские волны, останавливал повальные болезни. Порфирий рассказывал о Пифагоре такую историю, что в Торренте он увидел быка, жевавшего новые бобы, подошёл к пастуху и посоветовал сказать быку, чтобы тот этого не делал. Пастух засмеялся и сказал, что он не умеет говорить по-бычьи. Тогда Пифагор сам подошёл к быку и прошептал ему что-то на ухо; после чего бык не только пошёл прочь из бобовника, но и никогда не касался бобов. В 1808 году в Санкт-Петербурге вышла карманного формата книжка «Пифагоровы законы и нравственные правила». Вот некоторые извлечения из этой книги, содержащей 325 заповедей.

Глава II

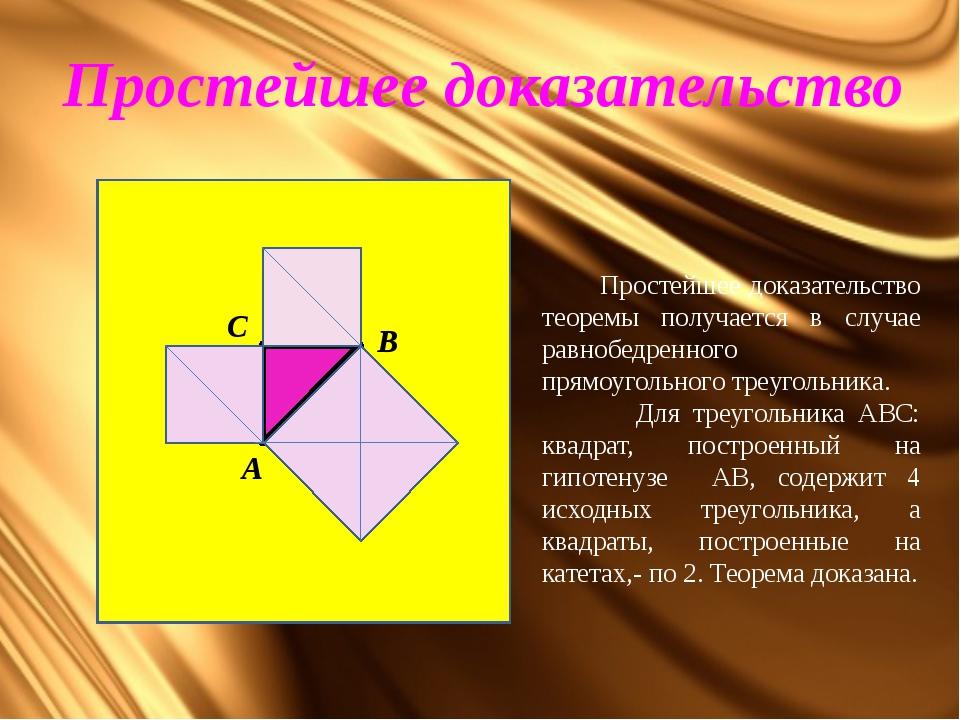
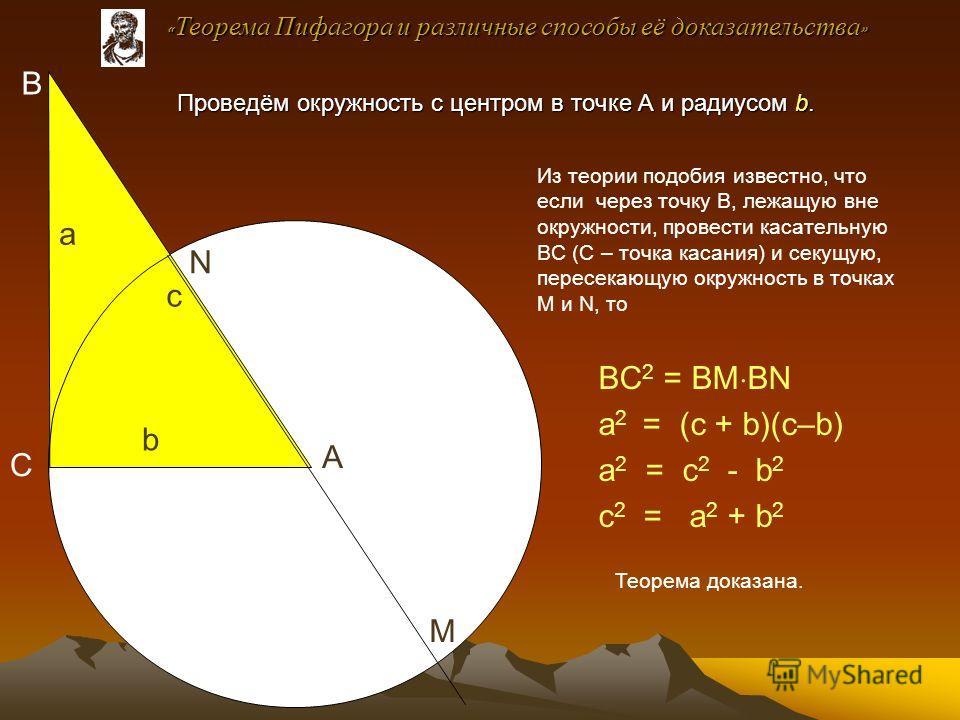
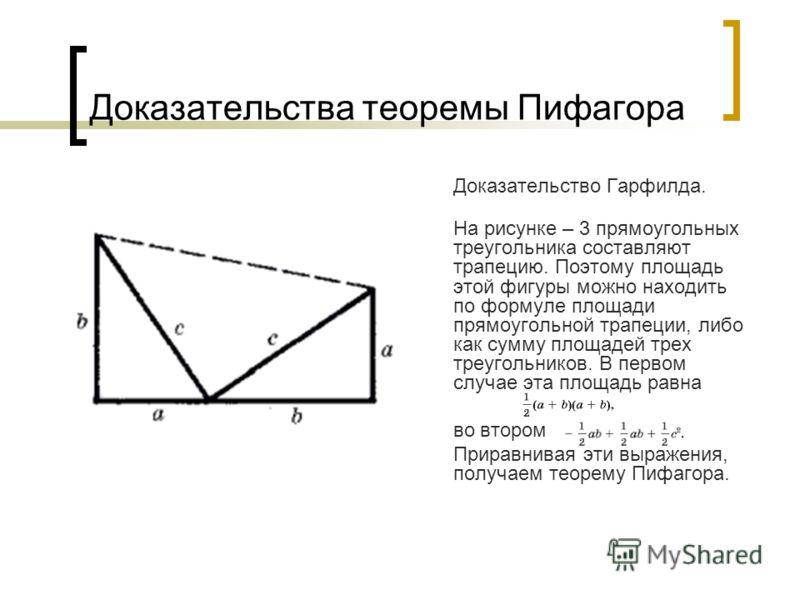
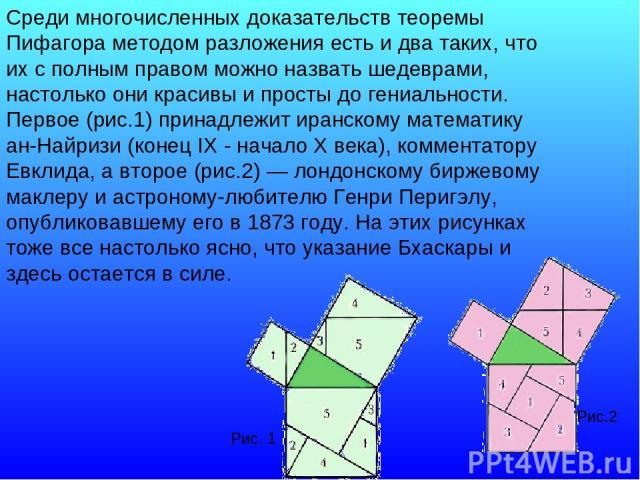
Сегодня известно около 500 различных доказательств теоремы Пифагора геометрических, алгебраических, механических и прочих.

Дано:

Прямоугольный треугольник

а, в – катеты

с- гипотенуза

Доказать: с2=а2+в2

Доказательство:

1) Достроим треугольник до квадрата со

стороной а + в.

2) Sкв= (а+в)2

Sкв=4∙1/2ав+с2=2ав2+с2

Тогда, 2ав2+с2=(а+в)2

2ав2+с2=а2+2ав+в2

Вычтем из обеих частей 2ав, тогда:

с2=а2+в2,что и требовалось доказать.

Глава III

Применение теоремы Пифагора при решении различных задач ЕГЭ

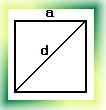1) Диагональ d квадрата со стороной a можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом a. Таким образом,

d2=2*a2
   d=√ 2*a.

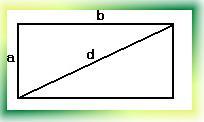
2) Диагональ d прямоугольника со сторонами a и b вычисляется подобно тому, как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Таким образом, мы имеем

d2=a2+b2

Возможности применения теоремы Пифагора к вычислениям не ограничиваются планиметрией; мы сейчас перейдём к пространственным телам и рассмотрим некоторые простейшие из них.
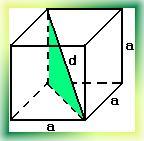
 На рисунке изображён куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника, закрашенного на рисунке. Катетами треугольника служат ребро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина этой диагонали равна (√ 2*a). Отсюда имеем

d2=a2+ (√ 2*a)2
d2=a2+2*a2=3*a2

Рассмотрим применение теоремы Пифагора в базовых задачах Егэ. Одна из классических задач:

1

В треугольнике АВС угол С равен 90°,АВ=5 , sinA=7/25. Найдите АС.

Решение: SINA= BC/AB, отсюда следует пропорция 7/25=ВС/5, имеем ВС=(7*5)/25=7/5

Применяя теорему Пифагора получим АС.

АС= 4,8.

Аналогично решается задача с заданным косинусом и тангенсом угла. Например,

2 В треугольнике АВС угол С равен 90°,АВ=5 , COSA=7/25/ Найти ВС?

3 В треугольнике АВС угол С равен 90°,АВ=7 , TGA= ,найти ВС?

Часто встречаются задачи, которые имеют практическую направленность и решаются только с помощью теоремы Пифагора. Например:

4 Лестница длиной 2,5 м приставлена к стене так, что ее верхний конец находится на высоте 2,4 м от земли. На сколько метров от стены отстоит нижний конец лестницы?

5 У стены под углом 60 градусов к горизонту стоит лестница длиной 2,8 м. На сколько метров отстоит от стены нижний конец лестницы?

Решение этой задачи сводится к решению задачи 1, изложенной выше.

Очень много задач содержат не прямоугольный треугольник, а равнобедренный или равносторонний. Достаточно в таких треугольниках провести высоту, которая является также медианой (делит сторону пополам) и мы имеем опять классическую задачу на решение треугольника с использованием теоремы Пифагора. В основном с такой задачей в ЕГЭ мы сталкиваемся в стереометрии:

-нахождении высоты пирамиды или
- высоты боковой грани ,
- а также некоторые вариации с окружностью
Решаются именно таким образом. Трудность для учащихся состоит в том, что они не имеют достаточное пространственное мышление, чтобы увидеть прямоугольный треугольник, стоящий не так, как они привыкли в средних классах.

Вот некоторые примеры таких задач:

6 В тре­уголь­ни­ке АВС АВ=ВС=24,внеш­ний угол при вер­ши­не С равен 120. Най­ди­те длину ме­ди­а­ны

ВК?

7 Типичная стереометрическая задача на решение прямоугольного треугольника.

В правильной четырехугольной пирамиде SABCD, точка О – центр основания, S- вершина.

SB=13, AC=24. Найти длину отрезка SO?

Радиус основания цилиндра равен 5,а его образующая равна 6. Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 3. Найдите площадь сечения?

Имеем и равнобедренный треугольник, а затем прямоугольный и так далее…

8 Стороны основания правильной четырехугольной пирамиды равны 14, боковые ребра 25. Найти объем ?

Задача находит объем фигуры, но чтобы найти высоту пирамиды, содержащуюся в формуле объема, нам необходимо будет решить задачу на прямоугольный треугольник, причем дважды. Один треугольник рассматривается в основании, для нахождения диагонали квадрата основания, а второй треугольник будет состоять из половины диагонали, боковой стороны и высоты пирамиды.

9 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 8 и 9.
Диагональ параллелепипеда равна 17.Найти объем параллелепипеда.

И опять мы имеем задачу на нахождение объема, формула которого содержит длину, ширину ( в данном случае это два заданных ребра из одной вершины) и высоту, которую мы будем искать, используя диагональ параллелепипеда, как гипотенузу прямоугольного треугольника.

10 В основании прямой призмы лежит прямоугольный треугольник, один из катетов которого равен 4, а гипотенуза равна √65.Найти объем призмы, если высота равна 3.

И опять имеем задачу на нахождение объема фигуры, который равен произведению площади основания на высоту. А чтобы найти площадь основания, а именно площадь прямоугольного треугольника, достаточно найти полу произведение его катетов. Имея один из катетов и гипотезу, найдем другой катет.

АС=√65-16=√49=7

V=(7*4)/2*3=42

Теорема Пифагора имеет широкое применение при изучении смежных дисциплин:

Найдите равнодействующую трёх сил по 200 Н каждая, если угол между первой и второй силами и между второй и третьей силами равен 60°.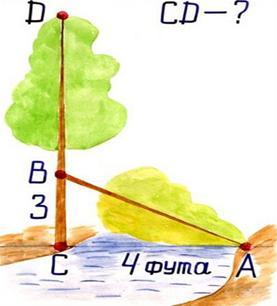

Решение:

 Модуль суммы первой пары сил равен:

F1+22=F12+F22+2*F1*F2cosα

где α-угол между векторами F1 и F2, т. е. F1+2=200√ 3 Н. Как ясно из соображений симметрии вектор F1+2 направлен по биссектрисе угла α, поэтому угол между ним и третьей силой равен:

β=60°+60°/2=90°.

 Теперь найдём равнодействующую трёх сил:

R2=(F3+F1+2 )
R=400 Н.

Ответ: R=400 Н.

Мобильная связь

В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например радиусе R=200 км?, если известно. что радиус Земли равен 6380 км.)

Решение: Пусть AB= x, BC=R=200 км, OC= r =6380 км.
OB = OA + AB
OB = r + x
Используя теорему Пифагора, получим ответ. Ответ: 2,3 км.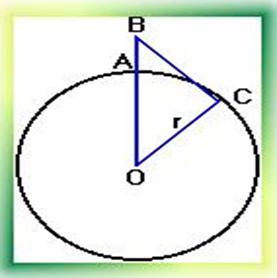

Рассмотрим

случаи применения теоремы Пифагора на практике

.

Пример 1.

В зданиях романского и готического стиля верхние части окон расчленяются каменными рѐбрами, которые не только играют роль орнамента, но и способствуют прочности окон.

В романской архитектуре часто встречается мотив,представленный на этом рисунке.

Рассмотрим, как применяется в таких задачах теорема Пифагора.

Если bобозначает ширину окна, то радиусы полуокружностей будут равны R=b/2 и r =b/4. Радиус р внутренней окружности можно вычислить из прямоугольного треугольника, изображѐнного на рисунке цветом . Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+р, один катет равен b/4, а другой b/2-р.

По теореме Пифагора имеем:

Заключение.

Результат нашей исследовательской работы показал, что теорема Пифагора в настоящее время очень популярна, а причина еѐ популярности заключается в том, что в теореме сочетается простота, красота, значимость.

Работая над исследованием, мы убедились, что теорема Пифагора проста, но не очевидна. Теорема имеет большое

значение: она используется в геометрии практически в каждой задаче, она лежит в основе доказательства множества

других геометрических теорем и имеет большое практическое применение.