Теорема синусов и теорема косинусов

a 2 = b 2 + c 2 − 2 bc cosα

a 2 = b 2 + c 2 − 2 bc cosα

a/ sinA = b/ sin B = c/ sinC

a/ sinA = b/ sin B = c/ sinC

a 2 = b 2 + c 2 − 2 bc cosα .

a 2 = b 2 + c 2 − 2 bc cosα .

Теорема

синусов и

теорема косинусов

a/ sinA = b/ sin B = c/ sinC

a 2 = b 2 + c 2 − 2 bc cosα .

Цель урока

• доказательство теоремы синусов
• доказательство теоремы косинусов
• Применение данных теорем к решению задач

Самостоятельная работа

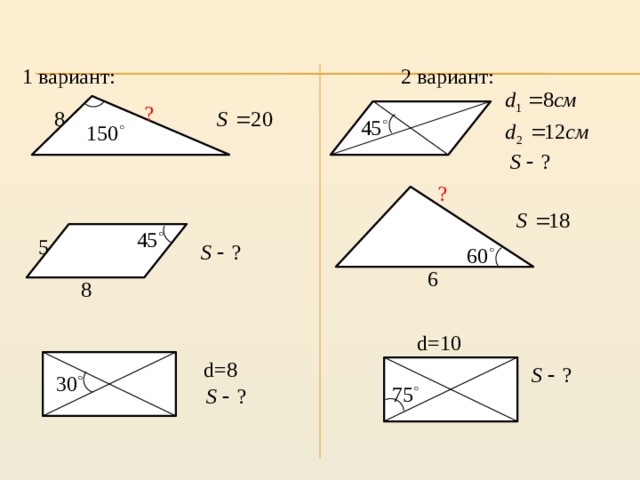
2 вариант:

1 вариант:

?

8

?

5

6

8

d=10

d=8

Проверь ответы:

2 вариант:

1 вариант:

10

8

5

6

8

d=10

d=8

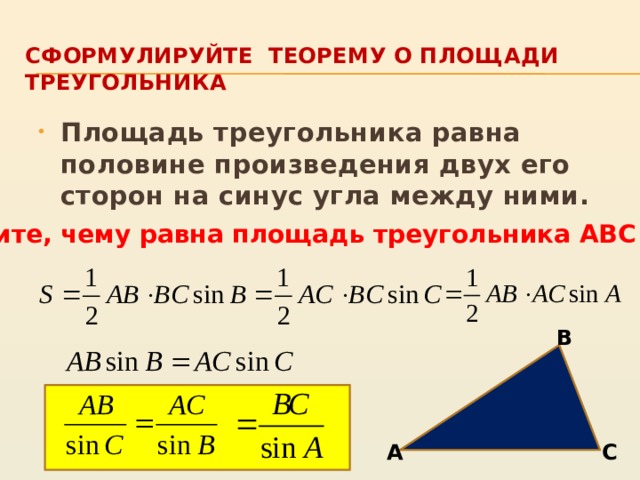
Сформулируйте теорему о площади треугольника

• Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Запишите, чему равна площадь треугольника АВС

В

А

С

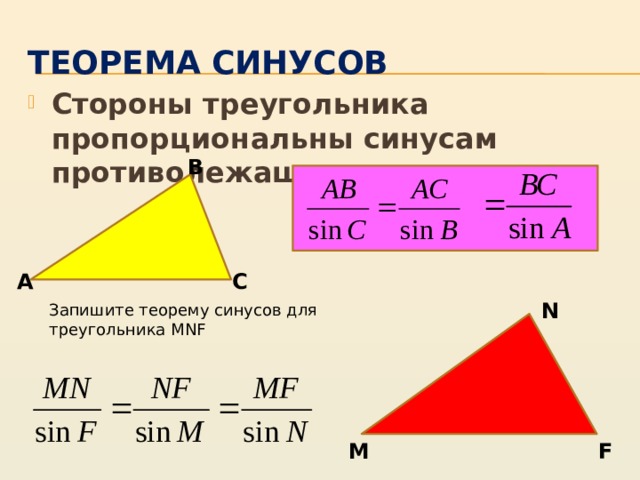
Теорема синусов

• Стороны треугольника пропорциональны синусам противолежащих углов

В

А

С

N

Запишите теорему синусов для треугольника MNF

M

F

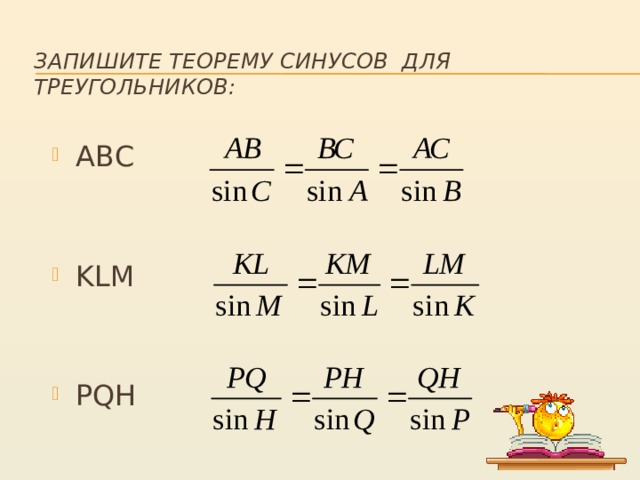
Запишите теорему синусов для треугольников:

• АВС

• KLM

• PQH

Замечание

Отношение стороны треугольника к синусу противолежащего

угла равно диаметру описанной окружности.

ВС= × sin . Если т. лежит на дуге ВАС, то А1= А, если на дуге BDC, то A1= 180° - A. И в том, и в другом случае sin = sin A = BC= *sin A, BC= 2RsinA или " width="640"

Дано:

R – радиус описанной окружности, ВС = a, - диаметр

Доказать:

(BC=2RsinA)

Доказательство:

Проведем диаметр . Рассмотрим , С - прямоугольный =

ВС= × sin . Если т. лежит на дуге ВАС, то А1= А, если на дуге BDC,

то A1= 180° - A.

И в том, и в другом случае sin = sin A = BC= *sin A, BC= 2RsinA или

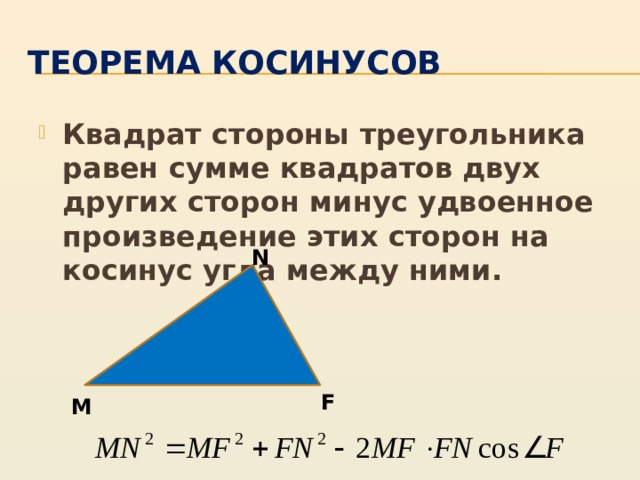
Теорема косинусов

• Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

N

F

M

Доказательство:

Дано:

ΔАВС

АВ=с

АС=b

BC= a

Доказать:

у

(bcos A;bsin A)

С

b

a

c

В

А

(с;0)

(0;0)

х

Запишите теорему косинусов для треугольников:

• АВС

• KLМ

Выразим косинус угла из теоремы косинусов

Выразите

Обобщенная теорема Пифагора.

Теорему косинусов называют иногда обобщенной теоремой Пифагора. Такое название объясняется тем, что в теореме косинусов содержится как частный случай теорема Пифагора. В самом деле, если в ∆АВС угол А прямой, то cos A = cos 90 ° = 0 и

по теореме косинусов a 2 = b 2 + c 2 − 2 bc cosα получаем:

a 2 = b 2 + c 2 ,

т.е. квадрат гипотенузы равен сумме квадратов катетов.

Задача№ 1025 (б)

Дано:

B

Найти:

C

А

Домашнее задание:

• п.п. 1 – 103
• решить №1025 (а,ж,з)

Спасибо за урок