Теория статистических решений.

ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ

(ИГРЫ С ПРИРОДОЙ)

В рассмотренных задачах «Теории игр» предполагалось, что в них принимают участие несколько лиц, действующих сознательно. Интересы некоторых из этих лиц могут совпадать или быть противоположными.

В задачах теории статистических решений также имеется неопределённость, но она вызвана не противодействием противника, а отсутствием информации об условиях, в которых осуществляется принятие решения. Эти условия зависят не от сознательных действий другого игрока, а от объективной действительности, которую принято называть природой. Такие ситуации часто называются играми с природой. Природа мыслится как некая незаинтересованная сторона, поведение которой неизвестно, но, во всяком случае, не злонамеренно.

Например, случайный характер спроса на продукцию делает невозможным точное прогнозирование объёма её выпуска. Принятие решения в этом случае связано с риском. Или, например, приём партии товара для контроля на соответствие стандарту также связан с риском. Правда, неопределённость при контроле может быть устранена в случае контроля всего товара, выпускаемого для реализации. Однако это может оказаться слишком дорогостоящим мероприятием.

Казалось бы, отсутствие сознательного противодействия упрощает задачу выбора решения. Оказывается, нет. В игре против сознательного противника элемент неопределённости отчасти снимается тем, что мы думаем за противника, принимаем за него решение, самое неблагоприятное для нас самих. В игре же с природой такая концепция не подходит: неизвестно, как она себя поведёт.

				…
				…
				…
…		…	…	…	…
				…

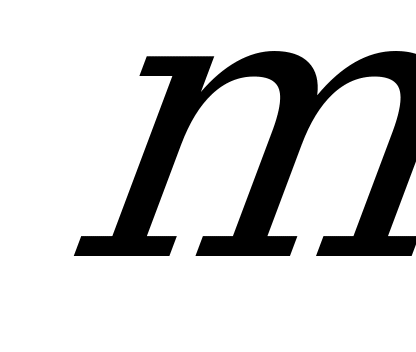
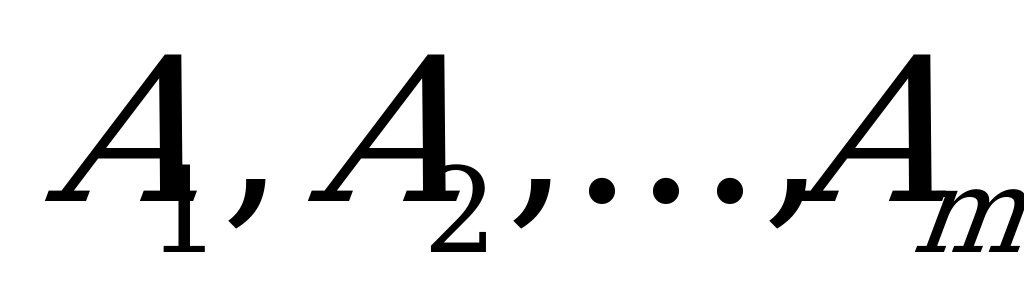
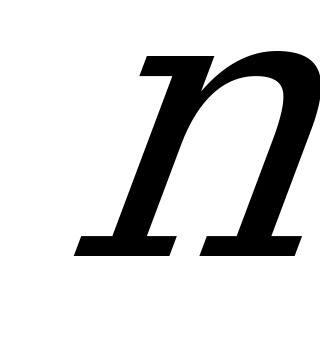
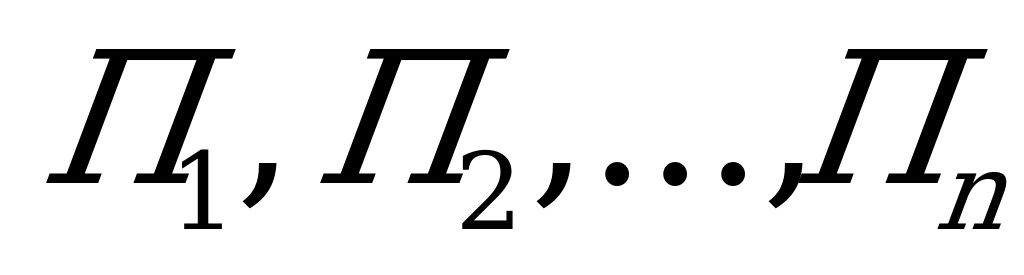
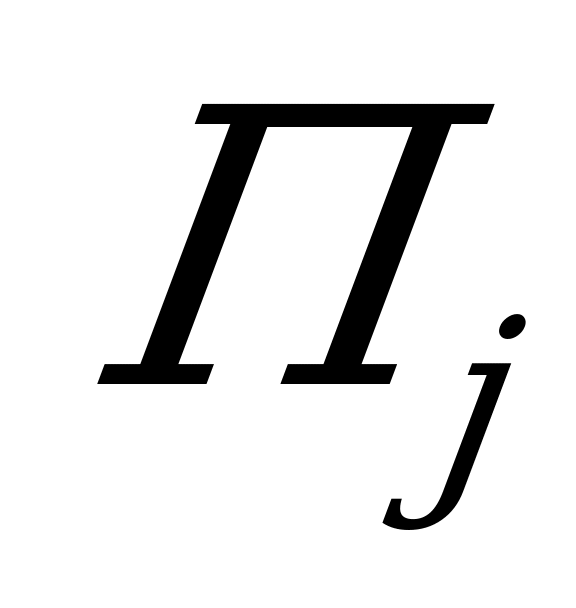
Рассмотрим игру с природой: у лица, принимающего решение (сторона ), имеется возможных стратегий ; что касается обстановки, то о ней можно сделать предположений . Рассмотрим их как «стратегии природы». Выигрыш при каждой паре стратегий , задаётся матрицей. Требуется выбрать такую стратегию игрока , которая является более выгодной по сравнению с другими.

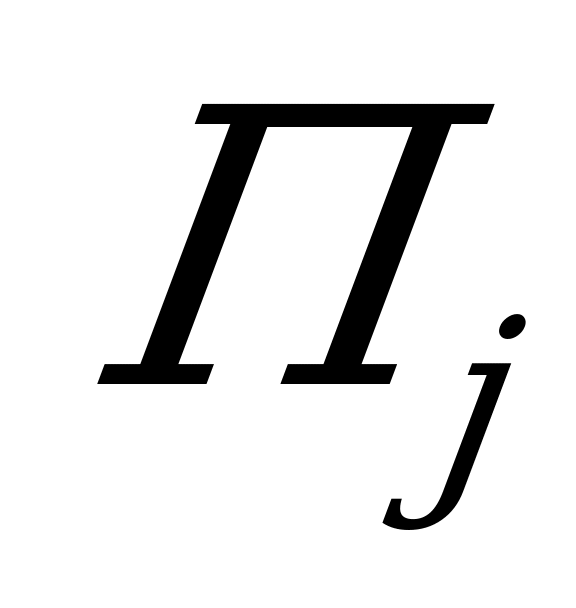
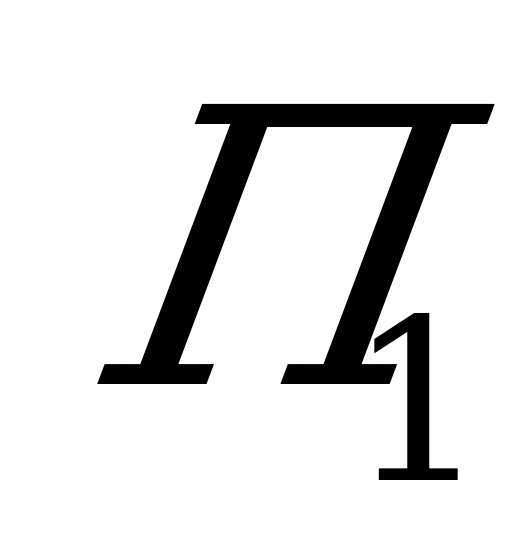
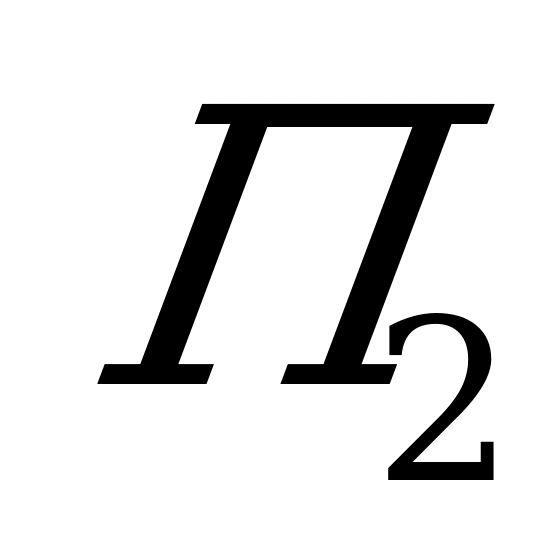
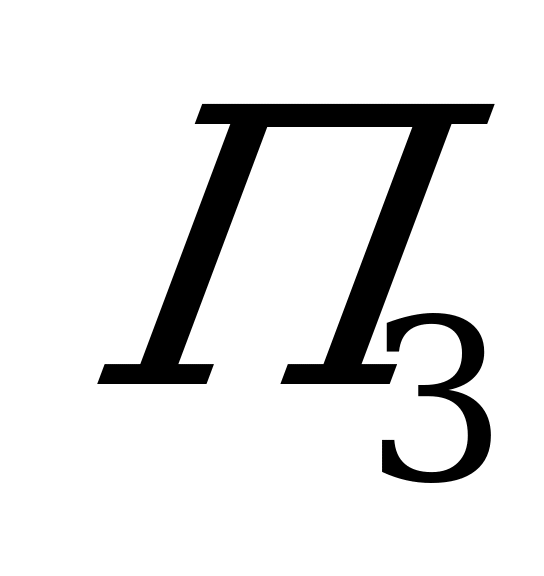
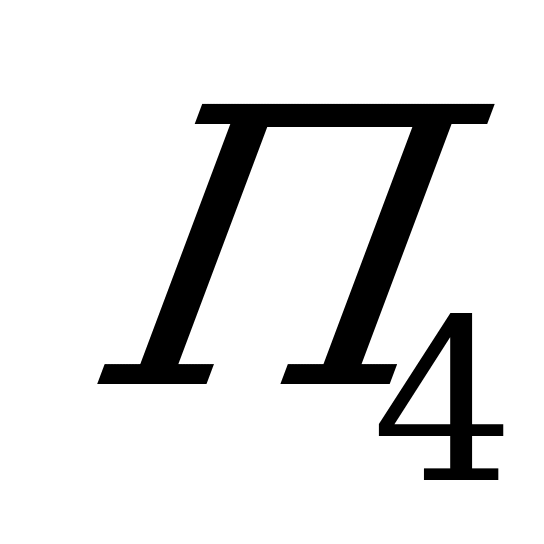
		1	2	3	5
		7	4	4	5
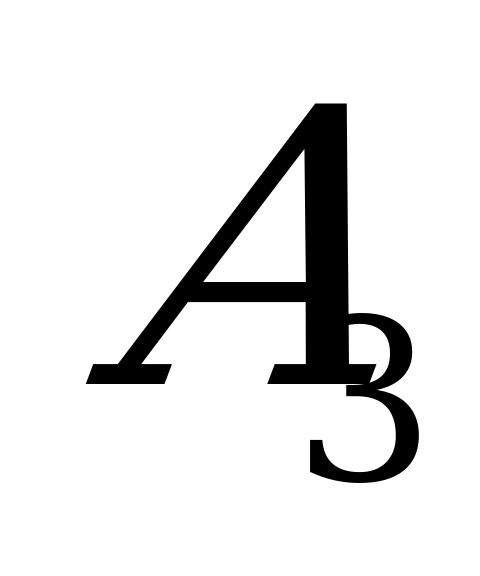
		3	4	4	1
		7	4	2	2

Самый простой случай выбора решения в игре с природой – это случай, когда какая-то из стратегий игрока превосходит другие (доминирует над ними), как, например, стратегия в следующей таблице. Здесь выигрыш при стратегии при любом состоянии природы не меньше, чем при других стратегиях, а при некоторых – больше; значит нужно выбирать именно эту стратегию.

Если даже в матрице игры с природой нет одной стратегии, доминирующей над всеми другими, всё же полезно посмотреть, нет ли в ней дублирующих стратегий и стратегий, уступающих другим при всех условиях. Однако мы можем уменьшить только число стратегий игрока . Стратегии природы нельзя опускать, поскольку она не имеет умысла навредить, более того, она может реализовать состояния, заведомо выгодные игроку .

Картина ситуации, которую даёт матрица выигрышей ( ), неполна и не отражает должным образом достоинств и недостатков каждого решения. Предположим, что выигрыш при стратегии и состоянии природы 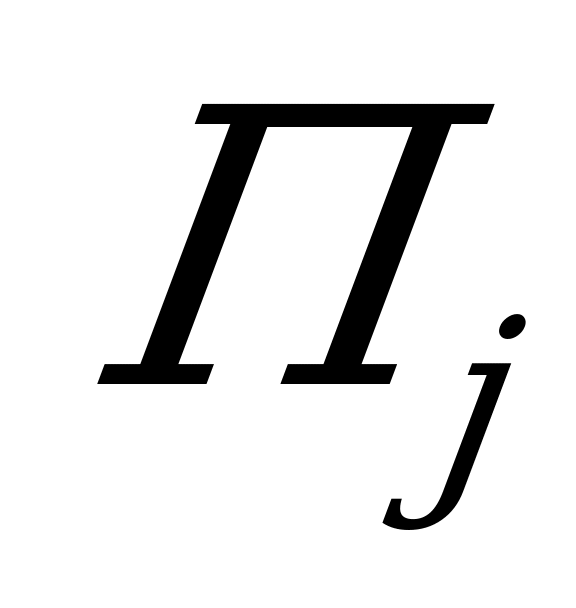больше, чем при стратегии 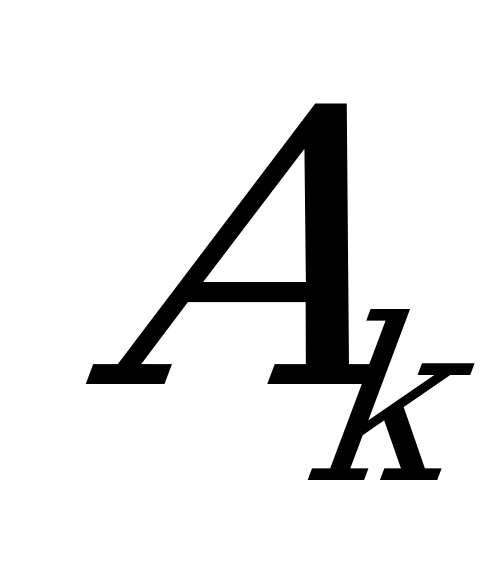и состоянии природы 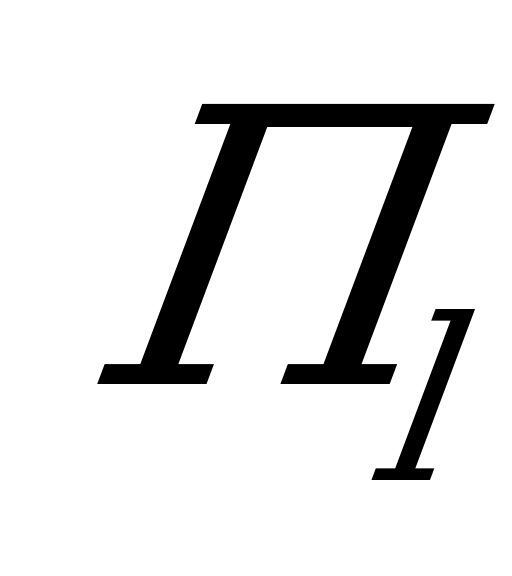: 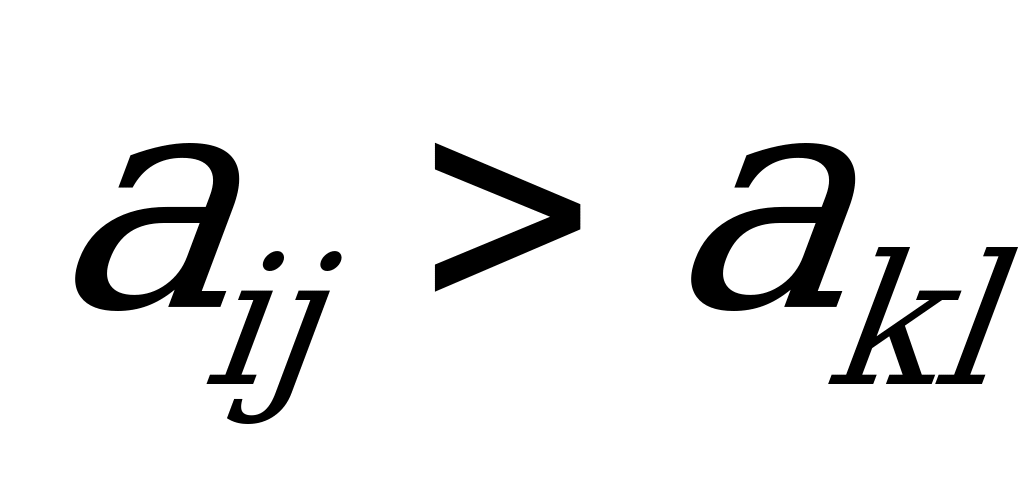. Но за счёт чего больше? За счёт того, что мы удачно выбрали стратегию ? Необязательно. Может быть, просто состояние природы 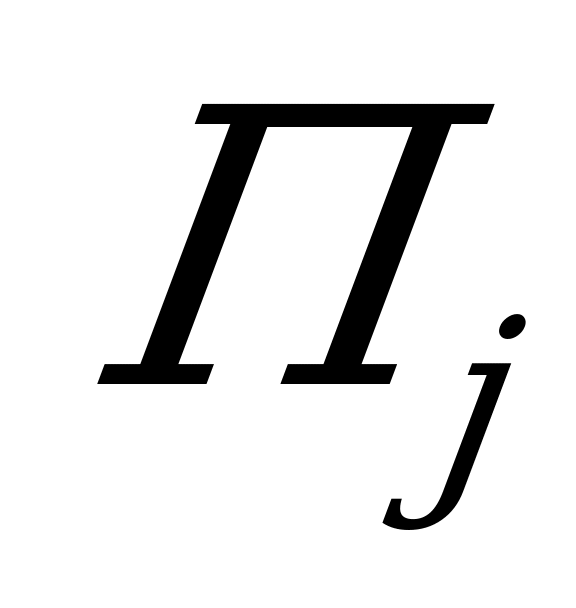выгоднее, чем 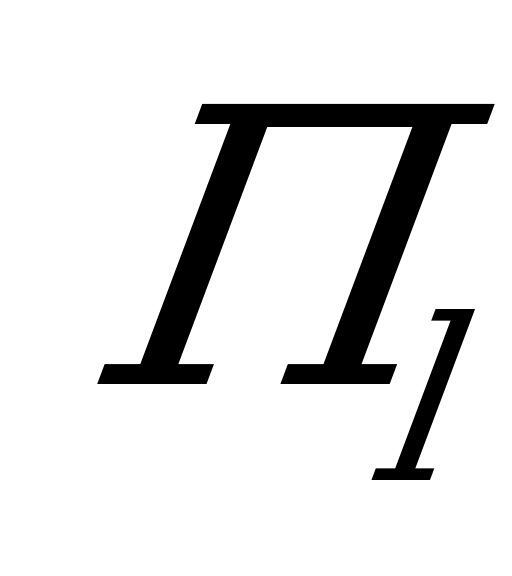. Например, состояние природы «нормальные условия» для любого мероприятия выгоднее, чем «наводнение», «землетрясение» и т.п. Желательно ввести такие показатели, которые не просто давали бы выигрыш при данной стратегии в каждой ситуации, но отражали бы «удачность» или «неудачность» выбора данной стратегии в данной ситуации.

С этой целью в теории решений вводится понятие риска (или «сожаления»).

Риском 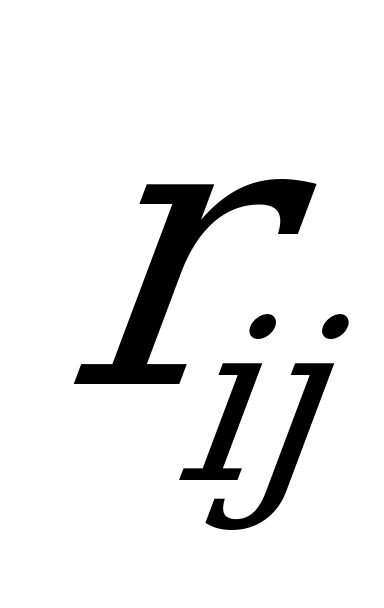игрока при пользовании стратегией в условиях 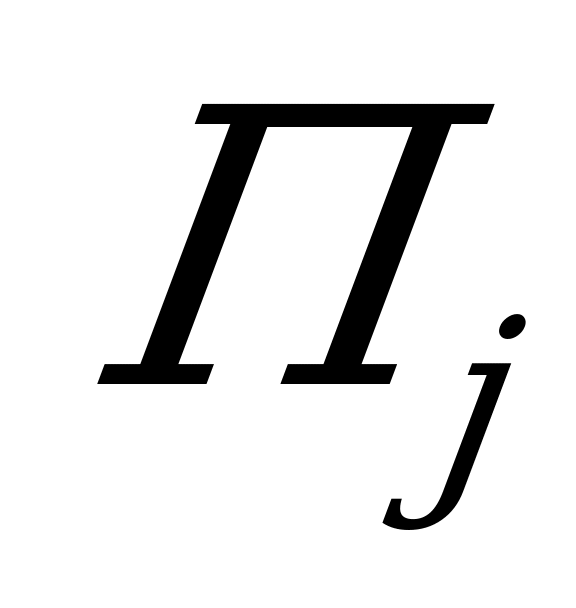называется разность между выигрышем, который мы получили бы, если бы знали условия 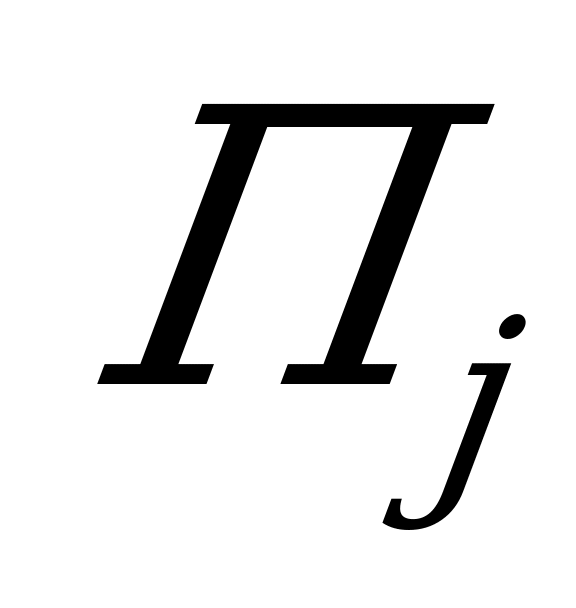, и выигрышем, который мы получим, не зная их и выбирая стратегию .

Очевидно, если бы игрок знал состояние природы 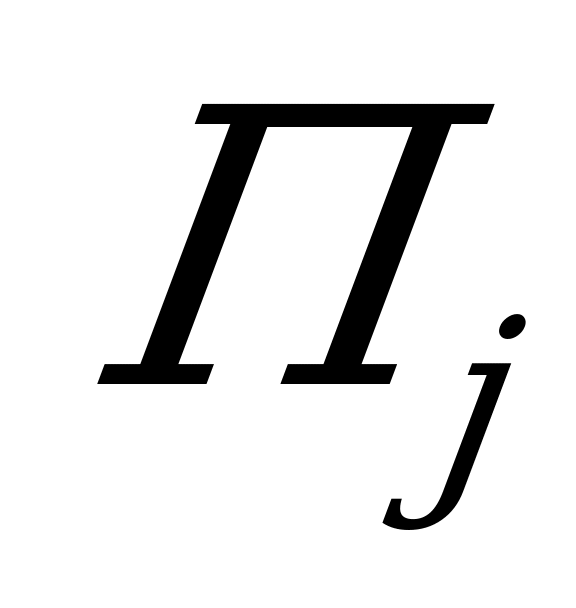, он выбрал бы ту стратегию, при которой его выигрыш максимален. Этот выигрыш, максимальный в столбце 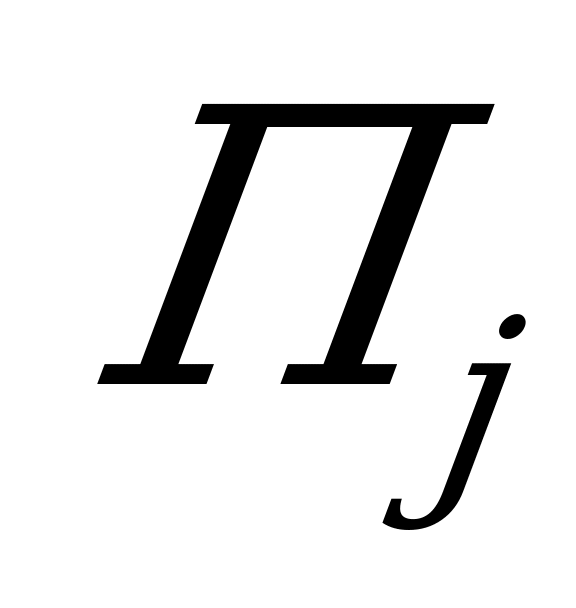, обозначим 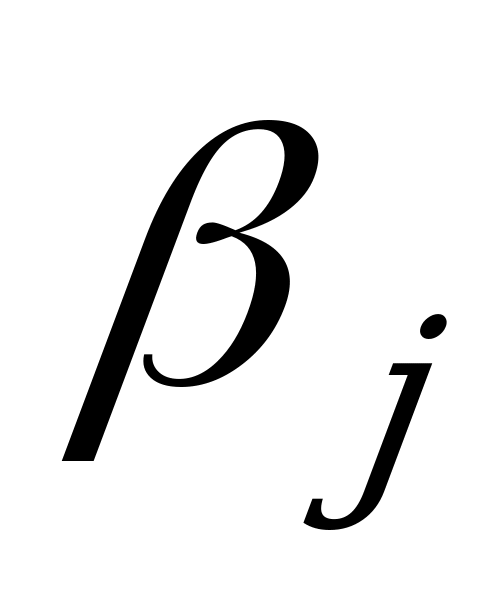. Чтобы получить риск 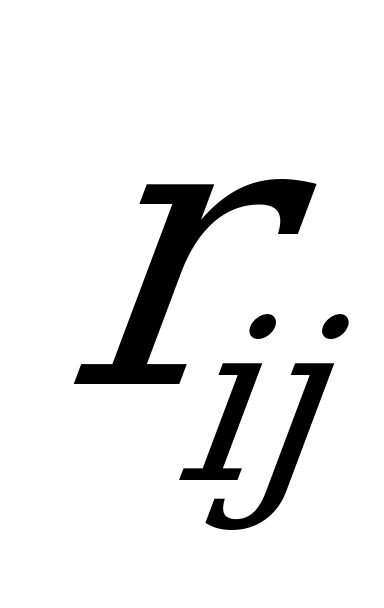, нужно из 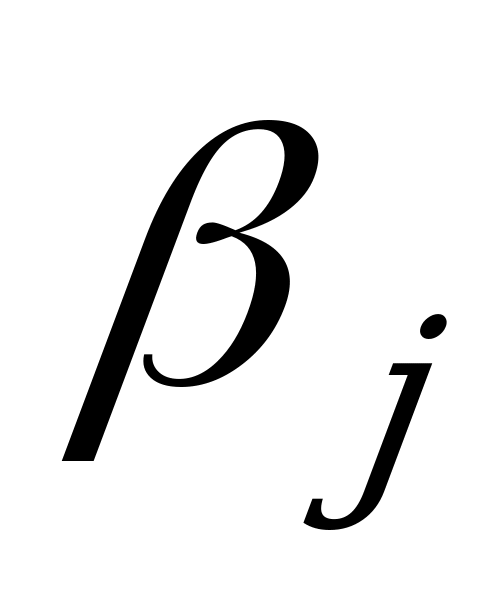вычесть фактический выигрыш :

.

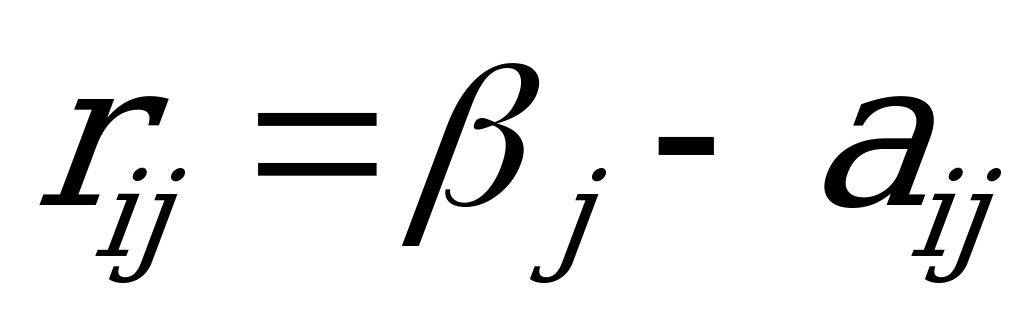Матрица рисков
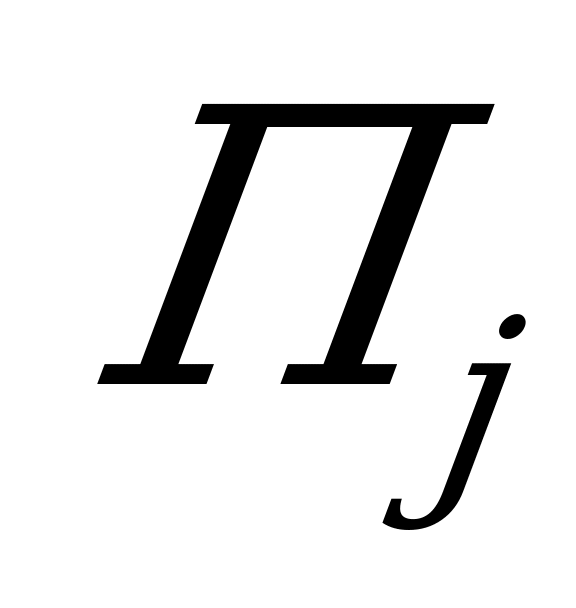
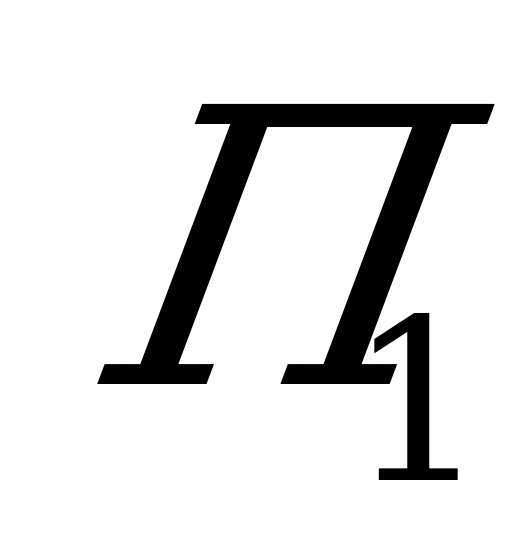
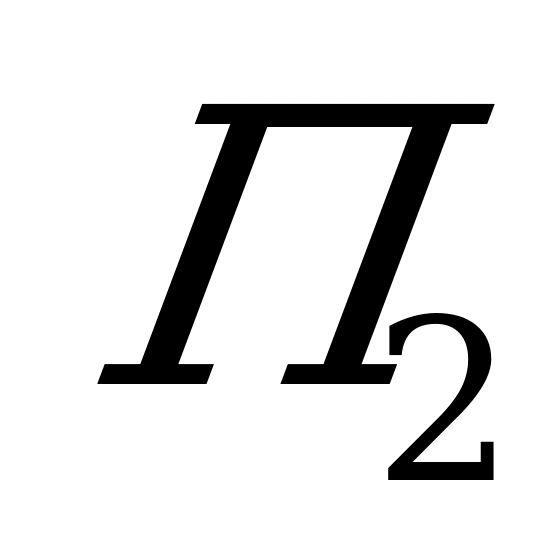
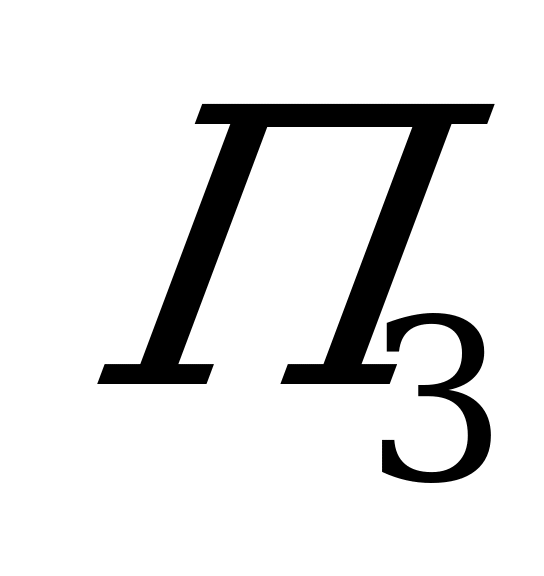
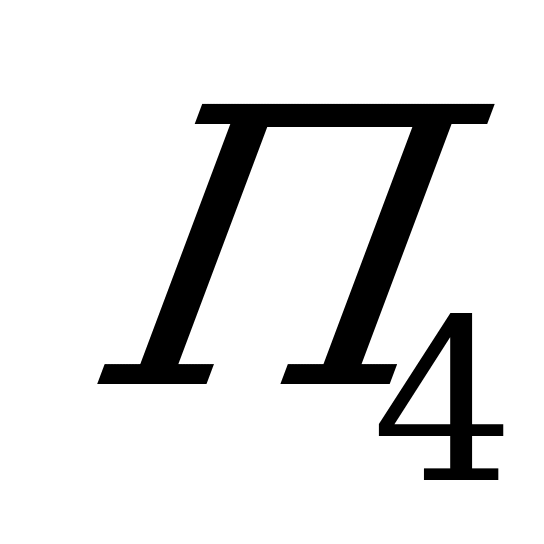
		3	4	1	0
		1	0	2	6
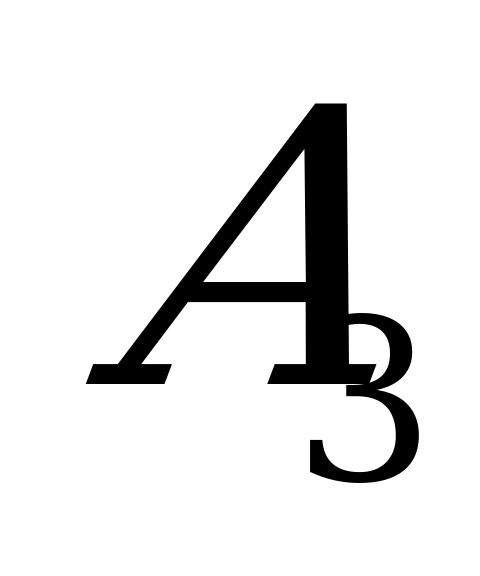
		0	2	0	7

Пример 1. Дана матрица выигрышей ( ). Требуется построить для неё матрицу рисков ( ).

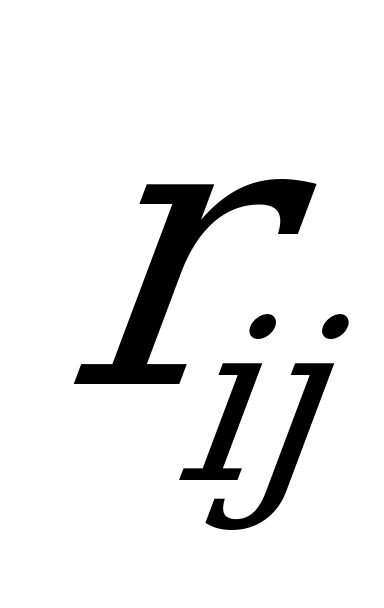
Матрица выигрышей
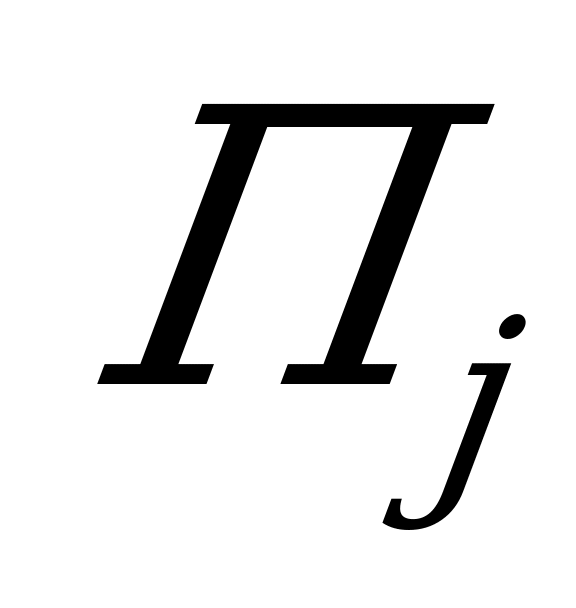
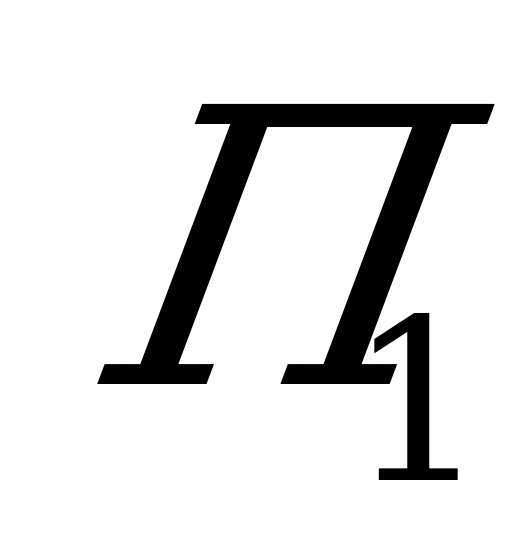
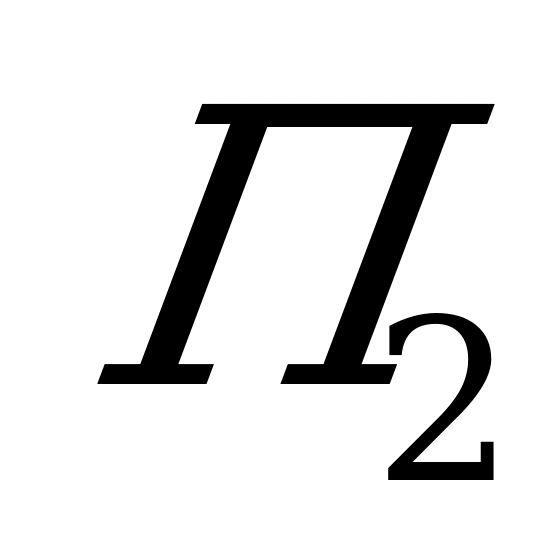
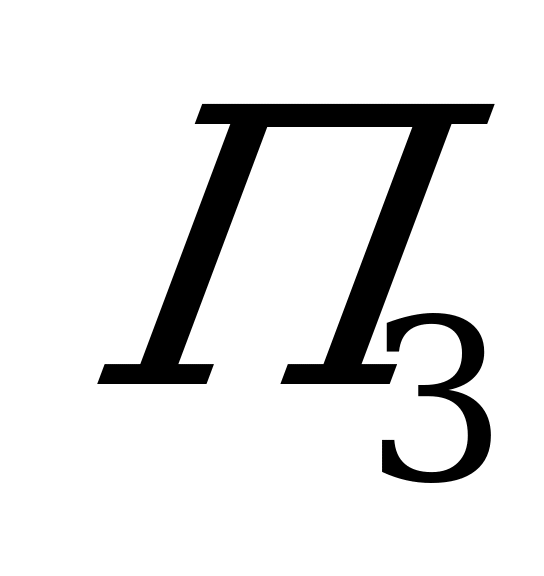
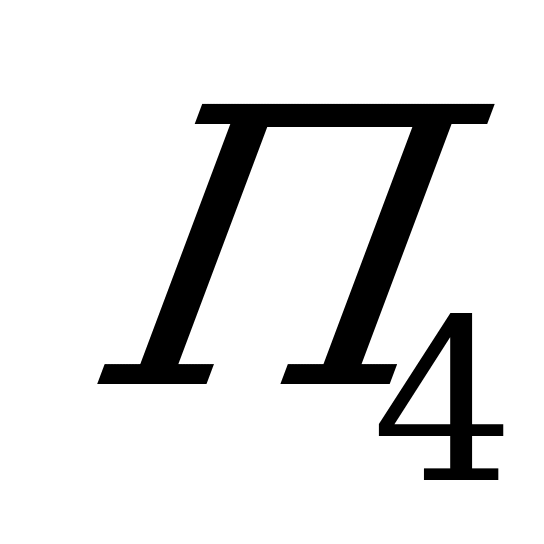
		1	4	5	9
		3	8	4	3
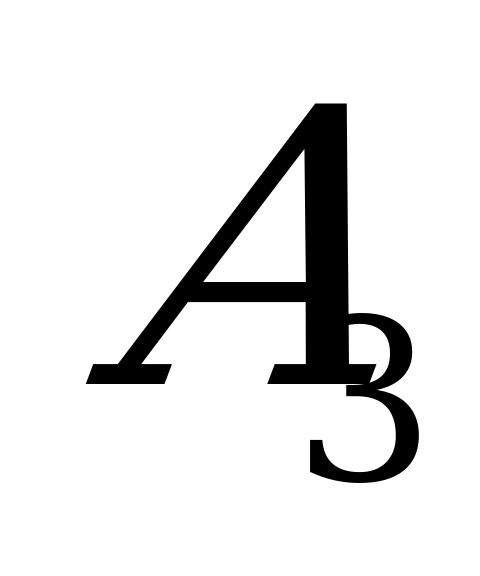
		4	6	6	2
		4	8	6	9

При взгляде на матрицу рисков становятся яснее некоторые черты данной игры с природой. Так, в матрице выигрышей ( ) во второй строке первый и последний элементы равны друг другу: 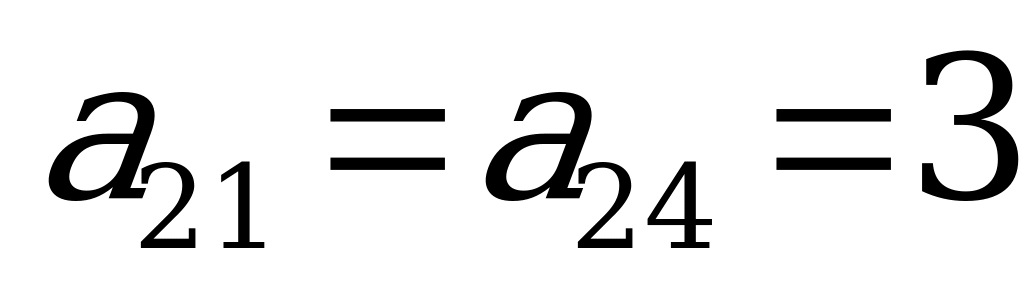. Однако эти выигрыши совсем не равноценны в смысле удачного выбора стратегии: при состоянии природы 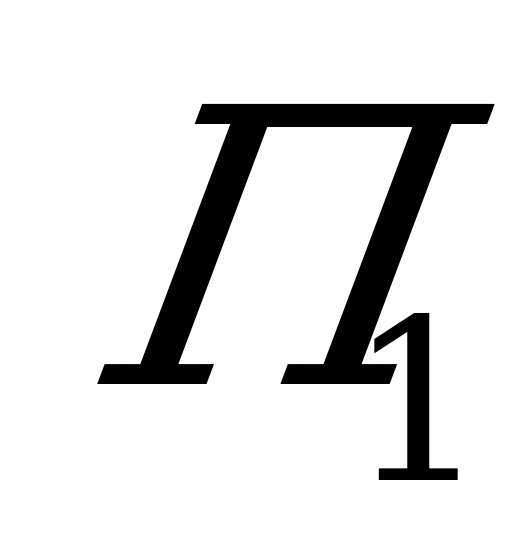мы могли выиграть самое большее 4, и наш выбор стратегии почти совершенно хорош; а вот при состоянии 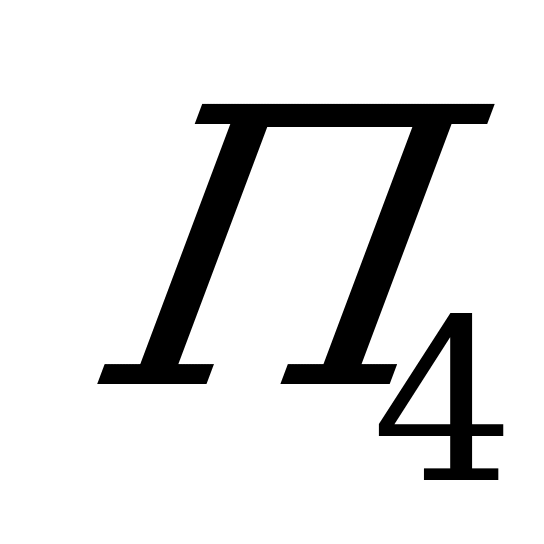мы могли бы, выбрав стратегию , получить на целых 6 единиц больше, т.е. выбор стратегии очень плох.

Риск (сожаление) – это «плата» за отсутствие информации. Естественно, нам хотелось бы минимизировать риск, сопровождающий выбор решения.

Оптимальную стратегию игрока можно определить, используя ряд критериев.

1. Критерий Байеса.

Этот критерий применяется при известном распределении вероятностей состояний природы 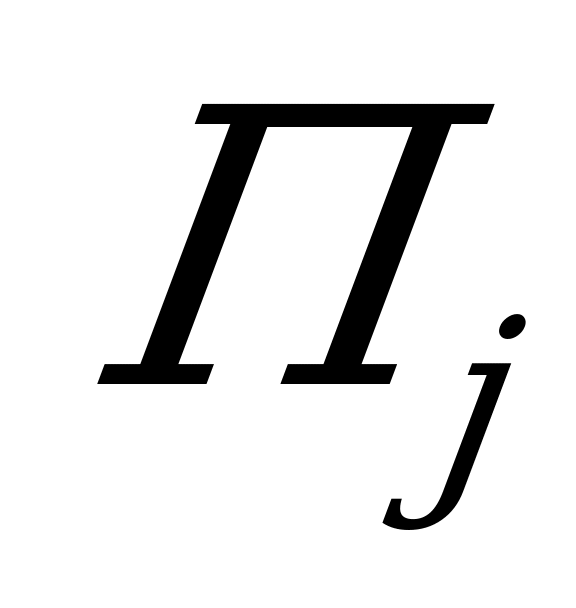: 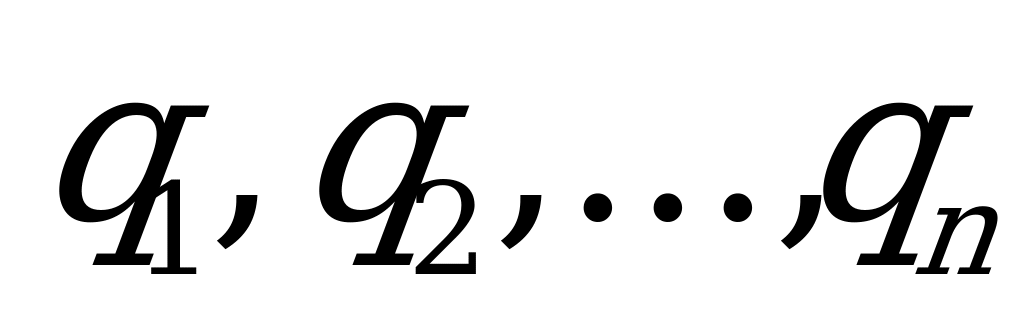. В этом случае выбирается та стратегия, для которой среднее значение выигрыша (математическое ожидание выигрыша) максимально. Та же стратегия, которая обращает в максимум средний выигрыш, обращает в минимум средний риск. Поэтому в случае стохастической неопределённости оба подхода дают одно и то же оптимальное решение.

Пример 2.1. Планируется построить предприятие по производству некоторой продукции. Неопределённость спроса 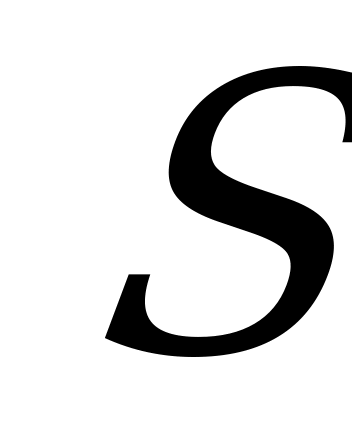на продукцию приводит к тому, что предприятие теряет возможный доход, если объём выпускаемой продукции 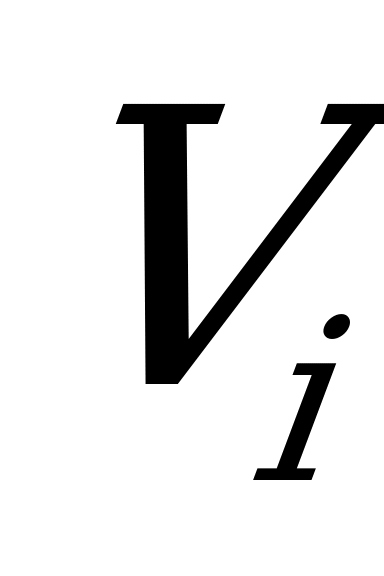меньше уровня спроса , и несёт убытки (связанные с хранением и утилизацией), если объём продукции превышает уровень спроса. Предположим, что спрос на продукцию выражается величинами 10, 20, 30, 40 тыс.ед. Планирующий орган предприятия может принять одно из следующих решений: построить предприятие мощностью 10, 20, 30, 40 тыс.ед. продукции. Доход от реализации единицы продукции составляет 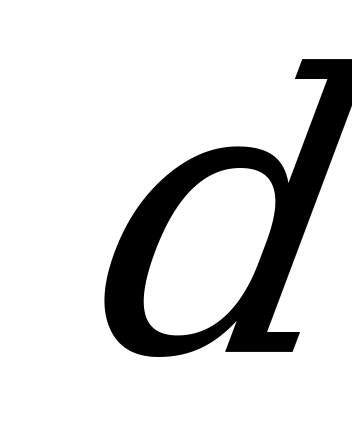=15 ден.ед., а издержки от нереализованной единицы продукции – 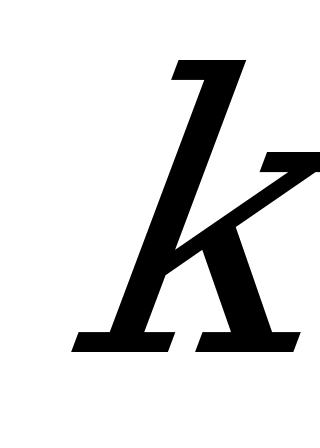=5 ден.ед. Известны вероятности спроса на данную продукцию: 0,3; 0,2; 0,4; 0,1.

Требуется дать обоснованные рекомендации по строительству предприятия необходимой мощности.

Решение. Игроком (или лицом, принимающим решение) выступает планирующий орган предприятия. Второй стороной – природой – будем считать совокупность объективных внешних условий, из которых формируется спрос потребителей. Составим платёжную матрицу.

Стратегии игрока (мощность предприятия, тыс.ед)	Спрос потребителей, тыс.ед.
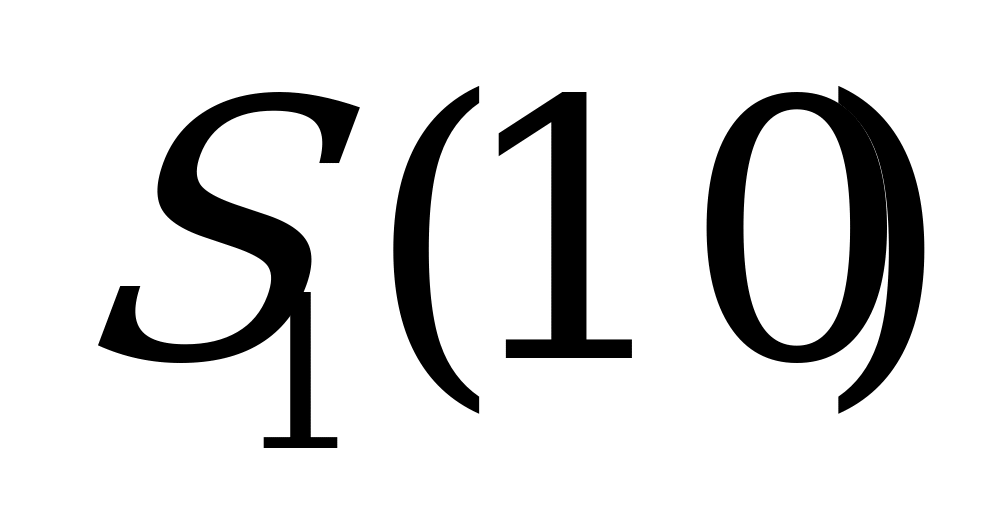
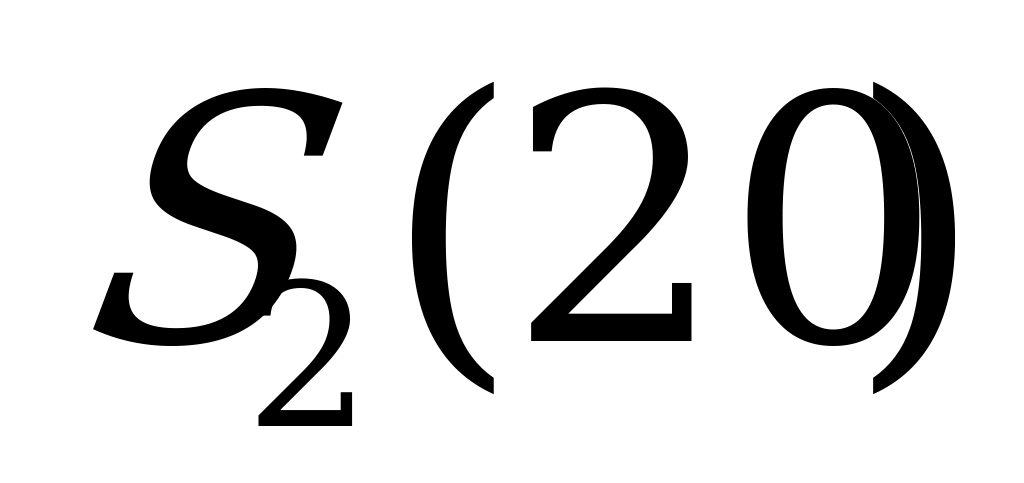
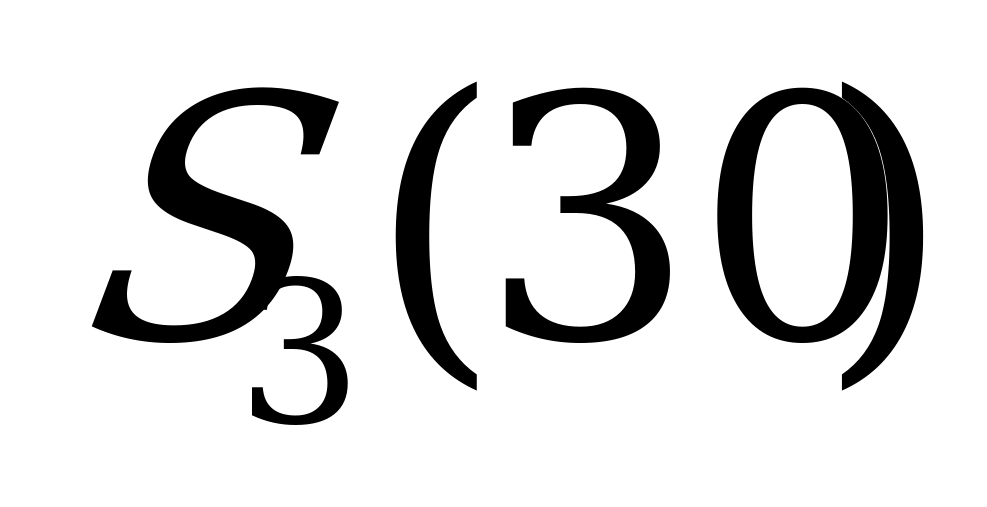
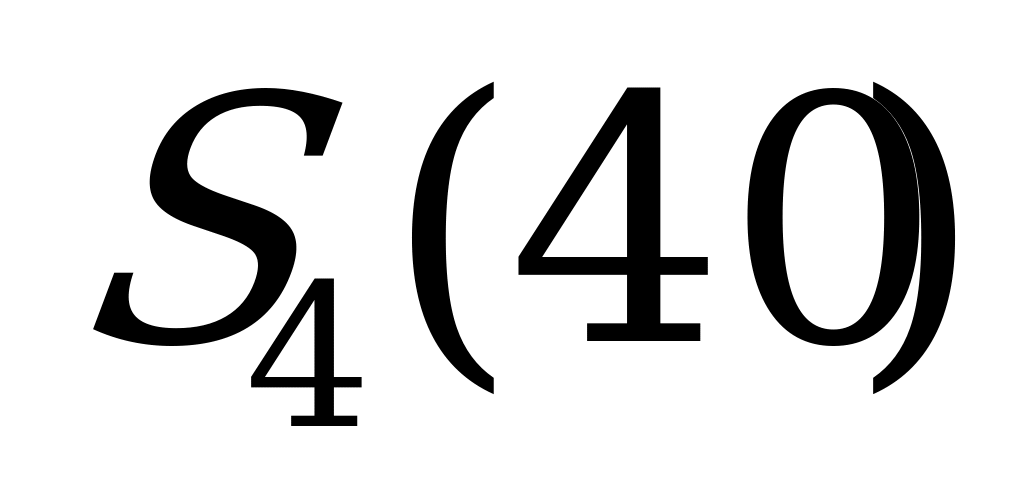
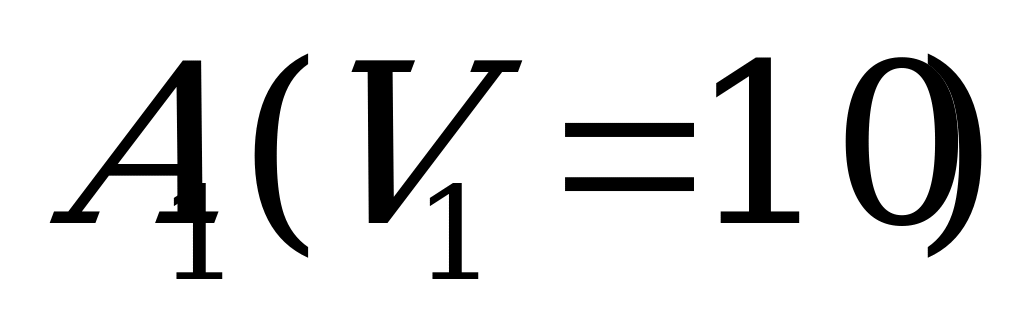
	150	150	150	150
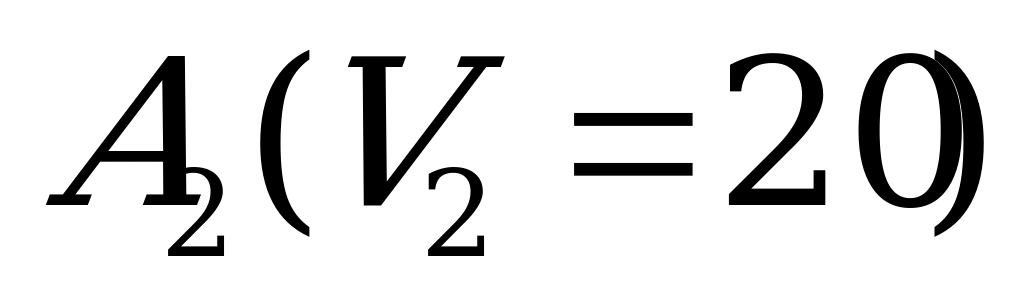
	100	300	300	300
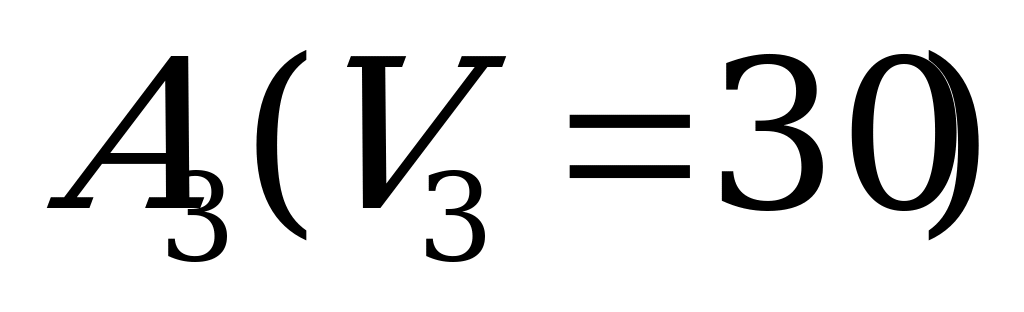
	50	250	450	450
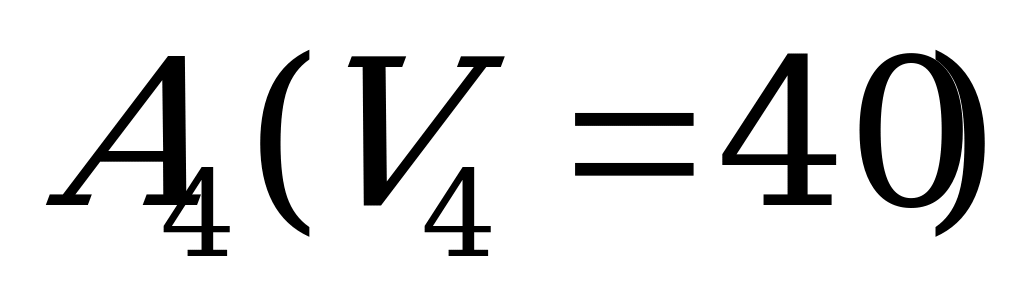
	0	200	400	600
	0,3	0,2	0,4	0,1

Функцию платежей (выигрышей) можно записать в виде кусочно-линейной функции:

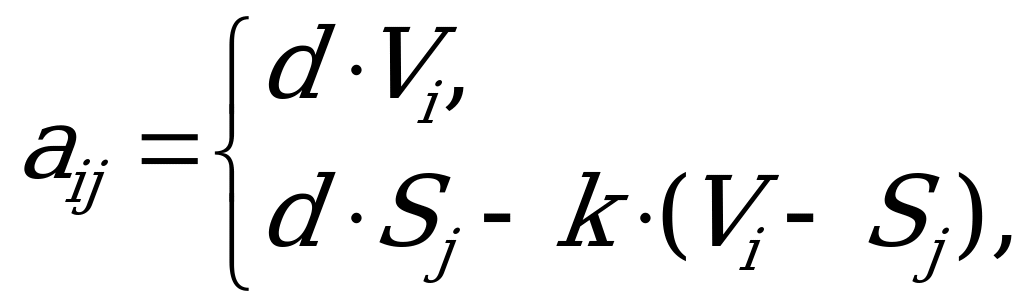
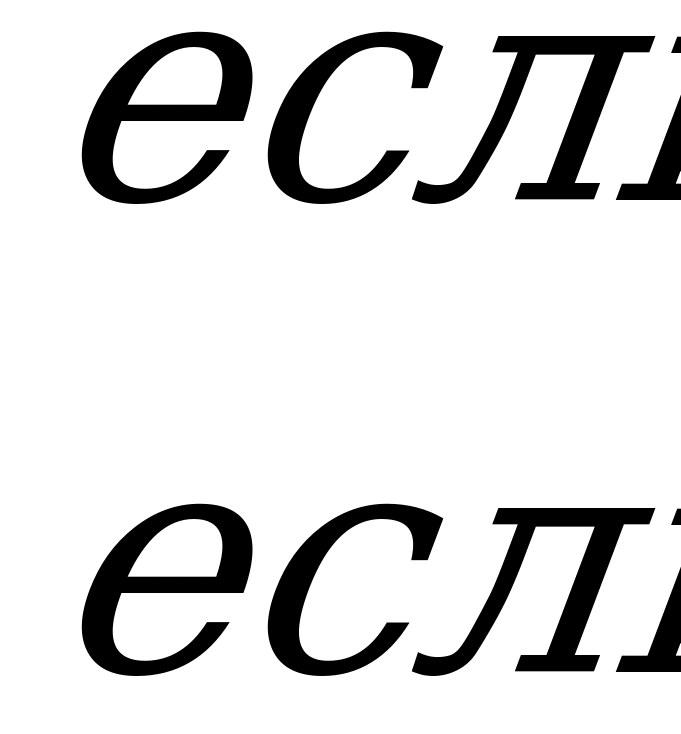
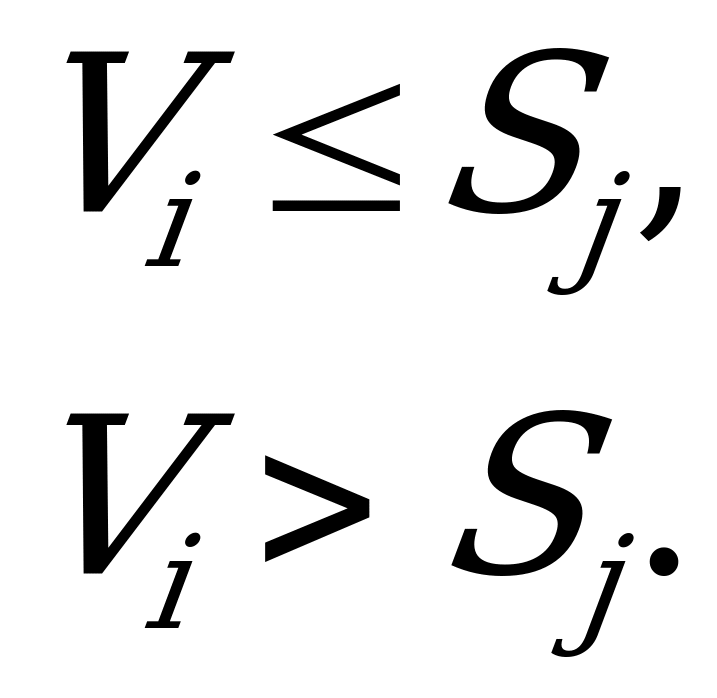
Вычисляем средние выигрыши :

, ,

, .

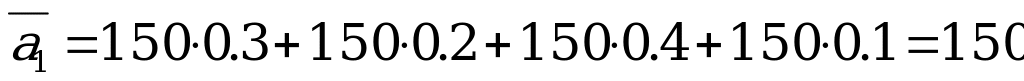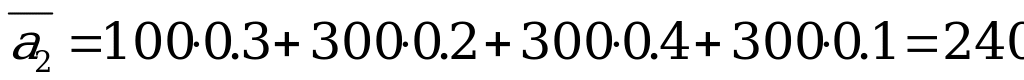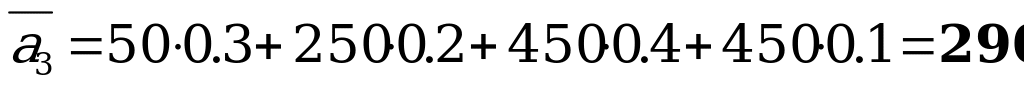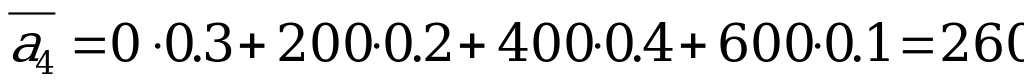Оптимальной стратегией по Байесу является , поскольку ей соответствует максимальная средняя прибыль.

1. Принцип недостаточного основания Лапласа.

Этот принцип применяется, когда вероятности состояний природы неизвестны. Согласно принципу Лапласа все состояния природы полагаются равновероятными, т.е.

.

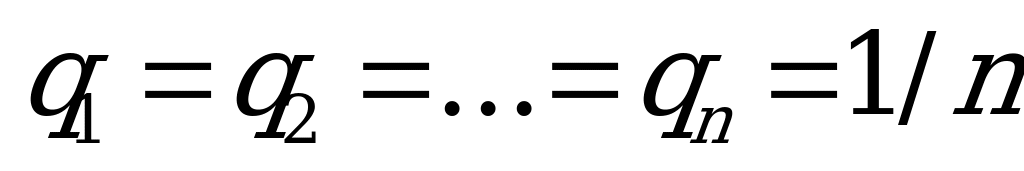Оптимальной считается стратегия, обеспечивающая максимум среднего выигрыша.

Стратегии игрока (мощность предприятия, тыс.ед)	Спрос потребителей, тыс.ед.
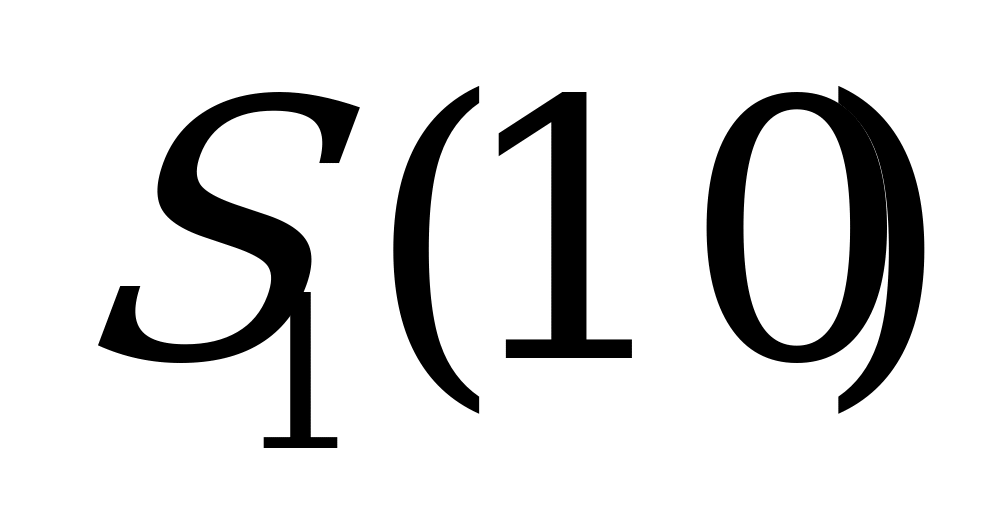
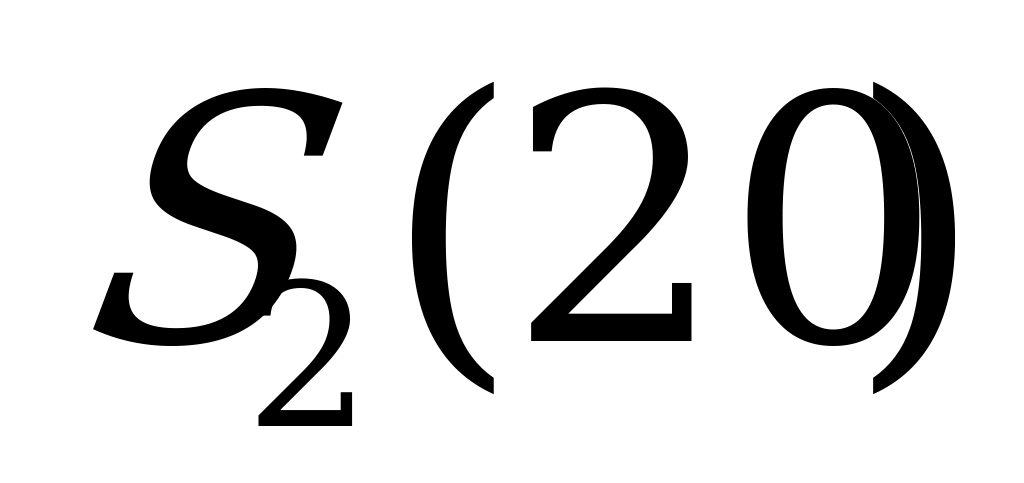
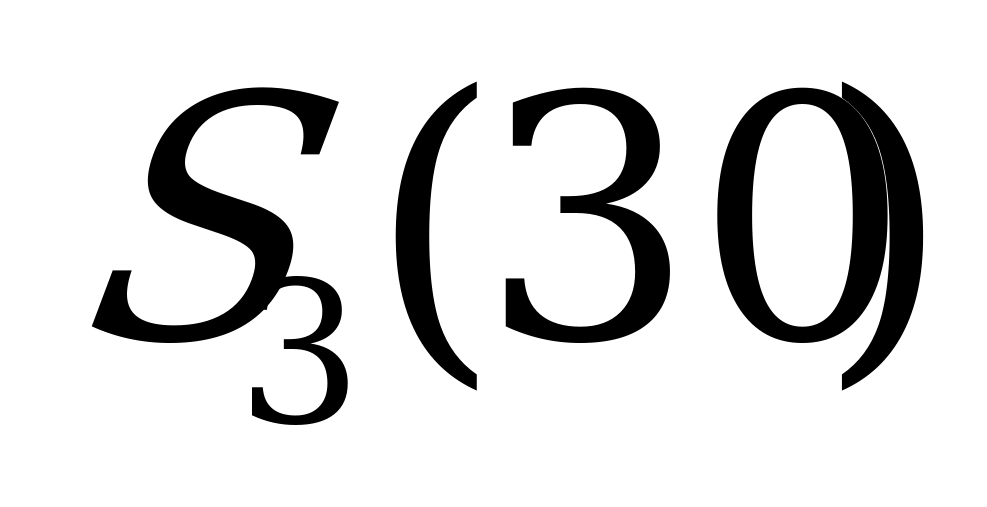
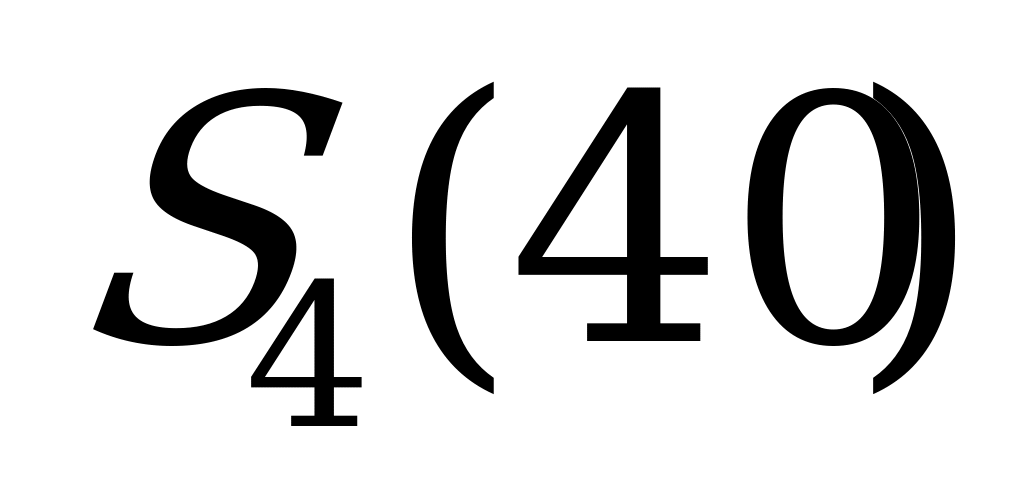
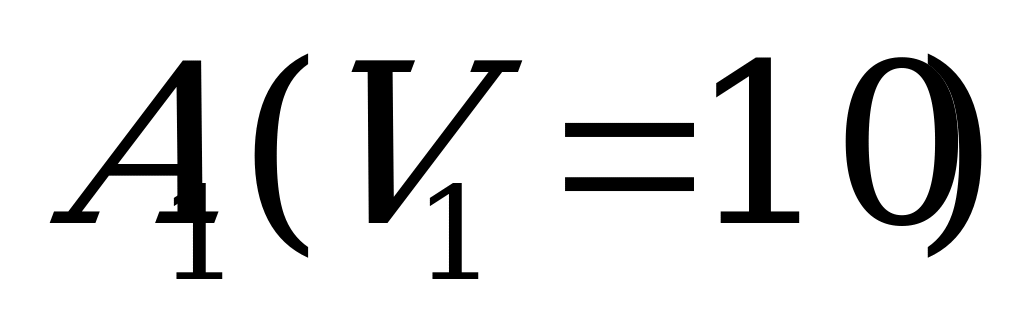
	150	150	150	150
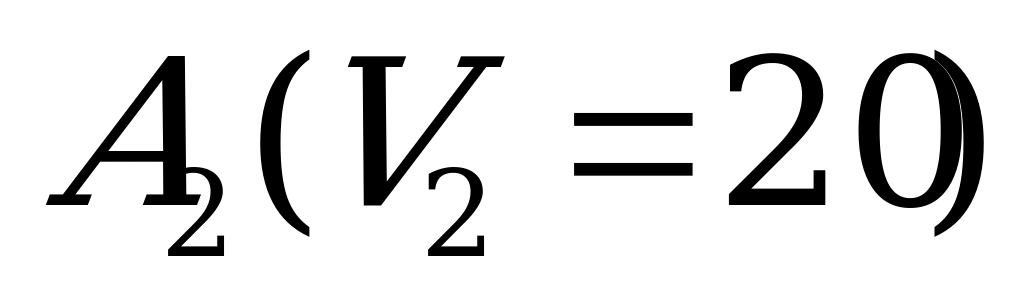
	100	300	300	300
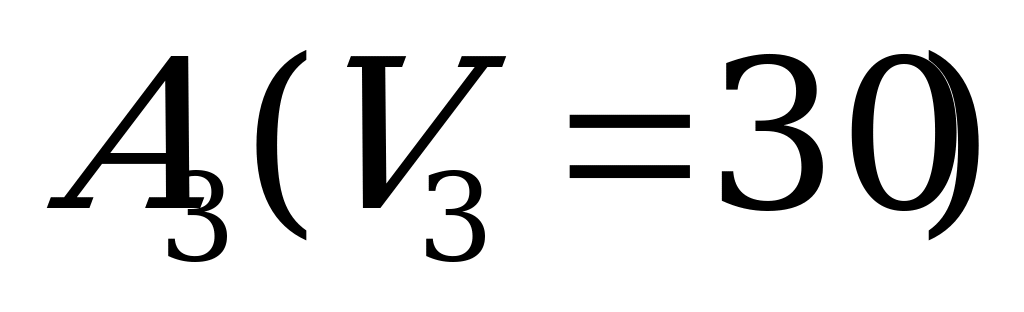
	50	250	450	450
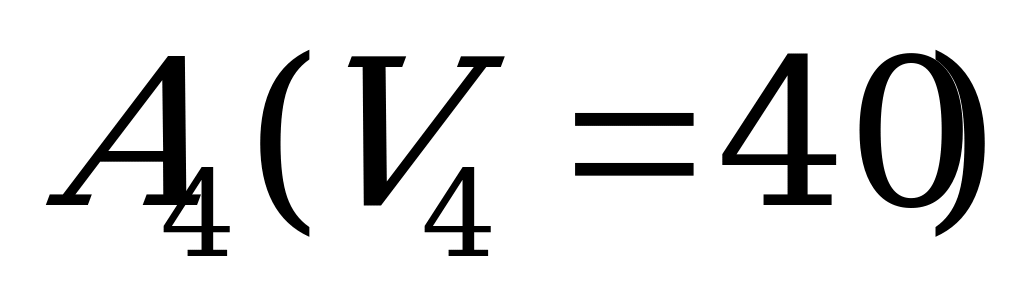
	0	200	400	600

Пример 2.2. Найти оптимальную стратегию, пользуясь критерием Лапласа.

Решение.

По критерию Лапласа ;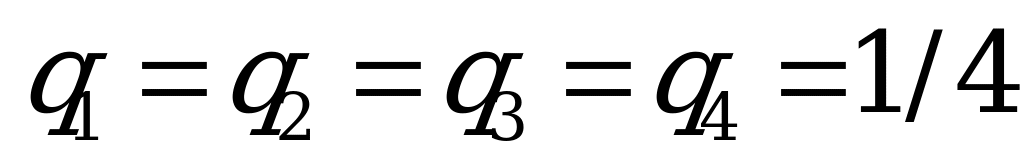

средние выигрыши равны: ,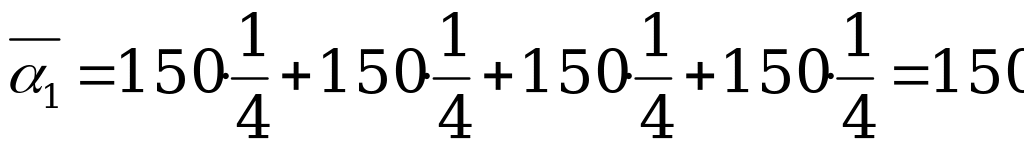

,

,

.

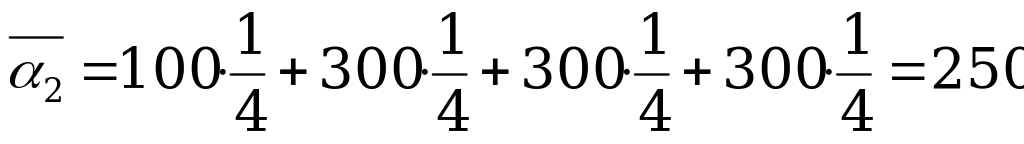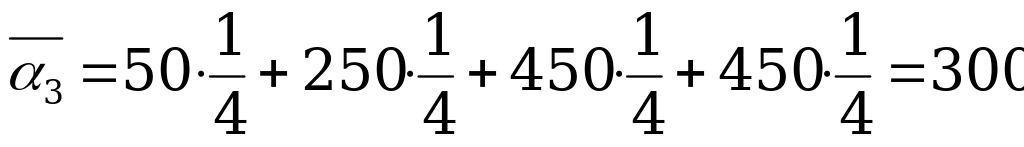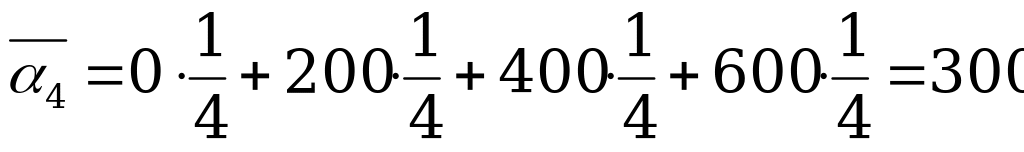Оптимальными стратегиями по Лапласу являются и , т.к. им соответствует максимальная прибыль, равная 300 тыс. ден.ед.

Если вопрос распределения вероятностей состояний природы не решён, то используют следующие критерии.

1. Максиминный критерий Вальда.

По этому критерию за оптимальную принимается та стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е.

.

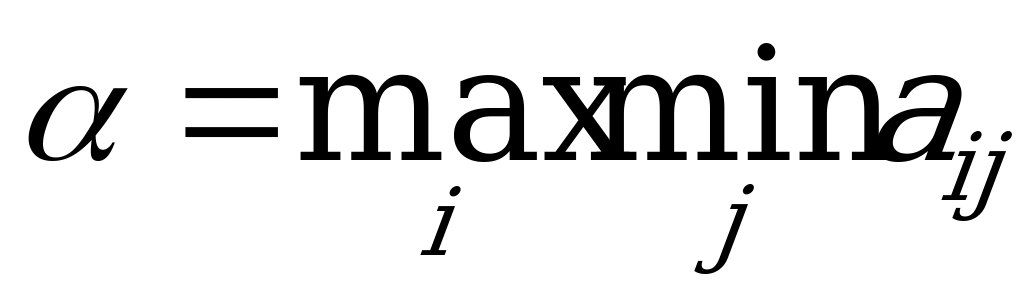Этот критерий олицетворяет «позицию крайнего пессимизма». Очевидно, такой подход – перестраховочный, естественный для того, кто очень боится проиграть.

Пример 2.3. В рассматриваемой задаче найти оптимальную стратегию, пользуясь критерием Вальда.

Решение. По критерию Вальда оптимальной является стратегия :

.

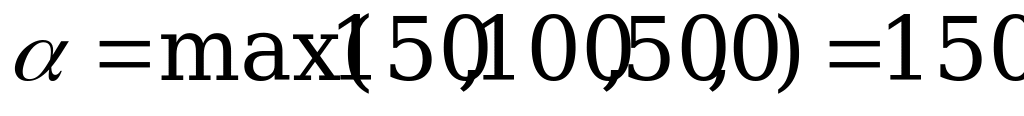1. Критерий минимального риска (критерий Сэвиджа).

Этот критерий – тоже крайне пессимистический, но при выборе оптимальной стратегии советует ориентироваться не на выигрыш, а на риск. Выбирается в качестве оптимальной та стратегия, при которой величина риска в наихудших условиях минимальна, т.е.

.

Сущность такого подхода в том, чтобы всячески избегать большого риска при принятии решения.

Пример 2.4.

Стратегии игрока (мощность предприятия, тыс.ед)	Спрос потребителей, тыс.ед.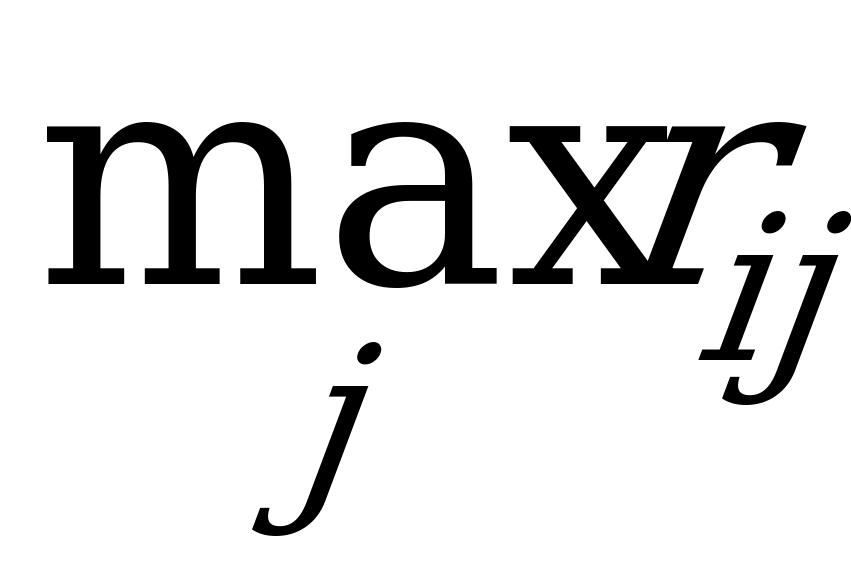
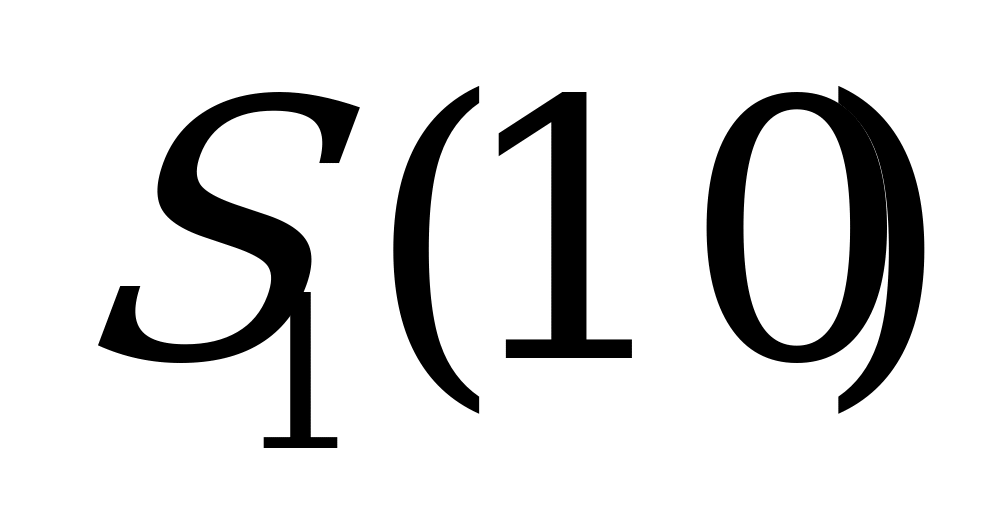
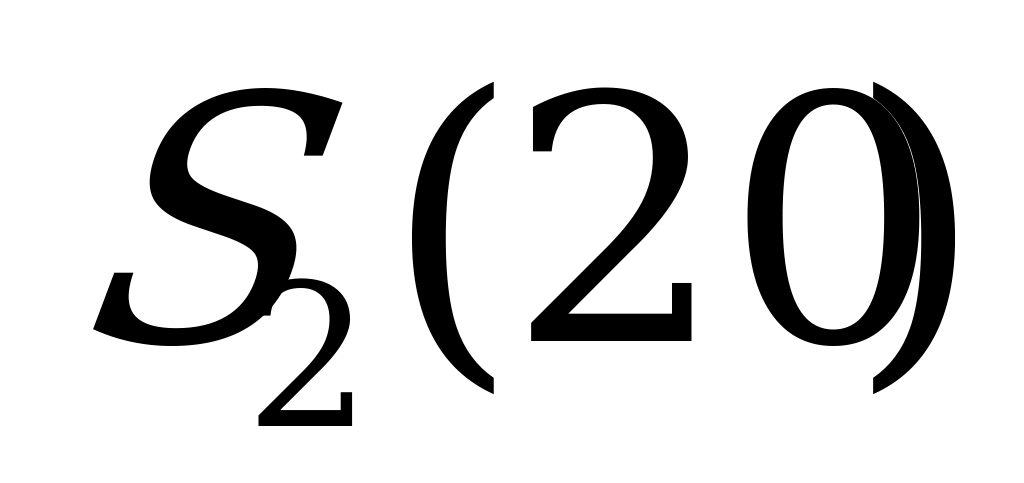
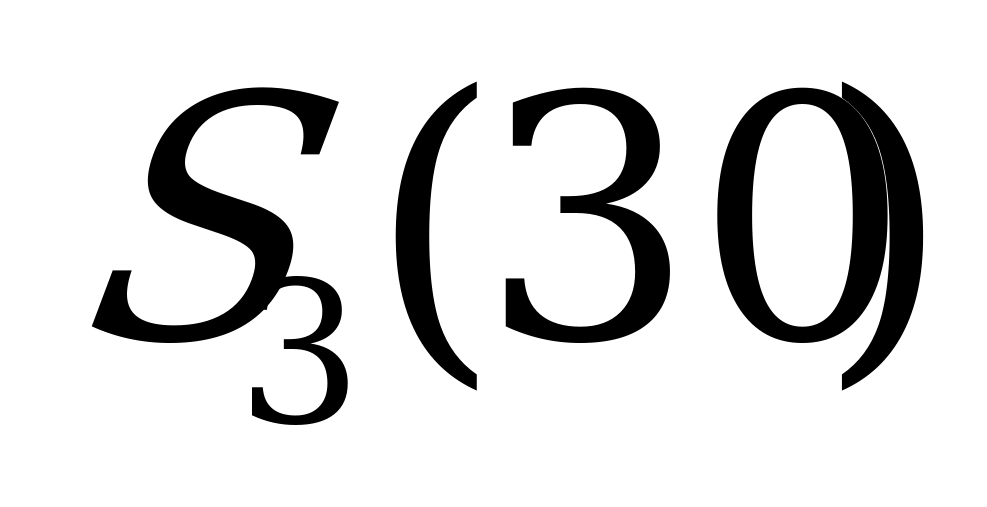
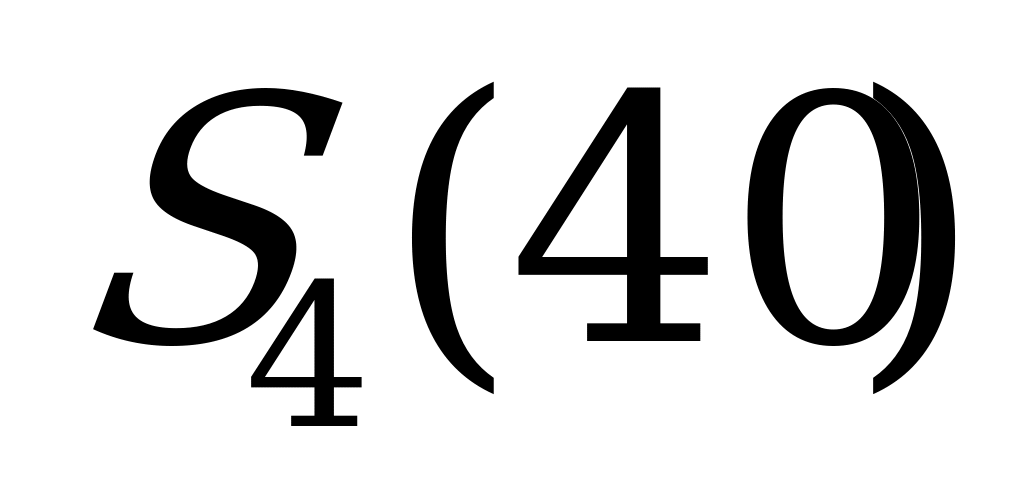
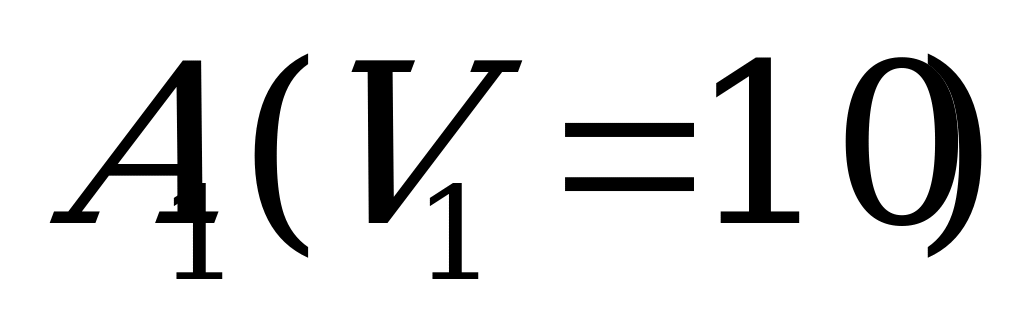
	0	150	300	450	450
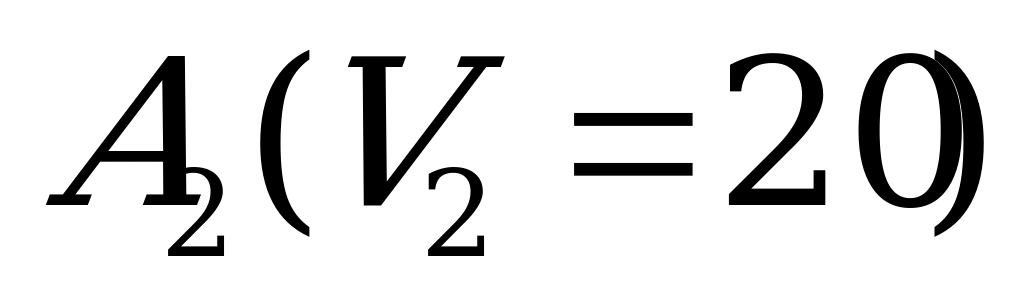
	50	0	150	300	300
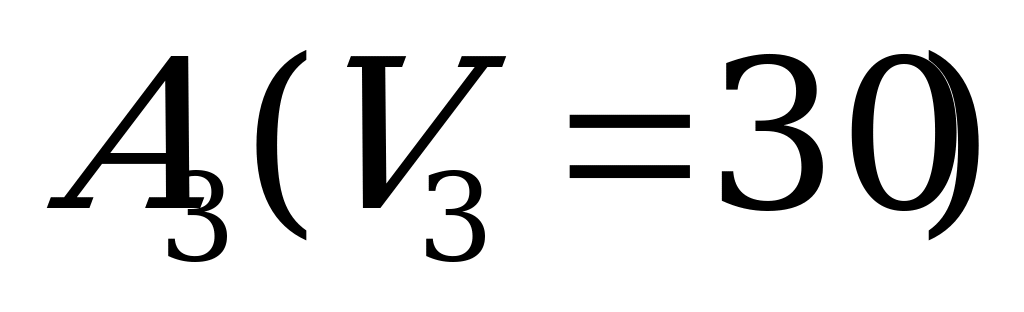
	100	50	0	150	150
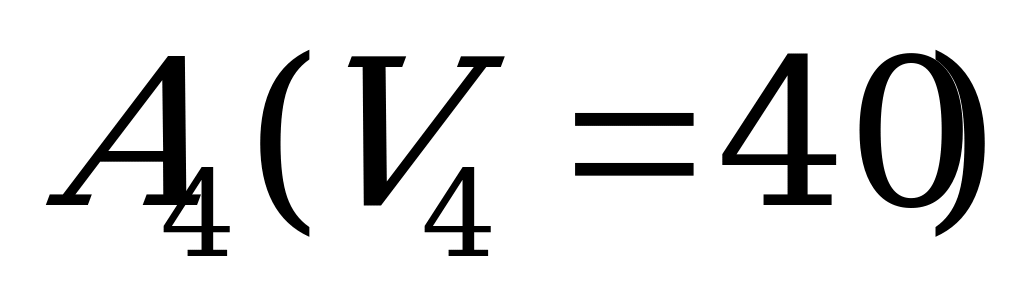
	150	100	50	0	150

Построим матрицу рисков.

Решение. По критерию Сэвиджа оптимальными являются стратегии и , для которых в наихудших условиях величина риска 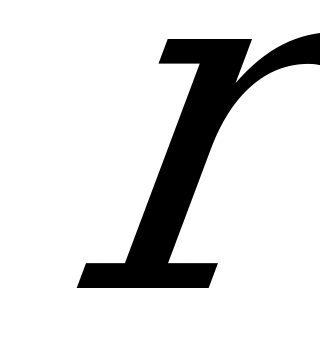принимает наименьшее значение, равное 150 тыс. ден.ед:

.

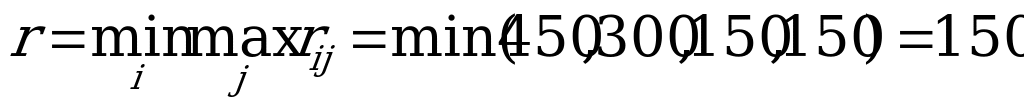1. Критерий пессимизма-оптимизма (критерий Гурвица).

За оптимальную принимается та стратегия, для которой выполняется соотношение

,

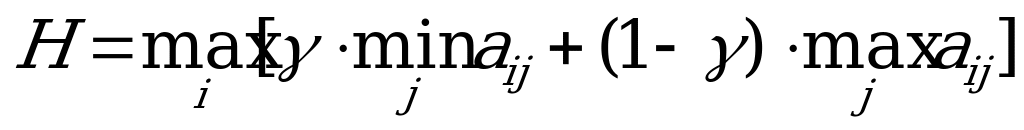где 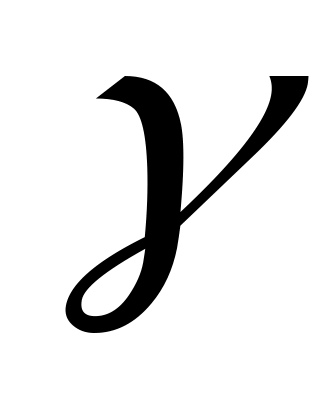- коэффициент пессимизма, выбираемый между 0 и 1.

При 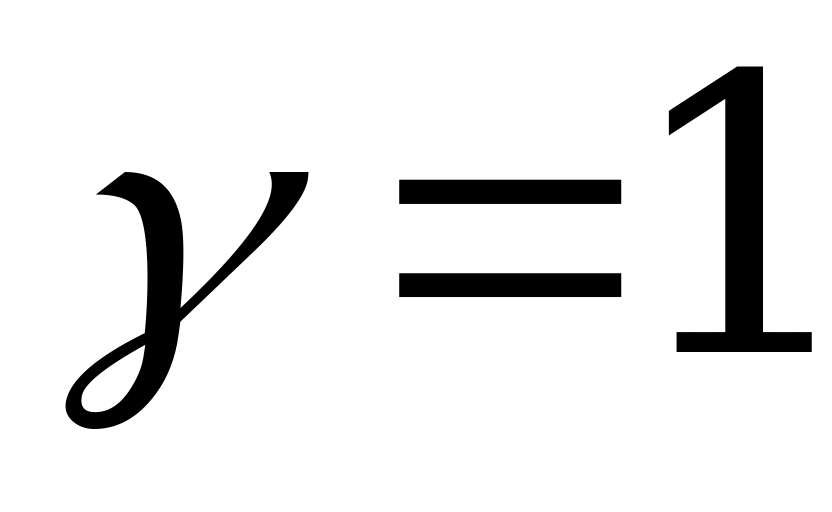критерий Гурвица превращается в критерий Вальда; при 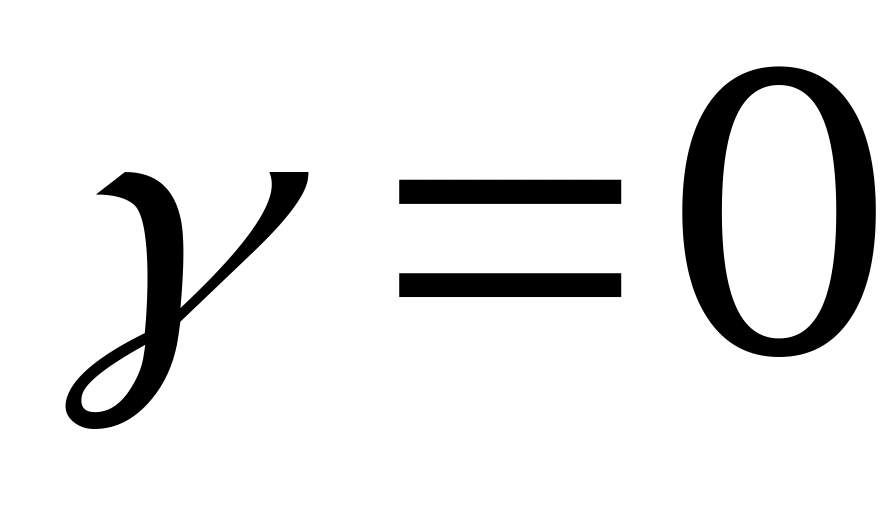- в критерий «крайнего оптимизма», рекомендующий выбрать ту стратегию, при которой самый большой выигрыш в строке максимален. При 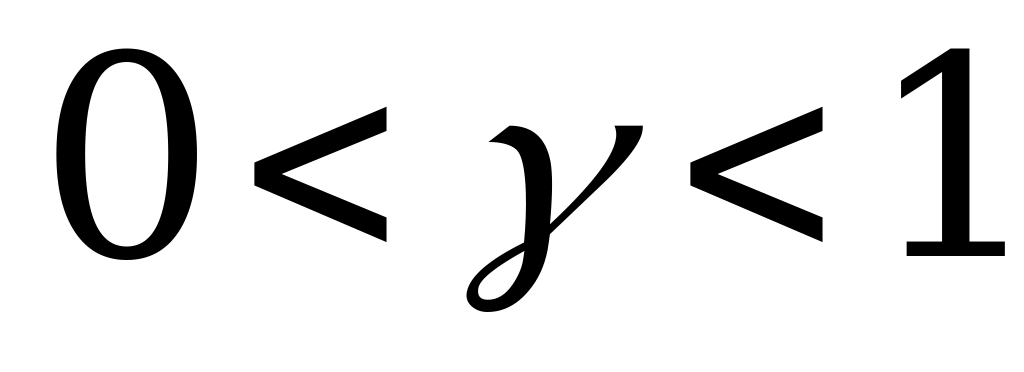получается нечто среднее между тем и другим. Коэффициент 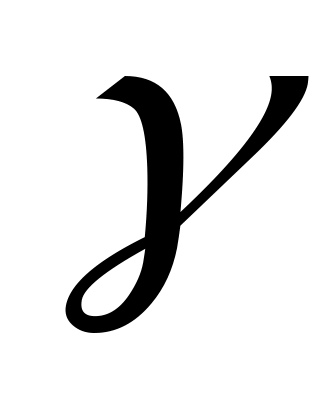выбирается из субъективных соображений: чем опаснее ситуация, чем больше мы хотим в ней подстраховаться, чем меньше наша склонность к риску, тем ближе к 1 выбирается .

При желании можно построить критерий, аналогичный , исходя не из выигрыша, а из риска.

Если рекомендации, вытекающие из различных критериев, совпадают, значит можно смело выбрать рекомендуемое решение. Если же (как это часто бывает) рекомендации противоречат друг другу, следует задуматься над этими рекомендациями и выяснить, насколько к разным результатам они приводят, уточнить свою точку зрения, а затем произвести окончательный выбор.

Пример 2.5. В рассматриваемой задаче найти оптимальную стратегию, пользуясь критерием Гурвица.

Решение. Возьмём (перевес в сторону пессимизма).

,

,

;

.

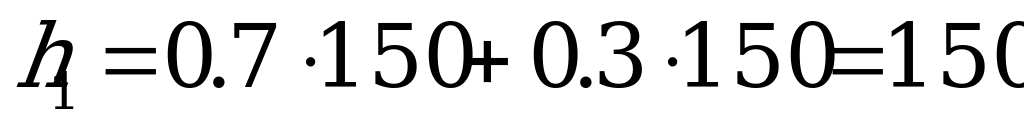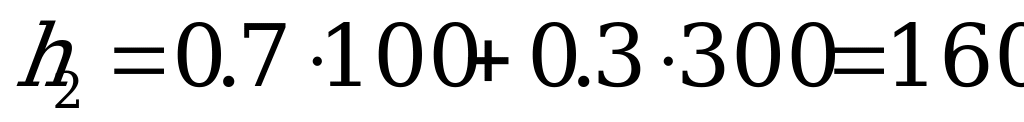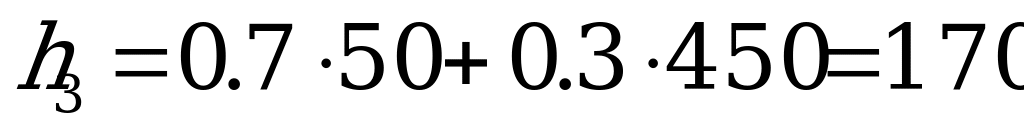
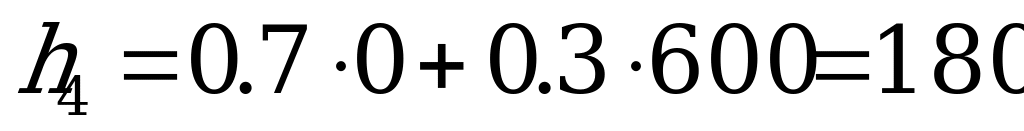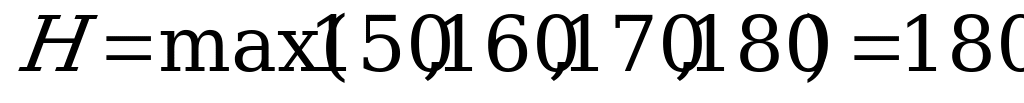Оптимальной стратегией по критерию Гурвица является .

В результате решение статистической игры по различным критериям чаще других рекомендовались стратегии и . Интуитивно ясно, что риск возрастает с увеличением мощности предприятия, поэтому предпочтём выбрать стратегию (построить предприятие мощностью 30 тыс. ед.продукции).