Тест №1
Метод координат
1 Вариант
Выберите верное утверждение.
А) Длина вектора 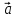 {x;y;z} вычисляется по формуле |
{x;y;z} вычисляется по формуле |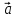 | =
| = 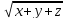 ;
;
Б) каждая координата вектора равна сумме соответствующих координат его начала и конца;
В) вектор называется координатным, если его длина равна единице;
Г) каждая координата середины отрезка равна полусумме соответствующих координат;
Д) любая точка пространства имеет положительные координаты.
2. На каком расстоянии от плоскости Оху находится точка А(2; -3; -5)?
а) 2; б) 3; в) ; г)10; д) 5.
; г)10; д) 5.
3. Даны точки А(5; 3; 2), В(3; -1; -4). Найдите длину вектора 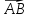 .
.
а) 2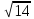 ; б)6
; б)6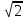 ; в)8; г)-12; д)2
; в)8; г)-12; д)2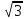 .
.
4. Даны точки А(-1; 2; 3) и В(1; -1; 4). Разложите вектор 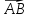 по координатным векторам.
по координатным векторам.
а) 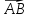 = -2
= -2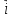 +3
+3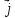 -
-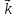 ; б)
; б)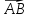 =0
=0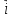 +
+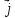 +7
+7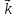 ; в)
; в)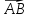 = 2
= 2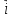 -3
-3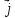 +
+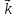 ; г)
; г)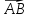 =3
=3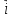 -2
-2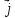 -
-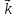 ; д)
; д)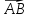 =
=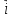 -3
-3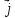 +2
+2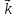 .
.
5. Выберите неверное утверждение.
а) Если у векторов координаты равны, то векторы равны;
б) если вектор 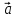 имеет координаты
имеет координаты 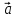 {m; n; p}, то его разложение по координатным векторам будет таким:
{m; n; p}, то его разложение по координатным векторам будет таким: 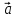 = n
= n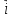 +p
+p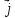 +m
+m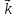 ;
;
в) каждая координата разности двух векторов равна разности соответствующих координат этих векторов;
г) любая точка пространства имеет три координаты;
д) расстояние между двумя точками М1(x1; y1; z1) и М2(x2; y2; z2) вычисляется по формуле d=.
6. Точки А(2; -1; 0) и В(-2; 3; 2) являются концами диаметра окружности. Найдите координаты центра окружности и ее радиус.
а) (0; 0; 2) и  ; б) (-2; 2; 1) и
; б) (-2; 2; 1) и 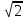 ; в) определить нельзя; г) (0; 1; 1) и 3; д) (-4; 4; 2) и
; в) определить нельзя; г) (0; 1; 1) и 3; д) (-4; 4; 2) и  .
.
7. Точки А(10; -10; -2), В(10; -6; -2) и С(8; -6; 0) являются вершинами треугольника. Вычислите его площадь.
а) 4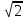 ; б) определить нельзя; в)64; г)4
; б) определить нельзя; в)64; г)4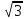 ; д)4
; д)4 .
.
8. Даны вектора 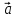 {4; x2-y2; 3},
{4; x2-y2; 3},  {4; 15; x+y}. Найдите x и y, если
{4; 15; x+y}. Найдите x и y, если 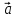 =
=  .
.
а) x= -4, y = 1; б) х = 4, у = -1; в) х = -4, у = -1; г) х = 4, у = 1;
д) определить нельзя.
9. Из предложенных векторов выберите некомпланарные векторы.
а)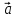 {-3; -3; 0),
{-3; -3; 0), 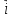 ,
, 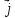 ; б)
; б)  {1; 0; -2},
{1; 0; -2}, 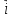 ,
, 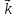 ; в)
; в)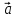 {1; -1; 2),
{1; -1; 2),  {-2; 0; 1},
{-2; 0; 1},  {5; -1; 0};
{5; -1; 0};
г)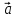 {-1; 1; -2),
{-1; 1; -2),  {2; 0; -1},
{2; 0; -1},  {-5; 1; 0}; д)
{-5; 1; 0}; д) {2; 0; -3},
{2; 0; -3}, 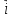 ,
, 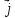 .
.
10. Точки А(4; 0; 1), В(4; 4; 1), С(0; 0; 5) и D(-1; 2; 0) являются вершинами пирамиды DABC. Найдите угол между боковым ребром и плоскостью основания.
а) arcsin0,2 ; б)arctg0,2
; б)arctg0,2 ; в) arccos0,2
; в) arccos0,2 ; г)arcctg0,2
; г)arcctg0,2 ;
;
д) определить нельзя.
2 Вариант
Выберите верное утверждение.
А) расстояние между двумя точками М1(x1; y1; z1) и М2(x2; y2; z2) вычисляется по формуле d=|x2-x1| + |y2-y1| + |z2-z1|;
Б) каждая координата середины отрезка равна модулю полуразности соответствующих координат его концов;
В) только координатные векторы являются единичными;
Г) каждая координата вектора равна разности соответствующих координат его конца и начала;
Д) любая точка пространства имеет неотрицательные координаты.
2. На каком расстоянии от плоскости Оzу находится точка B(-3; 2; -5)?
а) 2; б) 5; в) ; г)10; д) 3.
; г)10; д) 3.
3. Даны точки А(3; -1; -4), В(1; -4; 2). Найдите длину вектора  .
.
а) 7; б)3 ; в)1; г)-3; д)3
; в)1; г)-3; д)3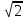 .
.
4. Даны точки А(2; -1; 3) и В(1; -2; 1). Разложите вектор  по координатным векторам.
по координатным векторам.
а)  = -
= -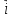 -
-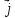 +2
+2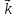 ; б)
; б) =
=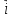 +
+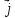 +2
+2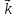 ; в)
; в) = -
= -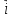 -
-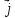 -2
-2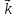 ; г)
; г) =
=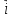 -2
-2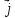 +
+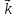 ; д)
; д) =2
=2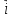 +
+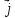 +
+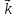 .
.
5. Выберите неверное утверждение.
а) Если векторы равны, то их координаты равны;
б) если вектор 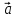 = n
= n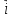 +p
+p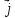 +m
+m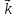 , то вектор
, то вектор 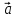 имеет координаты
имеет координаты 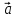 {m; n; p};
{m; n; p};
в) каждая координата середины отрезка равна полусумме соответствующих координат его концов;
г) любая точка пространства имеет три координаты;
д) длина вектора 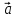 {x;y;z} вычисляется по формуле |
{x;y;z} вычисляется по формуле |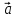 | =
| =  ;
;
6. Точки А(3; -4; 2), В(-3; 2; -4) и С(1; 3; -1) являются вершинами треугольника. Найдите длину медианы, проведенной из точки С.
а) 2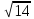 ; б) 2
; б) 2  ; в) определить нельзя; г);
; в) определить нельзя; г); д) 3.
д) 3.
7. Вычислите площадь треугольника, вершины которого имеют координаты
А(6; 14; -8), В(10; -6; 4), С(2; 6; -20).
а) 56 ; б) определить нельзя; в)62720; г)56
; б) определить нельзя; в)62720; г)56 ; д)56
; д)56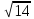 .
.
8. Даны вектора  { x2-y2; 4; 3},
{ x2-y2; 4; 3},  {3; 4; x-y}. Найдите x и y, если
{3; 4; x-y}. Найдите x и y, если  =
=  .
.
а) x= -2, y = 1; б) х = 2, у = 1; в) х = -2, у = -1; г) х = 2, у = -1;
д) определить нельзя.
9. Из предложенных векторов выберите коллинеарные векторы.
а)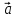 {1; -1; 3),
{1; -1; 3),  {2; 3; 15}; б)
{2; 3; 15}; б) 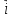 ,
, 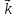 ; в)
; в) {0; 0; 0),
{0; 0; 0),  {-2; 9; 1};
{-2; 9; 1};
г) {2; 0; -1),
{2; 0; -1),  {-5; 1; 0}; д)
{-5; 1; 0}; д)
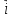 ,
, 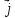 .
.
10. В основании пирамиды с вершиной в точке Е(-1; 2; -1) лежит ромб. Точки А(0; 0; 4), В(0; 4; 4), С(4; 4; 0), D(4; 0; 0) являются основаниями высот боковых граней. Найдите угол между плоскостью боковой грани и плоскостью основания.
а) arcsin0,2 ; б)arctg0,2
; б)arctg0,2 ; в) arccos0,2
; в) arccos0,2 ; г)arcctg0,2
; г)arcctg0,2 ;
;
д) определить нельзя.







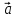 {x;y;z} вычисляется по формуле |
{x;y;z} вычисляется по формуле |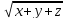 ;
; ; г)10; д) 5.
; г)10; д) 5.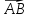 .
.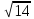 ; б)6
; б)6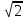 ; в)8; г)-12; д)2
; в)8; г)-12; д)2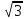 .
.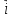 +3
+3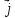 -
-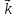 ; б)
; б)









