Тест №2
Скалярное произведение векторов
1 Вариант
Найдите угол между векторами 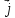 и
и 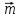 =2
=2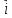 - 3
- 3 .
.
а) 0°; б) определить нельзя; в) 45°; г)90°; д)180°.
2. Вектор 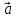 составляет с положительным направлением оси Ох угол 135°. Найдите абсциссу вектора
составляет с положительным направлением оси Ох угол 135°. Найдите абсциссу вектора 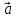 , если |
, если |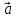 | =2.
| =2.
а) 2; б)-2; в)-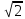 ; г)
; г)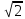 ; д) определить нельзя.
; д) определить нельзя.
3. Даны точки А(3; -2; 4), В(4; -1; 2), С(6; -3; 2), D(7; -3; 1). Найдите угол между векторами 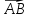 и
и 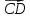 .
.
а) 150°; б)30°; в)45°; г)60°; д)120°.
4. Угол между векторами 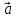 и
и 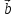 равен 60°. Найдите длину вектора 2
равен 60°. Найдите длину вектора 2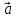 -
- 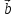 , если |
, если |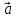 |=4,
|=4,
|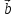 |= 2.
|= 2.
а)2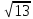 ; б)10; в)5
; б)10; в)5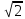 ; г)2
; г)2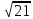 ; д)2
; д)2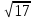 .
.
5. Выберите верное утверждение.
а) Угол между двумя векторами не может быть тупым;
б) скалярный квадрат вектора равен квадрату его длины;
в) скалярное произведение нулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны;
г) ненулевой вектор называется направляющим вектором прямой, если он лежит на прямой, перпендикулярной к данной прямой;
д) скалярное произведение векторов 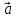 {x; y; z} и
{x; y; z} и 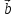 {m; n; p} выражается формулой
{m; n; p} выражается формулой 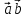 =xp+yn+zm.
=xp+yn+zm.
6. DABC – правильный тетраэдр. Упростите выражение
(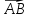 +
+ )*(
)*(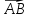 -
- )+
)+ *(
*( -
-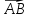 ).
).
а) 2; б)1; в)-1; г) определить нельзя; д) 0.
7.Дан куб ABCDA1B1C1D1 с ребром 2. Вычислите угол между векторами  и
и  , если М – центр грани BCC1B1.
, если М – центр грани BCC1B1.
а)arccos  ; б)180°-arccos
; б)180°-arccos ; в)arcsin
; в)arcsin ; г) -arcsin
; г) -arcsin ; д)90°.
; д)90°.
8. Дан куб ABCDA1B1C1D1 с ребром 2. Вычислите угол между прямыми АВ1 и ВС1.
а) 120°; б)90°; в)60°; г)150°; д)30°.
9. Ребро куба ABCDA1B1C1D1 равно 2, М – центр грани ВСС1В1. Вычислите угол между прямой MD и плоскостью ABC.
а) arccos  ; б) 180°-arccos
; б) 180°-arccos ; в)-arcsin
; в)-arcsin ; г) arcsin
; г) arcsin ; д)90°.
; д)90°.
10. Дан куб ABCDA1B1C1D1 с ребром 2. Вычислите расстояние между серединами отрезков АВ1 и ВС1.
а)2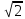 ; б)0,5
; б)0,5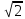 ; в)
; в) ; г)
; г)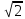 ; д)2.
; д)2.
2 Вариант
Найдите угол между векторами 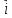 и
и  =-2
=-2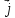 +
+  .
.
а) 180°; б) 45°; в) определить нельзя; г)90°; д)0°.
2. Вектор 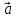 составляет с положительным направлением оси Оy угол 150°. Найдите ординату вектора
составляет с положительным направлением оси Оy угол 150°. Найдите ординату вектора 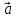 , если |
, если |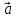 | =2
| =2 .
.
а) определить нельзя; б)- ; в)
; в) ; г)
; г) ; д) -3.
; д) -3.
3. Даны точки А(5; -8; -1), В(6; -8; -2), С(7; -5; -11), D(7; -7; -9). Найдите угол между векторами 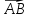 и
и 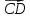 .
.
а) 120°; б)60°; в)45°; г)30°; д)150°.
4. Угол между единичными векторами 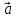 и
и 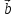 равен 60°. Найдите длину вектора 2
равен 60°. Найдите длину вектора 2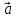 +
+ 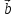 .
.
а) ; б)7; в)
; б)7; в) ; г)
; г) ; д)
; д) .
.
5. Выберите верное утверждение.
а) Если угол между двумя векторами равен 90°, то векторы называются перпендикулярными;
б) скалярным произведением двух векторов называется произведение их длин на синус угла между ними;
в) скалярный квадрат любого вектора есть число положительное;
г) от перемены мест сомножителей скалярное произведение изменяется;
д) скалярное произведение векторов 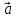 {x; y; z} и
{x; y; z} и 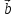 {m; n; p} выражается формулой
{m; n; p} выражается формулой 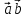 =xn+yp+zm.
=xn+yp+zm.
6. Все ребра пирамиды HPMKE равны. Упростите выражение
( +
+ )*(
)*( -
- ) +
) +  *(
*( +
+ ).
).
а) 2; б) определить нельзя; в)-1; г) 0; д) 1.
7.Дан куб ABCDA1B1C1D1 с ребром 4. Вычислите угол между векторами  и
и  , если М – центр грани ADA1D1.
, если М – центр грани ADA1D1.
а)arcsin  ; б)180°-arccos
; б)180°-arccos ; в)arccos
; в)arccos ; г) -arcsin
; г) -arcsin ; д)90°.
; д)90°.
8. Дан куб ABCDA1B1C1D1 с ребром 4. Вычислите угол между прямыми A1B и AD1.
а) 90°; б)120°; в)60°; г)150°; д)30°.
9. Ребро куба ABCDA1B1C1D1 равно 4, М – центр грани ADD1A1. Вычислите угол между прямой MB и плоскостью ABC.
а) arccos  ; б) 180°-arccos
; б) 180°-arccos ; в)arcsin
; в)arcsin ; г)- arcsin
; г)- arcsin ; д)90°.
; д)90°.
10. Дан куб ABCDA1B1C1D1 с ребром 4. Вычислите расстояние между серединами отрезков АВ1 и ВС1.
а)4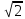 ; б)
; б)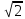 ; в)2
; в)2 ; г)2
; г)2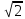 ; д)4.
; д)4.







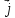 и
и 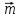 =2
=2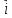 - 3
- 3 .
. 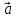 составляет с положительным направлением оси Ох угол 135°. Найдите абсциссу вектора
составляет с положительным направлением оси Ох угол 135°. Найдите абсциссу вектора 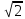 ; г)
; г)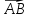 и
и 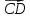 .
.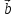 равен 60°. Найдите длину вектора 2
равен 60°. Найдите длину вектора 2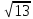 ; б)10; в)5
; б)10; в)5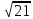 ; д)2
; д)2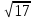 .
.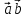 =xp+yn+zm.
=xp+yn+zm.









