Тетраэдр. Параллелепипед.

Тетраэдр. Параллелепипед.

Выполнил: преподаватель математики ГАПОУ «СЛТ» Горяшина А.А.

Определение тетраэдра

• Тетраэдр – это многогранник, состоящий из плоскости треугольника и точки не лежащий в этой плоскости, трех отрезков соединяющих эту точку с вершинами основания треугольника.

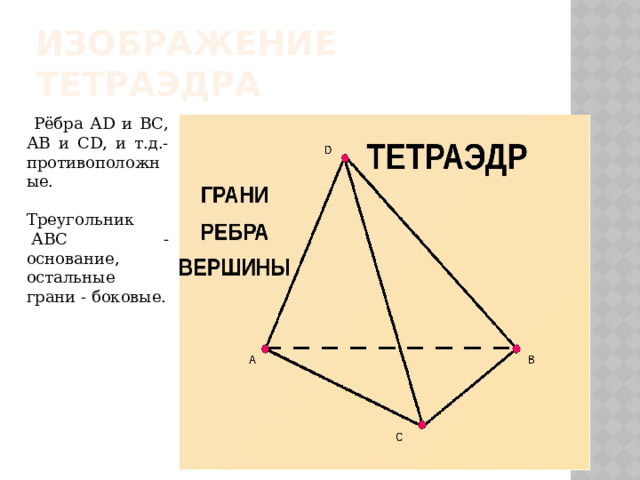
Изображение тетраэдра

Рёбра АD и ВС, АВ и CD, и т.д.- противоположные.

Треугольник  АВС - основание, остальные грани - боковые.

Составляющие тетраэдра

• Тетраэдр состоит:
• из вершин- их у него 4- А, B, C, D;
• из ребер- их у него 6- AB, BC, AC, AD, BD, CD;
• из граней- их у него 4- треугольники ∆АВС, ∆DАС, ∆DВС, ∆DАВ.

Тетраэдр в повседневной жизни

Параллелограмм

Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом

Свойства параллелограмма

Противоположные стороны параллелограмма равны: AB=DC,  BC=AD

Противоположные углы параллелограмма равны: ∟A=∟C, ∟B=∟D

Свойства параллелограмма

Диагонали параллелограмма точкой пересечения делятся пополам:BO=OD, AO=OC

Диагональ делит параллелограмм на два равных треугольника:

треугольники ABC и CDA равны.

Свойства параллелограмма

Сумма углов, прилежащих к одной стороне параллелограмма, равна 180⁰: ∟A+∟D=180°

  Накрест лежащие углы при диагонали равны:∟BAC=∟ACD, ∟BCA=∟CAD

Вывод параллелепипеда

Рассмотрим два равных параллелограмма ABCD и A 1 B 1 C 1 D 1 ,расположенных в параллельных плоскостях так, что отрезки AA 1,  BB 1,  CC 1  и DD 1  параллельны.

АВСDА 1 В 1 С 1 D 1  — параллелепипед.

Определение, свойства

• Параллелепипед- это шестигранник с параллельными и равными противоположными гранями.
• Противоположные грани параллелепипеда параллельны и равны.
• Все четыре диагонали пересекаются в одной точке и делятся в ней пополам.

Составляющие параллелепипеда:

• АВСDA 1 B 1 C 1 D 1 : поверхность, составленная из двух равных параллелограммов АВСD и A 1 B 1 C 1 D 1 , лежащих в параллельных плоскостях и четырёх параллелограммов.
• Все параллелограммы - грани, их стороны - рёбра, их вершины  - вершины параллелепипеда.
• Считается: АВСD и A 1 B 1 C 1 D 1  - основания, остальные грани - боковые.
•   Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда: A 1 C, D 1 B, AC 1 , DB 1 .

В основании у параллелепипеда:

Ромб Квадрат Прямоугольник

Все грани равные квадраты

Задача 1. Построить сечение плоскостью, проходящей через данные точки D, Е, K.

Построение:

S

1. DE

2. ЕК

3. ЕК ∩ АС = F

4. FD

5. FD ∩ BС = M

6. KM

E

DЕKМ – искомое сечение

K

F

А

С

M

D

В

Спасибо за внимание!