Тексты на английском + перевод на тему "История развития математики"

ALGEBRA

Introduction

Algebra, branch of mathematics in which letters are used to represent basic arithmetic relations. As in arithmetic, the basic operations of algebra are addition, subtraction, multiplication, division, and the extraction of roots. Arithmetic, however, cannot generalize mathematical relations such as the Pythagorean theorem, which states that the sum of the squares of the sides of any right triangle is also a square. Arithmetic can only produce specific instances of these relations (for example, 3, 4, and 5, where 3² + 4² = 5²). But algebra can make a purely general statement that fulfills the conditions of the theorem: a² + b² = c². Any number multiplied by itself is termed squared and is indicated by a superscript number 2. For example, 3 × 3 is notated 3²; similarly, a × a is equivalent to a² (see Exponent; Power; Root).

Classical algebra, which is concerned with solving equations, uses symbols instead of specific numbers and uses arithmetic operations to establish ways of handling symbols (see Equation; Equations, Theory of). Modern algebra has evolved from classical algebra by increasing its attention to the structures within mathematics. Mathematicians consider modern algebra to be a set of objects with rules for connecting or relating them. As such, in its most general form, algebra may fairly be described as the language of mathematics.

History

The history of algebra began in ancient Egypt and Babylon, where people learned to solve linear (ax = b) and quadratic (ax² + bx = c) equations, as well as indeterminate equations such as x² + y² = z², whereby several unknowns are involved. The ancient Babylonians solved arbitrary quadratic equations by essentially the same procedures taught today. They also could solve some indeterminate equations.

The Alexandrian mathematicians Hero of Alexandria and Diophantus continued the traditions of Egypt and Babylon, but Diophantus's book Arithmetica is on a much higher level and gives many surprising solutions to difficult indeterminate equations. This ancient knowledge of solutions of equations in turn found a home early in the Islamic world, where it was known as the “science of restoration and balancing.” (The Arabic word for restoration, al-jabru, is the root of the word algebra.) In the 9th century, the Arab mathematician al-Khwārizmī wrote one of the first Arabic algebras, a systematic exposé of the basic theory of equations, with both examples and proofs. By the end of the 9th century, the Egyptian mathematician Abu Kamil had stated and proved the basic laws and identities of algebra and solved such complicated problems as finding x, y, and z such that x + y + z = 10, x² + y² = z², and xz = y².

Ancient civilizations wrote out algebraic expressions using only occasional abbreviations, but by medieval times Islamic mathematicians were able to talk about arbitrarily high powers of the unknown x, and work out the basic algebra of polynomials (without yet using modern symbolism). This included the ability to multiply, divide, and find square roots of polynomials as well as a knowledge of the binomial theorem. The Persian mathematician, astronomer, and poet Omar Khayyam showed how to express roots of cubic equations by line segments obtained by intersecting conic sections, but he could not find a formula for the roots. A Latin translation of Al-Khwarizmi's Algebra appeared in the 12th century. In the early 13th century, the great Italian mathematician Leonardo Fibonacci achieved a close approximation to the solution of the cubic equation x³ + 2x² + cx = d. Because Fibonacci had traveled in Islamic lands, he probably used an Arabic method of successive approximations.

Early in the 16th century, the Italian mathematicians Scipione del Ferro, Niccolò Tartaglia, and Gerolamo Cardano solved the general cubic equation in terms of the constants appearing in the equation. Cardano's pupil, Ludovico Ferrari, soon found an exact solution to equations of the fourth degree, and as a result, mathematicians for the next several centuries tried to find a formula for the roots of equations of degree five, or higher. Early in the 19th century, however, the Norwegian mathematician Niels Abel and the French mathematician Évariste Galois proved that no such formula exists.

An important development in algebra in the 16th century was the introduction of symbols for the unknown and for algebraic powers and operations. As a result of this development, Book III of La géometrie (1637), written by the French philosopher and mathematician René Descartes, looks much like a modern algebra text. Descartes's most significant contribution to mathematics, however, was his discovery of analytic geometry, which reduces the solution of geometric problems to the solution of algebraic ones. His geometry text also contained the essentials of a course on the theory of equations, including his so-called rule of signs for counting the number of what Descartes called the “true” (positive) and “false” (negative) roots of an equation. Work continued through the 18th century on the theory of equations, but not until 1799 was the proof published, by the German mathematician Carl Friedrich Gauss, showing that every polynomial equation has at least one root in the complex plane (see Number: Complex Numbers).

By the time of Gauss, algebra had entered its modern phase. Attention shifted from solving polynomial equations to studying the structure of abstract mathematical systems whose axioms were based on the behavior of mathematical objects, such as complex numbers, that mathematicians encountered when studying polynomial equations. Two examples of such systems are groups (see Group) and quaternions, which share some of the properties of number systems but also depart from them in important ways. Groups began as systems of permutations and combinations of roots of polynomials, but they became one of the chief unifying concepts of 19th-century mathematics. Important contributions to their study were made by the French mathematicians Galois and Augustin Cauchy, the British mathematician Arthur Cayley, and the Norwegian mathematicians Niels Abel and Sophus Lie. Quaternions were discovered by British mathematician and astronomer William Rowan Hamilton, who extended the arithmetic of complex numbers to quaternions while complex numbers are of the form a + bi, quaternions are of the form a + bi + cj + dk.

Immediately after Hamilton's discovery, the German mathematician Hermann Grassmann began investigating vectors. Despite its abstract character, American physicist J. W. Gibbs recognized in vector algebra a system of great utility for physicists, just as Hamilton had recognized the usefulness of quaternions. The widespread influence of this abstract approach led George Boole to write The Laws of Thought (1854), an algebraic treatment of basic logic. Since that time, modern algebra—also called abstract algebra—has continued to develop. Important new results have been discovered, and the subject has found applications in all branches of mathematics and in many of the sciences as well.

Operation with polynomials

In operating with polynomials, the assumption is that the usual laws of the arithmetic of numbers hold. In arithmetic, the numbers used are the set of rational numbers (see Number; Number Theory). Arithmetic alone cannot go beyond this, but algebra and geometry can include both irrational numbers, such as the square root of 2, and complex numbers. The set of all rational and irrational numbers taken together constitutes the set of what are called real numbers.

Laws of addition

The sum of any two real numbers A1. a and b is again a real number, denoted a + b. The real numbers are closed under the operations of addition, subtraction, multiplication, division, and the extraction of roots; this means that applying any of these operations to real numbers yields a quantity that also is a real number.

No matter how terms are grouped in carrying out additions, the sum A2. will always be the same: (a + b) + c = a + (b + c). This is called the associative law of addition.

Given any real number A3. a, there is a real number zero (0) called the additive identity, such that a + 0 = 0 + a = a.

Given any real number A4. a, there is a number (-a), called the additive inverse of a, such that (a) + (-a) = 0.

No matter in what order addition is carried out, the sum will A5. always be the same: a + b = b + a. This is called the commutative law of addition.

Any set of numbers obeying laws A1 through A4 is said to form a group. If the set also obeys A5, it is said to be an Abelian, or commutative, group.

Laws of multiplication

Laws similar to those for addition also apply to multiplication. Special attention should be given to the multiplicative identity and inverse, M3 and M4.

The product of any two real numbers M1. a and b is again a real number, denoted a·b or ab.

No matter how terms are grouped in carrying out multiplications, M2. the product will always be the same: (ab)c = a(bc). This is called the associative law of multiplication.

Given any real number M3. a, there is a number one (1) called the multiplicative identity, such that a(1) = 1(a) = a.

Given any nonzero real number M4. a, there is a number (a^-1), or (1/a), called the multiplicative inverse, such that a(a^-1) = (a^-1)a = 1.

No matter in what order multiplication is carried out, the product M5. will always be the same: ab = ba. This is called the commutative law of multiplication.

Any set of elements obeying these five laws is said to be an Abelian, or commutative, group under multiplication. The set of all real numbers, excluding zero (because division by zero is inadmissible), forms such a commutative group under multiplication.

Distributive laws

Another important property of the set of real numbers links addition and multiplication in two distributive laws as follows:

 D1. a(b + c) = ab + ac

 D2. (b + c)a = ba + ca

Any set of elements with an equality relation and for which two operations (such as addition and multiplication) are defined, and which obeys all the laws for addition A1 through A5, the laws for multiplication M1 through M5, and the distributive laws D1 and D2, constitutes a field.

NUMERALS

Introduction

Numerals, signs or symbols for graphic representation of numbers. The earliest forms of number notation were simply groups of straight lines, either vertical or horizontal, each line corresponding to the number 1. Such a system is inconvenient when dealing with large numbers, and as early as 3400 bc in Egypt and 3000 bc in Mesopotamia a special symbol was adopted for the number 10. The addition of this second number symbol made it possible to express the number 11 with 2 instead of 11 individual symbols and the number 99 with 18 instead of 99 individual symbols. Later numeral systems introduced extra symbols for a number between 1 and 10, usually either 4 or 5, and additional symbols for numbers greater than 10. In Babylonian cuneiform notation the numeral used for 1 was also used for 60 and for powers of 60; the value of the numeral was indicated by its context. This was a logical arrangement from the mathematical point of view because 60 ⁰ = 1, 60¹ = 60, and 60² = 3600. The Egyptian hieroglyphic system used special symbols for 10, 100, 1000, and 10,000.

The ancient Greeks had two parallel systems of numerals. The earlier of these was based on the initial letters of the names of numbers: The number 5 was indicated by the letter pi; 10 by the letter delta; 100 by the antique form of the letter H; 1000 by the letter chi; and 10,000 by the letter mu. The later system, which was first introduced about the 3rd century bc, employed all the letters of the Greek alphabet plus three letters borrowed from the Phoenician alphabet as number symbols. The first nine letters of the alphabet were used for the numbers 1 to 9, the second nine letters for the tens from 10 to 90, and the last nine letters for the hundreds from 100 to 900. Thousands were indicated by placing a bar to the left of the appropriate numeral, and tens of thousands by placing the appropriate letter over the letter M. The late Greek system had the advantage that large numbers could be expressed with a minimum of symbols, but it had the disadvantage of requiring the user to memorize a total of 27 symbols.

Roman numerals

The system of number symbols created by the Romans had the merit of expressing all numbers from 1 to 1,000,000 with a total of seven symbols: I for 1, V for 5, X for 10, L for 50, C for 100, D for 500, and M for 1000. Roman numerals are read from left to right. The symbols representing the largest quantities are placed at the left; immediately to the right of those are the symbols representing the next largest quantities, and so on. The symbols are usually added together. For example, LX = 60, and MMCIII = 2103. When a numeral is smaller than the numeral to the right, however, the numeral on the left should be subtracted from the numeral on the right. For instance, XIV = 14 and IX = 9. represents 1,000,000—a small bar placed over the numeral multiplies the numeral by 1000. Thus, theoretically, it is possible, by using an infinite number of bars, to express the numbers from 1 to infinity. In practice, however, one bar is usually used; two are rarely used, and more than two are almost never used. Roman numerals are still used today, more than 2000 years after their introduction. The Roman system's one drawback, however, is that it is not suitable for rapid written calculations.

Arabic numerals

The common system of number notation in use in most parts of the world today is the Arabic system. This system was first developed by the Hindus and was in use in India in the 3rd century bc. At that time the numerals 1, 4, and 6 were written in substantially the same form used today. The Hindu numeral system was probably introduced into the Arab world about the 7th or 8th century ad . The first recorded use of the system in Europe was in ad976.

The important innovation in the Arabic system was the use of positional notation, in which individual number symbols assume different values according to their position in the written numeral. Positional notation is made possible by the use of a symbol for zero. The symbol 0 makes it possible to differentiate between 11, 101, and 1001 without the use of additional symbols, and all numbers can be expressed in terms of ten symbols, the numerals from 1 to 9 plus 0. Positional notation also greatly simplifies all forms of written numerical calculation.

AXIOM

Axiom, in logic and mathematics, a basic principle that is assumed to be true without proof. The use of axioms in mathematics stems from the ancient Greeks, most probably during the 5th century bc, and represents the beginnings of pure mathematics as it is known today. Examples of axioms are the following: “No sentence can be true and false at the same time” (the principle of contradiction); “If equals are added to equals, the sums are equal”; “The whole is greater than any of its parts.” Logic and pure mathematics begin with such unproved assumptions from which other propositions (theorems) are derived. This procedure is necessary to avoid circularity, or an infinite regression in reasoning. The axioms of any system must be consistent with one another, that is, they should not lead to contradictions. They should be independent in the sense that they cannot be derived from one another. They should also be few in number. Axioms have sometimes been interpreted as self-evident truths. The present tendency is to avoid this claim and simply to assert that an axiom is assumed to be true without proof in the system of which it is a part.

The terms axiom and postulate are often used synonymously. Sometimes the word axiom is used to refer to basic principles that are assumed by every deductive system, and the term postulate is used to refer to first principles peculiar to a particular system, such as Euclidean geometry. Infrequently, the word axiom is used to refer to first principles in logic, and the term postulate is used to refer to first principles in mathematics.

VECTOR (MATHEMATICS)

Vector (mathematics), quantity having both magnitude and direction. For example, an ordinary quantity, or scalar, can be exemplified by the distance 6 km; a vector quantity can be exemplified by the term 6 km north. Vectors are usually represented by directed line segments, such as in the diagram below; the length of the line segment is a measure of the vector quantity, and its direction is the same as that of the vector.

The simplest use of vectors and calculation by means of vectors is illustrated in the diagram, drawn to represent a boat moving across a stream. Vector a, or , indicates the motion of the boat in the course of a given interval of time if it were moving through still water; vector b, or , shows the drift or flow of the current during the same period of time. The actual path of travel of the boat under the influence of its own propulsion and of the current is represented by vector c, or . By the use of vectors any type of problem involving the motion of an object being acted on by several forces can be solved graphically.

This method of problem solution, known as vector addition, is performed as follows. A vector representing one force is drawn from the origin O in the proper direction. The length of the vector is made to agree with any convenient arbitrary scale, such as a given number of centimeters to the kilometer. In the diagram the rate of rowing was 2.2 km/h, the time rowed was 1 hr, and the scale is 1 cm to 1 km. Therefore, the line is drawn as 2.2 cm to equal 2.2 km. The current speed of 6 km/h is then represented by a vector that is 6 cm long, indicating a distance of 6 km that the current moved during 1 hr. This second vector is drawn with its origin at the end of vector a in a direction parallel to the flow of the current. The point B at the end of the second vector represents the actual position of the boat at the end of 1 hr of travel, and the actual distance traveled is represented by the length (in this case, about 6.4 km) of the vector c, or .

Problems in vector addition and subtraction such as the one above can be easily solved by graphic methods and can also be calculated by means of trigonometry. This type of calculation is useful in solving problems in navigation and motion as well as in mechanics and other branches of physics. In present-day advanced mathematics, a vector is considered an ordered set of quantities with appropriate rules of manipulation. Vector analysis, that is, the algebra, geometry, and calculus of vector quantities, enters into the applied mathematics of every field of science and engineering.

SEQUENCE AND SERIES

Sequence and Series, in mathematics, an ordered succession of numbers or other quantities, and the indicated sum of such a succession, respectively.

A sequence is represented as a₁, a₂..., a_n, .... The as are numbers or quantities, distinct or not; a₁ is the first term, a ₂ the second term, and so on. If the expression has a last term, the sequence is finite; otherwise, it is infinite. A sequence is established or defined only if a rule is given that determines the nth term for every positive integer n; this rule may be given as a formula for the nth term. For example, all the positive integers, in natural order, form an infinite sequence; this sequence is defined by the formula a_n=n. The formula a_n = n² determines the sequence 1, 4, 9, 16, .... The rule of starting with 0, 1, then letting each term be the sum of the two preceding terms determines the sequence 0, 1, 1, 2, 3, 5, 8, 13, ...; this is known as the Fibonacci sequence.

Important types of sequences include arithmetic sequences (also known as arithmetic progressions) in which the differences between successive terms are constant, and geometric sequences (also known as geometric progressions) in which the ratios of successive terms are constant. Examples arise when a sum of money is invested. If the money is invested at a simple interest of 8 percent, then after n years an initial principal of P dollars grows to a_n = P + n × (0.08)P dollars. Since (0.08) P dollars is added each year, the amounts a_n form an arithmetic progression. If the interest is instead compounded, the amounts present after a sequence of years form a geometric progression, g_n = P × (1.08)ⁿ. In both of these cases, it is clear that a_n and g_n will eventually become larger than any preassigned whole number N, however large N may be.

Terms in a sequence, however, do not always increase without limit. For example, as n increases, the sequence a_n = 1/n approaches 0 as a limiting value, and b_n = A + B/n approaches A. In any such case some finite number L exists such that whatever tolerance e is specified, the values of the sequence all eventually lie within a distance e of L. For example, in the case of the sequence 2 + (-1)ⁿ/2n,L = 2. Even if e is as small as 1/10,000, it can be seen that if n is greater than 5000, all values of n are within e of 2. The number L is called the limit of the sequence, since even though individual terms of the sequence may be bigger or smaller than L, the terms eventually cluster closer and closer to L. When the sequence has a limit L, it is said to converge to L. For the sequence a_n, for example, this is written as lim a_n = L, which is read as “the limit of a_n as n goes to infinity is L.”

The term series refers to the indicated sum, a₁ + a₂ + ... + a_n, or a₁ + a₂ + ... + a_n + ..., of the terms of a sequence. A series is either finite or infinite, depending on whether the corresponding sequence of terms is finite or infinite.

The sequence s₁ = a_1,s₂ = a₁ + a₂, s₃ = a₁ + a₂ + a₃, ..., s_n = a₁ + a₂ + ... + a_n, ..., is called the sequence of partial sums of the series a₁ + a₂ + ... + a_n + .... The series converges or diverges as the sequence of partial sums converges or diverges. A constant-term series is one in which the terms are numbers; a series of functions is one in which the terms are functions of one or more variables. In particular, a power series is the series a₀ + a₁(x - c) + a₂(x - c)² + ... + a_n(x - c)ⁿ + ..., in which c and the as are constants. In the case of power series, the problem is to describe what values of x they converge for. If a series converges for some x, then the set of all x for which it converges consists of a point or some connected interval. The basic theory of convergence was worked out by the French mathematician Augustin Louis Cauchy in the 1820s.

The theory and application of infinite series are important in virtually every branch of pure and applied mathematics.

ARCHITECTURE (COMPUTER SCIENCE)

Introduction

Architecture (computer science), a general term referring to the structure of all or part of a computer system. The term also covers the design of system software, such as the operating system (the program that controls the computer), as well as referring to the combination of hardware and basic software that links the machines on a computer network. Computer architecture refers to an entire structure and to the details needed to make it functional. Thus, computer architecture covers computer systems, microprocessors, circuits, and system programs. Typically the term does not refer to application programs, such as spreadsheets or word processing, which are required to perform a task but not to make the system run.

Design elements

In designing a computer system, architects consider five major elements that make up the system's hardware: the arithmetic/logic unit, control unit, memory, input, and output. The arithmetic/logic unit performs arithmetic and compares numerical values. The control unit directs the operation of the computer by taking the user instructions and transforming them into electrical signals that the computer's circuitry can understand. The combination of the arithmetic/logic unit and the control unit is called the central processing unit (CPU). The memory stores instructions and data. The input and output sections allow the computer to receive and send data, respectively.

Different hardware architectures are required because of the specialized needs of systems and users. One user may need a system to display graphics extremely fast, while another system may have to be optimized for searching a database or conserving battery power in a laptop computer.

In addition to the hardware design, the architects must consider what software programs will operate the system. Software, such as programming languages and operating systems, makes the details of the hardware architecture invisible to the user. For example, computers that use the C programming language or a UNIX operating system may appear the same from the user's viewpoint, although they use different hardware architectures.

Processing architecture

When a computer carries out an instruction, it proceeds through five steps. First, the control unit retrieves the instruction from memory—for example, an instruction to add two numbers. Second, the control unit decodes the instructions into electronic signals that control the computer. Third, the control unit fetches the data (the two numbers). Fourth, the arithmetic/logic unit performs the specific operation (the addition of the two numbers). Fifth, the control unit saves the result (the sum of the two numbers).

Early computers used only simple instructions because the cost of electronics capable of carrying out complex instructions was high. As this cost decreased in the 1960s, more complicated instructions became possible. Complex instructions (single instructions that specify multiple operations) can save time because they make it unnecessary for the computer to retrieve additional instructions. For example, if seven operations are combined in one instruction, then six of the steps that fetch instructions are eliminated and the computer spends less time processing that operation. Computers that combine several instructions into a single operation are called complex instruction set computers (CISC).

However, most programs do not often use complex instructions, but consist mostly of simple instructions. When these simple instructions are run on CISC architectures they slow down processing because each instruction—whether simple or complex—takes longer to decode in a CISC design. An alternative strategy is to return to designs that use only simple, single-operation instruction sets and make the most frequently used operations faster in order to increase overall performance. Computers that follow this design are called reduced instruction set computers (RISC).

RISC designs are especially fast at the numerical computations required in science, graphics, and engineering applications. CISC designs are commonly used for nonnumerical computations because they provide special instruction sets for handling character data, such as text in a word processing program. Specialized CISC architectures, called digital signal processors, exist to accelerate processing of digitized audio and video signals.

Open and closed architectures

The CPU of a computer is connected to memory and to the outside world by means of either an open or a closed architecture. An open architecture can be expanded after the system has been built, usually by adding extra circuitry, such as a new microprocessor computer chip connected to the main system. The specifications of the circuitry are made public, allowing other companies to manufacture these expansion products.

Closed architectures are usually employed in specialized computers that will not require expansion—for example, computers that control microwave ovens. Some computer manufacturers have used closed architectures so that their customers can purchase expansion circuitry only from them. This allows the manufacturer to charge more and reduces the options for the consumer.

Network architecture

Computers communicate with other computers via networks. The simplest network is a direct connection between two computers. However, computers can also be connected over large networks, allowing users to exchange data, communicate via electronic mail, and share resources such as printers.

Computers can be connected in several ways. In a ring configuration, data are transmitted along the ring and each computer in the ring examines this data to determine if it is the intended recipient. If the data are not intended for a particular computer, the computer passes the data to the next computer in the ring. This process is repeated until the data arrive at their intended destination. A ring network allows multiple messages to be carried simultaneously, but since each message is checked by each computer, data transmission is slowed.

In a bus configuration, computers are connected through a single set of wires, called a bus. One computer sends data to another by broadcasting the address of the receiver and the data over the bus. All the computers in the network look at the address simultaneously, and the intended recipient accepts the data. A bus network, unlike a ring network, allows data to be sent directly from one computer to another. However, only one computer at a time can transmit data. The others must wait to send their messages.

In a star configuration, computers are linked to a central computer called a hub. A computer sends the address of the receiver and the data to the hub, which then links the sending and receiving computers directly. A star network allows multiple messages to be sent simultaneously, but it is more costly because it uses an additional computer, the hub, to direct the data.

Recent advances

One problem in computer architecture is caused by the difference between the speed of the CPU and the speed at which memory supplies instructions and data. Modern CPUs can process instructions in 3 nanoseconds (3 billionths of a second). A typical memory access, however, takes 100 nanoseconds and each instruction may require multiple accesses. To compensate for this disparity, new computer chips have been designed that contain small memories, called caches, located near the CPU. Because of their proximity to the CPU and their small size, caches can supply instructions and data faster than normal memory. Cache memory stores the most frequently used instructions and data and can greatly increase efficiency.

Although a larger cache memory can hold more data, it also becomes slower. To compensate, computer architects employ designs with multiple caches. The design places the smallest and fastest cache nearest the CPU and locates a second larger and slower cache farther away. This arrangement allows the CPU to operate on the most frequently accessed instructions and data at top speed and to slow down only slightly when accessing the secondary cache. Using separate caches for instructions and data also allows the CPU to retrieve an instruction and data simultaneously.

Another strategy to increase speed and efficiency is the use of multiple arithmetic/logic units for simultaneous operations, called superscalar execution. In this design, instructions are acquired in groups. The control unit examines each group to see if it contains instructions that can be performed together. Some designs execute as many as six operations simultaneously. It is rare, however, to have this many instructions run together, so on average the CPU does not achieve a six-fold increase in performance.

Multiple computers are sometimes combined into single systems called parallel processors. When a machine has more than one thousand arithmetic/logic units, it is said to be massively parallel. Such machines are used primarily for numerically intensive scientific and engineering computation. Parallel machines containing as many as sixteen thousand computers have been constructed.

COMPUTER SCIENCE

Introduction

Computer Science, study of the theory, experimentation, and engineering that form the basis for the design and use of computers—devices that automatically process information. Computer science traces its roots to work done by English mathematician Charles Babbage, who first proposed a programmable mechanical calculator in 1837. Until the advent of electronic digital computers in the 1940s, computer science was not generally distinguished as being separate from mathematics and engineering. Since then it has sprouted numerous branches of research that are unique to the discipline.

The development of computer science

Early work in the field of computer science during the late 1940s and early 1950s focused on automating the process of making calculations for use in science and engineering. Scientists and engineers developed theoretical models of computation that enabled them to analyze how efficient different approaches were in performing various calculations. Computer science overlapped considerably during this time with the branch of mathematics known as numerical analysis, which examines the accuracy and precision of calculations.

As the use of computers expanded between the 1950s and the 1970s, the focus of computer science broadened to include simplifying the use of computers through programming languages—artificial languages used to program computers, and operating systems—computer programs that provide a useful interface between a computer and a user. During this time, computer scientists were also experimenting with new applications and computer designs, creating the first computer networks, and exploring relationships between computation and thought.

In the 1970s, computer chip manufacturers began to mass produce microprocessors—the electronic circuitry that serves as the main information processing center in a computer. This new technology revolutionized the computer industry by dramatically reducing the cost of building computers and greatly increasing their processing speed. The microprocessor made possible the advent of the personal computer, which resulted in an explosion in the use of computer applications. Between the early 1970s and 1980s, computer science rapidly expanded in an effort to develop new applications for personal computers and to drive the technological advances in the computing industry. Much of the earlier research that had been done began to reach the public through personal computers, which derived most of their early software from existing concepts and systems.

Computer scientists continue to expand the frontiers of computer and information systems by pioneering the designs of more complex, reliable, and powerful computers; enabling networks of computers to efficiently exchange vast amounts of information; and seeking ways to make computers behave intelligently. As computers become an increasingly integral part of modern society, computer scientists strive to solve new problems and invent better methods of solving current problems.

The goals of computer science range from finding ways to better educate people in the use of existing computers to highly speculative research into technologies and approaches that may not be viable for decades. Underlying all of these specific goals is the desire to better the human condition today and in the future through the improved use of information.

Theory and experiment

Computer science is a combination of theory, engineering, and experimentation. In some cases, a computer scientist develops a theory, then engineers a combination of computer hardware and software based on that theory, and experimentally tests it. An example of such a theory-driven approach is the development of new software engineering tools that are then evaluated in actual use. In other cases, experimentation may result in new theory, such as the discovery that an artificial neural network exhibits behavior similar to neurons in the brain, leading to a new theory in neurophysiology.

It might seem that the predictable nature of computers makes experimentation unnecessary because the outcome of experiments should be known in advance. But when computer systems and their interactions with the natural world become sufficiently complex, unforeseen behaviors can result. Experimentation and the traditional scientific method are thus key parts of computer science.

Major branches of computer science

Computer science can be divided into four main fields: software development, computer architecture (hardware), human- computer interfacing (the design of the most efficient ways for humans to use computers), and artificial intelligence (the attempt to make computers behave intelligently). Software development is concerned with creating computer programs that perform efficiently. Computer architecture is concerned with developing optimal hardware for specific computational needs. The areas of artificial intelligence (AI) and human-computer interfacing often involve the development of both software and hardware to solve specific problems.

Software development

In developing computer software, computer scientists and engineers study various areas and techniques of software design, such as the best types of programming languages and algorithms (see below) to use in specific programs, how to efficiently store and retrieve information, and the computational limits of certain software-computer combinations. Software designers must consider many factors when developing a program. Often, program performance in one area must be sacrificed for the sake of the general performance of the software. For instance, since computers have only a limited amount of memory, software designers must limit the number of features they include in a program so that it will not require more memory than the system it is designed for can supply.

Software engineering is an area of software development in which computer scientists and engineers study methods and tools that facilitate the efficient development of correct, reliable, and robust computer programs. Research in this branch of computer science considers all the phases of the software life cycle, which begins with a formal problem specification, and progresses to the design of a solution, its implementation as a program, testing of the program, and program maintenance. Software engineers develop software tools and collections of tools called programming environments to improve the development process. For example, tools can help to manage the many components of a large program that is being written by a team of programmers.

Algorithms and data structures are the building blocks of computer programs. An algorithm is a precise step-by-step procedure for solving a problem within a finite time and using a finite amount of memory. Common algorithms include searching a collection of data, sorting data, and numerical operations such as matrix multiplication. Data structures are patterns for organizing information, and often represent relationships between data values. Some common data structures are called lists, arrays, records, stacks, queues, and trees.

Computer scientists continue to develop new algorithms and data structures to solve new problems and improve the efficiency of existing programs. One area of theoretical research is called algorithmic complexity. Computer scientists in this field seek to develop techniques for determining the inherent efficiency of algorithms with respect to one another. Another area of theoretical research called computability theory seeks to identify the inherent limits of computation.

Software engineers use programming languages to communicate algorithms to a computer. Natural languages such as English are ambiguous—meaning that their grammatical structure and vocabulary can be interpreted in multiple ways—so they are not suited for programming. Instead, simple and unambiguous artificial languages are used. Computer scientists study ways of making programming languages more expressive, thereby simplifying programming and reducing errors. A program written in a programming language must be translated into machine language (the actual instructions that the computer follows). Computer scientists also develop better translation algorithms that produce more efficient machine language programs.

Databases and information retrieval are related fields of research. A database is an organized collection of information stored in a computer, such as a company’s customer account data. Computer scientists attempt to make it easier for users to access databases, prevent access by unauthorized users, and improve access speed. They are also interested in developing techniques to compress the data, so that more can be stored in the same amount of memory. Databases are sometimes distributed over multiple computers that update the data simultaneously, which can lead to inconsistency in the stored information. To address this problem, computer scientists also study ways of preventing inconsistency without reducing access speed.

Information retrieval is concerned with locating data in collections that are not clearly organized, such as a file of newspaper articles. Computer scientists develop algorithms for creating indexes of the data. Once the information is indexed, techniques developed for databases can be used to organize it. Data mining is a closely related field in which a large body of information is analyzed to identify patterns. For example, mining the sales records from a grocery store could identify shopping patterns to help guide the store in stocking its shelves more effectively.

Operating systems are programs that control the overall functioning of a computer. They provide the user interface, place programs into the computer’s memory and cause it to execute them, control the computer’s input and output devices, manage the computer’s resources such as its disk space, protect the computer from unauthorized use, and keep stored data secure. Computer scientists are interested in making operating systems easier to use, more secure, and more efficient by developing new user interface designs, designing new mechanisms that allow data to be shared while preventing access to sensitive data, and developing algorithms that make more effective use of the computer’s time and memory.

The study of numerical computation involves the development of algorithms for calculations, often on large sets of data or with high precision. Because many of these computations may take days or months to execute, computer scientists are interested in making the calculations as efficient as possible. They also explore ways to increase the numerical precision of computations, which can have such effects as improving the accuracy of a weather forecast. The goals of improving efficiency and precision often conflict, with greater efficiency being obtained at the cost of precision and vice versa.

Symbolic computation involves programs that manipulate nonnumeric symbols, such as characters, words, drawings, algebraic expressions, encrypted data (data coded to prevent unauthorized access), and the parts of data structures that represent relationships between values. One unifying property of symbolic programs is that they often lack the regular patterns of processing found in many numerical computations. Such irregularities present computer scientists with special challenges in creating theoretical models of a program’s efficiency, in translating it into an efficient machine language program, and in specifying and testing its correct behavior.

Computer architecture

Computer architecture is the design and analysis of new computer systems. Computer architects study ways of improving computers by increasing their speed, storage capacity, and reliability, and by reducing their cost and power consumption. Computer architects develop both software and hardware models to analyze the performance of existing and proposed computer designs, then use this analysis to guide development of new computers. They are often involved with the engineering of a new computer because the accuracy of their models depends on the design of the computer’s circuitry. Many computer architects are interested in developing computers that are specialized for particular applications such as image processing, signal processing, or the control of mechanical systems. The optimization of computer architecture to specific tasks often yields higher performance, lower cost, or both.

Artificial intelligence

Artificial intelligence (AI) research seeks to enable computers and machines to mimic human intelligence and sensory processing ability, and models human behavior with computers to improve our understanding of intelligence. The many branches of AI research include machine learning, inference, cognition, knowledge representation, problem solving, case-based reasoning, natural language understanding, speech recognition, computer vision, and artificial neural networks.

A key technique developed in the study of artificial intelligence is to specify a problem as a set of states, some of which are solutions, and then search for solution states. For example, in chess, each move creates a new state. If a computer searched the states resulting from all possible sequences of moves, it could identify those that win the game. However, the number of states associated with many problems (such as the possible number of moves needed to win a chess game) is so vast that exhaustively searching them is impractical. The search process can be improved through the use of heuristics—rules that are specific to a given problem and can therefore help guide the search. For example, a chess heuristic might indicate that when a move results in checkmate, there is no point in examining alternate moves.

Robotics

Another area of computer science that has found wide practical use is robotics—the design and development of computer controlled mechanical devices. Robots range in complexity from toys to automated factory assembly lines, and relieve humans from tedious, repetitive, or dangerous tasks. Robots are also employed where requirements of speed, precision, consistency, or cleanliness exceed what humans can accomplish. Roboticists—scientists involved in the field of robotics—study the many aspects of controlling robots. These aspects include modeling the robot’s physical properties, modeling its environment, planning its actions, directing its mechanisms efficiently, using sensors to provide feedback to the controlling program, and ensuring the safety of its behavior. They also study ways of simplifying the creation of control programs. One area of research seeks to provide robots with more of the dexterity and adaptability of humans, and is closely associated with AI.

Human-computer interfacing

Human-computer interfaces provide the means for people to use computers. An example of a human-computer interface is the keyboard, which lets humans enter commands into a computer and enter text into a specific application. The diversity of research into human-computer interfacing corresponds to the diversity of computer users and applications. However, a unifying theme is the development of better interfaces and experimental evaluation of their effectiveness. Examples include improving computer access for people with disabilities, simplifying program use, developing three-dimensional input and output devices for virtual reality, improving handwriting and speech recognition, and developing heads-up displays for aircraft instruments in which critical information such as speed, altitude, and heading are displayed on a screen in front of the pilot’s window. One area of research, called visualization, is concerned with graphically presenting large amounts of data so that people can comprehend its key properties.

Connection of computer science to other disciplines

Because computer science grew out of mathematics and electrical engineering, it retains many close connections to those disciplines. Theoretical computer science draws many of its approaches from mathematics and logic. Research in numerical computation overlaps with mathematics research in numerical analysis. Computer architects work closely with the electrical engineers who design the circuits of a computer.

Beyond these historical connections, there are strong ties between AI research and psychology, neurophysiology, and linguistics. Human-computer interface research also has connections with psychology. Roboticists work with both mechanical engineers and physiologists in designing new robots.

Computer science also has indirect relationships with virtually all disciplines that use computers. Applications developed in other fields often involve collaboration with computer scientists, who contribute their knowledge of algorithms, data structures, software engineering, and existing technology. In return, the computer scientists have the opportunity to observe novel applications of computers, from which they gain a deeper insight into their use. These relationships make computer science a highly interdisciplinary field of study.

E-MAIL

E-Mail, in computer science, abbreviation of the term electronic mail, method of transmitting data or text files from one computer to another over an intranet or the Internet. E-mail enables computer users to send messages and data quickly through a local area network or beyond through a nationwide or worldwide communication network. E-mail came into widespread use in the 1990s and has become a major development in business and personal communications.

E-mail users create and send messages from individual computers using commercial e-mail programs or mail-user agents (MUAs). Most of these programs have a text editor for composing messages. The user sends a message to one or more recipients by specifying destination addresses. When a user sends an e-mail message to several recipients at once, it is sometimes called broadcasting.

The address of an e-mail message includes the source and destination of the message. Different addressing conventions are used depending upon the e-mail destination. An interoffice message distributed over an intranet, or internal computer network, may have a simple scheme, such as the employee’s name, for the e-mail address. E-mail messages sent outside of an intranet are addressed according to the following convention: The first part of the address contains the user’s name, followed by the symbol @, the domain name, the institution’s or organization’s name, and finally the country name.

A typical e-mail address might be [email protected]. In this example sally is the user’s name, abc is the domain name—the specific company, organization, or institution that the e-mail message is sent to or from, and the suffix com indicates the type of organization that abc belongs to—com for commercial, org for organization, edu for educational, mil for military, and gov for governmental. An e-mail message that originates outside the United States or is sent from the United States to other countries has a supplementary suffix that indicates the country of origin or destination. Examples include uk for the United Kingdom, fr for France, and au for Australia.

E-mail data travels from the sender’s computer to a network tool called a message transfer agent (MTA) that, depending on the address, either delivers the message within that network of computers or sends it to another MTA for distribution over the Internet. The data file is eventually delivered to the private mailbox of the recipient, who retrieves and reads it using an e-mail program or MUA. The recipient may delete the message, store it, reply to it, or forward it to others.

Modems are important devices that have allowed for the use of e-mail beyond local area networks. Modems convert a computer’s binary language into an analog signal and transmit the signal over ordinary telephone lines. Modems may be used to send e-mail messages to any destination in the world that has modems and computers able to receive messages.

E-mail messages display technical information called headers and footers above and below the main message body. In part, headers and footers record the sender’s and recipient’s names and e-mail addresses, the times and dates of message transmission and receipt, and the subject of the message.

In addition to the plain text contained in the body of regular e-mail messages, an increasing number of e-mail programs allow the user to send separate files attached to e-mail transmissions. This allows the user to append large text- or graphics-based files to e-mail messages.

E-mail has had a great impact on the amount of information sent worldwide. It has become an important method of transmitting information previously relayed via regular mail, telephone, courier, fax, television, and radio.

WINDOWS

Windows, in computer science, personal computer operating system sold by Microsoft Corporation that allows users to enter commands with a point-and-click device, such as a mouse, instead of a keyboard. An operating system is a set of programs that control the basic functions of a computer. The Windows operating system provides users with a graphical user interface (GUI), which allows them to manipulate small pictures, called icons, on the computer screen to issue commands. Windows is the most widely used operating system in the world. It is an extension of and replacement for Microsoft’s Disk Operating System (MS-DOS).

The Windows GUI is designed to be a natural, or intuitive, work environment for the user. With Windows, the user can move a cursor around on the computer screen with a mouse. By pointing the cursor at icons and clicking buttons on the mouse, the user can issue commands to the computer to perform an action, such as starting a program, accessing a data file, or copying a data file. Other commands can be reached through pull-down or click-on menu items. The computer displays the active area in which the user is working as a window on the computer screen. The currently active window may overlap with other previously active windows that remain open on the screen. This type of GUI is said to include WIMP features: windows, icons, menus, and pointing device (such as a mouse).

Computer scientists at the Xerox Corporation’s Palo Alto Research Center (PARC) invented the GUI concept in the early 1970s, but this innovation was not an immediate commercial success. In 1983 Apple Computer featured a GUI in its Lisa computer. This GUI was updated and improved in its Macintosh computer, introduced in 1984.

Microsoft began its development of a GUI in 1983 as an extension of its MS-DOS operating system. Microsoft’s Windows version 1.0 first appeared in 1985. In this version, the windows were tiled, or presented next to each other rather than overlapping. Windows version 2.0, introduced in 1987, was designed to resemble IBM’s OS/2 Presentation Manager, another GUI operating system. Windows version 2.0 included the overlapping window feature. The more powerful version 3.0 of Windows, introduced in 1990, and subsequent versions 3.1 and 3.11 rapidly made Windows the market leader in operating systems for personal computers, in part because it was prepackaged on new personal computers. It also became the favored platform for software development.

In 1993 Microsoft introduced Windows NT (New Technology). The Windows NT operating system offers 32-bit multitasking, which gives a computer the ability to run several programs simultaneously, or in parallel, at high speed. This operating system competes with IBM’s OS/2 as a platform for the intensive, high-end, networked computing environments found in many businesses.

In 1995 Microsoft released a new version of Windows for personal computers called Windows 95. Windows 95 had a sleeker and simpler GUI than previous versions. It also offered 32-bit processing, efficient multitasking, network connections, and Internet access. Windows 98, released in 1998, improved upon Windows 95.

In 1996 Microsoft debuted Windows CE, a scaled-down version of the Microsoft Windows platform designed for use with handheld personal computers. Windows 2000, released at the end of 1999, combined Windows NT technology with the Windows 98 graphical user interface.

Other popular operating systems include the Macintosh System (Mac OS) from Apple Computer, Inc., OS/2 Warp from IBM, and UNIX and its variations, such as Linux.

Перевод

АЛГЕБРА

Введение

Алгебра, раздел математики, в котором символы используются для представления основных арифметических операций. Как и в арифметике, основные операции алгебры являются сложение, вычитание, умножение, деление и извлечение корней. Арифметика, однако, не может обобщать математические отношения, такие как теорема Пифагора, которая гласит, что сумма квадратов сторон любого прямоугольного треугольника также квадрат стороны. Арифметика может только приводить примеры этих отношений (например, 3, 4, и 5, где ). Но алгебра может сделать общее высказывание, которое удовлетворяет условиям теоремы: . Любое число, умноженное само на себя, называется квадратом и обозначается индексом 2. Например, 3 × 3 обозначается 3²; аналогично, a×a эквивалентно a² (см. экспонента; степень; корень).
Классическая алгебра, которая связана с решением уравнений, использует символы вместо конкретных цифр и использует арифметические операции, чтобы установить способы обработки символов (см. уравнения, уравнения, теория). Современная алгебра произошла из классической алгебры, увеличивая свое внимание на структуры в математике. Математики рассматривают современную алгебру как множество объектов с правилами для подключения или в связи с ними. Таким образом, в самом общем виде, алгебра может быть описана как язык математики.

История

История алгебры началось в Древнем Египте и Вавилоне, где люди научились решать линейные (ax = b) и квадратные (ax² + bx = c) уравнения, а также неопределенные уравнения, такие как x² + y² = z², когда участвует несколько неизвестных. Древние вавилоняне решали произвольные квадратные уравнения, практически теми же самыми процедурами, которые изучаются сегодня. Они также могли решить некоторые неопределенные уравнения.
Александрийские математики Герон и Диофанта продолжили традиции Египта и Вавилона, но книга Диофанта «Арифметика» находится на гораздо более высоком уровне и дает много удивительных решений сложных неопределенных уравнений. Это древнее знание решений уравнений в свою очередь, нашло начало в исламском мире, где оно было известно как "наука о восстановлении и балансировки." (Арабское слово для восстановления, аль-джабру, является корнем слова алгебра.) В 9-м веке арабский математик аль-Хорезми написал одну из первых арабских алгебр, систематически изложив основные теории уравнений, с примерами и доказательствами. К концу 9 века, египетский математик Абу Камил сформулировал и доказал основные законы и тождества алгебры и решил такие сложные задачи, как отыскание х, у, z таких, что

х + y + z = 10, x² + y² = z², и хz = y².
Древние цивилизации выписывали алгебраические выражения, используя лишь иногда сокращения, но в средневековье исламские математики были способны говорить о сколь угодно высокой степени неизвестной х, и задать основу алгебры многочленов (без использования современных символов). Это включало способность умножать, делить, и находить квадратные корни многочленов, а также знание биномиальных теорем. Персидский математик, астроном и поэт Омар Хайям показал, как выразить корни кубического уравнения отрезками, полученными пересечением кривых второго порядка, но он не смог найти формулу для корней. Латинский перевод Алгебры аль-Хорезми появился в 12 веке. В начале 13-го века, великого итальянского математика Леонардо Фибоначчи получил приближенное решение кубического уравнения x³ + 2x² + cх = d. Потому что Фибоначчи ездил в исламские страны, он, вероятно, использовал арабский метод последовательных приближений.
В начале 16-го века, итальянских математики Сципион дель Ферро, Никколо Тарталья, и Джероламо Кардано решили общее кубическое уравнение в терминах констант, входящих в уравнения. Ученик Кардано, Лодовико Феррари, вскоре обнаружили точное решение уравнений четвертой степени, и, как следствие, математики в течение следующих нескольких веков пытались найти формулу для корней уравнений пятой степени или выше. В начале 19 века, однако, норвежского математика Нильс Абеля и французский математик Эварист Галуа доказали, что такой формулы не существует.
Важным событием в алгебре 16 века было введение символов для неизвестного и алгебраических степеней и операций. В результате этого развития, книга III Геометрия (1637), написанная французским философом и математиком Рене Декарт, выглядит как современный текст алгебры. Наиболее значительный вклад Декарта в математику, однако, было его открытие аналитической геометрии, которая сводит решение геометрических задач к решению алгебраических. Его геометрия также содержала основы курса по теории уравнений, в том числе его так называемое правило знаков для подсчета числа, которое Декарт называет «истинными» (положительными) и "ложными" (отрицательными) корнями уравнения. Работа продолжалась в течение 18-го века по теории уравнений, но пока в 1799 не был опубликовано доказательство, немецкий математик Карл Фридрих Гаусс, показал, что каждый многочлен уравнение имеет хотя бы один корень в комплексной плоскости (см. номер: комплексные числа).
К тому времени Гаусса, алгебра вступила в современную фазу. Внимание смещается с решения полиномиальных уравнений к изучения структуры абстрактных математических систем, аксиомы были основаны на поведении математических объектов, такие, как комплексные числа, которые математики встречали при изучении полиномиальных уравнений. Два примера таких систем - это группы (см. Группа) и кватернионы, которые делят некоторые свойства систем счисления, но также отклоняются от них в важных направлениях. Группы начинались как системы перестановки и комбинации корней многочленов, но они стали одним из главных объединяющих понятиями 19-го века математики. Значительный вклад в их изучение внес французские математики Галуа и Августин Коши, британский математик Артур Кэли, и норвежский математиков Нильс Абеля и Софус Ли. Кватернионы были обнаружены британским математиком и астрономом Уильям Роуэн Гамильтоном, который уточнил арифметику комплексных чисел кватернионов, в то время как комплексные числа имели вид а + bi, кватернионы имеют вид a + bi+cj+dk.
Сразу же после открытия Гамильтона, немецкий математик Герман Гресман начал исследование векторов. Несмотря на их абстрактный характер, американский физик Дж. У. Гиббса выявил в векторной алгебре, что удобна для физиков, так же Гамильтон признали практичность кватернионов. Огромное влияние этого абстрактного подхода привело Джорджа Буля написать законы мышления (1854), алгебраически рассмотрев основы логики. С того времени, современная алгебра, также называемая абстрактная алгебра, продолжала развиваться. Важные новые результаты были обнаружены, и эта тема нашла применение во всех областях математики и во многих науках.

Операции с полиномами

Производя действия над полиномами, предполагают, что основные законы арифметики чисел выполняются. В арифметике, числа использовались как множество рациональных чисел (см. номер, теории чисел). Арифметика сама по себе не может выйти за пределы этого, но алгебры и геометрии могут включать в себя как иррациональные числа, такие, как квадратный корень из 2, и комплексные числа. Множество всех рациональных и иррациональных чисел вместе составляют ряд так называемых действительных чисел.

Законы сложения

Сумма любых двух действительных чисел A1) a и b снова действительное число, обозначаемое а + b. Действительные числа замкнуты относительно операций сложения, вычитания, умножения, деления и извлечения корней, это означает, что применение любых из этих операций для действительных чисел дает величину, которая также является действительным числом.

Независимо от того, как осуществляется сложение, сумма A2. всегда будет одинаковой: (A + B) + C = A + (B + C). Это называется ассоциативный закон сложения.

Для любого действительного A3. a числа, существует такое число 0, называемое нулевым элементом относительно сложения, так, что a + 0 = 0 + а = а.

Для любого действительного A4. числа a,существует такое число (-a), называемое обратным к числу a , такое что (a) + (-а) = 0.

Независимо от того, в каком порядке осуществляется сложение, сумма A5. всегда будет одинаковая: А + B = B + А. Это называется коммутативным законом сложения.

Любой набор чисел, подчиняющихся законам A1-A4, образуют группу. Если набор также подчиняется A5, то группа называется абелевой или коммутативной.

Законы умножения

Законы, применяемые для сложения, применяются также и для умножения. Особое внимание уделяется единичному элементу умножения и обратному элементу, М3 и М4.

Произведение любых двух действительных чисел M1. a и b есть действительное число, обозначаемое А• B или AB.

Независимо от того, как члены группируются, M2. произведение будет всегда одинаковое: (АВ) С = А(BC). Это называется ассоциативный закон умножения.

Для любого действительного числа M3., существует число один (1), называемое единичным элементом умножения, такое, что a(1) = 1 (а) = а.

Для любого ненулевого действительного числа a M4., существует число (a^-1), или (1 / а), называемое обратным, такое, что a(a^-1) = (a^-1)a = 1.

Независимо от того, в каком порядке осуществляется умножение, произведение M5. всегда будет одинаковое: АВ = ВА. Это называется коммутативной закон умножения.

Любой набор элементов, подчиняющийся этим пяти законам, называется абелевой или коммутативной группой. Множество всех действительных чисел, кроме нуля (так как деление на ноль недопустимо), образует такую коммутативную группу относительно умножения.

Распределительные законы

Другим важным свойством для множества действительных чисел является связь сложения и умножения, которое отображается в двух распределительных законах:

D1. (B + C) = AB + AC

D2. (B + C) = ВА + СА

Любой набор элементов, для которого определены две операции (например, сложение и умножение), и который подчиняется всем законам A1- A5, M1-M5 и распределительным законам D1 и D2 , представляет собой поле.

ЧИСЛА

Введение

Цифры, знаки или символы используются для графического представления чисел. Ранние формы представления чисел были просто прямые линии, вертикальные или горизонтальные, каждая линия соответствовала числу 1. Такая система была неудобной при работе с большими числами, и в 3400 до н.э. в Египте и в 3000 до н.э. в Месопотамии был принят специальный символ для числа 10. Помимо этого двойное число дало возможность выразить число 11 двумя символами вместо 11 отдельных символов и число 99 18 символами вместо 99 отдельных символов. Позднее системы счисления представлялись дополнительными символами, для чисел между 1 и 10, обычно либо 4 или 5 и дополнительные символы для чисел больше 10. В Вавилоне клинописные представления цифр, использовались для 1, также для 60 и степени 60; значение числа было определялось по контексту. Это был логическим соглашением с математической точки зрения, потому что 60⁰ = 1, 60¹ = 60 и 60² = 3600. Египетская иероглифическая система использовала специальные символы для 10, 100, 1000 и 10 000.

Древние греки имели две параллельные системы счисления. Ранняя из них была основана на начальных буквах названия чисел: число 5 обозначалось как буква pi; 10 - буква дельта; 100 - античная форма буквы H; 1000 – буква хи; и 10 000 – буква мю. Поздняя система, которая впервые была представлена в III века до н.э., заняла все буквы греческого алфавита плюс три буквы, заимствованные из финикийского алфавита в качестве символов. Первые девять буквы алфавита были использованы для чисел от 1 до 9, второй девять букв для десятков от 10 до 90 и последние девять букв для сотен от 100 до 900. Тысячи указывались, поместив черту слева от соответствующей цифры, и десятки тысяч, поместив соответствующую букву за буквой М. Поздняя греческая система имела преимущество в том, что большое число может быть выражено минимальным количеством символов, но он имела недостаток, требуя от пользователя запомнить в общей сложности 27 символов.

Римские цифры

Система счисления, созданная римлянами выражала все числа от 1 до 1 000 000, в общей сложности, используя семь символов: I для 1, V для 5, X для 10, L для 50, C для 100, D для 500 и М для 1000. Римские числа читались слева направо. Символы, представляющие огромное количество размещаются слева; справа от них размещали символы, представляющие крупные величины и так далее. Символы, обычно записывались вместе. К примеру, LX = 60 и MMCIII = 2103. Когда цифры меньше цифры справа, то число слева следует вычесть из числа справа. К примеру, XIV = 14 и IX = 9. M представляет 1000000 — небольшая черта, расположенная над числом умножает его на 1000. Таким образом, теоретически это возможно, с помощью бесконечного количества черт, чтобы выразить числа от 1 до бесконечности. Однако, на практике, обычно используется одна черта; две используются редко, и более чем две почти никогда не используются. Римские цифры все еще используются сегодня, более чем 2000 лет после их появления. Римская система имеет один недостаток, в том, что не подходит для быстрых письменных вычислений.

Арабские цифры

Общая система представления чисел, которая используется в большинстве частей мира сегодня, является арабская система. Эта система была впервые разработана индусами и стала использоваться в III веке до н.э. в Индии. В то время цифры 1, 4 и 6 были написаны в той же форме, которая используется сегодня. Вероятно, индуистская система счисления была введена в арабском мире в 7 или 8 веках н.э. В 976 г. н. э. первые записи этой системы используются в Европе.

Важным новшеством в арабской системе было использование позиционных обозначений, в которой индивидуальный номер символа принимал различные значения согласно их позиции при записи. Позиционное представление дало возможность использовать символ для нуля. С помощью нуля можно различать 11, 101 и 1001 без использования дополнительных символов, и все числа можно выразить используя десять символов, цифры от 1 до 9 плюс 0. Позиционное представление также значительно упростило все формы письменного численного расчета.

АКСИОМА

Аксиома, в логике и математике, основной принцип, который предполагает истину без доказательства. Использование аксиом в математике пошло от древних греков, наиболее вероятно с 5 века до н.э. и представляет собой начало чистой математики, как это известно сегодня. Примеры аксиом следующие: «Высказывание не может быть правдой и ложью одновременно» (принцип противоречия); «Если к равенству добавить равенство,то получим сумму равенств»; «Все целое больше, чем любая из его частей». Логика и чистая математика начинаются с таких недоказанных предположений, из которых выводят другие предложения (теоремы). Эта процедура необходима во избежание округлости, или бесконечной регрессии в рассуждениях. Аксиомы в любой системы должны быть согласованы друг с другом, то есть, они не должны приводить к противоречию. Они должны быть независимыми в том смысле, что они не могут быть получены одна из другой. Они также должны быть малочисленны. Аксиом иногда истолковывались как самоочевидные истины. Настоящая тенденция - избежать этой претензии и просто принять, что аксиома предполагает правду без доказательства в системе, частью которой она является.

Термины аксиома и постулат часто используются как синонимы. Иногда слово аксиома использовалось для обозначения основных принципов, которые считаются при помощи дедуктивных систем, и термин постулат использовался для объяснения первых принципов, характерных для конкретной системы, такие как евклидова геометрия. Нечасто слово аксиома используется для обозначения первых принципов в логике, и термин постулат используется для обозначения первых принципов в области математики.

ВЕКТОР (МАТЕМАТИКА)

Вектор (математика), величина, имеющая размер и направление. Например, единичная величина или скаляр, примером может быть расстояние в 6 км; векторная величина может быть представлена как направление 6 км на север. Векторы обычно представляются в виде направленных линейных сегментов, такие как на рисунке ниже; длина линии сегмента является мерой векторной величины, и ее направление то же самое, что и вектор.

Простейшее использование векторов и вычислений с помощью векторов показано на рисунке, на котором изображена лодка, двигающаяся через поток. Вектор a или , указывает движения лодки в течение заданного интервала времени, если это было движение в стоячей воде; вектор b или , показывает движение по течению за тот же период времени. Фактический путь путешествия лодка под влиянием собственного поступательного движения и течения, представимого вектором c или . С помощью векторов любой тип задачи, связанный с движением объекта, на который действует несколько сил, может быть решен графически.

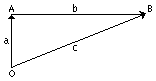
Этот метод решения задач, известный как сложение векторов, выполняется следующим образом. Вектор, представляющий одну силу, рисуют от начала O в соответствующем направлении. Длина вектора измеряется согласно любой удобной произвольной шкале, например, в сантиметрах или километрах. На рисунке скорость движения на север была 2,2 км/ч, время - 1 час, и масштаб равен 1 см:1 км. Таким образом, линия рисуется как 2,2 см, что эквивалентно 2,2 км. Текущая скорость 6 км/ч представлена вектором , длина которого 6 см, указывает расстояние 6 км, которое проехали за 1 ч. Этот второй вектор рисуется с начала в конец вектора a в направлении, параллельном течению. Точка B в конце второго вектора представляет фактическое положение лодки в конце 1 часа поездки, и фактическое расстояние путешествия представлено (в данном случае, около 6,4 км) вектором c или .

Задачи на сложение и вычитание векторов, могут быть легко решены графическими методами и также могут быть рассчитаны с помощью тригонометрии. Этот тип вычислений является полезным в решении задач навигации и движения также как и в механике и других областях физики. В современной математике вектор считается упорядоченным набором величин с соответствующими правилами манипуляции. Векторный анализ, алгебра, геометрия и вычисление векторных величин применяют в прикладной математики каждой области науки и техники.

ПОСЛЕДОВАТЕЛЬНОСТЬ И РЯДЫ

Последовательность и ряды, в математике, упорядоченная последовательность чисел или других величин , для которых известна сумма, соответственно.

Последовательность представляют как a₁, a₂,...,а_n,... a_s число или величина определенная или нет; a₁ — первый член, a₂ второй член, и так далее. Если выражение имеет последний член, то последовательность конечна; иначе бесконечна. Последовательности существует или определена, если определен n-член, для любого положительного целого числа n; это правило может быть дано как формула для n-члена. Например, целые положительные числа из ряда натуральных чисел, формируют бесконечную последовательность; эта последовательность определяется по формуле a_n= n. Формула a_n= n² определяет последовательность 1, 4, 9, 16,... Правило, начиная с 0, 1, а затем каждый последующий член есть сумма двух предшествующих членов, определяет последовательность 0, 1, 1, 2, 3, 5, 8, 13,...; данная последовательность известна как последовательность Фибоначчи.

Важные типы последовательностей включают арифметические последовательности (также известна как арифметическая прогрессия), в которых разница между членами является постоянной, и геометрические последовательности (также известные как геометрические прогрессии), в которых отношение членов является постоянным. Примеры возникают, когда вложена сумма денег. Если деньги вкладываются под 8 процентов, то через n лет первоначальная сумма в P долларов вырастает до = P + n × (0,08) P долларов. Затем (0.08)P долларов добавляется каждый год, сумма в виде арифметической прогрессии. Если проценты вместо этого смешивают, сумма последовательности формирует геометрическую прогрессию, g_n = P_n × (1.08). В обоих этих случаях, очевидно, что и g_n в конечном итоге становится больше, чем любое целое число N, каким бы большим не было N.

Члены последовательности, однако, не всегда возрастают без предела. К примеру, когда n увеличивается, последовательность = 1/n стремится к 0 как к предельному значению и bn = A + B/n стремится к а. В любом таком случае, существует некоторое конечное число L , что для любой погрешности е, существует значение последовательности, которая принадлежит е-окрестности, при этом е принадлежит L. Например, в случае последовательность 2 + (-1)ⁿ/2n, L = 2. Даже если e является очень малым, как 1/10 000, можно увидеть, что, если n — больше, чем 5000, все значения n находятся в пределах е-окрестности 2. Число L называется предел последовательности, хотя некоторые члены последовательности могут быть больше или меньше, чем L, члены приближаются все ближе и ближе к L. Когда последовательность имеет предел L,говорят что последовательность сходится к L. Для последовательности a_n, например, это записывается как lim a_n = L, который читается как «предел a_n, при n стремящейся к бесконечности есть L.»

Члены ряда относятся к указанной сумме, a₁ + a₂ +...+а_n или a₁ + a₂ +... + а_n +.... Ряд является конечным или бесконечным, в зависимости от того, является ли соответствующая последовательность членов конечной или бесконечной.

Последовательности s₁ = a₁, s₂ = a₁ + a₂, s = a₁ + a₂+ a₃..., s_n = a₁ + a₂ +... +..., называется последовательность частичных ряда a₁ + a₂ +...+а_n Ряд сходится или расходится, когда последовательность частичных сумм сходится или расходится. Ряды с постоянными членами, такие, в которых все члены числа; ряд функциональный, в котором члены ряда – функции с одной или несколькими переменными. В частности, ряд степенной a₀ + a₁(x - c) + a₂(x - c)² + ... + a_n(x - c)ⁿ + ..., в котором c и а_s являются константами. В случае степенного ряда, задача заключается в том, чтобы описать значения, к которым сходится x. Если ряд сходится к некоторому x, то ряд из всех x, к которым ряд сходится, состоит из точки или некоторого замкнутого интервала. Основа теории сходимости была разработана французским математиком Коши, Огюстеном Луи в 1820-х.

Теория и применение бесконечных рядов важна практически в каждом отрасли чистой и прикладной математики.

АРХИТЕКТУРА (ИНФОРМАТИКА)

Введение

Архитектура (информатика), общий термин, относящийся ко всей структуре или части компьютерной системы. Этот термин охватывает проектирование системного программного обеспечения, такой как, операционная система (программа, которая управляет компьютером), а также как относится сочетание аппаратного и основного программного обеспечения, которое связывает машины в компьютерной сети. Компьютерная архитектура относится ко всей структуре и к деталям, которые необходимы для создания функциональности. Таким образом, компьютерная архитектура охватывает компьютерные системы, микропроцессоры, схемы и системные программы. Обычно термин не относится к прикладным программам, таким как электронные таблицы или текстовый редактор, которые необходимы для выполнения задач, но не для того, чтобы сделать систему работающей.

Элементы проектирования

В разработке компьютерной системы, архитекторы рассматривают пять основных элементов, которые составляют оборудование системы: модуль арифметики/логики, модуль управления, памяти, ввода и вывода. Модуль арифметики/логики выполняет арифметику и сравнение чисел. Модуль управления направляет команды компьютера, взяв инструкции пользователя и превращая их в электрические сигналы, которые понимают компьютерные схемы. Сочетание модуля арифметики/логики и модуля управления называется центральным процессором (CPU). Память хранит команды и данные. Входные и выходные секции позволяют компьютеру получать и отправлять данные, соответственно.

Различные аппаратные архитектуры необходимы из-за специализированных потребностей систем и пользователей. Одному пользователю нужна система для отображения графики очень быстро, хотя другая система может быть оптимизирована для поиска по базе данных или для сохранения заряда батареи в ноутбуке.

Помимо аппаратного проектирования, архитекторы должны учитывать, какое программное обеспечение будет работать с системой. Программное обеспечение, такие, как языки программирования и операционные системы, делает детали аппаратной архитектуры невидимыми для пользователя. Например, компьютеры, использующие операционную систему UNIX или язык программирования C, могут появиться с одной и той же точки зрения пользователя, хотя они используют различные аппаратные архитектуры.

Архитектура обработки

Когда компьютер выполняет команду, он проходит через пять шагов. Во-первых, модуль управления извлекает инструкция из памяти — например, инструкция для сложения двух чисел. Во-вторых, модуль управления декодирует инструкции в электронные сигналы, которые управляют компьютером. В-третьих, модуль управления извлекает данные (два номера). В-четвертых, модуль арифметики/логики выполняет конкретные операции (сложение двух чисел). В-пятых, модуль управления сохраняет результат (сумма двух чисел).

Первые компьютеры использовали только простые инструкции, потому что стоимость электроники, способной вести сложные инструкции была высокой. Как эта стоимость в 1960-х годах сократилась, стали возможными более сложные инструкции. Сложные инструкции (инструкции, которые определяют несколько операций) могут сэкономить время, потому что они делают ненужным для компьютера получение дополнительных команд. Например, если семь операций объединяются в одной инструкции, то шесть шагов команд исключаются, и компьютер тратит меньше времени на обработку этой команды. Компьютеры, которые объединяют несколько инструкций в одну операцию, называются компьютерами со сложным набором команд (CISC).

Однако большинство программ не часто используют сложные инструкции, но состоят главным образом из простых инструкций. Когда эти простые инструкции выполняются на CISC архитектурах, они замедляют обработку, поскольку каждая инструкция — будь то простая или сложная — занимает больше времени для декодирования в CISC-архитектурах. Альтернативная стратегия является возвращением к конструкциям, которые используют только простые наборы инструкций, наборы одно-операционных команд и делает наиболее часто используемые операции быстрее, с тем, чтобы повысить общую производительность. Компьютеры, которые следуют этой конструкции, называются компьютерами с сокращенным набором команд (RISC).

RISC конструкции особенно быстры в численных вычислениях, необходимых в науке, графике и инженерных приложений. CISC конструкции обычно используются для нечисленных вычислений, потому что они предоставляют специальные наборы инструкций для обработки символьных данных, таких как текст, в программе Word. Специализированные архитектуры CISC, называют цифровые сигнальные процессоры, необходимые для ускорения обработки цифровых аудио и видео сигналов.

Открытые и закрытые архитектуры

Процессор компьютера соединяет память и внешний мир с помощью открытой или закрытой архитектуры. Открытая архитектура может быть расширена после того, как построена система, как правило, добавляя дополнительные схемы, такие, как новый микропроцессорный компьютер, подключенный к основной системе. Спецификации схемы предаются гласности, позволяя другим компаниям производить эти продукты.

Закрытые архитектуры, как правило, работают в специализированных компьютерах, которые не потребует расширения — например, компьютеры, которые управляют микроволновыми печами. Некоторые изготовители компьютеров использовали закрытые архитектуры, так что их клиенты могут приобрести расширенные схемы только от них. Это позволяет производителю взимать больше и уменьшает возможности для потребителя.

Архитектура сети

Компьютеры общаются с другими компьютерами по сети. Простейшая сеть – это сеть с прямым подключением между двумя компьютерами. Однако компьютеры также могут быть соединены через большие сети, позволяя пользователям обмениваться данными, общаться по электронной почте и совместно использовать ресурсы, такие как принтеры.

Компьютеры могут быть соединены несколькими способами. В конфигурации кольцо данные передаются по кольцу, и каждый компьютер в кольце анализирует эти данные, чтобы определить, является ли он получателем. Если данные не предназначены для конкретного компьютера, компьютер передает данные на следующий компьютер в кольце. Этот процесс повторяется до тех пор, пока данные не прибудут на их пункт назначения. Кольцевая сеть позволяет нескольким сообщениям передаваться одновременно, но так как каждое сообщение проверяется на каждом компьютере, передача данных замедляется.

В конфигурации шина компьютеры соединены через единый набор проводов, называемый шина. Один компьютер отправляет данные на другой, передавая адрес получателя и данные по шине. Все компьютеры в сети смотрят адрес одновременно, и получатель принимает данные. Сеть шина, в отличие от сети кольцо позволяет данные отправлять непосредственно с одного компьютера на другой. Однако только один компьютер в то время, может передавать данные. Остальные должны ждать, чтобы отправить свои сообщения.

В конфигурации звезда компьютеры связаны с центральным компьютером, называемым концентратор. Компьютер посылает адрес получателя и данные к концентратору, который затем связывает отправку и компьютеры получатели напрямую. Сеть звезда позволяет отправлять несколько сообщений одновременно, но она является более дорогостоящей, потому что она использует дополнительный компьютер, концентратор, который направляет данные.

Последние достижения

Одна из проблем в компьютерной архитектуре вызвана разницей между скоростью процессора и скоростью, с которой память предоставляет инструкции и данные. Современные процессоры могут обрабатывать инструкции в 3 наносекунды (3 миллиардных доли секунды). Доступ к типичной памяти, однако, занимает 100 наносекунд, и каждая инструкция может потребовать множественного доступа. Для компенсации этого различия, были разработаны новые компьютерные чипы, которые содержат небольшую память, называемая кэш, расположенная недалеко от центрального процессора. Из-за ее близости к CPU и небольшого размера кэши могут предоставить инструкции и данные быстрее, чем обычная память. Кэш-память хранит наиболее часто используемые инструкции и данные и может значительно повысить эффективность.

Хотя больше кэш-памяти может содержать больше данных, она также становится медленнее. Чтобы компенсировать, компьютерные архитекторы используют конструкции с несколькими кэшами. Конструкция помещается в маленький и быстрый кэш около CPU и дальше находят больше и медленнее кэша. Этот механизм позволяет процессору работать с наиболее часто используемыми инструкциями и данными на максимальной скорости и замедляется лишь слегка при доступе к вторичному кэшу. Использование отдельных кэшей для инструкций и данных также позволяет процессору получать данные и команды одновременно.

Еще одна стратегия для увеличения скорости и эффективности является использование нескольких модулей арифметики/логики для одновременных операций, называемый суперскалярным исполнением. В этой конструкции инструкции объединяются в группы. Модуль управления анализирует каждую группу, чтобы увидеть, содержит ли она инструкции, которые могут быть выполнены вместе. Некоторые конструкции выполняются как шесть операций одновременно. Это редко, однако, чтобы эти многие инструкции работали вместе, процессор не достигает шестикратного увеличения производительности.

Несколько компьютеров иногда объединяются в единые системы, называемые параллельными процессорами. Когда машина имеет более чем одну тысячу модулей арифметики/логики, говорят что она массивно параллельная. Такие машины используются главным образом для численных научных и инженерных расчетов. Были построены параллельные машины, содержащие шестнадцать тысяч компьютеров.

ИНФОРМАТИКА

Введение

Информатика изучает теорию, эксперимент и технику, которые формируют основу для разработки и использования компьютеров — устройств, которые автоматически обрабатывают информацию. Информатика уходит своими корнями к работе, которую выполнил английский математик Чарльз Бэббидж, который первым предложил программируемый механический калькулятор в 1837 году. До появления электронных цифровых компьютеров в 1940, информатика, как правило, не отличалась от математики и техники. С тех пор выросло количество, которые являются уникальными для дисциплины.

Развитие информатики

Ранние работы в области информатики с конца 1940-х и начала 1950-х посвящены автоматизации процесса выполнения вычислений для использования в науке и технике. Ученые и инженеры разработали теоретические модели вычислений, что позволяет им анализировать, насколько эффективны различные попытки выполнения различных расчетов. Информатика этого времени неразрывно связана с областью математики, известной как численный анализ, который рассматривает достоверность и точность вычислений.

Использование компьютеров значительно увеличилось между 1950-х и 1970-х, основное внимание информатики расширилось, за счет использования языков программирования — искусственные языки, использующие компьютерные программы и операционные системы — компьютерные программы, которые обеспечивают удобное взаимодействие между пользователем и компьютером. В это время ученые также экспериментировали с новыми приложениями и компьютерными конструкциями, созданием первых компьютерных сетей и изучение связей между вычислениями и изучениями.

В 1970-х годах производители компьютерных микросхем начали массовое производства микропроцессоров — электронных схем, которые служат в качестве центра обработки основной информации в компьютере. Эта новая технология произвела революцию в компьютерной индустрии резким снижением стоимости создания компьютеров и значительным увеличением скорости обработки. Микропроцессор дал возможность появлению персонального компьютера, что привело к взрыву в использовании компьютерных приложений. Между началом 1970-х и 1980-х гг. информатика быстро расширилась в попытке разработки новых приложений для персональных компьютеров и управления технологическими достижениями в компьютерной отрасли. Многие из более ранних исследований, которые были проделаны, вошли в общественность с помощью персональных компьютеров, большинство которых появились из раннего программного обеспечения от существующих причин и систем.

Ученые продолжают расширять границы компьютерных и информационных систем, новаторским проектированием более сложных, надежных и мощных компьютеров; позволяющим компьютерным сетям эффективно обмениваться огромным количеством информации; и ищут способы сделать так, чтобы компьютеры вели себя разумно. Так как компьютеры становятся неотъемлемой частью современного общества, ученые стремятся решать новые проблемы и изобретать лучшие методы для решения текущих проблем.

Цель информатики заключается в поиске путей для лучшего образования людей в использовании существующих компьютеров для спекулятивных исследований в технологии и подходах, которые не могут быть жизнеспособными в течение десятилетий. В основе всех этих конкретных целей лежит улучшение условий человека сегодня и в будущем с помощью улучшения использования информации.

Теория и эксперимент

Информатика сочетает в себе теорию, технику и эксперимент. В некоторых случаях ученые развивают теорию, а затем инженеры сочетают аппаратные средства и программное обеспечение, основанное на теории, и экспериментально тестируют. Примером такого ориентированного подхода является разработка новых инструментов программного обеспечения, которые затем оцениваются в фактическом использовании. В других случаях эксперименты могут привести к новой теории, такие как открытие искусственных нейронных сетей, доказывают поведение, аналогичное нейронам в головном мозге, ведущие к новой теории в нейрофизиологии.

Может показаться, что предсказуемый характер компьютеров делает эксперименты ненужными, потому что результат экспериментов должны быть известны заранее. Но, когда компьютерные системы и их взаимодействия с миром природы становятся достаточно сложны, это может привести к непредвиденному поведению. Таким образом, эксперименты и традиционные научные методы являются ключевой частью информатики.

Основные направления компьютерных наук

Компьютерные науки можно разделить на четыре основные области: разработка программного обеспечения, компьютерная архитектура (аппаратное обеспечение), взаимодействие человека с компьютером (дизайн самых эффективных способов для людей, чтобы использовать компьютеры) и искусственный интеллект (попытка сделать компьютеры, которые ведут себя разумно). Разработка программного обеспечения связана с создания компьютерных программ, которые эффективно выполняются. Архитектура компьютера связана с разработкой оптимального аппаратного обеспечения для конкретных вычислений. Области искусственного интеллекта и человеко-компьютерного взаимодействия часто включают разработку программного обеспечения и оборудования для решения конкретных проблем.

Разработка программного обеспечения

При разработке компьютерного программного обеспечения, ученые и инженеры изучают различные области и методы проектирования программного обеспечения, такие как лучшие типы языков программирования и алгоритмы (см. ниже) для использования в конкретных программах, как эффективно хранить и получать информацию и ограничения вычислений определенных комбинацией программного обеспечения компьютера. Дизайнерам программного обеспечения необходимо учитывать множество факторов при разработке программы. Часто исполнение программы в одной области должно жертвовать ради общей производительности программного обеспечения. Например, поскольку компьютеры имеют только ограниченное количество памяти, разработчики программного обеспечения должны ограничить количество функций, они включают в программу так, что они не потребуют больше памяти, чем система, в которой они используются.

Инженерия программного обеспечения представляет собой область разработки программного обеспечения, в которой ученые и инженеры изучают методы и инструменты, которые способствуют эффективному развитию корректных, достоверных и устойчивых компьютерных программ. Исследования в этой отрасли информатики рассматривают все этапы жизненного цикла программного обеспечения, который начинается с формальной проблемы спецификации и прогрессирует до проектирования решения, его реализация как программы, тестирование программы и обслуживание. Разработчики программного обеспечения создают программные инструменты и коллекции инструментов под названием среда программирования для улучшения процесса развития. Например, средства могут помочь управлять многими компонентами в большой программе, которая написана группой программистов.

Алгоритмы и структуры данных являются строительными блоками компьютерных программ. Алгоритм является точной пошаговой процедурой для решения проблемы за конечное время и с использованием конечного количества памяти. Стандартные алгоритмы включают поиск коллекции данных, сортировки данных и численных операций, таких как умножение матриц. Структуры данных - шаблоны для организации информации и часто представляют собой отношения между значениями данных. Некоторые общие структуры данных называются списки, массивы, записи, стеки, очереди и деревья.

Ученые продолжают разрабатывать новые алгоритмы и структуры данных для решения новых проблем и повышения эффективности существующих программ. Одна область теоретических исследований называется алгоритмической сложностью. Ученые в этой области стремятся разработать методы для определения присущей эффективности алгоритмов в отношении друг друга. Еще одна область теоретических исследований под названием теория вычислимости стремится определить ограниченность, присущую вычислениям.

Разработчики программного обеспечения используют языки программирования для взаимодействия алгоритмов на компьютер. Естественные языки, такие как английский, являются неоднозначными — это означает, что их грамматические структуры и словарь можно интерпретировать различными способами — поэтому они не подходят для программирования. Вместо этого используется простой и однозначный искусственный язык. Ученые изучают способы сделать языки программирования более выразительными, тем самым упрощая программирование и сокращая ошибки. Программа, написанная на языке программирования, должна быть переведены на машинный язык (фактические инструкции, которым следует компьютер). Ученые также разрабатывают лучший перевод алгоритмов, которые производят более эффективные программы машинного языка.

Базы данных и поиск информации соотносят области исследования. База данных — это организованный набор информации, хранящейся в компьютере, например учетные данные клиентов компании. Ученые пытаются сделать проще для пользователей доступ к базам данных, предотвратить доступ неавторизованных пользователей и улучшить скорость доступа. Они также заинтересованы в развитии методов сжатия данных, так как одинаковый объем памяти может хранить больше. Базы данных иногда распространяются на несколько компьютеров, использующих обновление данных одновременно, что может привести к несогласованности хранимой информации. Для решения этой проблемы, ученые также изучают способы предотвращения несогласованности без снижения скорости доступа.

Поиска информации связан с хранением всех данных в коллекции, которые организованы не четко, например, файл газетных статей. Ученые разрабатывают алгоритмы для создания индексации данных. Как только информация индексируется, методы, разработанные для баз данных, могут использоваться для ее организованности. Интеллектуальный анализ данных — это тесно связанные поле, в котором обширная информация анализируется, чтобы определить шаблоны. Например, сбор учета продаж из продуктового магазина может определить торговый шаблоны помощи в магазине чулок для более эффективного хранения.

Операционные системы - это программы, которые управляют общим функционированием компьютера. Они предоставляют пользовательский интерфейс, место программы в памяти компьютера и заставляют его выполнять их, контролировать устройствами ввода и вывода компьютера, управлять ресурсами компьютера такими как, дисковое пространство, защищающее компьютер от несанкционированного использования и защиты хранимых данных. Ученые заинтересованы в создании операционных систем простых в использовании, более безопасных и более эффективных, путем разработки нового дизайна пользовательского интерфейса, разработки новых механизмов, которые позволяют предотвращать доступ к конфиденциальным данным, и разработки алгоритмов, которые эффективно используют время и память компьютера.

Исследование численных вычислений включает в себя разработку алгоритмов для вычислений, часто для больших наборов данных или с высокой точностью. Поскольку многие из этих вычислений могут занять дни или месяцы, чтобы выполнения, ученые заинтересованы в проведении расчетов как можно более эффективно. Они также изучают способы повышения точности вычислений, которые могут иметь такие эффекты как повышение точности прогноза погоды. Цели повышения эффективности и точности часто конфликтуют, с большей эффективностью, получаемых за счет точности и наоборот.

Символьные вычисления включает в себя программы, которые манипулируют нечисловыми символами, такие как символы, слова, рисунки, алгебраические выражения, зашифрованные данные (данные, закодированные для предотвращения несанкционированного доступа) и части структур данных, которые представляют отношения между значениями. Одно свойство, объединяющее символьные программы является, что для них часто не хватает регулярных моделей обработки, найденных во много численных вычислениях. Такие нарушения представляются ученым особо проблемными в создании теоретических моделей программной эффективности, в переводе на машинный язык программы и в указании проверки корректности поведения.

Архитектура компьютера

Архитектура компьютера является проектом и анализом новых компьютерных систем. Архитекторы изучают пути совершенствования компьютеров, путем повышения их скорости, емкости и надежности и снижением их стоимости и мощность потребления. Архитекторы разрабатывают программное и аппаратное обеспечение моделей для анализа производительности существующих и предлагаемых конструкций компьютера, а затем использование этого анализа направляется для развития новых компьютеров. Они часто участвуют в разработке новых компьютеров, потому что точность их моделей зависит от конструкции компьютерных схем. Многие архитекторы заинтересованы в развитии компьютеров, которые являются специализированными для конкретных приложений, таких как обработка изображений, обработки сигнала или управления механическими системами. Оптимизация компьютерной архитектуры для конкретных задач часто дает более высокую производительность, ниже стоимости или и то и другое.

Искусственный интеллект

При исследовании искусственного интеллекта стремятся включить компьютеры и аппараты для имитации человеческого разума и чувств обработки способности и модели поведения человека с компьютерами для улучшения нашего понимания интеллекта. Многие отрасли исследований ИИ включают машинное обучения, вывод, познание, представление знаний, решение проблем, основ рассуждения, понимания естественного языка, распознавание речи, компьютерное зрение и искусственные нейронные сети.

Ключевым методом разработки в исследовании искусственного интеллекта является указание проблем, как множество состояний, некоторые из которых являются решениями, а затем поиск решения состояний. Например, в шахматах, каждый ход создает новое состояние. Если компьютер нашел состояния в результате всех возможных последовательностей шагов, он может определить тех, кто выиграет игру. Тем не менее, число состояний, связанных со многими проблемами (такими, как возможное количество ходов, необходимых для победы в шахматы) настолько велико, что исчерпывающий поиск их нецелесообразен. Процесс поиска может быть улучшен с помощью эвристических правил, которые являются специфическими для данной задачи и поэтому может помочь вести поиск. Например, шахматы эвристически могут означать, что если ход приводит к мата, нет смысла изучать альтернативные ходы.

Робототехника

Еще одной областью компьютерных наук, которая нашла широкое практическое применение является робототехника — проектирование и разработка компьютера контролируемого механическими устройствами. Роботы, от игрушек до автоматизированных сборочных линий, освобождают людей от утомительных, повторяющихся или опасных задач. Роботы используются также, где скорость, точность, последовательность или чистоты превышает работу человека. Робототехники — ученые, участвующие в области робототехники — изучают многие аспекты управления роботами. Эти аспекты включают в себя моделирование физических свойств робота, моделирования окружающей среды, планирования своих действий, направляя свои механизмы эффективно, используя датчики для обеспечения обратной связи в программе контроля и обеспечение безопасности его поведения. Они также изучают упрощенные пути создания управляющих программ. Одна из областей исследования стремится предоставить роботам больше ловкости и адаптируемости к людям, и тесно связана с ИИ.

Взаимодействия человек - компьютер

Взаимодействие человека с компьютером предоставляет средства для людей, чтобы использовать компьютеры. Пример интерфейса человек-компьютер является клавиатура, которая позволяет людям вводить команды в компьютер и вводить текст в конкретных приложениях. Разнообразие исследований во взаимодействие человек-компьютер соответствует разнообразию компьютерных пользователей и приложений. Однако, объединяющая тема является развитие лучшего интерфейсов и экспериментальной оценки его эффективности. Примеры включают улучшение доступа к компьютеру для людей с ограниченными возможностями, упрощение использования программы, разработка трехмерных входных и выходных устройств виртуальной реальности, улучшения рукописного текста и распознавание речи, разработки быстро реагирующих дисплеев для самолетов, в которых критически важна информация, например, скорость, высота, заголовок отображается на экране перед окном пилота. Одна из областей исследования, называемая визуализацией, связана с графическим представлением большого количество данных, так что люди могут понять его ключевые свойства.

Подключение компьютерных наук к другим дисциплинам

Так как информатика выросла из математики и электротехники, она сохраняет множество тесных связей с этими дисциплинами. Теоретическая информатика берет много из математики и логики. Исследования в численных вычислениях связана с математическими исследованиями в численном анализе. Архитекторы тесно работают с инженерами-электриками, которые проектируют схемы компьютера.

Помимо этих исторических связей существуют прочные связи между исследованиями ИИ и психологии, нейрофизиологии и лингвистики. Исследования человека компьютерного взаимодействия также имеет связи с психологией. Робототехники работают с инженерами-механиками и физиологами в проектировании новых роботов.

Информатика имеет косвенное отношение к практически всем дисциплинам, которые используют компьютеры. Приложения, разработанные в других областях, часто предусматривают сотрудничество с информатиками, которые пополняют свои знание алгоритмов и структур данных, программного обеспечения, существующих технологии. В свою очередь ученые имеют возможность наблюдать за новыми применениями компьютеров, от которых они получают глубокое понимание использования. Эти отношения делают информатику высоко междисциплинарной областью исследования.

E-MAIL

E-Mail, в информатики, аббревиатура термина электронная почта, метод передачи данных или текстовых файлов с одного компьютера на другой через интранет или интернет. Электронная почта позволяет пользователям компьютеров отправлять сообщения и данные быстро через локальную сеть или за ее пределы через общенациональную или мировую коммуникационную сеть. Электронная почта получила широкое распространение в 1990-х годах и стала важным событием в деловой и личной коммуникации.

Пользователи электронной почты создают и отправляют сообщения с отдельных компьютеров, используя коммерческие почтовые программы или почтовые агенты (MUA). Большинство из этих программ имеет текстовый редактор для создания сообщений. Пользователь посылает сообщение одному или нескольким адресатам, указав адреса назначения. Когда пользователь отправляет сообщение электронной почты нескольким адресатам одновременно, это называется широковещанием.

Адрес электронной почты включает в себя источник и место назначения сообщения. Различные условные обозначения используют в зависимости от назначения электронной почты. Межведомственные сообщения распространяются через интранет или внутреннюю компьютерную сеть, могут иметь простую схему, такую ​​как имя сотрудника, адрес электронной почты. Сообщения электронной почты отправляются за пределы интрасети, рассматриваются в соответствии со следующим правилом: первая часть адреса содержит имя пользователя, а затем символ @, имя домена, учреждения или название организации, и, наконец, название страны.

Типичный адрес электронной почты может быть [email protected]. В этом примере Салли - имя пользователя, АВС доменное имя конкретной компании, организации или учреждения, которому отправляется сообщение или от кого приходит, суффикс com указывает тип организации, например ABC принадлежит к com – коммерческая организация, org – организация, edu образовательное учреждение, mil для военных, и для государственных gov. Сообщения электронной почты, что приходит за пределы Соединенных Штатов или посылается из США в другие страны, имеет дополнительный суффикс, указывающий страну происхождения или назначения. Примеры, uk для Соединенного Королевства, fr для Франции, и au для Австралии.

Данные почтовые путешествует с компьютера отправителя в сети, называется агент передачи сообщений (MTA), который, в зависимости от адреса, либо доставляет сообщение в этой сети компьютеру или передает его другому MTA для распространения через Интернет. Файл данных, в конечном счете доставляется в личный почтовый ящик получателя, который получает и читает его с помощью программы электронной почты или MUA. Получатель может удалить сообщение, сохранить его, ответить на него или переслать его другим.

Модемы важные устройства, которые позволяют использовать электронную почту за пределами локальной сети. Модемы преобразуют двоичный языка компьютера в аналоговый сигнал и передает сигнал по обычным телефонным линиям. Модемы могут быть использованы для отправки сообщений электронной почты в любую точку мира, которая имеет модем и компьютер имеет возможность получать сообщения.

Сообщения электронной почты отображают технические характеристики, называемые верхние и нижние колонтитулы, расположенные сверху и снизу основной части сообщения. В частности, заголовок и заключение содержат записи отправителя и получателя и адреса электронной почты, времени и даты передачи сообщений и получения, и тема сообщения.

В дополнение к простому тексту, содержащемуся в теле сообщения электронной почты, большее число программ электронной почты позволяют пользователям отправлять отдельные файлы, прикрепленные к электронной почте. Это позволяет пользователю добавлять большие текстовые или графические файлы к основным сообщениям электронной почты.

Электронная почта оказала большое воздействие на объем информации, передаваемой по всему миру. Это стало важным способом передачи информации, раньше все предавалось через обычную почту, телефон, курьером, факсом, телевидение и радио.

WINDOWS

Windows, в информатике, персональная операционная система, которую реализует корпорация Майкрософт, позволяющая пользователям вводить команды с устройством point-and-click, например мышь, а не клавиатура. Операционная система представляет собой набор программ, которые контролируют основные функции компьютера. Операционная система Windows предоставляет пользователям графический интерфейс пользователя (GUI), который позволяет манипулировать маленькими картинками, называемые иконки, отображающиеся на экране компьютера для выдачи команд. Windows является наиболее широко используемой операционной системой в мире. Это расширение и замены для диска операционной системы корпорации Майкрософт (MS-DOS).

Графический интерфейс Windows предназначен для естественной, или интуитивной, рабочей среды пользователя. С Windows пользователь может перемещать курсор на экране компьютера с помощью мыши. Наведение курсора мыши на значки и кликнув на мышь, пользователь может выдавать команды на компьютер для выполнения действий, например запуск программы, доступ к файлу данных или копирования файла данных. К другим командам можно добраться через пункты меню. Компьютер отображает активную область, в которой пользователь работает в окне на экране компьютера. В настоящее время активные окна могут перекрываться с другими ранее активными окнами, которые остаются открытыми. Этот тип графического интерфейса, что включает WIMP функции: windows, значки, меню и указывающие устройства (например, мышь).

Ученые из корпорации Xerox Palo Alto Research Center (PARC) изобрели концепцию GUI в начале 1970-х, но это нововведение не быстрого коммерческого успеха. В 1983 году Apple Computer применили GUI в своем компьютере Лиза. Этот графический интерфейс обновлен и улучшен в своем компьютере Macintosh, созданном в 1984 году.

Корпорация Майкрософт начала свое развитие GUI в 1983 году как расширение своей операционной системы MS-DOS. Microsoft's Windows версии 1.0 впервые появился в 1985 году. В этой версии windows были плитки, или представлены рядом друг с другом, а не дублировались. Windows версии 2.0, введена в 1987 году, был разработан для напоминания другой GUI операционной системы IBM OS/2. Windows версии 2.0 включает функцию перекрывания окон. Более мощные версии 3.0 Windows, введена в 1990 и последующие версии 3.1 и 3.11 быстро сделали Windows лидером на рынке операционных систем для персональных компьютеров, отчасти потому что она была внедрена на новые персональные компьютеры. Это также стало благоприятной платформой для разработки программного обеспечения.

В 1993 году Microsoft представил Windows NT (новые технологии). Операционная система Windows NT представляет 32-разрядных многозадачную систему, которая дает компьютеру возможность запускать несколько программ одновременно, или параллельно, на высокой скорости. Эта операционная система конкурирует с IBM OS/2 как платформа с интенсивными, высококонечными, сетевыми вычислительными средами, которые используются во многих компаниях.

В 1995 году Microsoft выпустил новую версию Windows для персональных компьютеров под названием Windows 95. Windows 95 имела компактный и простой GUI, чем предыдущие версии. Она также предложила 32-битную обработку, эффективную многозадачность, сетевые подключения и доступ в Интернет. Windows 98, выпущенный в 1998 году, улучшенная версия Windows 95.

В 1996 году Microsoft дебютировал с Windows CE, урезав версию платформы Microsoft Windows, предназначенную для использования в карманных персональных компьютерах. Windows 2000, выпущенный в конце 1999 года, объединил технологии Windows NT с графическим пользовательским интерфейсом Windows 98.

Другие популярные операционные системы Macintosh (Mac OS) от Apple Computer, Inc, OS/2 Warp от IBM и UNIX и его вариации, такие как Linux.