Тема 16. СТЕПЕННЫЕ РЯДЫ

Тема 14. СТЕПЕННЫЕ РЯДЫ

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.

1. Найти область сходимости степенного ряда: .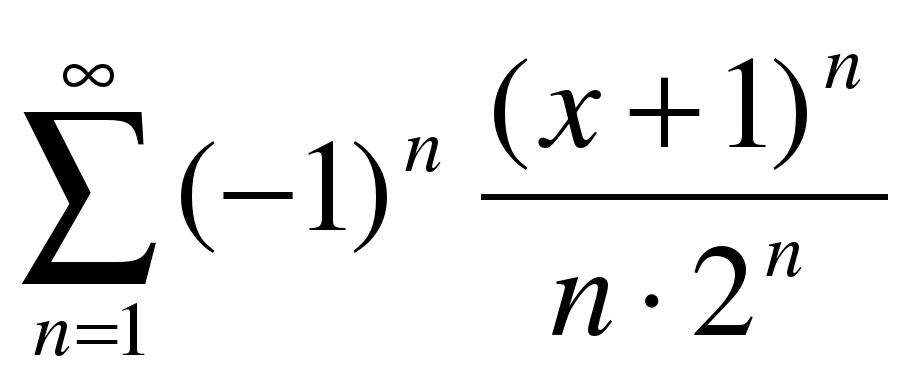

РЕШЕНИЕ:

Составим ряд из абсолютных величин членов исходного ряда:

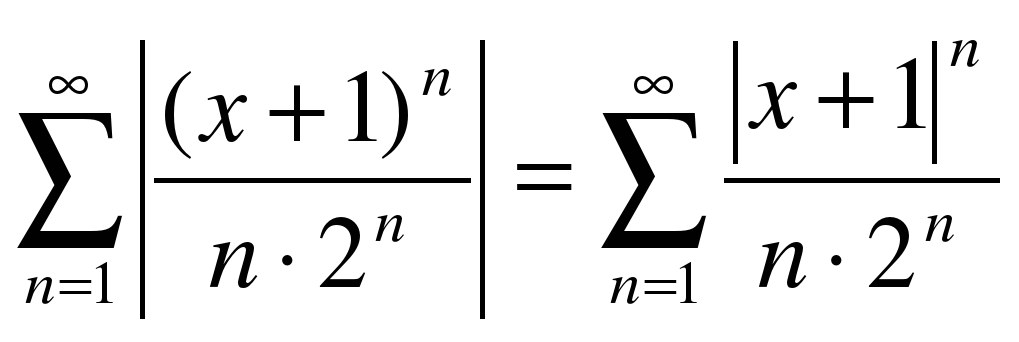
По признаку Даламбера этот ряд сходится при тех значениях 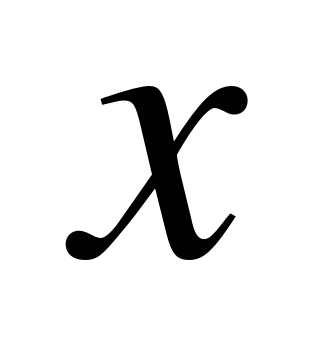, при которых выполняется условие:

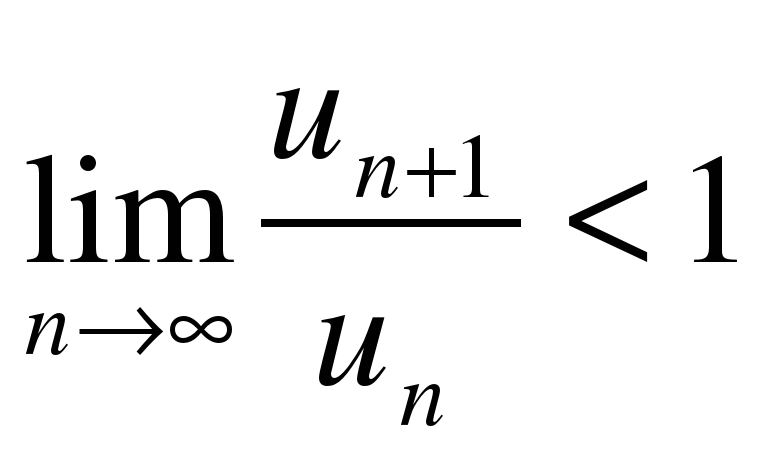
В нашем случае

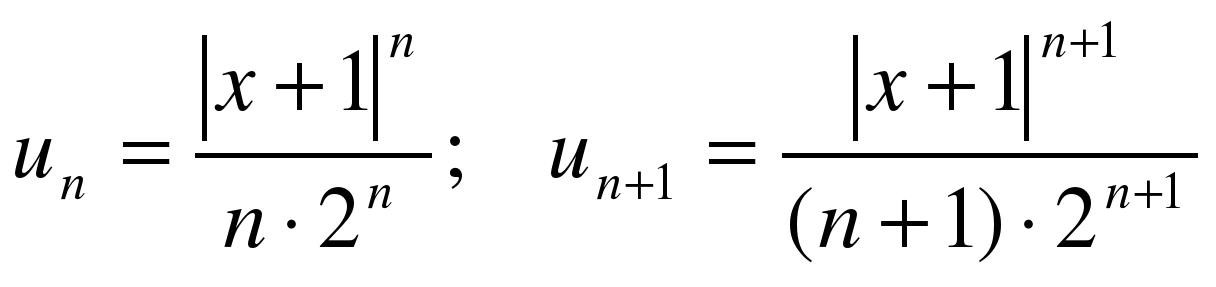
Тогда:

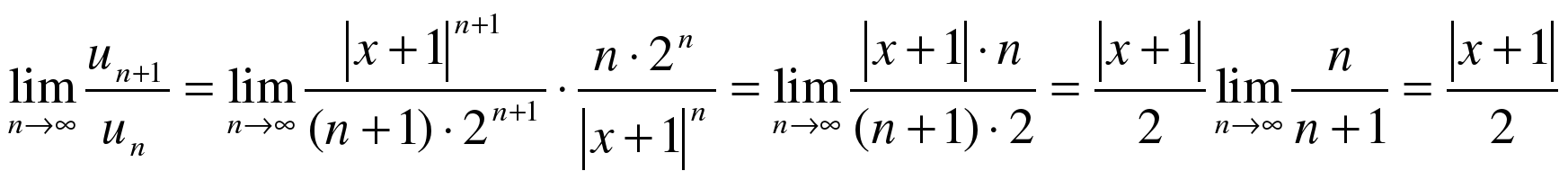
По признаку Даламбера, чтобы ряд сходился, должно выполняться условие

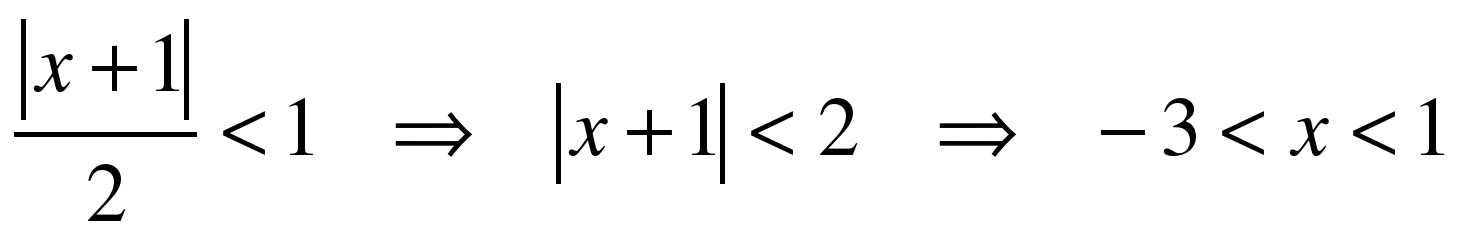
Таким образом, исходный ряд сходится на промежутке .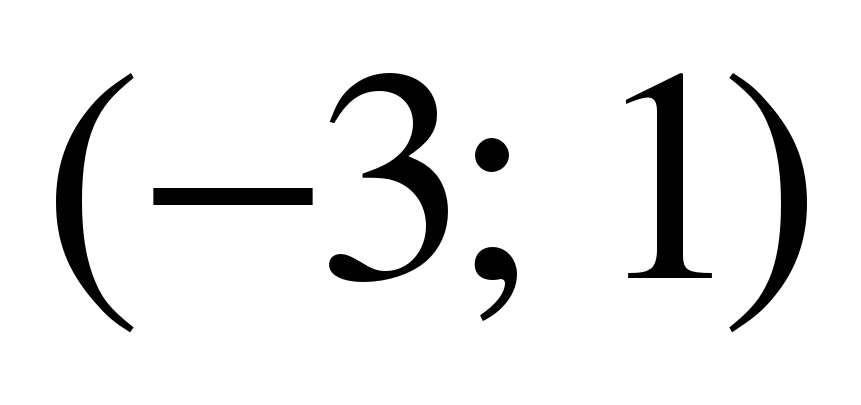

Исследуем сходимость этого ряда на концах промежутка.

При ряд принимает вид:

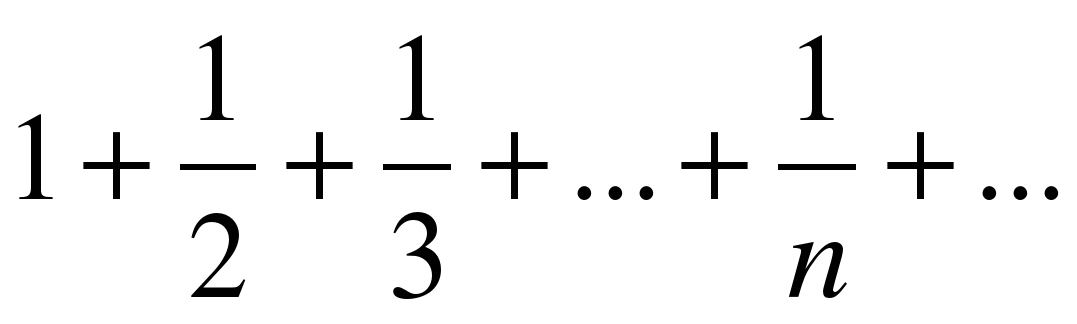
Это гармонический ряд , который расходится. Поэтому при наш ряд будет расходящимся.

При 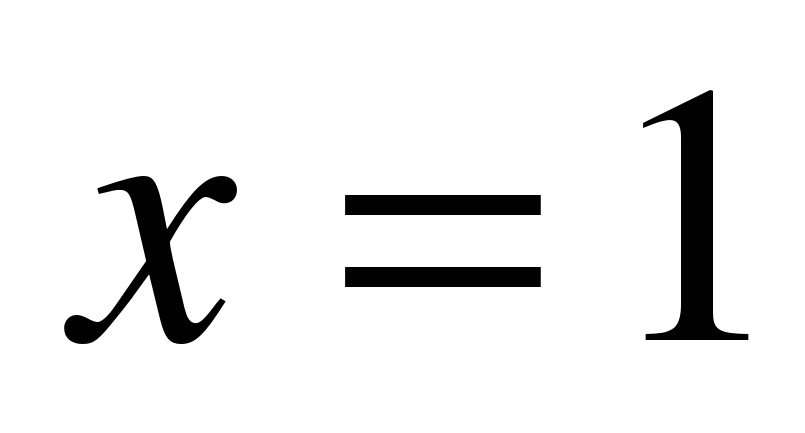ряд принимает вид:

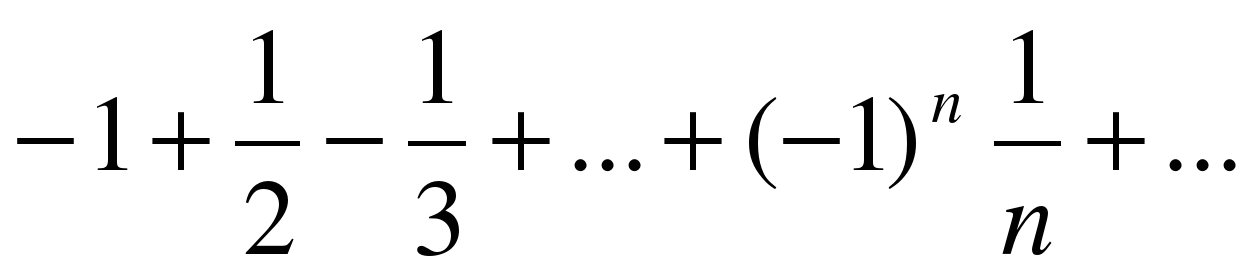
Это знакочередующийся ряд, исследуем его на абсолютную и условную сходимость.

Составляем ряд из абсолютных значений:

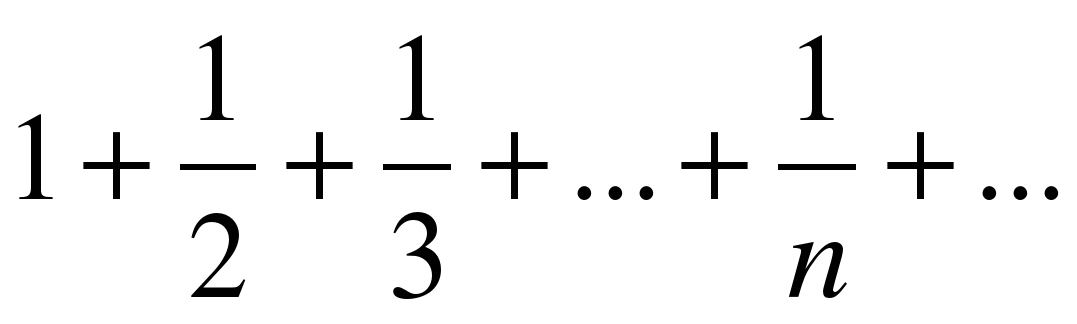
Получили опять расходящийся гармонический ряд. Следовательно абсолютной сходимости нет. Исследуем на условную сходимость по признаку Лейбница:

1.

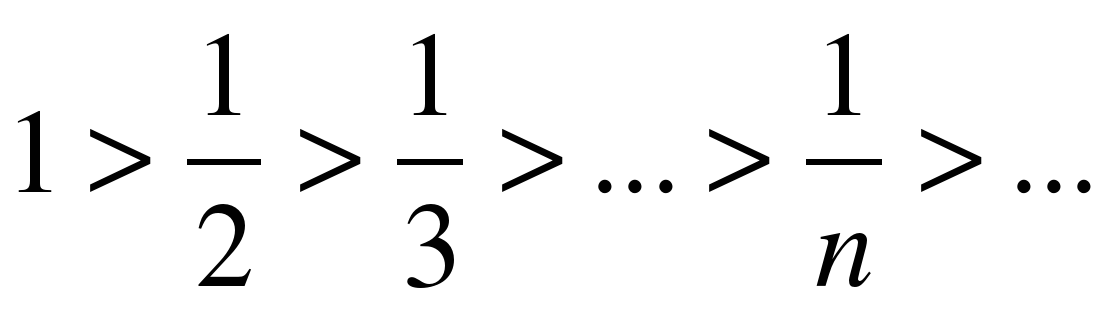
- каждый последующий член ряда меньше предыдущего, поэтому первое условие признака Лейбница выполняется.

2.

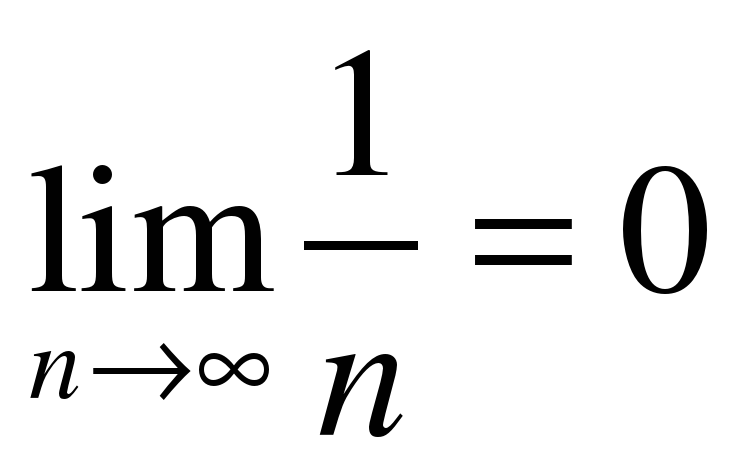
Второе условие признака Лейбница также выполняется: предел общего члена ряда равен нулю. Поэтому данный ряд будет условно сходиться.

Таким образом, область сходимости исходного ряда будет: .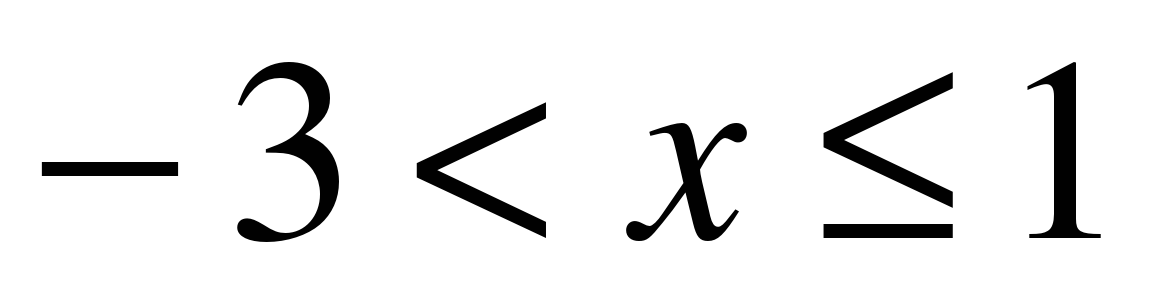

1. Разложить функцию 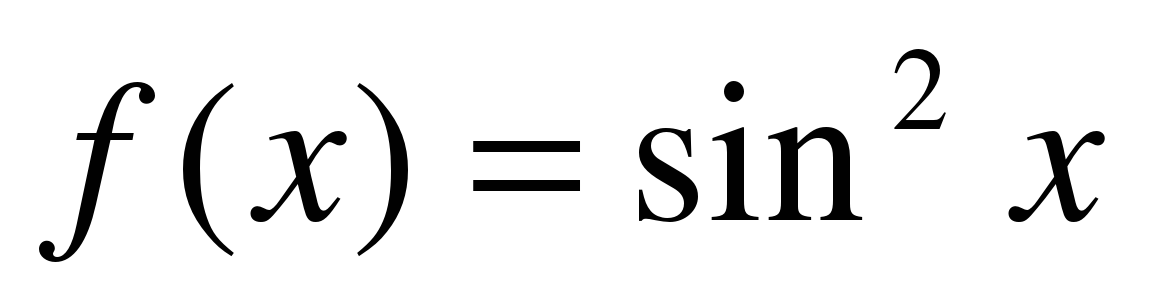в ряд Маклорена.

РЕШЕНИЕ:

1 способ.

Используем формулу непосредственного разложения функции в ряд Маклорена:

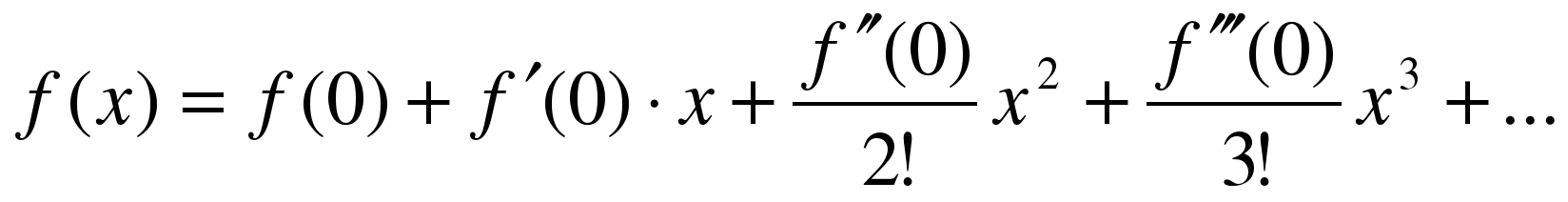
Находим производные заданной функции:

………………

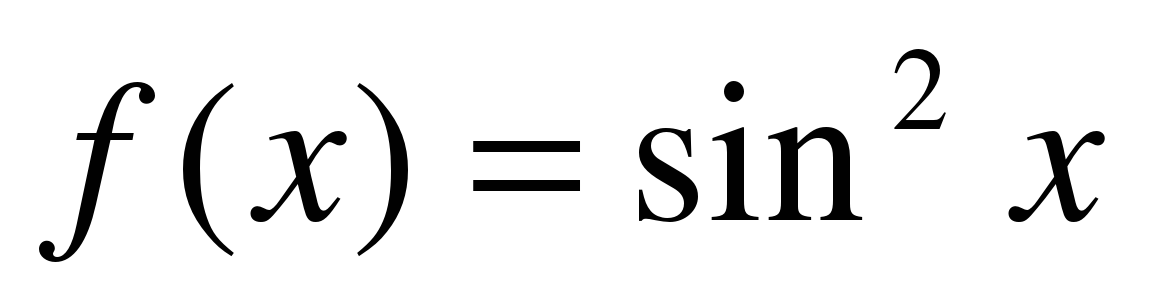
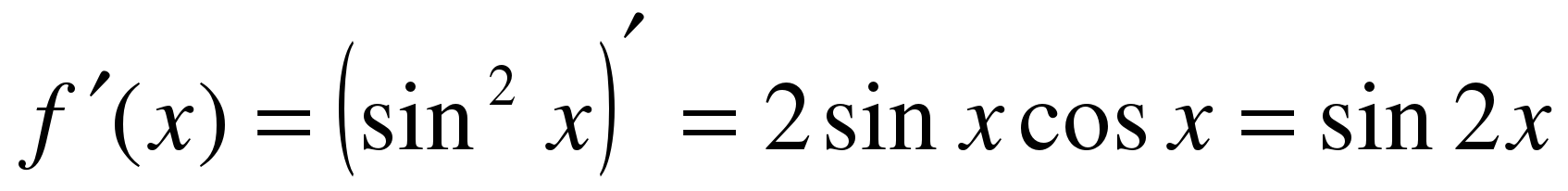
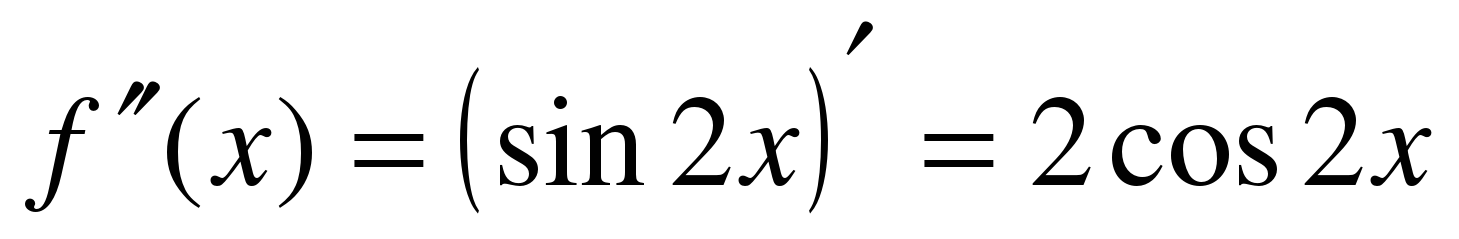
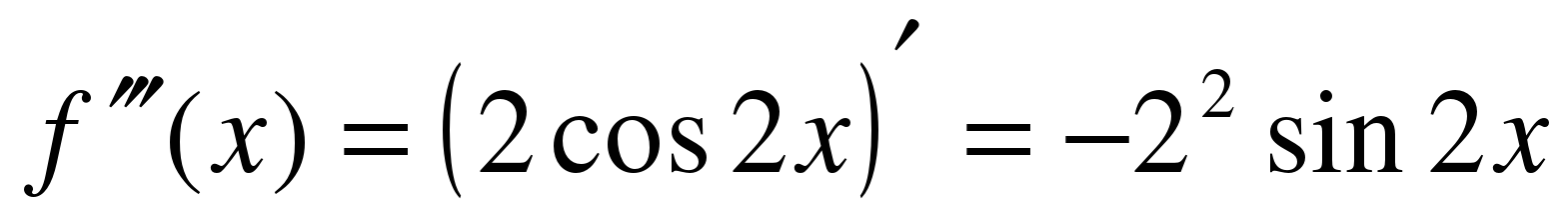
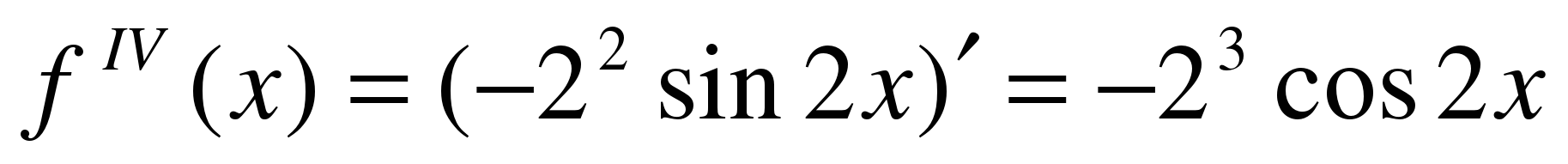
Находим значение функции и производных при :

……………

Подставляем полученные значения в формулу для разложения функции в ряд Маклорена:

2 способ:

Представим

Воспользуемся известным разложением в ряд Маклорена для функции :

Тогда разложение функции будет:

Имеем для заданной функции:

Нетрудно видеть, что результат, полученный обоими способами, совпадает.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.

9.1. Найти область сходимости степенного ряда:

а) б)

в) г)

д) е) ж)

з)

9.2. Разложить функцию в ряд Маклорена:

а) б) в) г) д)

е) ж) з)

4