Теорема Пифагора (8 класс)

Пифагор и его теорема

Выполнил ученик 8Б класса Кургузиков Дмитрий ,

Учитель Кашперова Г.П.

Пифагор Самосский. (Pythagoras of Samos)

Биографические сведения : Пифагор

Родился около 570, умер около 500 до н.э. Древнегреческий философ и математик, основатель пифагорейской школы; преобразовал математику из собрания формул и рецептов в абстрактную дедуктивную науку, ему приписывают изучение свойств целых чисел и пропорций, доказательство теоремы о соотношении сторон прямоугольного треугольника. Письменных документов о Пифагоре не осталось. Известно, что Пифагор покинул свой родной остров Самос в Эгейском море у берегов Малой Азии в знак протеста против тирании правителя уже в зрелом возрасте (около 40 лет) и появился в греческом городе Кретоне на юге Италии. Он много путешествовал по странам Востока : был в Египте, в Вавилоне, где познакомился с восточной математикой. Математика стала частью его учения. Пифагор впервые разделил числа на четные и нечетные, простые и составные, ввел понятие фигурного числа

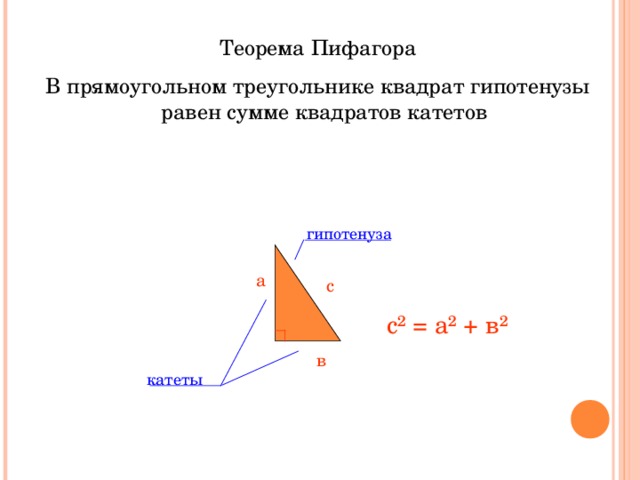
Теорема Пифагора

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

гипотенуза

а

с

с ² = а ² + в ²

в

катеты

a

b

Дано:

Прямоугольный треугольник с катетами a, b гипотенузой c

Доказать:

a 2 +b 2 =c 2

Доказательство:

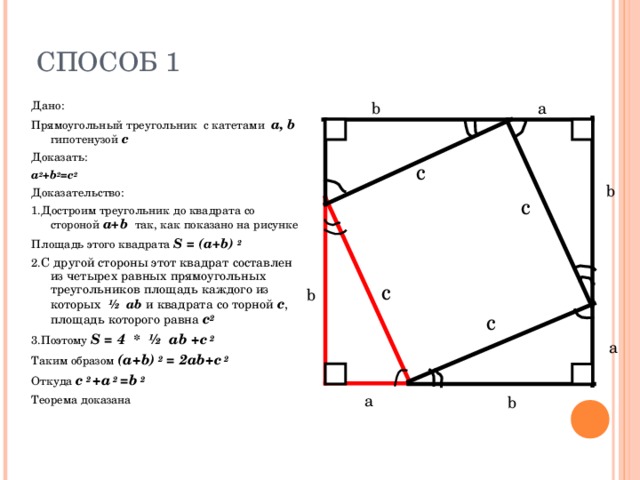
1.Достроим треугольник до квадрата со стороной a+b так, как показано на рисунке

Площадь этого квадрата S = (a+b) 2

2. С другой стороны этот квадрат составлен из четырех равных прямоугольных треугольников площадь каждого из которых ½ ab и квадрата со торной с , площадь которого равна c 2

3. Поэтому S = 4 * ½ ab +c 2

Таким образом (a+b) 2 = 2ab+c 2

Откуда c 2 + a 2 =b 2

Теорема доказана

c

b

c

c

b

c

a

a

b

Дано

Прямоугольник с катетами a , b и гипотенузой с

Доказать:

a 2 +b 2 =c 2

Доказательство:

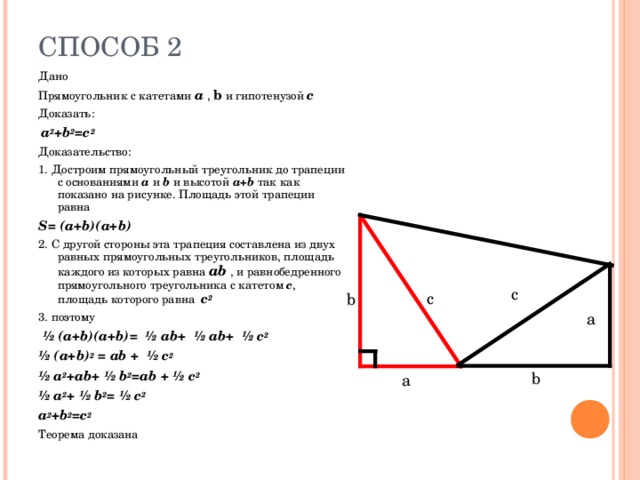
1. Достроим прямоугольный треугольник до трапеции с основаниями a и b и высотой a + b так как показано на рисунке. Площадь этой трапеции равна

S = ( a + b )( a + b )

2. С другой стороны эта трапеция составлена из двух равных прямоугольных треугольников, площадь каждого из которых равна ab , и равнобедренного прямоугольного треугольника с катетом с , площадь которого равна c 2

3. поэтому

½ (a+b)(a+b)= ½ ab+ ½ ab+ ½ c 2

½ (a+b) 2 = ab + ½ c 2

½ a 2 +ab+ ½ b 2 =ab + ½ c 2

½ a 2 + ½ b 2 = ½ c 2

a 2 +b 2 =c 2

Теорема доказана

c

c

b

a

b

a

КОНЕЦ