Просмотр содержимого документа
«Тест по теме: геометрическая прогрессия»
Геометрическая прогрессия Вариант - 1
1.Одна из последовательностей является геометрической прогрессией. Укажите эту последовательность. 1) 1; 3; 4; 6; . . . 2) 1; 3; 9; 27; . . . 3) 1; 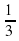 ;
;  ;
;  ; . . . 4) 5; 10; 25; 100; . . .
; . . . 4) 5; 10; 25; 100; . . .
2.Выписано несколько последовательных членов геометрической прогрессии: . . .; 2; х; 18; -54; . . . Найдите член прогрессии, обозначенный буквой X. 1) 6; 2) -6; 3) 9; 4) -9;
3. Указать формулу n - го члена геометрической прогрессии. 1) bn = b1 gn; 2) bn = b1 gn - 1; 3) bn = bn - 1 g; 4) bn + 1 = bn g;
4. Найти первый член геометрической прогрессии и её знаменатель, если b4 = 1 и b8 = 16. 1) b1 =8; g = 2. 2) b1 =  ; g = -2. 3) b1 =
; g = -2. 3) b1 =  ; g = 2. 4) b1 = 8; g =
; g = 2. 4) b1 = 8; g =  . 5. Дана конечная геометрическая прогрессия ( bn ). Найдите n, если b1 =
. 5. Дана конечная геометрическая прогрессия ( bn ). Найдите n, если b1 =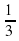 , g =
, g = 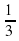 , bn =
, bn =  . 1) 4; 2) 5; 3) 6; 4) 7.
. 1) 4; 2) 5; 3) 6; 4) 7.
6. Геометрическая прогрессия задана условиями: b1 = 3, bn +1 = 3bn. Какое из данных чисел является членом этой прогрессии? 1) 6; 2) 12; 3) 24; 4) 27;
7. Составить формулу n - го члена геометрической прогрессии, если b1 = 2, g = 3. 1) bn= 2 · 3n; 2) bn = 3 · 2n - 1; 3) bn = 2 · 3n -1; 4) bn = 3 ·2n.
8. Найти число членов геометрической прогрессии, если b1 = -1; g = 4; Sn = -341; 1) 4; 2) 5; 3) 6; 4)7.
9. Для геометрической прогрессии ( bn ) найти Sn , если: b1 = 5; g =2; n = 4. 1) 75; 2) 35; 3)150; 4) 315.
10. Чему равна сумма геометрической прогрессии 2; -  ;
;  . . . 1) -
. . . 1) -  ; 2) 2
; 2) 2 ; 3) 2; 4)
; 3) 2; 4)  .
.
Геометрическая прогрессия Вариант - 2
1.Одна из последовательностей является геометрической прогрессией. Укажите эту последовательность. 1) 2; 3; 4; 5; . . . 2) 1; 7; 21; 28; . . . 3) 5;  ;
; 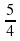 ;
;  ; . . . 4) 5; 10; 25; 100; . . .
; . . . 4) 5; 10; 25; 100; . . .
2.Выписано несколько последовательных членов геометрической прогрессии: . . .;  ; х; 6; 24; . . . Найдите член прогрессии, обозначенный буквой X. 1) 1,5; 2) -1,5; 3) 3; 4) -3;
; х; 6; 24; . . . Найдите член прогрессии, обозначенный буквой X. 1) 1,5; 2) -1,5; 3) 3; 4) -3;
3. Указать формулу n - го члена геометрической прогрессии. 1) Сn = C1 gn; 2) Сn = C1 gn - 1; 3) Сn = C n - 1 g; 4) Сn + 1 = Cn g;
4. Найти первый член геометрической прогрессии и её знаменатель, если b2 = 8 и b3 = -16. 1) b1 = 4; g = 2. 2) b1 =  ; g = -2. 3) b1 =
; g = -2. 3) b1 =  ; g = 2. 4) b1 = -4; g = -2
; g = 2. 4) b1 = -4; g = -2 . 5. Дана конечная геометрическая прогрессия ( bn ). Найдите n, если b1 =
. 5. Дана конечная геометрическая прогрессия ( bn ). Найдите n, если b1 = , g =
, g =  , bn =
, bn = 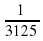 . 1) 4; 2) 5; 3) 6; 4) 7.
. 1) 4; 2) 5; 3) 6; 4) 7.
6. Геометрическая прогрессия задана условиями: b1 = 3, bn +1 = 2bn. Какое из данных чисел является членом этой прогрессии? 1) 9; 2) 12; 3) 32; 4) 27;
7. Составить формулу n - го члена геометрической прогрессии, если b1 = 3, g = 2. 1) bn= 2 · 3n; 2) bn = 3 · 2n - 1; 3) bn = 2 · 3n -1; 4) bn = 3 ·2n.
8. Найти число членов геометрической прогрессии, если b1 = 5; g = 2; Sn = 155 1) 4; 2) 5; 3) 6; 4)3.
9. Для геометрической прогрессии ( bn ) найти Sn , если: b1 = 6; g =2; n = 4. 1) 21; 2) 42; 3) 180; 4) 90.
10. Чему равна сумма геометрической прогрессии 3; -  ;
;  . . . 1) -
. . . 1) -  ; 2)
; 2)  ; 3) 4; 4) 2,4.
; 3) 4; 4) 2,4.





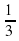 ;
;  ;
;  ; . . . 4) 5; 10; 25; 100; . . .
; . . . 4) 5; 10; 25; 100; . . . ; g = -2. 3) b1 =
; g = -2. 3) b1 =  . 5. Дана конечная геометрическая прогрессия ( bn ). Найдите n, если b1 =
. 5. Дана конечная геометрическая прогрессия ( bn ). Найдите n, если b1 = . 1) 4; 2) 5; 3) 6; 4) 7.
. 1) 4; 2) 5; 3) 6; 4) 7. ;
;  . . . 1) -
. . . 1) -  .
. ;
; 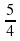 ;
;  ; . . . 4) 5; 10; 25; 100; . . .
; . . . 4) 5; 10; 25; 100; . . . ; х; 6; 24; . . . Найдите член прогрессии, обозначенный буквой X. 1) 1,5; 2) -1,5; 3) 3; 4) -3;
; х; 6; 24; . . . Найдите член прогрессии, обозначенный буквой X. 1) 1,5; 2) -1,5; 3) 3; 4) -3; . 5. Дана конечная геометрическая прогрессия ( bn ). Найдите n, если b1 =
. 5. Дана конечная геометрическая прогрессия ( bn ). Найдите n, если b1 = , g =
, g = 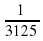 . 1) 4; 2) 5; 3) 6; 4) 7.
. 1) 4; 2) 5; 3) 6; 4) 7. ;
; 









