
Тренажер.
«Чтение» графиков
Программа составлена
по КИМ ЕГЭ.

Скоро ЕГЭ!
Еще есть время подготовиться!
![ПОДУМАЙ! Функция задана графиком. Укажите область определения этой функции. 7 6 5 4 3 2 1 ВЕРНО! [-2; 4] 1 ПОДУМАЙ! [-5; 5) 2 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 Это множество значений! 3 [-5; 5] 4 (-2; 4]](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img2.jpg)
ПОДУМАЙ!
Функция задана графиком.
Укажите область определения
этой функции.
7
6
5
4
3
2
1
ВЕРНО!
[-2; 4]
1
ПОДУМАЙ!
[-5; 5)
2
-7 -6 -5 -4 -3 -2 -1
1 2 3 4 5 6 7
-1
-2
-3
-4
-5
-6
-7
Это множество значений!
3
[-5; 5]
4
(-2; 4]
![ПОДУМАЙ! Функция задана графиком. Укажите множество значений этой функции. 7 6 5 4 3 2 1 ПОДУМАЙ! [-5; 7] 1 ВЕРНО! [-3; 5] 2 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 Это область определения! 3 (-5; 7) 4 (-3; 5)](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img3.jpg)
ПОДУМАЙ!
Функция задана графиком.
Укажите множество значений
этой функции.
7
6
5
4
3
2
1
ПОДУМАЙ!
[-5; 7]
1
ВЕРНО!
[-3; 5]
2
-7 -6 -5 -4 -3 -2 -1
1 2 3 4 5 6 7
-1
-2
-3
-4
-5
-6
-7
Это область определения!
3
(-5; 7)
4
(-3; 5)
![Функция задана графиком. Укажите область значений этой функции. ПОДУМАЙ! 7 6 5 4 3 2 1 Подумай! 1 [1; 6] ПОДУМАЙ! 2 [-6; 5) -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 3 ВЕРНО! [-2; 6] 4 (-2; 6]](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img4.jpg)
Функция задана графиком.
Укажите область значений
этой функции.
ПОДУМАЙ!
7
6
5
4
3
2
1
Подумай!
1
[1; 6]
ПОДУМАЙ!
2
[-6; 5)
-7 -6 -5 -4 -3 -2 -1
1 2 3 4 5 6 7
-1
-2
-3
-4
-5
-6
-7
3
ВЕРНО!
[-2; 6]
4
(-2; 6]
![Функция задана графиком. Укажите область определения этой функции. ПОДУМАЙ! 7 6 5 4 3 2 1 ВЕРНО! 1 [-3; 5] ПОДУМАЙ! 2 (-2; 5] -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 3 [-2; 5] Подумай ! [-3; 5) 4](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img5.jpg)
Функция задана графиком.
Укажите область определения
этой функции.
ПОДУМАЙ!
7
6
5
4
3
2
1
ВЕРНО!
1
[-3; 5]
ПОДУМАЙ!
2
(-2; 5]
-7 -6 -5 -4 -3 -2 -1
1 2 3 4 5 6 7
-1
-2
-3
-4
-5
-6
-7
3
[-2; 5]
Подумай !
[-3; 5)
4
![Функция задана графиком на [-4;0) (0;3]. Укажите множество значений этой функции. ПОДУМАЙ! 7 6 5 4 3 2 1 ВЕРНО! 1 [1; 3] ПОДУМАЙ! 2 [0; + ) -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 3 [1; + ] ПОДУМАЙ! 4 (-2; 4]](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img6.jpg)
Функция задана графиком на [-4;0) (0;3].
Укажите множество значений
этой функции.
ПОДУМАЙ!
7
6
5
4
3
2
1
ВЕРНО!
1
[1; 3]
ПОДУМАЙ!
2
[0; + )
-7 -6 -5 -4 -3 -2 -1
1 2 3 4 5 6 7
-1
-2
-3
-4
-5
-6
-7
3
[1; + ]
ПОДУМАЙ!
4
(-2; 4]

Функция задана графиком.
Укажите наибольшее значение функции
ПОДУМАЙ!
7
6
5
4
3
2
1
5
ВЕРНО!
1
2
4
ПОДУМАЙ!
-7 -6 -5 -4 -3 -2 -1
1 2 3 4 5 6 7
-1
-2
-3
-4
-5
-6
-7
3
3
ПОДУМАЙ!
4
-4
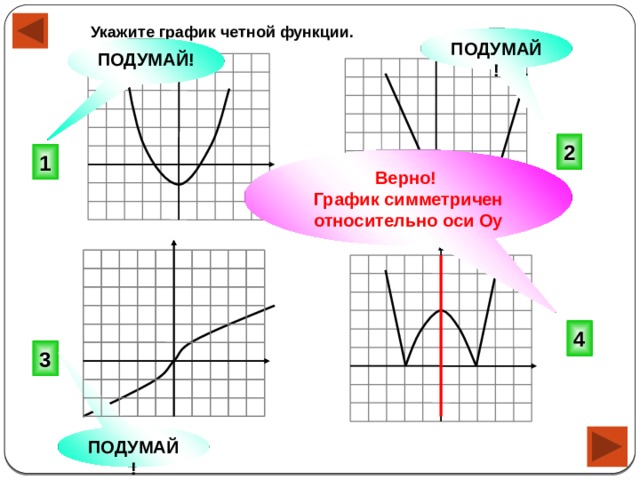
Укажите график четной функции.
ПОДУМАЙ!
ПОДУМАЙ!
2
1
Верно!
График симметричен относительно оси Оу
4
3
ПОДУМАЙ!
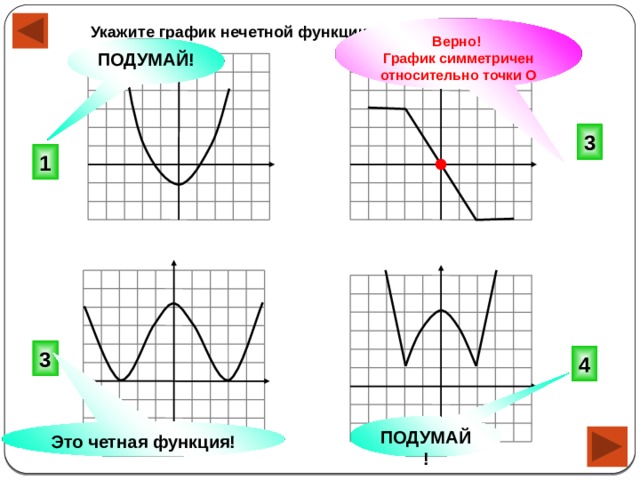
Верно!
Укажите график нечетной функции.
График симметричен относительно точки О
ПОДУМАЙ!
3
1
3
4
ПОДУМАЙ!
Это четная функция!
 o. Из прямоугольного треугольника находим tg α = 4 : 4 =1 1 " width="640"
o. Из прямоугольного треугольника находим tg α = 4 : 4 =1 1 " width="640"
На рисунке изображен график функции у =f(x) и касательная
к нему в точке с абсциссой х 0 .
Найдите значение производной в точке х 0 .
Подумай!
-5
Подумай!
х 0
-1
Подумай!
5
Верно!
Геометрический смысл производной: k = tg α
Угол наклона касательной с осью Ох острый, значит k o.
Из прямоугольного треугольника
находим tg α = 4 : 4 =1
1

На рисунке изображен график функции у =f(x) и касательная
к нему в точке с абсциссой х 0 .
Найдите значение производной в точке х 0 .
Верно!
0
Подумай!
1
Подумай!
х 0
Подумай!
-1
Не существует
Геометрический смысл производной: k = tg α
Угол наклона касательной с осью Ох равен 0 (касательная параллельна оси Ох),
значит tg 0 = 0

На рисунке изображен график функции у =f(x)
Найдите значение производной в точке х 0 .
Верно!
Не существует
Подумай!
1
Подумай!
х 0
-1
Подумай!
2
![На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите точку, в которой производная равна 0. Не верно! 1 1 Верно! 1 2 3 4 5 х -4 -3 -2 -1 2 -1 Не верно! 1 3 Не верно 4 -3](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img13.jpg)
На рисунке изображен график функции у =f(x),
заданной на промежутке [-5;5].
Укажите точку, в которой производная равна 0.
Не верно!
1
1
Верно!
1 2 3 4 5 х
-4 -3 -2 -1
2
-1
Не верно!
1
3
Не верно
4
-3

На рисунке изображен график функции у =f(x) и касательная
к нему в точке с абсциссой х 0 .
Найдите значение производной в точке х 0 .
Подумай!
0,5
Подумай!
х 0
-0,5
Верно!
-2
Геометрический смысл производной: k = tg α
Угол наклона касательной с осью Ох тупой, значит k
Из прямоугольного треугольника
находим tg α = 6 : 3 =2. Значит, k= -2
Подумай!
2
 o. В этой точке производная равна нулю! х 1 х 1 х 2 х 3 х 4 х 2 х 3 Верно! Угол наклона касательной с осью Ох тупой, значит k х 4 " width="640"
o. В этой точке производная равна нулю! х 1 х 1 х 2 х 3 х 4 х 2 х 3 Верно! Угол наклона касательной с осью Ох тупой, значит k х 4 " width="640"
На рисунке изображен график функции у =f(x).
Укажите в какой точке значение производной отрицатально.
В этой точке производная не существует
Угол наклона касательной с осью Ох острый, значит k o.
В этой точке производная равна нулю!
х 1
х 1 х 2 х 3 х 4
х 2
х 3
Верно!
Угол наклона касательной с осью Ох тупой, значит k
х 4
![На рисунке изображен график функции у =f(x), заданной на промежутке [-4;5]. Укажите промежуток, которому принадлежит один нуль функции. Подумай! Подумай! 1 [-3; 1) 1 2 3 4 5 х Верно! -4 -3 -2 -1 2 [-3; 1] Подумай! 3 (-3;-1] Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох. 4 (-3; 5)](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img16.jpg)
На рисунке изображен график функции у =f(x),
заданной на промежутке [-4;5].
Укажите промежуток, которому принадлежит один нуль функции.
Подумай!
Подумай!
1
[-3; 1)
1 2 3 4 5 х
Верно!
-4 -3 -2 -1
2
[-3; 1]
Подумай!
3
(-3;-1]
Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох.
4
(-3; 5)
![На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите промежуток, которому принадлежат два нуля функции. Верно! Подумай! 1 (1; 4] 1 2 3 4 5 х Подумай! -4 -3 -2 -1 2 [-3; 3) Подумай! 3 [-3;2] Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох. [-3; 5) 4](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img17.jpg)
На рисунке изображен график функции у =f(x),
заданной на промежутке [-5;5].
Укажите промежуток, которому принадлежат два нуля функции.
Верно!
Подумай!
1
(1; 4]
1 2 3 4 5 х
Подумай!
-4 -3 -2 -1
2
[-3; 3)
Подумай!
3
[-3;2]
Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох.
[-3; 5)
4
![На рисунке изображен график функции у =f(x), заданной на промежутке [-4;5]. Укажите промежуток, которому принадлежат все нули функции. Верно! Подумай! [-3;4] 1 1 2 3 4 5 х Подумай! -4 -3 -2 -1 2 (-3; 5) Подумай! 3 (-3;4] Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох. (1; 4] 4](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img18.jpg)
На рисунке изображен график функции у =f(x),
заданной на промежутке [-4;5].
Укажите промежуток, которому принадлежат все нули функции.
Верно!
Подумай!
[-3;4]
1
1 2 3 4 5 х
Подумай!
-4 -3 -2 -1
2
(-3; 5)
Подумай!
3
(-3;4]
Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох.
(1; 4]
4
![На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите промежуток, которому принадлежат один экстремум функции функции. Верно! Подумай! 1 [ -2; 2] 1 2 3 4 5 х Подумай! -4 -3 -2 -1 2 [-3; 3] Подумай! 3 [-3;2] [-3; 5) 4 Экстремумы функции – значения x max и x min ..](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img19.jpg)
На рисунке изображен график функции у =f(x),
заданной на промежутке [-5;5].
Укажите промежуток, которому принадлежат один экстремум функции функции.
Верно!
Подумай!
1
[ -2; 2]
1 2 3 4 5 х
Подумай!
-4 -3 -2 -1
2
[-3; 3]
Подумай!
3
[-3;2]
[-3; 5)
4
Экстремумы функции – значения x max и x min ..
![На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите расстояние между точками экстремума. Подумай! Подумай! 1 2 1 2 3 4 5 х Верно! -4 -3 -2 -1 2 3 Подумай! 3 4 Экстремумы функции – значения x max и x min .. 10 4](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img20.jpg)
На рисунке изображен график функции у =f(x),
заданной на промежутке [-5;5].
Укажите расстояние между точками экстремума.
Подумай!
Подумай!
1
2
1 2 3 4 5 х
Верно!
-4 -3 -2 -1
2
3
Подумай!
3
4
Экстремумы функции – значения x max и x min ..
10
4
![На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите точку максимума . Точка перегиба! 1 Подумай! -1 1 2 3 4 5 х -4 -3 -2 -1 2 4 Верно! 3 Точка минимума! 1 4 -3](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img21.jpg)
На рисунке изображен график функции у =f(x),
заданной на промежутке [-5;5].
Укажите точку максимума .
Точка перегиба!
1
Подумай!
-1
1 2 3 4 5 х
-4 -3 -2 -1
2
4
Верно!
3
Точка минимума!
1
4
-3
![В. На рисунке изображен график производной функции у =f / (x), заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на монотонность и укажите число промежутков убывания . Не верно! y = f / (x) + + - - - 1 Верно! 1 1 2 3 4 5 х -4 -3 -2 -1 3 2 Не верно! 2 3 Не верно! f / (x) - + - + - 4 4 f(x) -4 -2 0 4](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img22.jpg)
В. На рисунке изображен график производной функции у =f / (x),
заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на
монотонность и укажите число промежутков убывания .
Не верно!
y = f / (x)
+ +
- - -
1
Верно!
1
1 2 3 4 5 х
-4 -3 -2 -1
3
2
Не верно!
2
3
Не верно!
f / (x) - + - + -
4
4
f(x) -4 -2 0 4
![В. На рисунке изображен график производной функции у =f / (x), заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на монотонность и укажите число точек минимума . Не верно! y = f / (x) + + + - - - Верно! 1 1 1 2 3 4 5 х -4 -3 -2 -1 2 3 Не верно! 2 3 Не верно! f / (x) - + - + - + 4 4 f(x) -4 -2 0 3 4](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img23.jpg)
В. На рисунке изображен график производной функции у =f / (x),
заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на
монотонность и укажите число точек минимума .
Не верно!
y = f / (x)
+ + +
- - -
Верно!
1
1
1 2 3 4 5 х
-4 -3 -2 -1
2
3
Не верно!
2
3
Не верно!
f / (x) - + - + - +
4
4
f(x) -4 -2 0 3 4
![В. На рисунке изображен график производной функции у =f / (x), заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на монотонность и укажите наибольшую точку максимума . Из двух точек максимума наибольшая х max = 3 Не верно! y = f / (x) + + + - - - Верно! 1 5 1 2 3 4 5 х -4 -3 -2 -1 2 3 Не верно! 2 3 Не верно! f / (x) - + - + - + 4 4 f(x) -4 -2 0 3 4](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img24.jpg)
В. На рисунке изображен график производной функции у =f / (x),
заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на
монотонность и укажите наибольшую точку максимума .
Из двух точек максимума наибольшая х max = 3
Не верно!
y = f / (x)
+ + +
- - -
Верно!
1
5
1 2 3 4 5 х
-4 -3 -2 -1
2
3
Не верно!
2
3
Не верно!
f / (x) - + - + - +
4
4
f(x) -4 -2 0 3 4
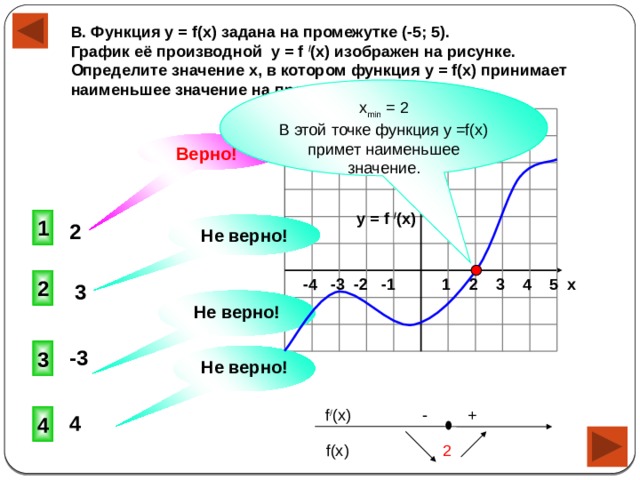
В. Функция y = f(x) задана на промежутке (-5; 5).
График её производной y = f / (x) изображен на рисунке.
Определите значение х, в котором функция у = f(x) принимает
наименьшее значение на промежутке ( -5; 5).
х min = 2
В этой точке функция у =f(x) примет наименьшее значение.
Верно!
y = f / (x)
1
2
Не верно!
2
-4 -3 -2 -1
1 2 3 4 5 х
3
Не верно!
-3
3
Не верно!
f / (x) - +
4
4
f(x) 2

1 . На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .
В 8
0
,
7
5

3. На рисунке изображен график функции , определенной на интервале . Найдите сумму точек экстремума функции.
-2+1+3+4+5+8+10=…
-2
5
4
3
.
1
10
8
В 8
2
9

5. На рисунке изображен график функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой .
.
В8
6

8. На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых производная функции отрицательна .
В8
8
 0; 2) функция y=f(x) убывает на промежутках, где производная y=f ‘(x)3) функция y=f(x) имеет критические точки, где производная f ‘(x)=0 или не существует (но это верно только для внутренних точек области определения, то есть точки на концах области определения не рассматриваем); 4) функция y=f(x) имеет точки экстремума там, где производная y =f ‘(x) меняет свой знак. В частности, функция y=f(x) имеет точки максимума там, где производная меняет знак с плюса на минус; функция y=f(x) имеет точки минимума там, где производная меняет знак с минуса на плюс. " width="640"
0; 2) функция y=f(x) убывает на промежутках, где производная y=f ‘(x)3) функция y=f(x) имеет критические точки, где производная f ‘(x)=0 или не существует (но это верно только для внутренних точек области определения, то есть точки на концах области определения не рассматриваем); 4) функция y=f(x) имеет точки экстремума там, где производная y =f ‘(x) меняет свой знак. В частности, функция y=f(x) имеет точки максимума там, где производная меняет знак с плюса на минус; функция y=f(x) имеет точки минимума там, где производная меняет знак с минуса на плюс. " width="640"
Задания, в которых на рисунке изображен график производной функции y=f‘(x), и нужно определить точки экстремума и промежутки монотонности функции y=f(x), решаются очень просто.
Достаточно помнить, что
1) функция y=f(x) возрастает на промежутках, где производная y=f‘(x)0;
2) функция y=f(x) убывает на промежутках, где производная y=f ‘(x)
3) функция y=f(x) имеет критические точки, где производная f ‘(x)=0 или не существует (но это верно только для внутренних точек области определения, то есть точки на концах области определения не рассматриваем);
4) функция y=f(x) имеет точки экстремума там, где производная y =f ‘(x) меняет свой знак.
В частности, функция y=f(x) имеет точки максимума там, где производная меняет знак с плюса на минус;
функция y=f(x) имеет точки минимума там, где производная меняет знак с минуса на плюс.
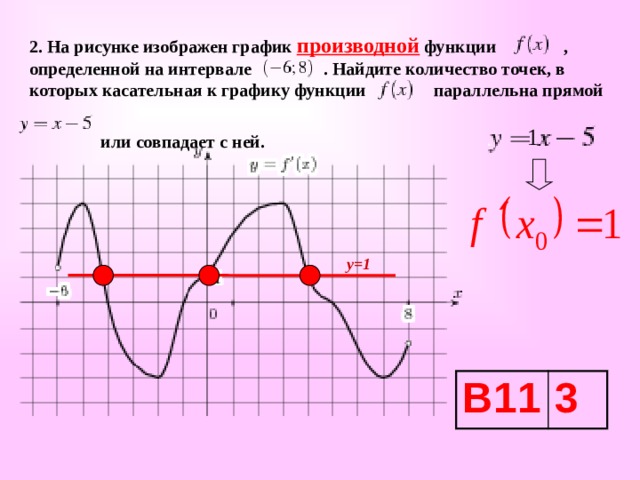
2. На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой
или совпадает с ней.
у=1
В11
3

4. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки убывания функции . В ответе укажите длину наибольшего из них.
В8
6

6. На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.
-3
В8
4

7. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.
-1
1
2
3
4
0
-1+0+1+2+3+4=…
В8
9
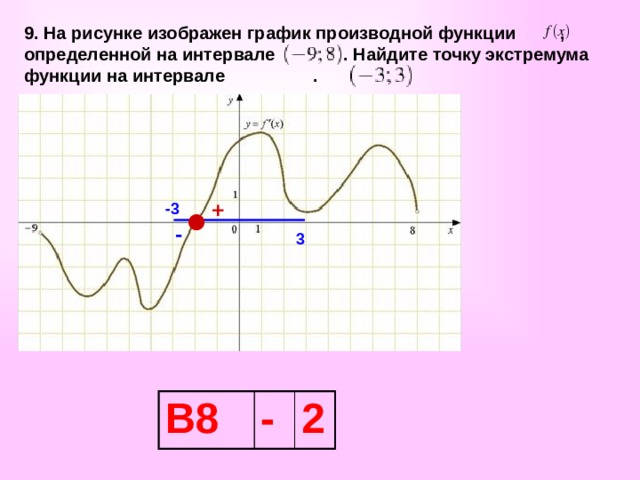
9. На рисунке изображен график производной функции , определенной на интервале . Найдите точку экстремума функции на интервале .
-3
+
-
3
В8
-
2

10. На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка функция принимает наименьшее значение.
+
2
-
-3
3
В8
2

Скоро ЕГЭ!
Еще есть время подготовиться!







![ПОДУМАЙ! Функция задана графиком. Укажите область определения этой функции. 7 6 5 4 3 2 1 ВЕРНО! [-2; 4] 1 ПОДУМАЙ! [-5; 5) 2 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 Это множество значений! 3 [-5; 5] 4 (-2; 4]](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img2.jpg)
![ПОДУМАЙ! Функция задана графиком. Укажите множество значений этой функции. 7 6 5 4 3 2 1 ПОДУМАЙ! [-5; 7] 1 ВЕРНО! [-3; 5] 2 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 Это область определения! 3 (-5; 7) 4 (-3; 5)](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img3.jpg)
![Функция задана графиком. Укажите область значений этой функции. ПОДУМАЙ! 7 6 5 4 3 2 1 Подумай! 1 [1; 6] ПОДУМАЙ! 2 [-6; 5) -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 3 ВЕРНО! [-2; 6] 4 (-2; 6]](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img4.jpg)
![Функция задана графиком. Укажите область определения этой функции. ПОДУМАЙ! 7 6 5 4 3 2 1 ВЕРНО! 1 [-3; 5] ПОДУМАЙ! 2 (-2; 5] -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 3 [-2; 5] Подумай ! [-3; 5) 4](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img5.jpg)
![Функция задана графиком на [-4;0) (0;3]. Укажите множество значений этой функции. ПОДУМАЙ! 7 6 5 4 3 2 1 ВЕРНО! 1 [1; 3] ПОДУМАЙ! 2 [0; + ) -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 3 [1; + ] ПОДУМАЙ! 4 (-2; 4]](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img6.jpg)



 o. Из прямоугольного треугольника находим tg α = 4 : 4 =1 1 " width="640"
o. Из прямоугольного треугольника находим tg α = 4 : 4 =1 1 " width="640"


![На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите точку, в которой производная равна 0. Не верно! 1 1 Верно! 1 2 3 4 5 х -4 -3 -2 -1 2 -1 Не верно! 1 3 Не верно 4 -3](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img13.jpg)

 o. В этой точке производная равна нулю! х 1 х 1 х 2 х 3 х 4 х 2 х 3 Верно! Угол наклона касательной с осью Ох тупой, значит k х 4 " width="640"
o. В этой точке производная равна нулю! х 1 х 1 х 2 х 3 х 4 х 2 х 3 Верно! Угол наклона касательной с осью Ох тупой, значит k х 4 " width="640"
![На рисунке изображен график функции у =f(x), заданной на промежутке [-4;5]. Укажите промежуток, которому принадлежит один нуль функции. Подумай! Подумай! 1 [-3; 1) 1 2 3 4 5 х Верно! -4 -3 -2 -1 2 [-3; 1] Подумай! 3 (-3;-1] Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох. 4 (-3; 5)](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img16.jpg)
![На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите промежуток, которому принадлежат два нуля функции. Верно! Подумай! 1 (1; 4] 1 2 3 4 5 х Подумай! -4 -3 -2 -1 2 [-3; 3) Подумай! 3 [-3;2] Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох. [-3; 5) 4](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img17.jpg)
![На рисунке изображен график функции у =f(x), заданной на промежутке [-4;5]. Укажите промежуток, которому принадлежат все нули функции. Верно! Подумай! [-3;4] 1 1 2 3 4 5 х Подумай! -4 -3 -2 -1 2 (-3; 5) Подумай! 3 (-3;4] Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох. (1; 4] 4](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img18.jpg)
![На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите промежуток, которому принадлежат один экстремум функции функции. Верно! Подумай! 1 [ -2; 2] 1 2 3 4 5 х Подумай! -4 -3 -2 -1 2 [-3; 3] Подумай! 3 [-3;2] [-3; 5) 4 Экстремумы функции – значения x max и x min ..](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img19.jpg)
![На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите расстояние между точками экстремума. Подумай! Подумай! 1 2 1 2 3 4 5 х Верно! -4 -3 -2 -1 2 3 Подумай! 3 4 Экстремумы функции – значения x max и x min .. 10 4](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img20.jpg)
![На рисунке изображен график функции у =f(x), заданной на промежутке [-5;5]. Укажите точку максимума . Точка перегиба! 1 Подумай! -1 1 2 3 4 5 х -4 -3 -2 -1 2 4 Верно! 3 Точка минимума! 1 4 -3](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img21.jpg)
![В. На рисунке изображен график производной функции у =f / (x), заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на монотонность и укажите число промежутков убывания . Не верно! y = f / (x) + + - - - 1 Верно! 1 1 2 3 4 5 х -4 -3 -2 -1 3 2 Не верно! 2 3 Не верно! f / (x) - + - + - 4 4 f(x) -4 -2 0 4](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img22.jpg)
![В. На рисунке изображен график производной функции у =f / (x), заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на монотонность и укажите число точек минимума . Не верно! y = f / (x) + + + - - - Верно! 1 1 1 2 3 4 5 х -4 -3 -2 -1 2 3 Не верно! 2 3 Не верно! f / (x) - + - + - + 4 4 f(x) -4 -2 0 3 4](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img23.jpg)
![В. На рисунке изображен график производной функции у =f / (x), заданной на промежутке [-5;5]. Исследуйте функцию у =f (x) на монотонность и укажите наибольшую точку максимума . Из двух точек максимума наибольшая х max = 3 Не верно! y = f / (x) + + + - - - Верно! 1 5 1 2 3 4 5 х -4 -3 -2 -1 2 3 Не верно! 2 3 Не верно! f / (x) - + - + - + 4 4 f(x) -4 -2 0 3 4](https://fsd.multiurok.ru/html/2020/08/19/s_5f3d095cebb36/img24.jpg)





 0; 2) функция y=f(x) убывает на промежутках, где производная y=f ‘(x)3) функция y=f(x) имеет критические точки, где производная f ‘(x)=0 или не существует (но это верно только для внутренних точек области определения, то есть точки на концах области определения не рассматриваем); 4) функция y=f(x) имеет точки экстремума там, где производная y =f ‘(x) меняет свой знак. В частности, функция y=f(x) имеет точки максимума там, где производная меняет знак с плюса на минус; функция y=f(x) имеет точки минимума там, где производная меняет знак с минуса на плюс. " width="640"
0; 2) функция y=f(x) убывает на промежутках, где производная y=f ‘(x)3) функция y=f(x) имеет критические точки, где производная f ‘(x)=0 или не существует (но это верно только для внутренних точек области определения, то есть точки на концах области определения не рассматриваем); 4) функция y=f(x) имеет точки экстремума там, где производная y =f ‘(x) меняет свой знак. В частности, функция y=f(x) имеет точки максимума там, где производная меняет знак с плюса на минус; функция y=f(x) имеет точки минимума там, где производная меняет знак с минуса на плюс. " width="640"

















