Тренажер "Действия с положительными и отрицательными числами. Решение уравнений" предназначен для домашнего выполнения. Тренажер включает таблицу с примерами на сложение, вычитание, умножение и делений положительных и отрицательных чисел, уравнения и задачу, которая решается с помощью уравнения.
Просмотр содержимого документа
«Тренажер "Действия с положительными и отрицательными числами. Решение уравнений". 6 класс»
Фамилия Имя _______________________________________________________________ Вариант 1
Выполните действия:
| 1 | 1 + (5) = | 1 + (5) = | 1 (5) = | 1 (5) = | 12 (4) = |
| 2 | 17 + (5) = | 7 + 5 = | 7 (5) = | 9 (5) = | 90 (9) = |
| 3 | 100 + (12) = | 10 + 12 = | 10 (12) = | 10 (12) = | 24 (1,2) = |
| 4 | 1,2 + (8) = | 120 + 8 = | 102 8 = | 20 (8) = | 240 (8) = |
| 5 | 9,7 + (0,5) = | 9,7 + (5) = | 97 (0,5) = | 7 (0,5) = | 70 (0,5) = |
| 6 | 1,5 + (0,23) = | 15 + (0,23) = | 1,5 (2,3) = | 1,5 3 = | 1,5 3 = |
| 7 | 19 + (19) = | 19 + (19) = | 19 (19) = | 10 (10) = | 10 (10) = |
| 8 | 20,8 + (280) = | 20,8 + 280 = | 20,8 (280) = | 80 (80) = | 800 (80) = |
| 9 | 5 + (80) = | 5 + 80 = | 5 (80) = | 5 (80) = | 56 (2) = |
| 10 | 1000 + (1) = | 1000 + 1 = | 1000 (1) = | 1000 (1) = | 10 (100) = |
| 11 | 36 + (700) = | 36 + 700 = | 36 700 = | 0,3 70 = | 1,3 10 = |
| 12 | 0,5 + (0,5) = | 0,5 + 0,5 = | 0,5 (0,5) = | 0,1 (0,1) = | 0,1 (0,1) = |
| 13 | 1,02 + (5,4) = | 1,2 + (5,4) = | 1,2 5,4 = | 10 5,04 = | 60 1,2 = |
| 14 | 5,5 + (0,65) = | 5,5 + 0,65 = | 5,5 (0,55) = | 5 (0,25) = | 5 (0,05) = |
| 15 | 2,95 + (1,02) = | 2,5 + 1,02 = | 2,5 (1,2) = | 2,5 (0,4) = | 2,4 (0,4) = |
Упростите выражения:
| 1 | 6х3у(5) = | 8x (5) + 1,8 ∙ 5x 2x = |
| 2 | 0,5a (2,4b) = | 4m (2m 3) + (m 15) = |
| 3 | 2m + 3m 6m = | (7x + 6y) 5 3 (4y 15x) = |
| 4 | a 0,5a 0,3a + 2a = | 2х (х + 1) 2 (4 – х) = |
| 5 | 5k + 12p 8k 13p + 7k = | 0,4 (0,9 5х) + 2,5 (4х 1) 1,5 (2х 20) = |
Решите уравнения:
0,87х 0,9х + 1,3х = 15,24 х = ______________
20 (х 13) = 220 х = ______________
(3х 1,2) ∙ 7 = 10,5 х = ______________
5у + 27 = 4у + 21 у = ______________
7m 11 = 10m + 16 m = ______________
5,6 + 0,6х = 0,3х 1,3 х = ______________
 х +
х +  х – 1 = 1
х – 1 = 1 х = ______________
х = ______________
3 ∙ (4а 8) = 3а 6 а = ______________
Решите задачу с помощью уравнения:
На одной полке было в 7 раз больше книг, чем на другой. Когда с одной полки сняли 14 книг, а на другую положили 58 книг, то на полках стало книг поровну. Сколько книг было на каждой полке первоначально?
Решение:
1) Пусть х книг было на ________________________________, тогда ______ было на ________________________________. Зная, что после того как количество книг на первой полке уменьшилось на _____ книг, а на второй полке увеличилось на ______ книг, количество книг на полках стало одинаковое, составляем уравнение:
_______________________________________
_______________________________________
_______________________________________
_______________________________________
х = __________ ( _____ ) - _______________________________________________________
2) ____________________________________________________________________________
Ответ: ________________________________________________________________________
Фамилия Имя _______________________________________________________________ Вариант 2
Выполните действия:
| 1 | 1 + (5) = | 1 + (5) = | 1 (5) = | 1 (5) = | 12 (4) = |
| 2 | 7 + (5) = | 7 + 5 = | 7 (5) = | 9 (5) = | 90 (9) = |
| 3 | 10 + (12) = | 10 + 12 = | 10 (12) = | 10 (12) = | 24 (12) = |
| 4 | 12 + (8) = | 12 + 8 = | 12 8 = | 2 (8) = | 240 (8) = |
| 5 | 97 + (5) = | 97 + (5) = | 97 (5) = | 7 (5) = | 70 (5) = |
| 6 | 15 + (23) = | 15 + (23) = | 15 (23) = | 15 3 = | 15 3 = |
| 7 | 19 + (19) = | 19 + (19) = | 19 (19) = | 10 (10) = | 10 (10) = |
| 8 | 208 + (280) = | 208 + 280 = | 208 (280) = | 80 (80) = | 800 (80) = |
| 9 | 5 + (80) = | 5 + 80 = | 5 (80) = | 5 (80) = | 56 (2) = |
| 10 | 1000 + (1) = | 1000 + 1 = | 1000 (1) = | 1000 (1) = | 10 (100) = |
| 11 | 36 + (700) = | 36 + 700 = | 36 700 = | 3 70 = | 13 10 = |
| 12 | 0,5 + (0,5) = | 0,5 + 0,5 = | 0,5 (0,5) = | 0,1 (0,1) = | 0,1 (0,1) = |
| 13 | 1,2 + (5,4) = | 1,2 + (5,4) = | 1,2 5,4 = | 10 5,04 = | 60 1,2 = |
| 14 | 5,5 + (0,5) = | 5,5 + 0,5 = | 5,5 (0,5) = | 5 (0,5) = | 5 (0,5) = |
| 15 | 2,5 + (1,2) = | 2,5 + 1,2 = | 2,5 (1,2) = | 25 (0,4) = | 2,4 (0,4) = |
Упростите выражения:
| 1 | 6х3у(5) = | 8x (5) 2x = |
| 2 | 5a (24b) = | 4m (2m 3) + 15 = |
| 3 | 2m + 3m 6m = | 5 (7x + 6y) 3 (4y 15x) = |
| 4 | a 5a 3a + 2a = | 2х (х + 1) (4 – х) = |
| 5 | 5k + 12p 8k 13p + 7k = | 4 (9 5х) + 25 (4х 1) 15 (2х 2) = |
Решите уравнения:
87х 9х + 13х = 154 х = ______________
20 (х 13) = 220 х = ______________
(3х 1,2) ∙ 7 = 10,5 х = ______________
5у + 27 = 4у + 21 у = ______________
7m 11 = 10m + 16 m = ______________
56 + 6х = 3х 13 х = ______________
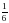 х +
х +  х – 1 =
х – 1 =  х = ______________
х = ______________
3 ∙ (4а 8) = 3а 6 а = ______________
Решите задачу с помощью уравнения:
На одной полке было в 7 раз больше книг, чем на другой. Когда с одной полки сняли 14 книг, а на другую положили 58 книг, то на полках стало книг поровну. Сколько книг было на каждой полке первоначально?
Решение:
1) Пусть х книг было на ________________________________, тогда ______ было на ________________________________. Зная, что после того как количество книг на первой полке уменьшилось на _____ книг, а на второй полке увеличилось на ______ книг, количество книг на полках стало одинаковое, составляем уравнение:
_______________________________________
_______________________________________
_______________________________________
_______________________________________
х = __________ ( _____ ) - _______________________________________________________
2) ____________________________________________________________________________
Ответ: ________________________________________________________________________





 х +
х +  х – 1 = 1
х – 1 = 1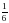 х +
х + 









