«Тригонометрические уравнения и некоторые методы их решения»
Предмет:
Алгебра и начала анализа
Класс: 10
Составила:
Учитель первой категории
Лобашева Людмила Михайловна
Урок по теме «Тригонометрические уравнения и методы их решения»
Тип урока: Урок применения знаний на практике. Форма урока: Деловая игра
Формы работы учащихся: Фронтальная, индивидуальная, групповая.
Оборудование: Компьютер, экран, слайды презентации, тесты, оформленная доска, оценочные списки,4 ноутбука за отдельным столом, столы расставлены по 2, для работы3х групп по 5 человек.
Цель урока: Довести до сознания и осмысления способы решения тригонометрических уравнений, сводимых к алгебраическим.
Задачи урока:
Обучающие:
Формирование представлений о видах тригонометрических уравнений и способах их решения, расширение круга знаний по тригонометрическим уравнениям;
Приобретение опыта применения знаний о квадратных уравнениях и уравнениях, решаемых разложением на множители к тригонометрическим уравнениям.
Развивающие:
Умение определять вид уравнения, устанавливать причинно-следственные связи, строить логические рассуждения и алгоритмы, делать выводы;
Умение применять алгоритм к решению уравнений и действовать согласно выстроенного плана;
Умение оценивать правильность выполнения учебной задачи, собственные возможности в поисках решения.
Воспитательные:
Воспитывать интерес к предмету и к данной теме, в частности, посредством игровых моментов и метапредметных связей;
Формирование коммуникативных учебных действий через общение и сотрудничество со сверстниками;
Формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к познанию.
Формируемые УУД:
Познавательные
Умение выделять типы уравнений и способы их решения;
Установление логических связей между имеющейся базой знаний о квадратных уравнениях и тригонометрическими уравнениями;
Применение знаний в измененных условиях;
Формирование мыслительных операций( классификация, синтез, аналогия, анализ);
Обоснование этапов решения, преобразование информации (использование для решения тригонометрических уравнений знаний о разложении на множители);
Умение строить алгоритмы.
Умение переводить информацию на математический. Символьный язык и наоборот.
Коммуникативные
Сотрудничество учащихся, умение слушать партнера, договариваться, распределять роли, взаимно контролировать друг друга;
Формирование речевых умений (комментируют решение друг другу, используя специальные термины), учатся формулировать вопросы и ответы.
Регулятивные
Умение находить ошибки (мысленное сравнение с эталоном);
Самопроверка и взаимоконтроль;
Оценка собственных результатов навыков решения уравнений;
Составление алгоритма и определение плана действий;
Формулирование цели урока;
Оценка партнера.
Личностные
Формирование этических норм общения и сотрудничества, необходимых как для всех вместе, так и для каждого в отдельности;
Личное участие в работе группы (в коллективе);
Самооценка;
Развитие мыслительных процессов, творчества.
Структура урока
| Этап урока | Деятельность учителя | Деятельность учеников | Формируемые и используемые УУД | время |
| Организационный | Ознакомление учеников и гостей с игровой ситуацией, требованиями и правилами игры. | Сообщение о готовности к уроку и принятия условий игры | Умение корректировать свои действия и эмоции, осознанно строить речевые высказывания. | 2мин. |
| Актуализация знаний | По заготовленному материалу на доске задает вопросы, комментирует и корректирует ответы | Отвечают на вопросы по материалам прошлых уроков. | Анализ, построение логической цепи рассуждений, доказательство (формирование мыслительных операций) | 5мин |
| Постановка цели урока | Подводит наводящими вопросами и предлагает сформулировать цель урока, мотивирует к дальнейшей деятельности | Формулируют цель урока | Целеполагание, подведение под понятия | 2мин |
| Закрепление знаний, постановка проблемы, первичная проверка знаний | Презентация уравнений. Ставит проблему, предлагает найти способы решения Проверяет ответы (слайд) | Отвечают на вопросы, предлагают пути решения, обговаривают приемы. Делают записи в тетрадях. | Элементы волевой саморегуляции, знаково-символические действия, обоснование этапов решения, преобразование информации, применение знаний в измененных условиях, формирование речевых умений с использованием математических терминов. Выбор наиболее эффективных способов решения в зависимости от условий. | 8мин |
| Закрепление знаний (Тренинг-контроль) | Демонстрация слайда с заданием, распределение ролей, пояснение условий работы. Наблюдение за работой учащихся. | Решают поставленные задачи. Работают в тетрадях. Комментируют решения друг другу. Оценивают работу товарищей. | Извлечение необходимой информации из только что прослушанного и проделанного, построение логической цепи рассуждений, оценка процесса и результатов деятельности, сотрудничество, умение слышать партнера, взаимный контроль, формирование речевых умений, определение алгоритма решения, соблюдение этических норм общения каждым и всеми, личное участие в работе группы, самооценка. | 13мин |
| Итог Подумай и ответь | Предлагает расклассифицировать решенные уравнения, сделать выводы и сформулировать какими методами их можно решать, предлагает творческое задание для каждой из групп по составлению алгоритма решения тех или иных уравнений. Мотивирует на следующий урок, ставя новую проблему. | Классифицируют уравнения, формулируют методы решения уравнений, составляют и обсуждают алгоритмы решений, представляют алгоритмы всему классу. | Формирование мыслительных операций (классификация, синтез, аналогия, анализ), умение последовательно и четко распределять свои действия в соответствии с заданным алгоритмом, установление логических связей , умение распределять роли, сотрудничать в группе, развитие творческих способностей и умение представлять себя публично. | 5мин |
| Рефлексия | Предлагает оценить самих себя, участие в уроке и сам урок, благодарит. | Оценивают деятельность на уроке и сам урок с помощью заготовленных заранее визиток. | Самооценка, оценка деятельности коллектива. | 2мин |
Ход урока
Огр. момент:
-Всем доброе утро! Господа, сегодня наш офис посетили гости – представители зарубежных фирм, с целью познакомиться с вами, с тем насколько вы конкурентоспособные, как компетентно вы можете вести дела и решать вопросы. Соответственно, от эффективности работы каждого из вас зависит слаженность работы всей компании в целом, а от этого зависит захотят ли зарубежные фирмы заключить с вами контракт о дальнейшем сотрудничестве, а насколько серьезно это для процветания фирмы и увеличения доходов сотрудников, думаю догадаться может каждый. Поэтому я желаю вам показать сегодня все свои лучшие стороны, умение слаженно вести работу, остроту ума, находчивость!
В начале я хотела бы дать небольшую справку о структуре нашей фирмы: в данном офисе работают три инициативные группы-компании, у каждой есть свой управляющий (представляются), человек, который может грамотно ответить на возникающие вопросы, принять правильное решение. И чтобы ни у кого не возникало сомнений в компетентности наших управляющих мы сейчас им предложим пройти тест-контроль, результат занести в таблицу, лежащую на столе. (3 человека работают на ноутбуках).
Актуализация знаний:
Ну а мы займемся небольшой подготовкой к нашему рабочему дню.
Наша фирма закончила работу над важным проектом «Решение простейших тригонометрических уравнений», где каждый приобрел некоторый ценный опыт и сейчас может смело им поделиться.
Внимание на экран:

Вычислить:
(слайд №1)
Задание 1. Заполните вторую колонку таблицы по цепочке. Выигрывает команда, которая выполнит задания верно и быстро.
Команда 1.
| Уравнение | Корень уравнения |
| cos x= a | x= |
| cos x=1 | x= |
| sin x=0 | x= |
| sin x=-1 | x= |
| tg x=a | x= |
Команда 2.
| Уравнение | Корень уравнения |
| cos x=0 | x= |
| cos x=-1 | x= |
| sin x=a | x= |
| sin x=1 | x= |
| tg x=a | x= |
Задание 2. Найдите и объясните ошибки при решение уравнений
а) sin(x+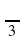 )=1,
)=1,
x+ 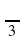 =
=  +2πn, n z,
+2πn, n z,
x=  +
+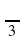 +2πn, n z.
+2πn, n z.
Ответ: x= +2πn, n z.
+2πn, n z.
б) (1-2cos x)(sin4x+1)=0
Приравняем к нулю каждый сомножитель:
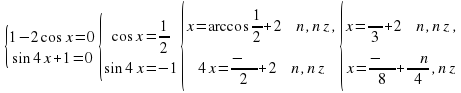
Ответ:  ;
; 
Задание 3. Установите соответствие между уравнением и его корнями.
| Уравнение | Корень уравнения |
|
1) 2sinxcosx=
|
А) πn, n z |
|
2) cos²x=1+sin²x
|
Б) π+2πk, k z |
|
3) 12cos4x=0
|
В) (-1) + + n, n, z z |
|
4) cos(π+x)=sin
|
Г) (-1) +πn, +πn, z z |
|
5) sin(π-x)-cos( +x)=√ 3 +x)=√ 3
|
Д)  + + n z n z |
Обобщение:
Назвать формулы для решения уравнений вида cos(x)=а; sinx=а;
tgx= а; ctgx=а.
Назвать основную тригонометрическую единицу.
Итак, господа , вы показали, что достаточно компетентны в данных вопросах и готовы к расширению сферы своей деятельности. Как вы думаете, чем предстоит вам заняться сегодня? (решением более сложных тригонометрических уравнений)
На экран проецируется тема урока «Тригонометрические уравнения и некоторые методы их решения» (слайд №8)
Мотивация:
Почему важно и зачем нужно знать и уметь решать тригонометрические уравнения? Эти уравнения применяются для расчета работы в физике, для определения углов в геометрии, для расчетов траекторий комет и метеоритов в астрономии. Этими уравнениями занимались такие знаменитые математики, как Франсуа Виет, Леонард Эйлер.

Тригонометрическими функциями описываются все гармонические колебания вокруг нас. А теперь, настраиваемся на серьезную работу, сделали глубокий вздох, слушаем и смотрим на экран.( фрагмент классической музыки Полонес Огинского) . Почему классическая музыка так приятна для слуха? Что вы наблюдали на экране? (правильно, это звуковые волны, которые распространяются по законам гармонических колебаний, что и описывают наши тригонометрические функции) Поэтому и название нашей фирмы – «Гармония».
Постановка проблемы: (внимание на экран)
Установите соответствие между уравнениями и его корнями
Закрепление (тренинг-контроль)
Теперь каждой компании дается проектное задание, состоящее из 6 уравнений. Решают их все, но каждый из вас по очереди должен объяснить решение своего уравнения партнеру, так чтобы это было логично, доступно, понятно (учимся работать с клиентами) Все мы понимаем, что как мы сами себя подадим, настолько с нами захотят сотрудничать! Управляющие следят за процессом, оценивают работу каждого индивидуально.
Подведение итогов (подумай и ответь) Прошу подумать и ответить мне на несколько вопросов:
Как бы вы проклассифицировали все те уравнения, с которыми пришлось столкнуться в ходе работы (на какие группы разделили)?
Сделайте выводы: какими методами сегодня вы решали тригонометрические уравнения и какие знания вам для этого понадобились?
Методы:
Замена переменной и сведение к квадратному уравнению( явно заданные уравнения и неявные, но приводимые к ним с помощью основного тригонометрического тождества)
Разложение на множители (вынесение за скобку и группировка)
Это еще маленькая часть методов и знаний, с каждым уроком вы будете узнавать больше, расширяя свой кругозор, но всегда ищите способ применения ваших знаний к измененным условиям.
(слайд №16)
Собирайте свои знания по крупинкам копите их и тогда вы откроете для себя мир, где вы будете себя чувствовать комфортно и успешно и получать удовольствие от своей деятельности!
Творческое задание (Время зимнее, морозное и к сожалению некоторые наши сотрудники были вынуждены уйти на больничный. Но мы не имеем права на срыв работы или некачественное выполнение заданий, поэтому вам сейчас необходимо разработать алгоритмы решения уравнений, они должны быть настолько грамотными и доступными, что вы могли бы объяснить их даже по телефону, своим заболевшим сотрудникам.
Задание группам:
Составить алгоритм решения уравнений ,
Рефлексия:
Нам предстоит работа над следующим абсолютно новым для вас проектом, а сейчас просьба управляющим сдать оценочные листы, а всем сотрудникам, если вы удовлетворены собой, вам понравилась организация деятельности компаний и вы хотите сотрудничать с зарубежными партнерами по данным вопросам, просьба положить свою визитку в нашу общую визитницу!
Удачи вам, господа! Всего доброго!
Благодарю за сотрудничество!
Оценочный лист управляющих
| Фамилия, имя | вариант | результат |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценочный лист группы
| Фамилия, имя | Устная работа | Работа в группе | Индивиду альная работа | Средний балл за урок |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценки в баллах от 2 до 5






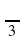 )=1,
)=1,  +2πn, n z,
+2πn, n z,  +2πn, n z.
+2πn, n z.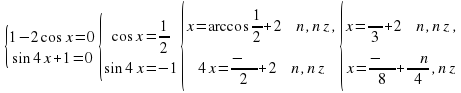
 ;
; 

 +
+ z
z +πn,
+πn, +
+ n z
n z










