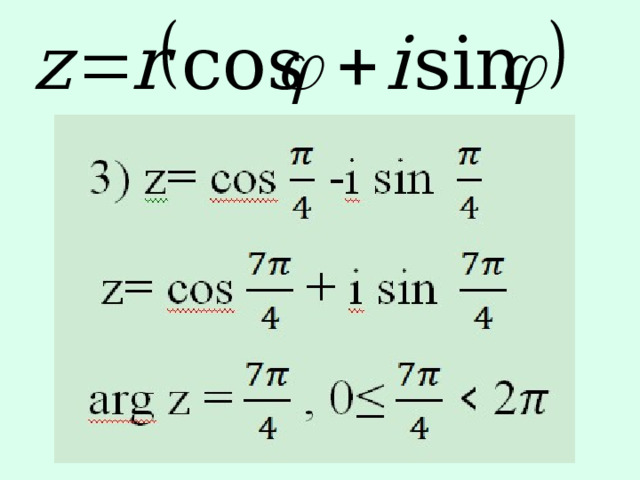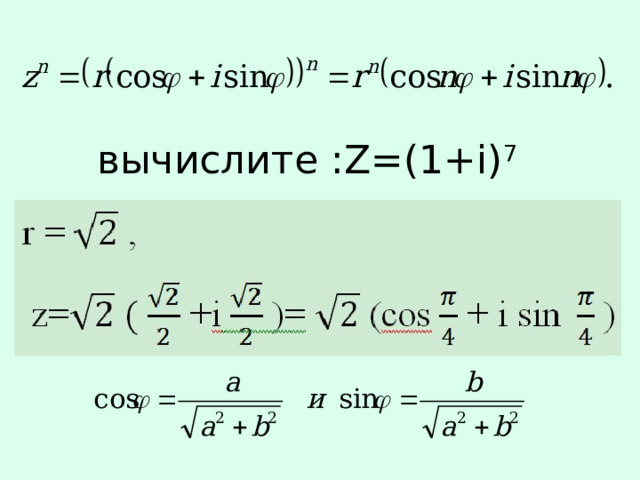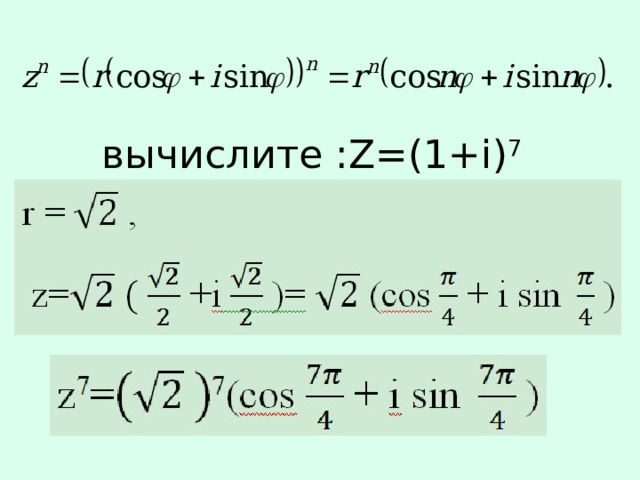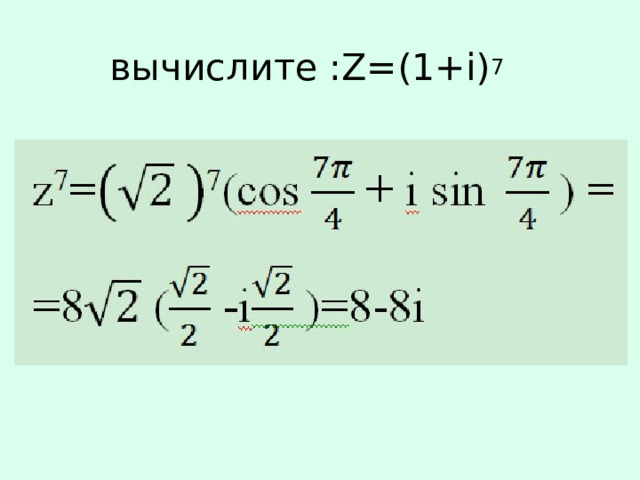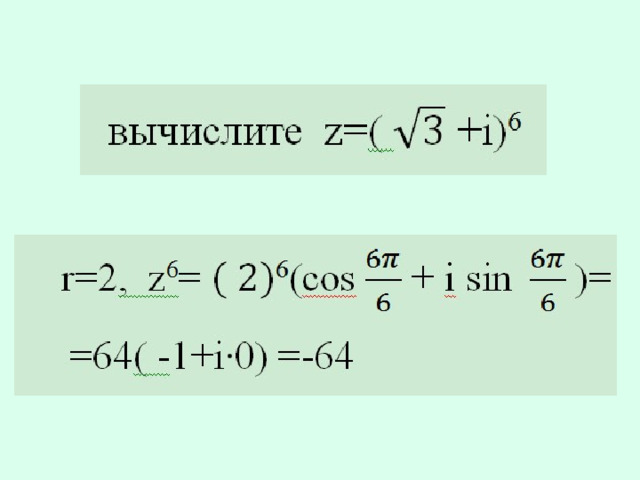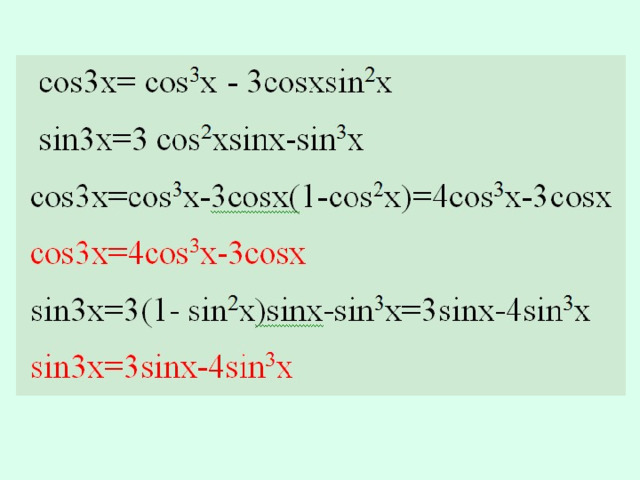Тригонометрическая и показательная формы комплексного числа

Комплексные числа Тригонометрическая форма комплексного числа Показательная форма комплексного числа

Подготовила:

учитель математики

ОБОУ « Лицей- интернат №1»

г.Курска

Белкина Е.Н.

Множество комплексных чисел- множество выражений вида a +bi, где a, b - действительные числа,i– мнимая единица, i=

a + 0i = а – комплексные числа данного вида отождествляют с действительным числом а

0 +bi = bi - комплексные числа данного вида называют мнимые числа

Обозначение комплексных чисел : z=a +bi, где а -действительная часть числа z ( Re z = a), число b называют мнимой частью числа z и обозначают Im z = b

Обозначение комплексных чисел : z=a +bi, где а -действительная часть числа z ( Re z = a), число b называют мнимой частью числа z и обозначают Im z = b

z=a +bi

Правую часть данного равенства называют алгебраической формой комплексного числа

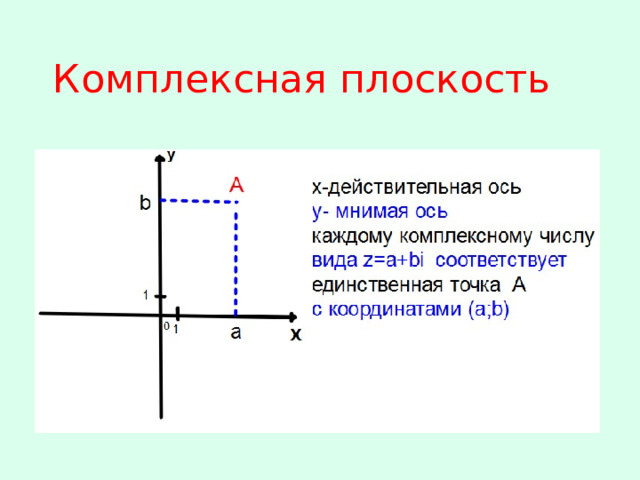
Комплексная плоскость

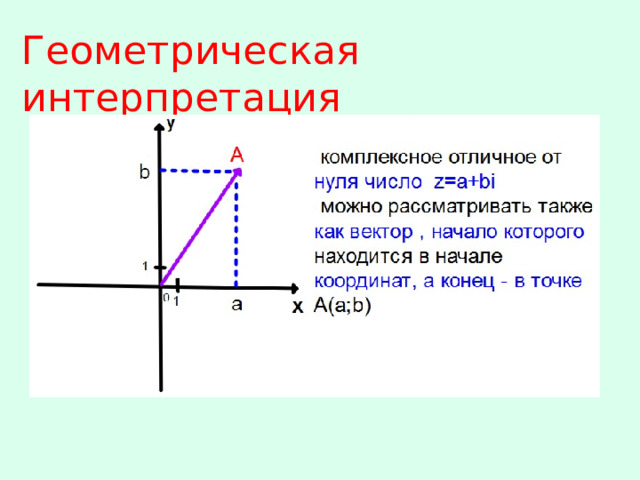
Геометрическая интерпретация

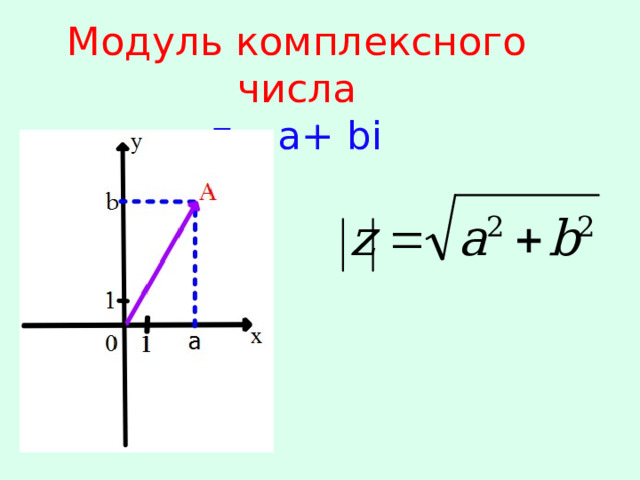
Модуль комплексного числа z= a+ bi

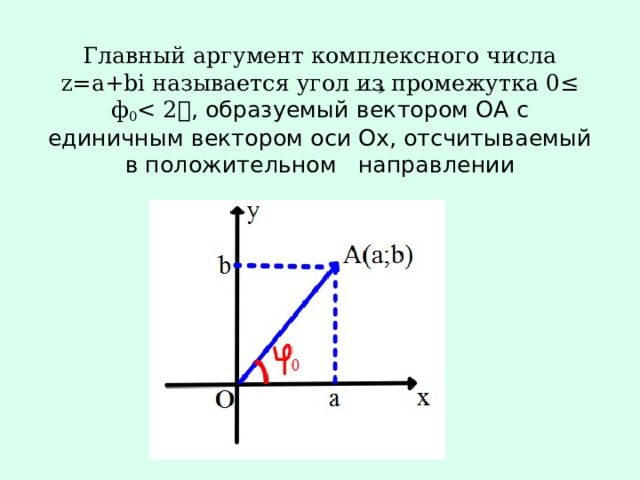
Главный аргумент комплексного числа z=a+bi называется угол из промежутка 0≤ ф 0

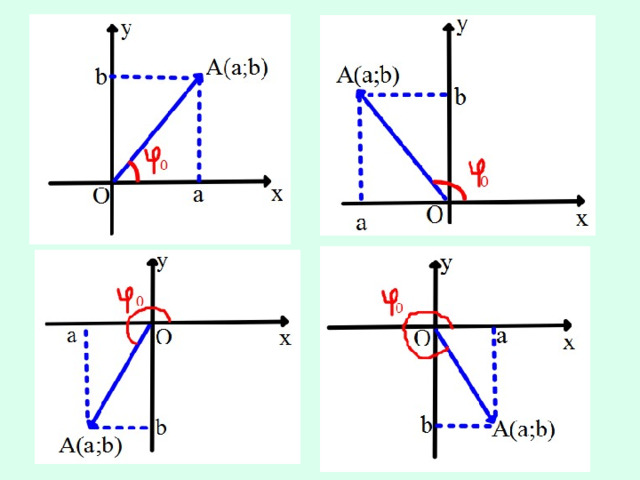
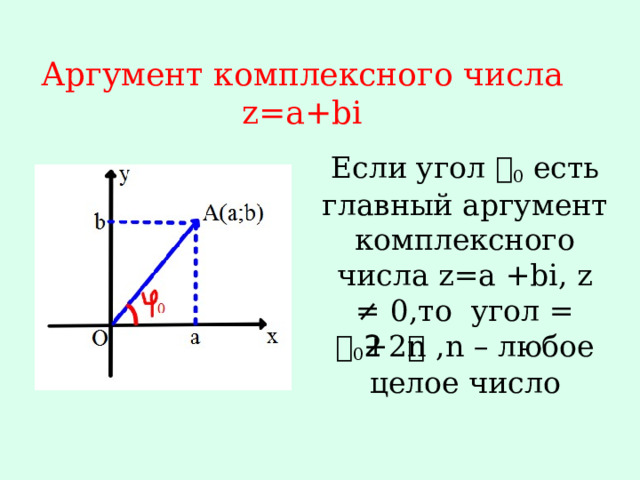
Аргумент комплексного числа z=a+bi

Если угол 𝝋 0 есть главный аргумент комплексного числа z=a +bi, z ≠ 0,то угол 𝝋= 𝝋 0 +2𝜋n ,n – любое целое число

Аргумент комплексного числа z=a+bi

z=a +bi, z ≠ 0,то угол 𝝋= 𝝋 0 +2𝜋n ,

n – любое целое число, можно найти как угол, одновременно удовлетворяющий двум равенствам :

Аргумент комплексного числа z=a+bi

Z=3+4i

тригонометрическая форма комплексного числа

где 𝝋 – аргумент комплексного числа,

r = - модуль комплексного числа,

тригонометрическая форма комплексного числа

тригонометрическая форма комплексного числа

тригонометрическая форма комплексного числа

тригонометрическая форма комплексного числа

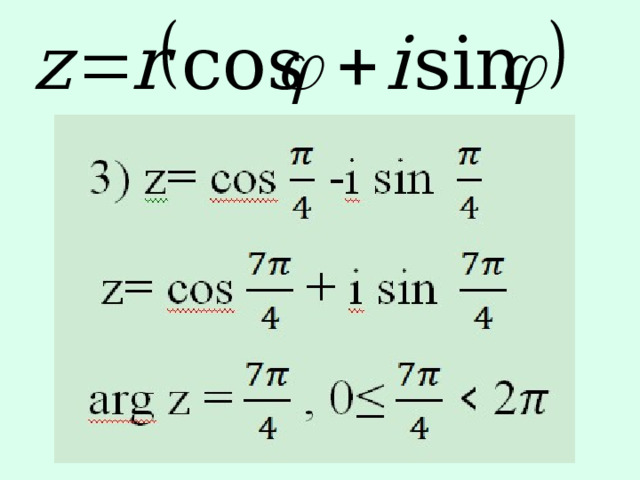
Умножение комплексных чисел

Частное комплексных чисел

(формула Муавра). Пусть z — любое отличное от нуля комплексное число, п — любое целое число.

Абраха́м де Муа́вр

  Английский математик французского  происхож-дения. Член Лондонского королевского общества, (Парижской и Берлинской академий наук. Ученик и помощник Исаака Ньютона. В 1722 году обнародовал фундаментальную формулу возведения в целую степень комплексных чисел

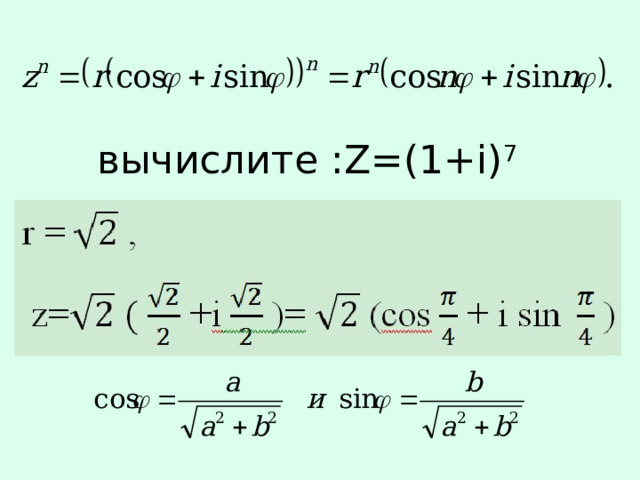
вычислите :Z=(1+i) 7

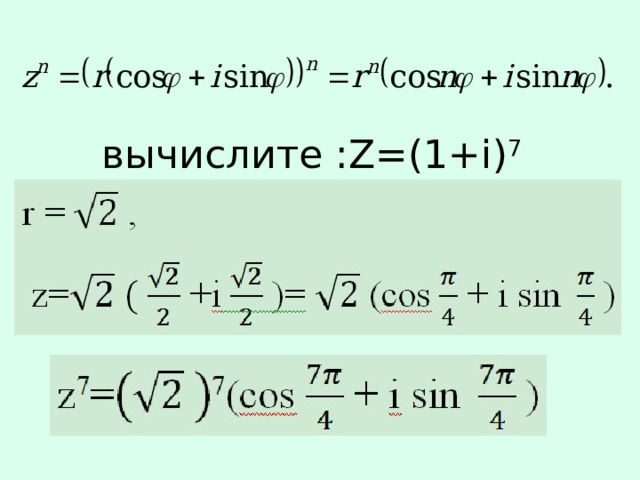
вычислите :Z=(1+i) 7

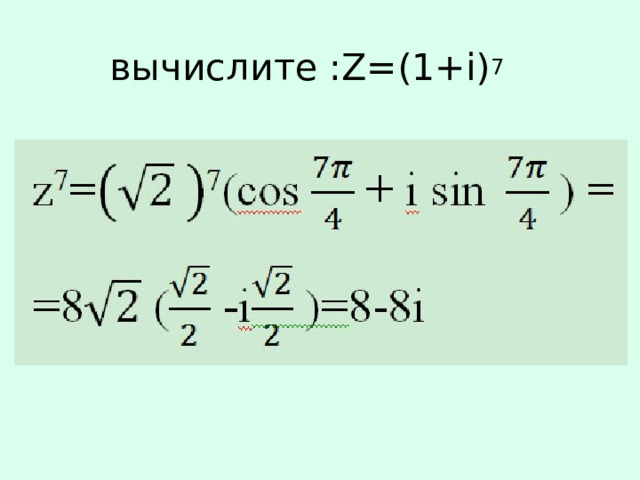
вычислите :Z=(1+i) 7

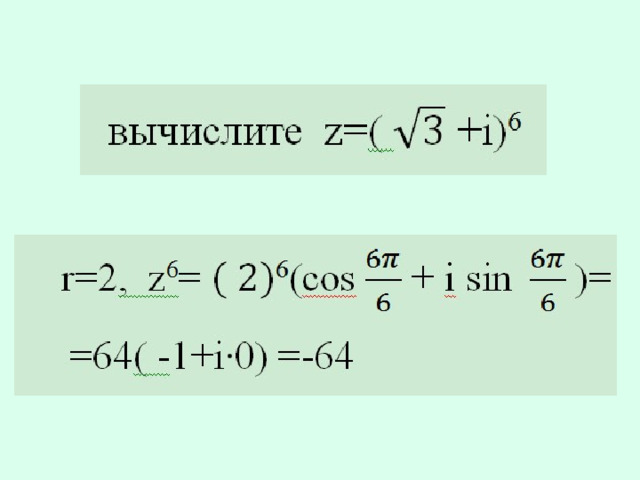
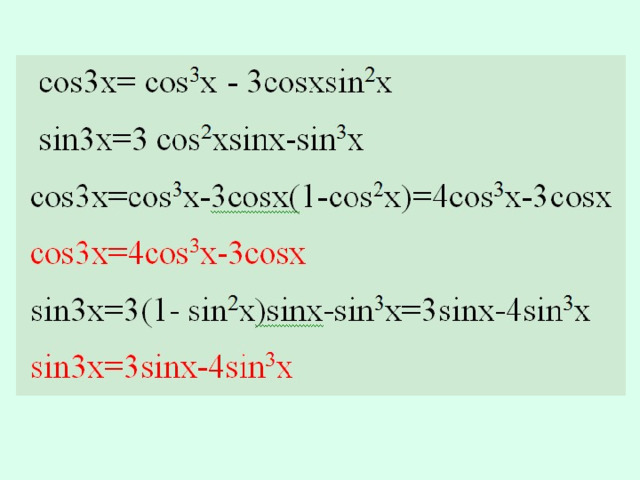
Извлечение корня из комплексного числа

Для любого натурального числа n и отличного от нуля комплексного числа z существуют n различных значений корня n-степени, n≥2

Формула Эйлера

Показательная форма комплексного числа

Физический смысл комплексных чисел

В настоящее время известен целый ряд таких физических величин, и комплексные числа применяются не только в математике, но также и в физике и технике ( теория упругости, электротехника, аэродинамика и т.д.

СПАСИБО ЗА ВНИМАНИЕ