Целые и рациональные числа. Действительные числа.

Урок 1/1 Дата _________________ Класс 10

Тема урока: Целые и рациональные числа. Действительные числа.

Тип урока: изучение нового материала

Цели урока: способствовать формированию знаний о числе (ввести понятия иррациональных, действительных чисел )

установить связь между множествами натуральных, целых, рациональных и действительных чисел

развивать навыки использования информационных технологий при изучении математики

воспитывать интерес к предмету через значение смысла числа

Оборудование урока: презентация, компьютер, проектор

Ход урока:

1. Организационный момент

2. Знакомство с предметом

- структура учебника

- единый орфографический режим

1. Изучение нового материала (презентация)

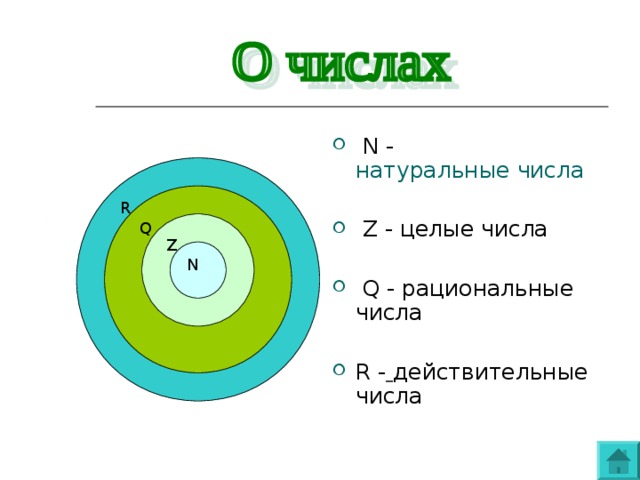
Изучение математики вы начали с натуральных чисел, т. Е. с чисел 1, 2, 3, 4, 5, … . При сложении и умножении натуральных чисел всегда получаются натуральные числа.

Однако разность и частное натуральных чисел могут не быть натуральными числами.

Дополнением натуральных чисел нулем и отрицательными (т. Е. числами, противоположными натуральным) образует множество целых чисел, т. Е. чисел 0, 1, -1, 2, -2, 3, -3, … . При сложении, вычитании и умножении целых чисел всегда получается целые числа.

Однако частное двух целых чисел может не быть целым числом.

Введение рациональных чисел, т. Е. чисел вида m/n, где m – целое число, n – натуральное число, позволило находить частное двух рациональных чисел при условии, что делитель не равен нулю. Каждое целое число m также является рациональным, так как его можно представить в виде m/1.

При выполнении четырех арифметических действии (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа.

Если рациональное число можно представить в виде дроби m/10^k, где m – целое число, k – натуральное число, то его можно записать в виде конечной десятичной дроби, Например, число 327/100 можно записать так: 3,27; число -23/10 можно записать так: -2,3.

Существуют рациональные числа, которые нельзя записать в виде конечной десятичной дроби, например 1/3, -2/9, 3/7. Если, например попытаться записать число 1/3 в виде десятичной дроби, используя известный алгоритм деления уголком, то получится бесконечная десятичная дробь 0,3333… . Бесконечную десятичную дробь 0,3333… называют периодической, повторяющуюся цифру 3 – ее периодом. Периодическую дробь 0,333… коротко записывают так: 0,(3); читается; «Ноль целых и три в периоде».

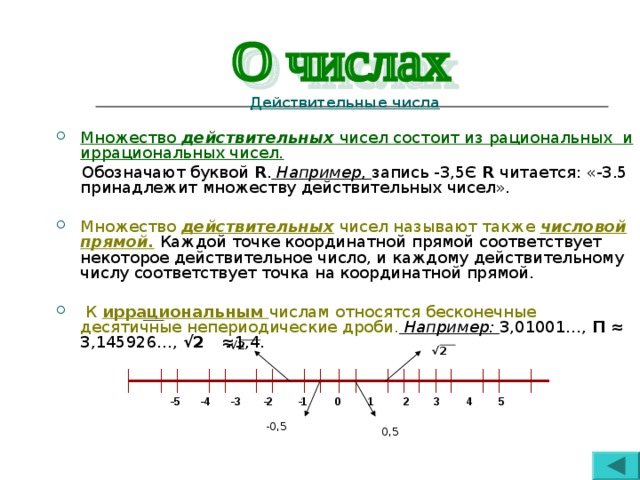
Числа, не являющиеся целыми и дробными называются иррациональными.

Так как любое рациональное число можно представить в виде бесконечной десятичной периодической дроби и любая бесконечная десятичная периодическая дробь представляет собой рациональное число, то каждое иррациональное число можно записать в виде бесконечной десятичной непериодической дроби и в свою очередь любая бесконечная десятичная непериодическая дробь – это иррациональное число.

Например, иррациональным числом является диагональ r квадрата со стороной, равной 1: 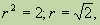а также число p = 3,14159… - отношение длины окружности к диаметру, постоянное для любой окружности.

Рациональные и иррациональные числа составляют множество действительных чисел (обозначается R). Каждому действительному числу соответствует единственная точка координатной прямой. Каждая точка координатной прямой соответствует единственному действительному числу: отрицательному (со знаком «-«), если она левее начала отсчета; положительному (со знаком «+»), если она правее начала отсчета. Множество действительных чисел называется также числовой прямой.

1. Закрепление изученного материала

• Работа с учебником выполнение нечетных заданий: №3, 9, 10, 12 (работа у доски и в тетради)

1. Итог урока

• Какие числа называются:

- натуральными?

- целыми?

- рациональными?

- действительными?

1. Домашнее задание §1,2 №№3(2,4), 9(4,6), №10 (2,4)

«Мысль выражать все числа девятью знаками, придавая им, кроме значения по форме, еще и значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна».

Пьер Симон Лаплас (1749-1827)

•   N - натуральные числа

•   Z - целые числа

•   Q - рациональные числа

• R - действительные числа

R

Q

Z

N

N - натуральные числа  

• Числа 1, 2, 3, …, употребляемые при счете предметов, образуют множество натуральных чисел .

Обозначают буквой N .

Например, запись 27Є N читается: «27 принадлежит множеству натуральных чисел».

• Любое натуральное число в десятичной системе счисления записывается с помощью цифр 0, 1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9.

Например, запись 2457 означает, что 2457=2•1000+4•100+5•10+7.

• Вообще если а - цифра тысяч, b –цифра сотен, d- цифра десятков и c- цифра единиц то имеем а • 1000+b•100+ c •10+d .

Используется также сокращенная запись аbcd.

1 2 3 4 5

Целые числа

• Натуральные числа, противоположные им числа и число нуль Составляют множество целых чисел. Обозначают буквой Z . Например , запись -27Є Z читается: «-27 принадлежит множеству целых чисел».

-5 -4 -3 -2 -1 0 1 2 3 4 5

Рациональные числа

• Целые и дробные числа ( положительные и отрицательные ) составляют множество рациональных чисел.

Обозначают буквой Q . Например, запись -3,5Є Q читается: «-3.5 принадлежит множеству рациональных чисел».

• Всякое рациональное число можно представить в виде дроби, m/n , где m Є Z , n Є N . Например: 5 =5/1=10/2=15/3, 0,7=7/10, -4=-4/1.

• Каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. Например: 5=5,000…, 1/8=0,125000…,1/3=0,333…,-5/11=0,4545…,-4,6=4,6000….

-5 -4 -3 -2 -1 0 1 2 3 4 5

- 0,5

0,5

Действительные числа

• Множество действительных чисел состоит из рациональных и иррациональных чисел.

Обозначают буквой R . Например, запись -3,5Є R читается: «-3.5 принадлежит множеству действительных чисел».

• Множество действительных чисел называют также числовой прямой. Каждой точке координатной прямой соответствует некоторое действительное число, и каждому действительному числу соответствует точка на координатной прямой.

• К иррациональным числам относятся бесконечные десятичные непериодические дроби. Например: 3,01001…, П ≈ 3,145926…, √2 ≈ 1,4.

-√2

√ 2

-5 -4 -3 -2 -1 0 1 2 3 4 5

-0,5

0,5

АЛГЕБРА и начала математического анализа 10 класс

Глава I. Действительные числа

Урок 1

Холодные числа, внешне сухие формулы математики полны внутренней красоты и жара сконцентрированной в них мысли. А.Д.Александров

Знания и навыки учащихся:

• знать, что такое натуральное, целое, рациональное число, периодическая дробь;
• уметь записывать бесконечную десятичную дробь в виде обыкновенной;
• уметь выполнять действия с десятичными и обыкновенными дробями.

§1 Целые и рациональные числа

1. Множество натуральных чисел

N = {1; 2; 3;…}

• сумма и произведение нат.чисел являются числами натуральными

• разность и частное – могут не быть натуральными числами

7 + 7 = 14

12 – 7 = 5

7 – 7 =0

7 – 12 = -5

2. Множество целых чисел

Z = {…, -3; -2; -1; 0; 1; 2; 3;…}

• сумма, разность и произведение целых чисел всегда являются целыми числами

5 + (-7) = -2

-7 – 7 = -14

• частное – может не быть целым числом

7 · (– 12) = -5

-7 : (-7)= 1

5 : (– 7) = -5 7

3. Множество рациональных чисел

• сумма, разность, произведение и частное (кроме деления на нуль) над рациональными числами всегда являются рациональными числами

4. Каждое рациональное число можно представить в виде бесконечной периодической десятичной дроби

Целое число

Конечная десятичная дробь

Период равен нулю 12, 000…= 12,(0)

где m – целое число , k – натуральное число

Бесконечная периодическая десятичная дробь

Период равен нулю 2,75000…=2,75(0 )

Период равен 2

№ 1. Запишите в виде десятичной дроби:

Сверим ответы:

№ 2. Выполните действия и запишите результат в виде десятичной дроби:

Сверим ответы:

5. Справедливо и обратное утверждение: каждая бесконечная периодическая десятичная дробь является рациональным числом

Рассмотрим задачу 2 из параграфа и составим алгоритм : представить бесконечную периодическую десятичную дробь 0,2(18) в виде обыкновенной

1)Нужно умножить дробь на 10 n , где n – количество десятичных знаков , содержащихся в записи этой дроби до периода

Получаем х ·10 n

1) Пусть х = 0,2(18 )

Умножая на 10, получим

х·10 = 2,1818…

2) Умножая обе части последнего равенства на 100, получим

1000х=218,1818…

2)Нужно умножить дробь на 10 k , где k – количество цифр в периоде:

Получаем х ·10 n · 10 k = х ·10 n+k

• (2) – (1), получим

990х = 216

х= 216/990 , сокращая

х = 12/55

3) Отнять от равенства (2) равенство (1),

Решить полученное уравнение

№ 3 (1,3,5,6). Записать в виде обыкновенной дроби бесконечную десятичную дробь:

1) 0,(6) =

Сверим ответы:

Далее №4; №5(1 )

№ 3. Записать в виде обыкновенной дроби бесконечную десятичную дробь:

3) 0,1(2) =

ко один

обе час-

х=

Сверим ответы:

Далее №4; №5(1 )

№ 3. Записать в виде обыкновенной дроби бесконечную десятичную дробь:

5) -3,(27) =

Сверим ответы:

Далее №4; №5(1 )

№ 3. Записать в виде обыкновенной дроби бесконечную десятичную дробь:

6) -2,3(82)=

Сверим ответы:

Далее №4; №5(1 )

Ответы:

= 4,75

Ответы:

§ 1 , разобрать задачу 3 (стр.6);

№ 1 (2, 4, 6),

№ 2 (2, 4, 6),

№ 3 (2, 4),

№ 5 (2).

Домашнее задание

• Множества каких чисел вы знаете?
• Приведите примеры этих чисел.
• Что такое периодическая дробь?
• Как записать её в виде обыкновенной?

Итоги урока №1

Глава1 , §1

10 класс

Домашняя работа.

11

0,7272

Глава1 , §1; 1(2,4,6)

10 класс

Глава1 , §1; 2(2,4,6)

х = - 8/9

Глава1 , §1; 3(2,4)

Глава1 , §1; 5(2)