Основы алгебры логики
Основным понятием математической логики является понятие высказывания. Под высказыванием понимают повествовательное предложение, о котором имеет смысл говорить, что оно истинно или ложно.
Определение 1. Отрицанием высказывания А называется такое высказывание 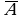 ( читается «не А», «неверно, что А» ), которое истинно тогда и только тогда, когда А ложно.
( читается «не А», «неверно, что А» ), которое истинно тогда и только тогда, когда А ложно.
Например, отрицанием высказывания А: «6 делится на 2» является высказывание 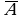 : «неверно, что 6 делится на 2» (или «6 не делится на 2»).
: «неверно, что 6 делится на 2» (или «6 не делится на 2»).
Для пояснения логических операций удобно использовать так называемые таблицы истинности (истинностные таблицы):
| [A] | [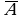 ] ] |
| 1 0 | 0 1 |
Определение 2. Конъюнкцией высказываний А и В называется высказывание А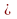 В (читается «А и В», «А конъюнкция В»), которое истинно тогда и только тогда, когда истинны оба высказывания А и В.
В (читается «А и В», «А конъюнкция В»), которое истинно тогда и только тогда, когда истинны оба высказывания А и В.
Например, конъюнкцией высказываний А: «24» и В: «6 – простое число» является высказывание А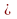 В: «24 и 6 – простое число», которое ложно, поскольку ложным является высказывание В. Истинностная таблица для конъюнкции имеет вид:
В: «24 и 6 – простое число», которое ложно, поскольку ложным является высказывание В. Истинностная таблица для конъюнкции имеет вид:
| [A] | [B] | [AÙB] |
| 1 1 0 0 | 1 0 1 0 | 1 0 0 0 |
Определение 3. Дизъюнкцией высказываний А и В называется высказывание А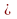 В (читается «А или В», «А дизъюнкция В»), которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний А или В.
В (читается «А или В», «А дизъюнкция В»), которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний А или В.
Союз «или» в данном случае носит неразделительный смысл, поскольку высказывание А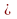 В истинно и при истинности обоих высказываний А и В. Например, высказывание «4¹13 или 7 – простое число» истинно, так как является дизъюнкцией двух истинных высказываний «4¹13» и «7 – простое число». Дизъюнкции соответствует следующая таблица истинности:
В истинно и при истинности обоих высказываний А и В. Например, высказывание «4¹13 или 7 – простое число» истинно, так как является дизъюнкцией двух истинных высказываний «4¹13» и «7 – простое число». Дизъюнкции соответствует следующая таблица истинности:
| [A] | [B] | [AÚB] |
| 1 1 0 0 | 1 0 1 0 | 1 1 1 0 |
Определение 4. Импликацией высказываний А и В называется высказывание А В (читается «если А, то В», «из А следует В», «А влечет В», «А импликация В»), которое ложно тогда и только тогда, когда высказывание А истинно, а В ложно. Истинностная таблица для импликации такова:
В (читается «если А, то В», «из А следует В», «А влечет В», «А импликация В»), которое ложно тогда и только тогда, когда высказывание А истинно, а В ложно. Истинностная таблица для импликации такова:
| [A] | [B] | [A→B] |
| 1 1 0 0 | 1 0 1 0 | 1 0 1 1 |
В импликации А В высказывание А называется посылкой (или условием), а высказывание В – заключением. Между посылкой и заключением могут отсутствовать причинно-следственные связи, но это не может повлиять на истинность или ложность импликации. Поэтому с точки зрения логики, допустимы, например, такие импликации: «если диагонали ромба пересекаются под прямым углом, то Ю.Гагарин – великий русский поэт», «если город Брянск расположен на берегу Невы, то 3+2=4». В первом случае импликация, согласно определению, является ложной, а во втором – истинной. То обстоятельство, что в случае, когда ложна посылка, импликация будет истинной независимо от истинностного значения заключения, кратко формулируют так: «из ложного следует все, что угодно».
В высказывание А называется посылкой (или условием), а высказывание В – заключением. Между посылкой и заключением могут отсутствовать причинно-следственные связи, но это не может повлиять на истинность или ложность импликации. Поэтому с точки зрения логики, допустимы, например, такие импликации: «если диагонали ромба пересекаются под прямым углом, то Ю.Гагарин – великий русский поэт», «если город Брянск расположен на берегу Невы, то 3+2=4». В первом случае импликация, согласно определению, является ложной, а во втором – истинной. То обстоятельство, что в случае, когда ложна посылка, импликация будет истинной независимо от истинностного значения заключения, кратко формулируют так: «из ложного следует все, что угодно».
Определение 5. Эквиваленцией высказываний А и В называется высказывание А В (читается «А тогда и только тогда, когда В», «А необходимо и достаточно для В», «А эквиваленция В»), которое истинно тогда и только тогда, когда истинностные значения А и В совпадают.
В (читается «А тогда и только тогда, когда В», «А необходимо и достаточно для В», «А эквиваленция В»), которое истинно тогда и только тогда, когда истинностные значения А и В совпадают.
Например, высказывание «2+7=8 тогда и только тогда, когда 3» истинно,
поскольку оно является эквиваленцией двух ложных высказываний «2+7=8» и «3». Таблица истинности для эквиваленции имеет вид :
| [A] | [B] | [A↔B] |
| 1 1 0 0 | 1 0 1 0 | 1 0 0 1 |
Замечание. Высказывания А и В называются равносильными, если их истинностные значения совпадают. Если высказывания А и В равносильны, то пишут А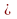 В. Нетрудно проверить, что
В. Нетрудно проверить, что 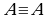 ; если
; если 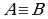 , то
, то 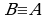 ; из
; из 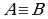 и
и 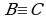 следует
следует 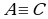 , для любых высказываний А, В и С. Это означает, что отношение равносильности на множестве высказываний является отношением эквивалентности.
, для любых высказываний А, В и С. Это означает, что отношение равносильности на множестве высказываний является отношением эквивалентности.
Теорема 2. Для равносильности формул логики высказываний выполняются следующие свойства:
(1) 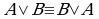 ; (1')
; (1') 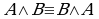 — коммутативность;
— коммутативность;
(2) 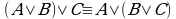 ; (2')
; (2') 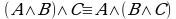 — ассоциативность;
— ассоциативность;
(3) 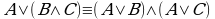 ; (3')
; (3') 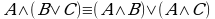 — дистрибутивность;
— дистрибутивность;
(4) 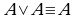 ; (4')
; (4') 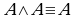 — идемпотентность;
— идемпотентность;
(5) 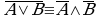 ; (5')
; (5') 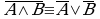 — законы де Моргана;
— законы де Моргана;
(6) 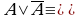 И; (6')
И; (6') 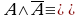 Л — закон исключения третьего;
Л — закон исключения третьего;
(7) 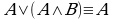 ; (7')
; (7') 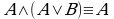
(8) 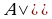 И
И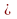 И; (8')
И; (8') 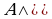 Л
Л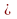 Л — законы поглощения;
Л — законы поглощения;
(9) 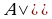 Л
Л 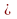
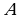 ; (9')
; (9') 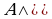 И
И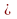
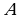
(10) 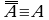 — закон двойного отрицания;
— закон двойного отрицания;
(11) 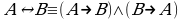 — исключение эквиваленции;
— исключение эквиваленции;
(12) 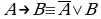 — исключение импликации.
— исключение импликации.
Доказательство. Все свойства доказываются с помощью таблиц истинности.
Задачи для тренировки:
Логическая функция F задаётся выражением ¬a (b ¬c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
| ? | ? | ? | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы.
Логическая функция F задаётся выражением (a b) (a ¬c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
| ? | ? | ? | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы.
Логическая функция F задаётся выражением (a b) (a ¬c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
| ? | ? | ? | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы.
Логическая функция F задаётся выражением (a ¬c) (¬b ¬c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
| ? | ? | ? | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы.
Логическая функция F задаётся выражением (a ¬c) (¬b ¬c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
| ? | ? | ? | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы.
Логическая функция F задаётся выражением (a ¬c) (¬a b c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
| ? | ? | ? | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы.
Ответы







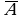 ( читается «не А», «неверно, что А» ), которое истинно тогда и только тогда, когда А ложно.
( читается «не А», «неверно, что А» ), которое истинно тогда и только тогда, когда А ложно. 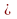 В (читается «А и В», «А конъюнкция В»), которое истинно тогда и только тогда, когда истинны оба высказывания А и В.
В (читается «А и В», «А конъюнкция В»), которое истинно тогда и только тогда, когда истинны оба высказывания А и В.  В (читается «если А, то В», «из А следует В», «А влечет В», «А импликация В»), которое ложно тогда и только тогда, когда высказывание А истинно, а В ложно. Истинностная таблица для импликации такова:
В (читается «если А, то В», «из А следует В», «А влечет В», «А импликация В»), которое ложно тогда и только тогда, когда высказывание А истинно, а В ложно. Истинностная таблица для импликации такова: В (читается «А тогда и только тогда, когда В», «А необходимо и достаточно для В», «А эквиваленция В»), которое истинно тогда и только тогда, когда истинностные значения А и В совпадают.
В (читается «А тогда и только тогда, когда В», «А необходимо и достаточно для В», «А эквиваленция В»), которое истинно тогда и только тогда, когда истинностные значения А и В совпадают.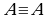 ; если
; если 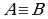 , то
, то 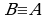 ; из
; из 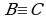 следует
следует 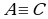 , для любых высказываний А, В и С. Это означает, что отношение равносильности на множестве высказываний является отношением эквивалентности.
, для любых высказываний А, В и С. Это означает, что отношение равносильности на множестве высказываний является отношением эквивалентности. 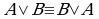 ; (1')
; (1') 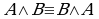 — коммутативность;
— коммутативность;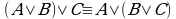 ; (2')
; (2') 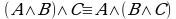 — ассоциативность;
— ассоциативность;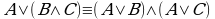 ; (3')
; (3') 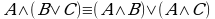 — дистрибутивность;
— дистрибутивность; 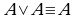 ; (4')
; (4') 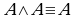 — идемпотентность;
— идемпотентность;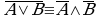 ; (5')
; (5') 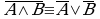 — законы де Моргана;
— законы де Моргана;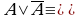 И; (6')
И; (6') 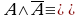 Л — закон исключения третьего;
Л — закон исключения третьего;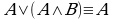 ; (7')
; (7') 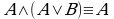
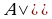 И
И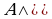 Л
Л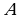 ; (9')
; (9') 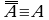 — закон двойного отрицания;
— закон двойного отрицания;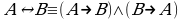 — исключение эквиваленции;
— исключение эквиваленции;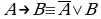 — исключение импликации.
— исключение импликации.









