Туундулар жонундо

Дифференциальное исчисление функции одной переменной

Дифференциальное исчисление – раздел математики, в котором изучаются производные и дифференциалы функций и их применение к исследованию функций .

§ Производная функции

Определение производной функции. Необходимое условие существования производной

Пусть y   =   f ( x ) определена в точке x 0 и некоторой её окрестности.

Придадим x 0 приращение  x такое, что x 0   +    x  D ( f ) .

Функция при этом получит приращение

 f ( x 0 )   =   f ( x 0   +    x )   –   f ( x 0 )   .

ОПРЕДЕЛЕНИЕ. Производной функции y   =   f ( x ) в точке x 0 называется предел отношения приращения функции в этой точке к приращению аргумента  x , при  x      0 (если этот предел существует и конечен), т.е.

Обозначают:

Производной функции y   =   f ( x ) в точке x 0 справа ( слева ) называется

( если этот предел существует и конечен ).

Обозначают:

– производная y   =   f ( x ) в точке x 0 справа,

– производная y   =   f ( x ) в точке x 0 слева.

ТЕОРЕМА (необходимое и достаточное условие существо - вания производной).

Функция y   =   f ( x ) имеет производную в точке x 0  в этой точке существуют и равны между собой производные функции справа и слева. Причем

ТЕОРЕМА (необходимое условие существования производ - ной функции в точке).

Если функция y   =   f ( x ) имеет производную в точке x 0 , то функция f ( x ) в этой точке непрерывна.

Замечание . Непрерывность функции в точке x 0 не является достаточным условием существования в этой точке производной функции.

Например, функция y   =   |   x   | непрерывна на всей области опре- деления, но не имеет производной в точке x 0  = 0.

Определение. Пусть функция f( x ) определена на (a,b) и непрерывна в т. x 0 из этого промежутка (a,b) . Тогда приращению   x отвечает приращение  y = f( x 0 +  x ) – f( x 0 ) . Если приращение  y может быть представлено в виде суммы линейной относительно  x б.м.ф и б.м.ф высшего порядка малости относительно  x :  y = А .  x + О (  x ) (А= const) то функцию f( x ) называют дифференцируемой в точке x 0 .

А .  x – дифференциал функции f( x ) в точке x 0

Обозначают:

Теорема . Функция дифференцируема в точке т. и т.т., когда она имеет производную в этой точке. Следствие.

Геометрический смысл дифференциала Дифференциал функции в точке равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента.

Соответствие x 0      f    ( x 0 ) является функцией, определенной на множестве D 1  D ( f ).

Операцию нахождения для функции y   =   f ( x ) её производной функции называют дифференцированием функции f ( x ).

  УПРАЖНЕНИЕ. Доказать по определению, что

( sin x )      =  cos x , ( cos x )      =   – sin x ,  x  ℝ

( e x )      =  e x , ( a x )      =   a x     ln a ,  x  ℝ

Физический и геометрический смысл производной

1) Физический смысл производной .

Если функция y   =   f ( x ) и её аргумент x являются физическими величинами, то производная f    ( x ) – скорость изменения величины y относительно величины x  .

ПРИМЕРЫ.

а) Пусть S   =   S ( t ) – расстояние, проходимое точкой за время t .

Тогда производная S    ( t 0 ) – скорость в момент времени t 0 .

б) Пусть q   =   q ( t ) – количество электричества, протекающее через поперечное сечение проводника в момент времени t .

Тогда q    ( t 0 ) – скорость изменения количества электричества в момент времени t 0 , т.е. сила тока в момент времени t 0 .

в) Пусть m   =   m ( x ) – масса отрезка [ a   ;   x ].

Тогда m    ( x ) – скорость изменения массы в точке x 0 , т.е. линейная плотность в точке x 0 .

2) Геометрический смысл производной.

Пусть ℓ – некоторая кривая, M 0 – точка на кривой ℓ .

Любая прямая, пересекающая ℓ не менее чем в двух точках , называется секущей .

Касательной к кривой ℓ в точке M 0 называется предельное положение секущей M 0 M 1 , если точка M 1 стремится к M 0 , двигаясь по кривой .

Очевидно, что если касательная к кривой в точке M 0 существует, то она единственная.

Рассмотрим кривую y   =   f ( x ).

Пусть в точке M 0 ( x 0   ;   f ( x 0 )) она имеет невертикальную касатель- ную M 0 N .

Таким образом, получили: f    ( x 0 ) – угловой коэффициент касательной к графику функции y   =   f ( x ) в точке M 0 ( x 0   ;   f ( x 0 )).

( геометрический смысл производной функции в точке ).

 Уравнение касательной к кривой y   =   f ( x ) в точке M 0 ( x 0   ;   f ( x 0 )) можно записать в виде

Замечания .

1) Прямая, проходящая через точку M 0 перпендикулярно касательной, проведенной к кривой в точке M 0 , называется нормалью к кривой в точке M 0 .

Т.к. для угловых коэффициентов перпендикулярных прямых справедливо равенство k 1      k 2   =   –1   , то уравнение нормали к y   =   f ( x ) в точке M 0 ( x 0   ;   f ( x 0 )) будет иметь вид

, если f    ( x 0 )    0.

Если же f    ( x 0 ) = 0, то касательная к кривой y   =   f ( x ) в точке M 0 ( x 0   ;   f ( x 0 )) - горизонтальная прямая, уравнение которой

y  =  f ( x 0 ),

а нормаль – вертикальная прямая, уравнение которой x   =   x 0 .

2) Пусть кривая y   =   f ( x ) имеет в точке M 0 ( x 0   ;   f ( x 0 )) вертикальную касательную M 0 N  ,    – угол наклона секущей M 0 M 1 к Ox .

Таким образом, если кривая y   =   f ( x ) имеет в точке M 0 ( x 0   ;   f ( x 0 )) вертикальную касательную , то функция y   =   f ( x ) не имеет в точке x 0 производной .

Так как в соседних с M 0 точках кривая y   =   f ( x ) имеет касательные и их угол наклона к оси Ox стремится к 90  при  x      0, то x 0 является для функции f ( x ) точкой разрыва II рода , причем

Правила дифференцирования

1) Производная постоянной функции равна нулю , т.е.

C      =   0, где С – константа.

2) Производная суммы ( разности ) равна сумме ( разности ) производных , т.е.

• Производная произведения находится по правилу :

Замечание . Формула дифференцирования произведения может быть легко обобщена на случай большего числа множителей. Например,

, где С – константа.

Говорят: «постоянный множитель выносится за знак производной».

5) Производная дроби находится по правилу :

6) Если функция  ( t ) имеет производную в точке t , а функция f ( u ) имеет производную в точке u   =    ( t ) , то сложная функция y   =   f (  ( t )) имеет производную в точке t , причем

(правило дифференцирования сложной функции).

7) ТЕОРЕМА ( о производной обратной функции).

Пусть функция y   =   f ( x ) имеет производную в точке x 0 , причем f    ( x 0 )    0 . Если существует обратная функция x  =    ( y ) , то она имеет производную в точке y 0   =   f ( x 0 ) и

УПРАЖНЕНИЯ.

1) Зная, что ( sin x )      =  cos x , ( cos x )      =   – sin x , ( e x )      =  e x , получить формулы

2) Используя теорему о производной обратной функции, доказать, что

По определению и с помощью правил дифференцирования

находят производные основных элементарных функций (таблица производных).

Производная любой элементарной функции находится с помощью таблицы производных

и правил дифференцирования.

Производные высших порядков

§ Теоремы о среднем значении для дифференцируемых функций Условия монотонности функции

Необходимое условие существования экстремума функции

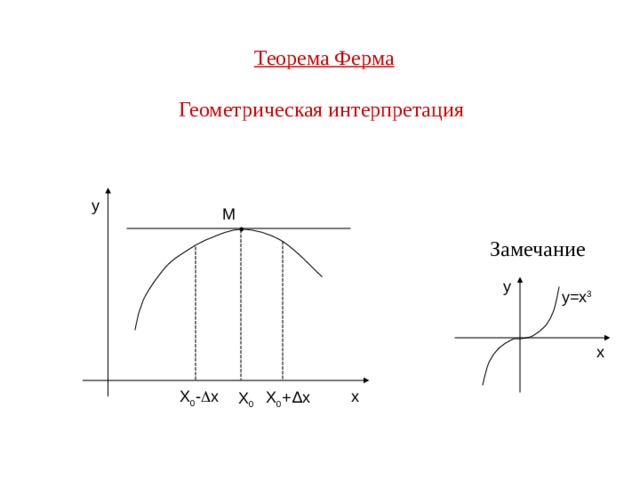
Теорема Ферма Геометрическая интерпретация

y

M

Замечание

y

y=x 3

x

X 0 -  x

x

X 0 + Δ x

X 0

m y y M m b a x b a x " width="640"

Теорема Ролля

Пусть функция y=f(x) а) непрерывна на отрезке [ a, b ] б) дифференцируема на интервале ( a, b ) в) f( a ) = f( b ) Тогда найдется хотя бы одна точка С ∈ ( a, b ), такая, что f ' ( С ) = 0

Возможные случаи

или

f(a)=f(b)

f(a)=f(b)m

y

y

M

m

b

a

x

b

a

x

Теорема Лагранжа (о конечных приращениях)

Пусть функция y = f( x ) а) определена и непрерывна на отрезке [ a, b ] б) дифференцируема на интервале ( a, b ). Тогда найдется хотя бы одна точка С ∈ ( a, b ), такая, что

y

Геометрически

B

f(b)-f(a)

A



b - a

tg  =f ' (C)

C 1

C

C 2

b

a

x

Теорема Коши

Пусть функции f( x ) и g( x ) а) непрерывны на отрезке [ a, b ] б) дифференцируемы на интервале ( a, b ) и g ' ( x ) ≠ 0. Тогда найдется хотя бы одна точка С ∈ ( a, b ), такая, что

Теоремы Ролля, Лагранжа, Коши

§ Теорема Лопиталя (правило Лопиталя)

Пусть функции f(x) и g(x) дифференцируемы в окрестности точки x = a и g ' (x) ≠ 0 в окрестности x=a . Если и существует , то существует конечный предел , причем

Замечание 1 . Если f' (x) и g' (x) удовлетворяют условиям теоремы Лопиталя, в окрестности точки x=a , то правило Лопиталя применяется к отношению производных:

Замечание 2 . Правило Лопиталя применимо и в случае x →∞ , т.е. если

Теорема. ( Правило Лопиталя для случая ∞ / ∞ ) Пусть функции f(x) и g(x) а) дифференцируемы в окрестности точки x = a б) в) g ' (x) ≠ 0 в окрестности x=a .

г)

тогда существует конечный предел , причем

Правило Лопиталя

Правило Лопиталя

§ Формула Тейлора и Маклорена

Определение. Многочленом (полиномом) n - го порядка называется функция P n ( x ) = a 0 + a 1 x + a 2 x 2 + … + a n x n где a 0 , a 1 , …, a n – коэффициенты многочлена, n – натуральные числа. Многочлен полностью определяется своими коэффициентами.

Определение. Многочленом (полиномом) по степеням ( x – x 0 ) называется функция P n ( x ) = a 0 + a 1 ( x – x 0 ) + a 2 ( x – x 0 ) 2 + … + a n ( x – x 0 ) n .

Определение. Формула называется формулой Тейлора для многочлена P n (x) .

Теорема. Пусть функция f ( x ) определена на интервале ( a, b ) , имеет в точке x ∈ (a, b) производные до n - го порядка включительно. Тогда при x → x 0 функция f(x) сходится к своему многочлену Тейлора и можно записать f ( x ) = f ( x 0 ) + f ‘ ( x 0 )( x – x 0 ) + f ‘‘ ( x 0 )( x – x 0 ) 2 + … + f (n) ( x 0 )( x – x 0 ) n +R n ( x ) .

Формула называется формулой Тейлора для функции f ( x ) .

Теорема. Разность между функцией f ( x ) и её многочленом Тейлора P ( x ) является б.м. функцией высшего порядка малости по сравнению с ( x – x 0 ) n f ( x ) – P ( x ) = R n ( x ) = O ( ( x – x 0 ) n )

R n ( x ) - о статочный член

в форме Пеано R n ( x ) = O ( ( x – x 0 ) n )

в форме Лагранжа , где x 0 

f(x)=P(x)+R n (x)

y

y=f(x)

R n (x)

f(x)

P(x)

x 0

x

x

Формула Маклорена – частный случай формулы Тейлора при x 0 = 0

P 2 (x)

P 3 (x)

y

P 1 (x)

P 4 (x)

sinx

- π

π

0

x

Стандартные разложения Маклорена

Уметь получать разложения

f(x 2 ); c ) невозрастающей на ( a,b ), если ∀ x 1 , x 2 ∈( a,b ) при x 1 x 2 f(x 1 ) ≥ f(x 2 ) ; а) неубывающей на ( a,b ), если ∀ x 1 , x 2 ∈( a,b ) при x 1 x 2 f(x 1 ) ≤ f(x 2 ) . Пример невозрастающей функции y f(x 1 )= f(x 2 ) f(x 3 ) y=f(x) x 1 2 3 x " width="640"

§ ПОЛНОЕ ИССЛЕДОВАНИЕ ФУНКЦИИ Определение. Функция y=f(x) называется а) возрастающей на ( a,b ), если ∀ x 1 , x 2 ∈( a,b ) при x 1 x 2 f(x 1 ) 2 ); b ) убывающей на ( a,b ), если ∀ x 1 , x 2 ∈( a,b ) при x 1 x 2 f(x 1 )f(x 2 ); c ) невозрастающей на ( a,b ), если ∀ x 1 , x 2 ∈( a,b ) при x 1 x 2 f(x 1 ) ≥ f(x 2 ) ; а) неубывающей на ( a,b ), если ∀ x 1 , x 2 ∈( a,b ) при x 1 x 2 f(x 1 ) ≤ f(x 2 ) .

Пример невозрастающей функции

y

f(x 1 )= f(x 2 ) f(x 3 )

y=f(x)

x 1 2 3

x

x 0 – противоположный . Определение. Точки, в которых f '(x) =0 называются стационарными точками. Определение. Точки, в которых f '(x) =0 или не существует, называются критическими точками. Возможные варианты стационарных и критических точек y y стационарные f '(x) =0 y критические f '(x) критические f '(x) экстр. нет экстр. экстр. экстр. нет экстр. нет экстр. x 0 x 0 x x 0 x 0 x x x 0 x 0 " width="640"

Определение. Говорят, что f '(x) меняет знак в точке x 0 , если существует

окрестность точки x 0 : ( x 0 - δ , x 0 + δ ), в которой при xf '(x) сохраняет один знак,

а при xx 0 – противоположный .

Определение. Точки, в которых f '(x) =0 называются стационарными точками.

Определение. Точки, в которых f '(x) =0 или не существует, называются

критическими точками.

Возможные варианты стационарных и критических точек

y

y

стационарные f '(x) =0

y

критические f '(x)

критические f '(x)

экстр.

нет экстр.

экстр.

экстр.

нет экстр.

нет экстр.

x 0

x 0

x

x 0

x 0

x

x

x 0

x 0

0 - в x 0 минимум. " width="640"

Теорема. ( 1 ый Достаточный признак существования экстремума )

Пусть y=f(x) непрерывна в интервале, содержащем критическую точку x 0 , дифференцируема во всех точках этого интервала, кроме может быть самой x 0 , тогда

а) если при переходе слева направо через x 0 производная f ' (x) меняет знак с «+» на «-», то в точке x 0 функция f(x) имеет максимум;

b ) если знак производной меняется с «-» на «+», то в точке x 0 функция f(x) имеет минимум.

Теорема. ( Второй достаточный признак существования экстремума )

Если в критической точке x 0 функции y=f(x) обращается в ноль не только первая производная, но и все последующие до (n-1)- й включительно, т.е.

f ' (x 0 ) = f '' (x 0 ) = f ''' (x 0 ) =…= f ( n-1 ) (x 0 )=0, а f ( n ) (x 0 ) ≠ 0 ,

тогда x 0 будет точкой экстремума , если n – четное ; x 0 не будет точкой экстремума, если n – нечетное .

Характер экстремума определяется знаком f ( n ) (x 0 )≠0 .

При f ( n ) (x 0 ) 0 - в x 0 максимум, при f ( n ) (x 0 ) 0 - в x 0 минимум.

0 , то кривая на ( a, b ) вогнута. " width="640"

Выпуклость, вогнутость, точки перегиба

y

Определение. Кривая обращена выпуклостью вверх на ( a,b ) , если

все точки кривой лежат ниже любой ее касательной на ( a,b ) .

Кривая называется выпуклой .

x

a b x

y

Определение. Кривая обращена выпуклостью вниз на ( a,b ) , если

все точки кривой лежат выше любой ее касательной на этом интервале.

Кривая называется вогнутой .

x

a b x

Теорема. ( Достаточное условие выпуклости и вогнутости кривой )

Пусть y = f (x) непрерывна на [ a,b ] , и имеет в ( a, b ) производную до второго порядка включительно , тогда

а) если во всех точках интервала ( a, b ) вторая производная функции f (x) отрицательна: f '' (x) 0 , то кривая на ( a, b ) выпукла;

b ) если во всех точках интервала вторая производная положительна:

f '' (x) 0 , то кривая на ( a, b ) вогнута.

x 0 - по другую сторону касательной. y x x Следствие из достаточного условия выпуклости и вогнутости кривой . ( Необходимое условие существования точки перегиба ) Если вторая производная в некоторой точке x 0 равна нулю или не существует , то эта точка есть точка перегиба графика функции. Теорема. ( Достаточное условие существования точки перегиба ) Пусть в точке x 0 выполнены необходимые условия существования точки перегиба, и пусть при переходе через эту точку f '' (x) меняет знак , тогда точка x 0 является точкой перегиба графика функции. " width="640"

Определение. Точка ( x 0 ;y 0 ), лежащая на кривой f(x) , называется точкой перегиба функции y=f(x) , если существует окрестность точки x 0 такая, что при x x 0 кривая лежит по одну сторону касательной, при x x 0 - по другую сторону касательной.

y

x

x

Следствие из достаточного условия выпуклости и вогнутости кривой . ( Необходимое условие существования точки перегиба )

Если вторая производная в некоторой точке x 0 равна нулю или

не существует ,

то эта точка есть точка перегиба графика функции.

Теорема. ( Достаточное условие существования точки перегиба )

Пусть в точке x 0 выполнены необходимые условия существования точки перегиба, и пусть при переходе через эту точку f '' (x) меняет знак , тогда точка x 0 является точкой перегиба графика функции.

Асимптоты кривых

y

Определение. Прямая называется асимптотой кривой y = f ( x ) , если расстояние от точки M кривой f ( x ) до данной прямой → 0 при неограниченном удалении т. М от начала координат.

O

x

f(x)

M

Опр. Прямая x = a называется вертикальной асимптотой графика функции f(x) , если хотя бы один из пределов равен ∞ или - ∞ .

Опр. Прямая y = k x + b называется наклонной асимптотой графика функции f ( x ) при x → ± ∞, если

Теорема. ( Критерий существования наклонной асимптоты )

Для того, чтобы прямая y = k x + b была наклонной асимптотой, необходимо и достаточно, чтобы существовали пределы

Общий план исследования функции и построения графиков

• D(y) – область непрерывности
• Найти, охарактеризовать точки разрыва, выделить вертикальные асимптоты
• Четность, нечетность
• Периодичность
• Промежутки возрастания, убывания; точки min, max
• Промежутки выпуклости, вогнутости; точки перегиба
• Наклонные асимптоты графика функции
• Дополнительные точки: 1) пересечение с осями координат 2) f(x min ), f(x max ) 3) f(x перегиб )
• Построение графика функции