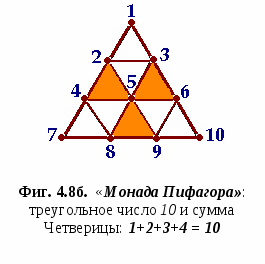Творческая работа "Тетраксис"

Содержание:

1. Вступление………………………………………………………………….3

2. Тетраксис как мистический символ………………………………………3

3. Тетраксис в геометрии……………………………………………………..5

3.1. Способы построения тетраксиса………………………………………...5

4. Геометрия тетраксиса…………………………………………………….10

5. Тетраксис как геометрический инструмент…………………………….12

6. Создание узоров в тетраксисе. Цветок жизни………………………….14

7. Выводы……………………………………………………………………15

Литература……………………………………………………………...……16

1. Вступление.

Одним из древнейших символов, способных оказывать прямое воздействие на объекты и события считается тетраксис. Древние Пифагорейцы употребляли этот символ в своих клятвах. Вот, например, одна из них «...Клянусь именем Тетраксис, ниспосланным нашим душам. В нем источник и корни вечно цветущей Природы...» Видим, что этот символ для древних имел исключительное значение. Египтяне же считали его символом верховных сил. Пройдя сквозь века, тетраксис не утратил своей актуальности и в наши дни. Тетраксис представляет интерес не только как мистический символ, но и как геометрическая фигура. Эта работа посвящена изучению тетраксиса и его свойств – великого творения Пифагора.

Цель работы: изучить понятие тетраксис, рассмотреть возможности использования тетраксиса как универсального инструмента для некоторых геометрических построений.

Задачи:

Изучить литературу по данной теме;

Изучить историю появления и развития понятия «тетраксис»;

Изготовить модель тетраксиса;

Изучить возможности изготовленной модели для геометрических построений.

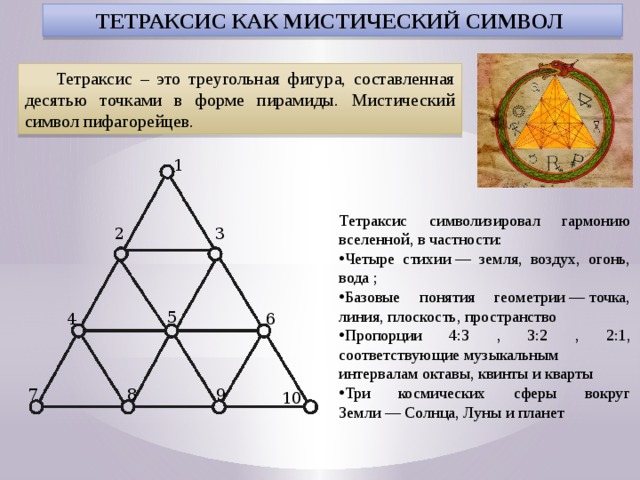
1. Тетраксис как мистический символ.

Интернет-энциклопедия «Википедия» дает нам такое определение тетраксиса:

Тетарксис – это треугольная фигура, составленная десятью точками в форме пирамиды. Мистический символ пифагорейцев.

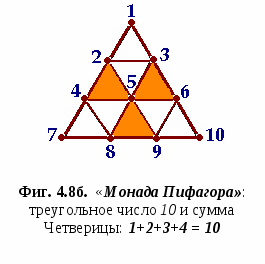
В схеме Тетрактиса единица означает точку, двойка – протяженность, тройка (треугольник) – плоскость, четверка – объемность или пространство. Тетрактис делится десятью точками пересечения линий на девять равносторонних треугольников, олицетворяющих собой Всемирную полноту.

Тетрактис – чрезвычайно распространенный символ, его можно встретить в древних манускриптах, алхимических трактатах, на фасадах зданий и соборов, исторически связанных с тамплиерами и масонами. Он имел множетсво модификаций – его перестраивали, усекали, лишая вершины – активности, изымали ряд точек или добавляли новые, и каждая из таких манипуляций со столь универсальным знаком имела определённые реализационные последствия. Изображение тетраксиса есть на стене Аккерманской крепости в городе Белгород-Днестровский. Огромный треугольник, расположенный на одной из стен башен, обращенной к лиману, является одним из самых загадочных архитектурных элементов крепости. Сама фигура состоит из десяти вмонтированных в кладку каменных ядер. Расположенный на одном из самых видных мест крепости, данный архитектурный элемент продолжает будоражить внимание изучающих его исследователей, не разгадавших его тайну до сих пор.

Таких изображений очень много видов. Объяснить изобилие изображений очень просто. Существует четыре канонических изображений тетраксиса. Каждое каноническое изображение – это символ определенной области знаний. В которую был посвящен ученик Пифагора. Условно эти области знаний можно разделить на геометрию, инфологию, философию и веру.

1. Тетраксис в геометрии

Тетраксис, в геометрическом смысле – это десять точек, образующих равносторонний треугольник. В своей работе я буду рассматривать способы построения тетраксиса и его геометрические свойства.

Если быть точнее, то тетраксис – это совокупность десяти точек, вписанных в равносторонний треугольник таким образом, что соседние точки равноудалены друг от друга. Изображение, демонстрирующее определения тетраксиса:

1. Способы построения тетраксиса

Способов нарисовать тетраксис множество. В своей работе я буду рассматривать самые простые из них.

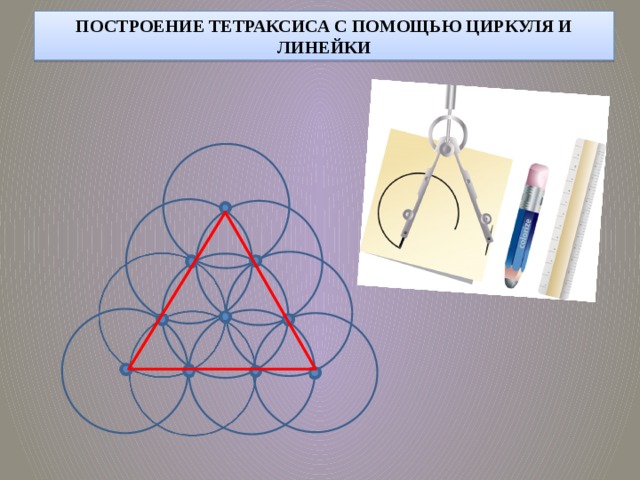
Построим тетраксис с помощью циркуля и линейки. 2500 лет назад Пифагор и его известные ученики использовали этот метод для построения тетраксиса.

Возьмём обычный циркуль, лист бумаги и начнем. Рисуем первую точку. Помещаем в эту точку иглу циркуля и проводим окружность. Радиус окружности определяем сами. Главное условие, на протяжении всего процесса, пока мы не закончим тетраксис, расстояние между ножками циркуля должно быть неизменным. Теперь на окружности выбираем произвольную точку, отмечаем ее, делаем центром второй окружности.

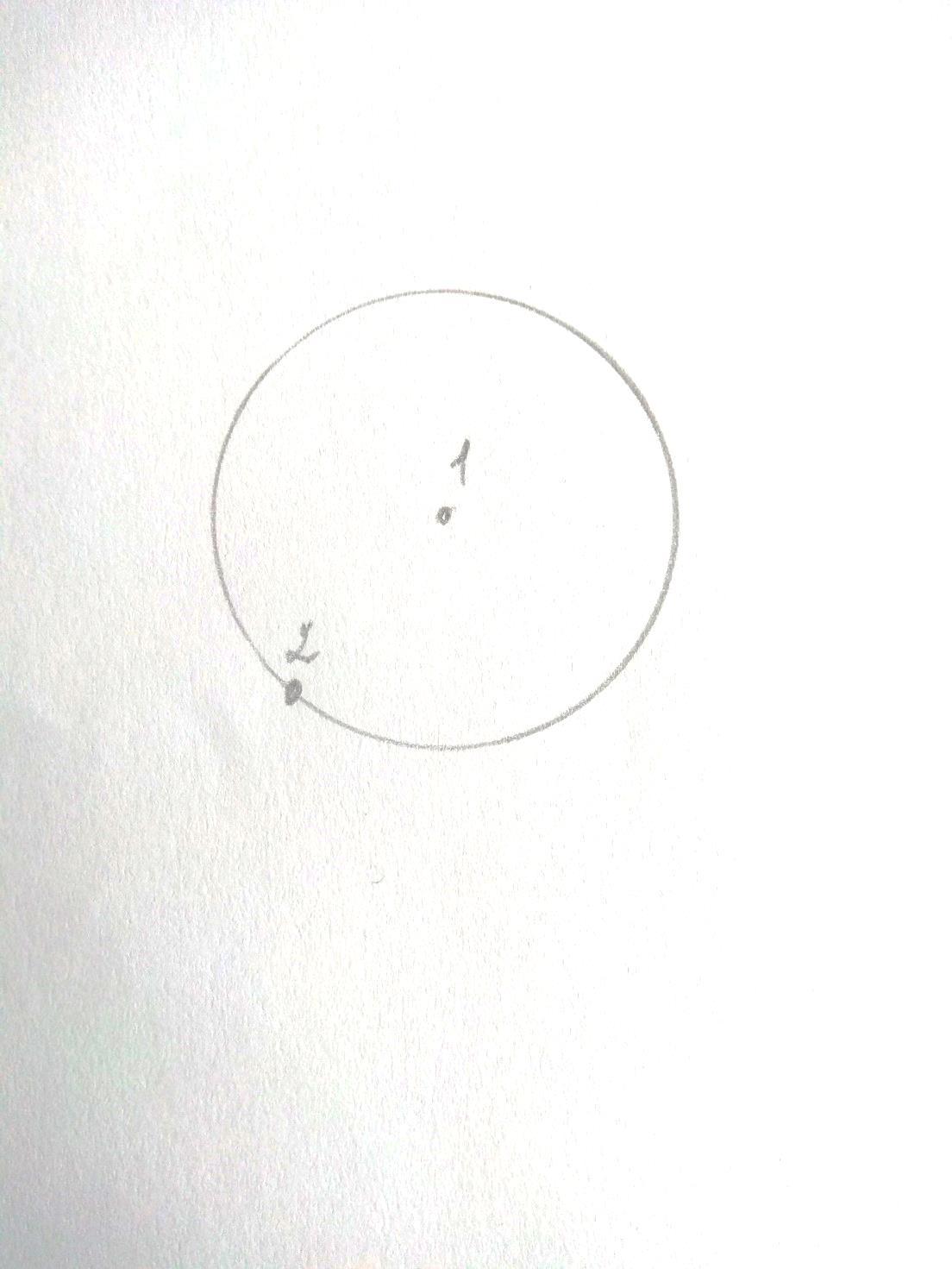
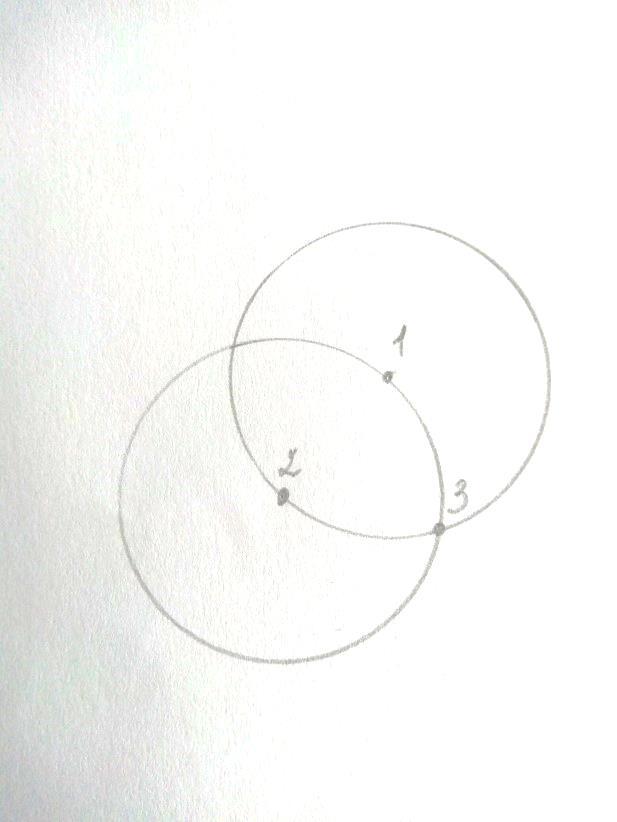
В том месте, где наши окружности пересекутся, прорисовываем третью точку. Строим еще одну окружность с центром в третьей точке…

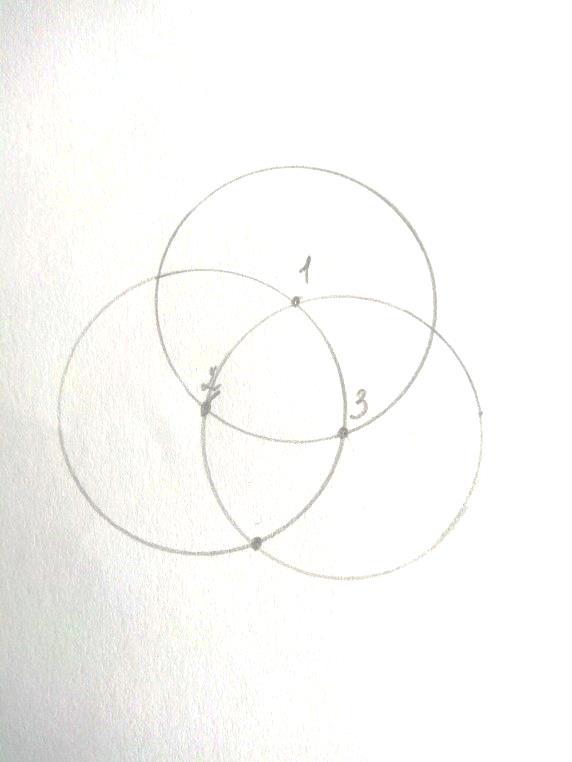
Дальше следуем алгоритму, пересечение окружностей – точка. Точка центр окружности.

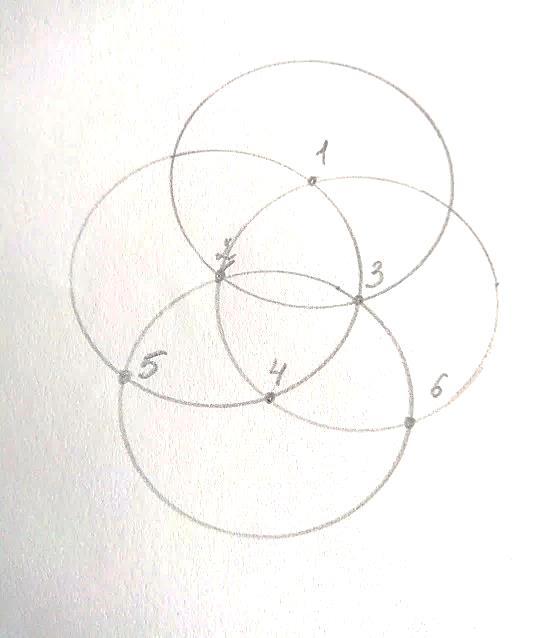
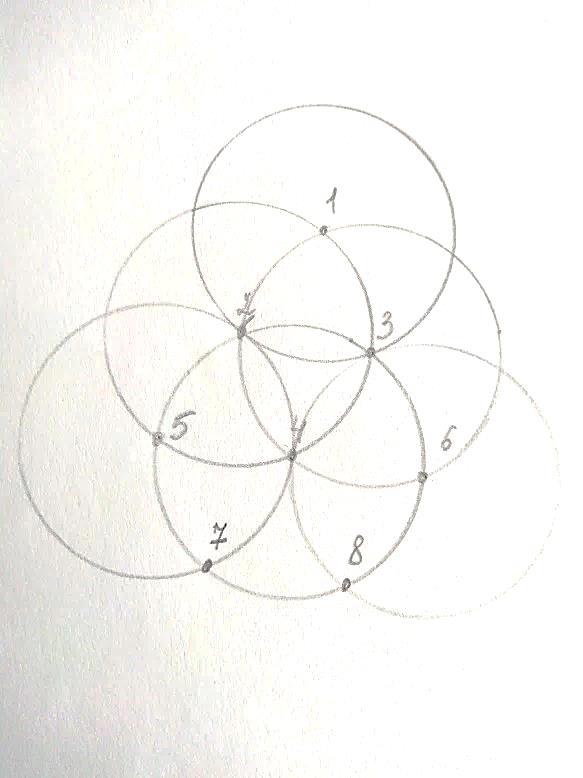
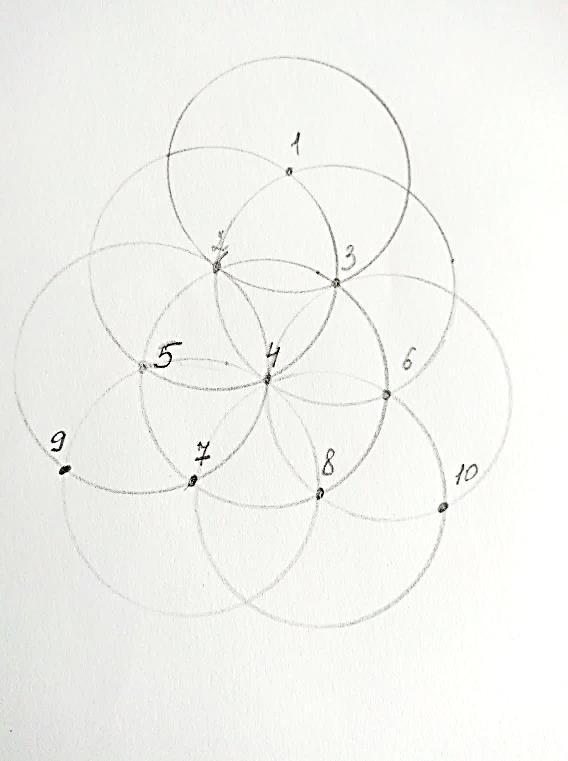
Получаем тетраксис – десять точек, вписанных в равносторонний треугольник,так, что соседние две точки равноудалены.

Проверяем правильность рисунка, точки 2,3,5,6,7,8 должны принадлежать одной окружности, с центром в точке 4, а если нарисовать вторую окружность, с тем же центром (4) и радиусом, например 4-9, тогда образовавшаяся окружность пройдет через точки 1, 9, 10. Стоит отметить, что данный способ построения тетраксиса, самый правильный, классический.

Тетраксис можно построить и более простым способом, но этот способ нельзя назвать строго геометрическим, так как для построения используется шкала линейки.

Итак, рисуем тетраксис циркулем и линейкой.

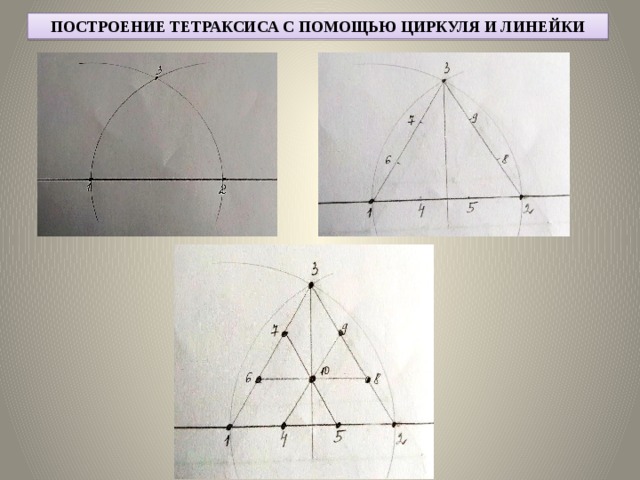
Нарисуем прямую линию. Обозначим концы линии точками 1,2 – это наше основание. Теперь при помощи циркуля нарисуем две окружности с центрами в концах нашего отрезка и радиусом равным длине отрезка. Обозначим точку пересечения окружностей – это вершина 3.

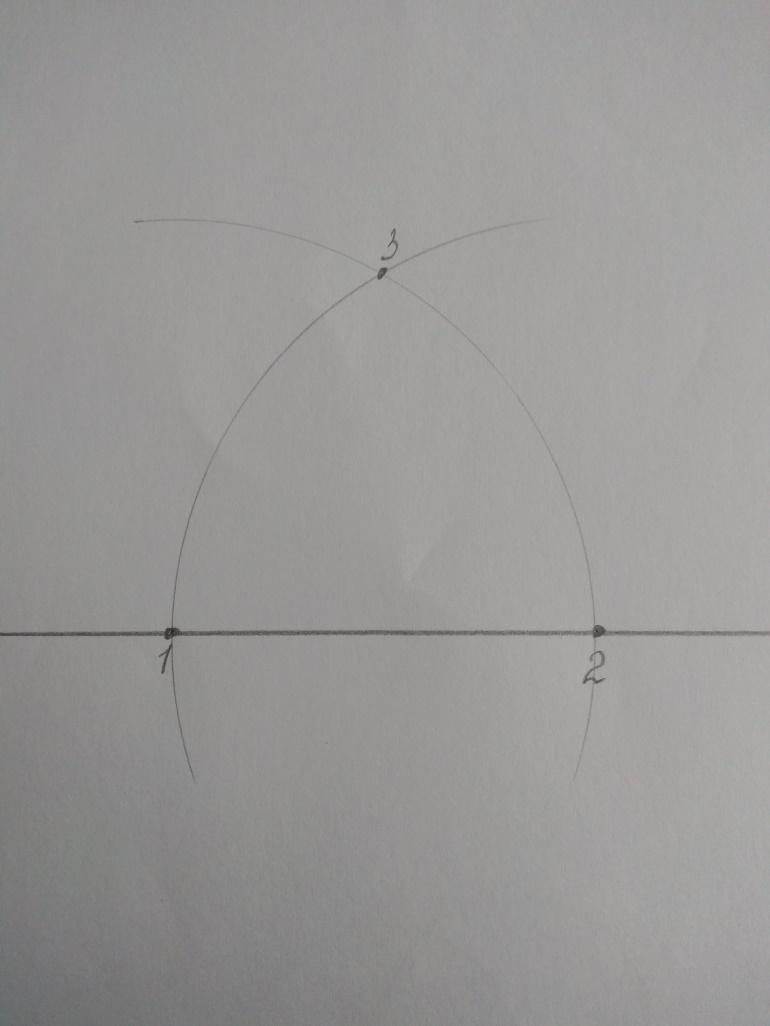
Соединим все три точки прямыми линиями, получился равносторонний треугольник. Теперь при помощи линейки делим каждую сторону на 3 равные части и отмечаем полученные отрезки точками.

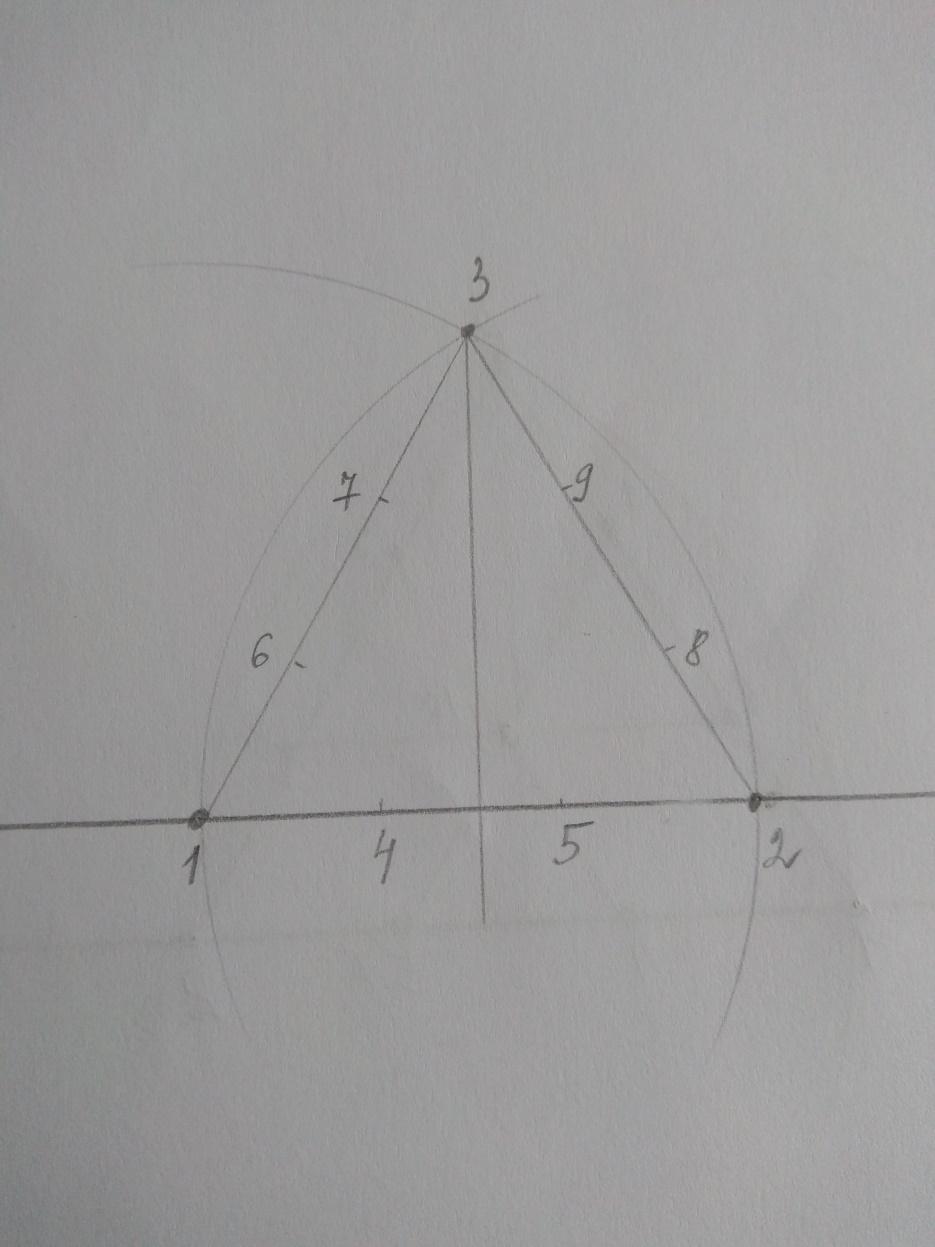
Остается построить центральную точку. Проводим от вершины перпендикуляр к основанию и соединяем точки третьего ряда, место пересечения перпендикуляра и линии соединяющей точки (голубые линии на рисунке) и есть искомый центр 10.

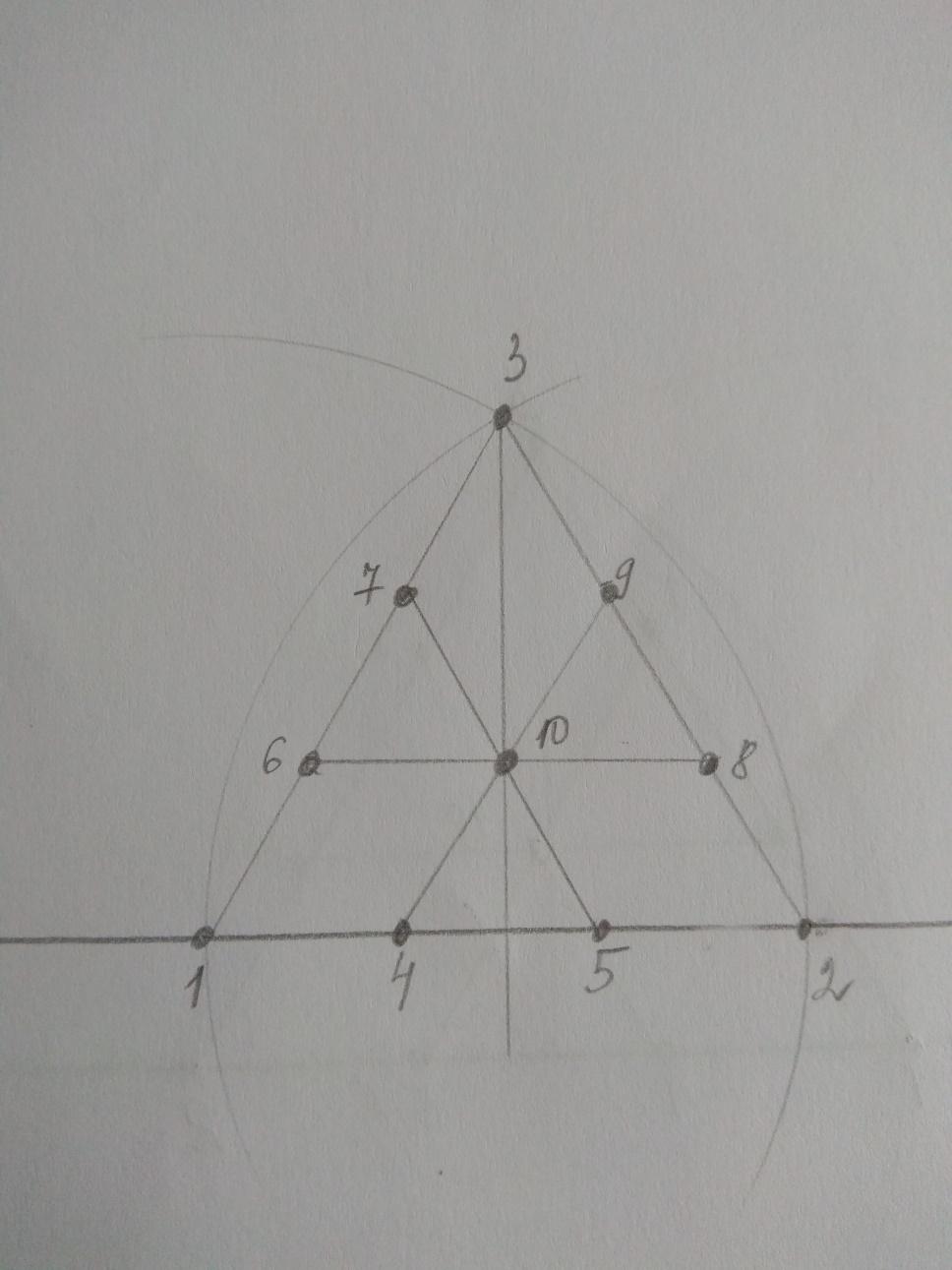
Проверим правильность рисунка, соединим точки 5-7 и 4-9 , отрезки должны пересечься в точке 10.

1. Геометрия тетраксиса. Рисуем в тетраксисе

Нарисуем для начала тетраксис. На фото вы можете видеть, что у меня получилось. Выясним, какие геометрические фигуры могут образовывать точки тетраксиса.

Для этого я соединила все точки, принадлежащие тетраксису всеми возможными способами. Сразу стало видно, что отрезки, соединяющие точки тетраксиса, образуют множество известных геометрических фигур. Это множество различных треугольников, параллелограммы, трапеции, шестиугольник, различные виды углов, параллельные и перпендикулярные прямые.

Если мы расставим на плоскости десять точек так, чтобы они образовывали тетраксис, то мы с легкостью можем построить любую из перечисленных фигур. Это можно увидеть на следующих иллюстрациях:

1. Построение параллельных и перпендикулярных прямых:

1. Построение различных углов:

1. Построение различных треугольников:

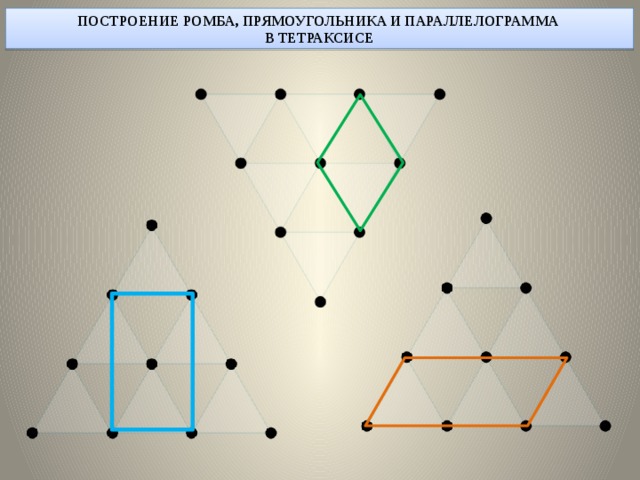
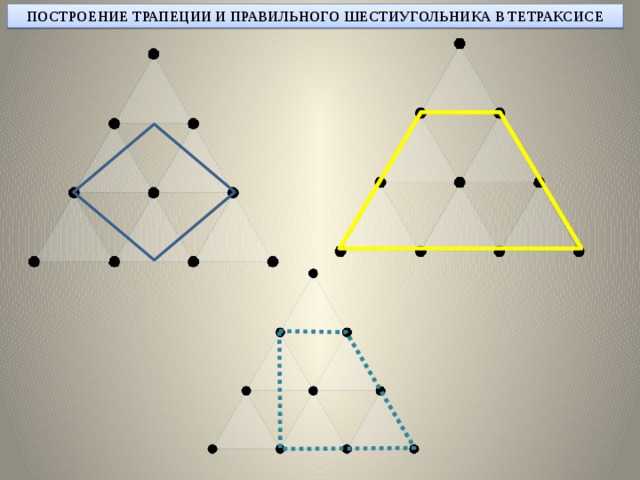
1. Построение параллелограмма, прямоугольника, трапеции, шестиугольника:

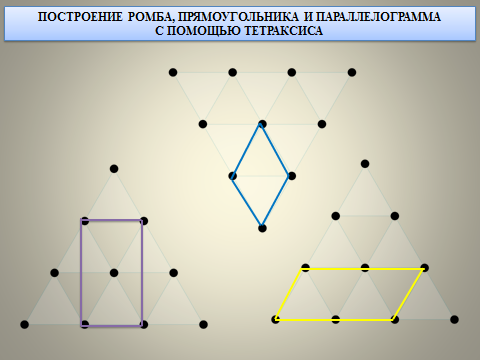
Чтобы сделать рисунок геометрической фигуры в тетраксисе, решаем, что мы хотим нарисовать. Например — треугольник.

У него три вершины, значит нам потребуются три точки, не лежащие на одной прямой. Выбираем три точки и соединяем их прямыми линиями. Аналогично для любой другой фигуры.

1. Тетраксис как геометрический инструмент

Видим, что точки, образующие тетраксис, могут образовывать множество геометрических фигур. Я решила изготовить тетраксис с целью использования его в качестве геометрического инструмента. Для этого я построила тетраксис на плотном листе бумаги. Нанесла 10 основных точек. С одной стороны тетраксиса я наклеила пленку, для того, чтобы он мог свободно скользить по поверхности бумаги для удобства построений. Все точки я соединила отрезками всеми возможными способами. В основных десяти точках я проделала отверстия – маленькие дырочки. Для того, чтобы построить ту или иную геометрическую фигуру, её нужно визуально наметить в самом тетраксисе и нанести на бумагу вершины этой фигуры через отверстия тетраксиса, затем соединить вершины, используя вместо линейки край тетраксиса.

Вот, что у меня получилось.

С помощью тетраксиса можно изображать не только многоугольники, но и окружность. Приняв за центр окружности центральную точку тетраксиса, отметим его на листе бумаги . Прижмем пальцем к бумаге центр, установит карандаш в любую другую точку тетраэдра ( я использовала одну из вершин шестиугольника), описываем окружность, не отпуская пальца.

Этот инструмент можно использовать на уроках геометрии, особенно он удобен для построения различных геометрических фигур на листах без клеточек.

1. Создание узоров в тетраксисе. Цветок жизни.

При вырисовывании тетраксиса с помощью циркуля нельзя не заметить появление разных интересных узоров. Один из таких узоров, который сразу бросается в глаза имеет название «Цветок жизни».

Изображение “Цветка Жизни”,  одно из самых древних, его можно встретить на поверхностях (стены, пол, колонны…) древнейших зданий, по всему миру.  Исследователи уже нашли его в Ирландии, Турции, Англии, Израиле, Египте, Китае, Тибете, Греции и Японии — повсюду!  Некоторым сохранившимся изображениям “Цветка Жизни”, например, египетским, более 5000 лет.

Цветок жизни был знаком и Пифагору, возможно, он и послужил основой, для создания тетраксиса…

Не был утрачен “Цветок Жизни” и в более позднее время. Его изображение встречается, например, в черновиках Леонардо да Винчи…

1. Выводы.

Выполнив свою работу по изучению понятия «тетраксис», я узнала много нового и интересного. Я изучила литературу по данной теме, научилась строить эту фигуру различными способами. Больше всего мне понравился способ построения тетраксиса с помощью циркуля и линейки – это очень увлекательный и занимательный процесс. Кроме того, в процессе построения тетраксиса с помощью окружностей вырисовываются красивые узоры, известные человечеству с давних времен. Построив тетраксис, я изучила его геометрические свойства, опираясь на свойство его соседних точек. Оказалось, что в тетраксисе можно построить множество геометрических фигур. Далее я изготовила модель тетраксиса и использовала его в качестве инструмента для построения геометрических фигур. Это оказалось очень удобно, потому что такой инструмент заменяет циркуль, линейку и уголок. Его удобно применять для выполнения несложных построений. Таким образом, цель моей работы была достигнута, поставленные задачи выполнены.

Литература:

Большой энциклопедический словарь

А. М. Воронец “Геометрия циркуля”,1934г

Д. Ефремов “Новая геометрия треугольника”, изд-во Ленанд, 2005

Аргунов Б.И., Балк М.Б. «Геометрические построения на плоскости», издательство «Учпедгиз», 1957 г

Интернет-ресурсы:

https://tetraksis.com/

https://pikabu.ru/story/tsvetok_zhizni_4747003

6

Отдел образования администрации города Енакиево

Муниципальная образовательная организация «Общеобразовательная школа №11 города Енакиево»

Конкурс ученических творческих проектов

«Математика вокруг нас»

Номинация: за страницами учебника

Творческая работа на тему

«ТЕТРАКСИС»

Выполнила:

Ученица 9 класса

Сушко Дарья

Руководитель:

Учитель математики

Икаева Марина Александровна

Енакиево 2018

МОО «Общеобразовательная школа №11 города Енакиево

Конкурс творческих математических проектов

«Математика вокруг нас»

ТЕТРАКСИС

Выполнила

ученица 9 класса

Сушко Дарья Олеговна

Руководитель

учитель математики

Икаева Марина Александровна

Енакиево 2018

ЦЕЛЬ РАБОТЫ:

изучить понятие тетраксис, научиться использовать тетраксис как универсальный инструмент для некоторых геометрических построений.

ЗАДАЧИ:

• изучить литературу по данной теме;
• изучить историю появления и развития понятия «тетраксис»;
• изготовить модель тетраксиса;
• изучить возможности изготовленной модели для геометрических построений .

ТЕТРАКСИС КАК МИСТИЧЕСКИЙ СИМВОЛ

Тетраксис – это треугольная фигура, составленная десятью точками в форме пирамиды. Мистический символ пифагорейцев.

1

Тетраксис символизировал гармонию вселенной, в частности:

• Четыре стихии — земля, воздух, огонь, вода ;
• Базовые понятия геометрии — точка, линия, плоскость, пространство
• Пропорции 4:3 , 3:2 , 2:1, соответствующие музыкальным интервалам октавы, квинты и кварты
• Три космических сферы вокруг Земли — Солнца, Луны и планет

3

2

5

6

4

7

8

9

10

ИЗОБРАЖЕНИЕ ТЕТРАКСИСА ЕСТЬ НА СТЕНЕ АККЕРМАНСКОЙ КРЕПОСТИ В ГОРОДЕ БЕЛГОРОД-ДНЕСТРОВСКИЙ.

ТЕТРАКСИС В ГЕОМЕТРИИ

С точки зрения геометрии тетраксис – это совокупность десяти точек, вписанных в равносторонний треугольник таким образом, что соседние точки равноудалены друг от друга.

ПОСТРОЕНИЕ ТЕТРАКСИСА С ПОМОЩЬЮ ЦИРКУЛЯ И ЛИНЕЙКИ

ПОСТРОЕНИЕ ТЕТРАКСИСА С ПОМОЩЬЮ ЦИРКУЛЯ И ЛИНЕЙКИ

ГЕОМЕТРИЯ ТЕТРАКСИСА

ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРА К ПРЯМОЙ

ПОСТРОЕНИЕ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ

ПОСТРОЕНИЕ РАЗЛИЧНЫХ УГЛОВ В ТЕТРАКСИСЕ

ПОСТРОЕНИЕ РОМБА, ПРЯМОУГОЛЬНИКА И ПАРАЛЛЕЛОГРАММА

В ТЕТРАКСИСЕ

ПОСТРОЕНИЕ ТРАПЕЦИИ И ПРАВИЛЬНОГО ШЕСТИУГОЛЬНИКА В ТЕТРАКСИСЕ

ИЗГОТОВЛЕНИЕ ТЕТРАКСИСА

Тетраксис как геометрический инструмент: вычерчивание окружности с помощью тетраксиса

Тетраксис как геометрический инструмент: вычерчивание некоторых фигур с помощью тетраксиса

Прямоугольник

Параллелограмм

Ромб

Прямоугольный и равносторонний треугольники

Правильный шестиугольник

СОЗДАНИЕ УЗОРОВ В ТЕТРАКСИСЕ. ЦВЕТОК ЖИЗНИ

Изображение “Цветка Жизни”,  одно из самых древних, его можно встретить на поверхностях (стены, пол, колонны…) древнейших зданий, по всему миру.  Исследователи уже нашли его в Ирландии, Турции, Англии, Израиле, Египте, Китае, Тибете, Греции и Японии — повсюду!  Некоторым сохранившимся изображениям “Цветка Жизни”, например, египетским, более 5000 лет.

Выводы:

Выполнив свою работу по изучению понятия «тетраксис», я узнала много нового и интересного. Я изучила литературу по данной теме, научилась строить эту фигуру различными способами. Больше всего мне понравился способ построения тетраксиса с помощью циркуля и линейки – это очень увлекательный и занимательный процесс. Кроме того, в процессе построения тетраксиса с помощью окружностей вырисовываются красивые узоры, известные человечеству с давних времен. Построив тетраксис, я изучила его геометрические свойства, опираясь на свойство его соседних точек. Оказалось, что в тетраксисе можно построить множество геометрических фигур. Далее я изготовила модель тетраксиса и использовала его в качестве инструмента для построения геометрических фигур. Это оказалось очень удобно, потому что такой инструмент заменяет циркуль, линейку и уголок. Его удобно применять для выполнения несложных построений. Таким образом, цель моей работы была достигнута, поставленные задачи выполнены.

Литература:

Большой энциклопедический словарь

А.М.Воронец «Геометрия циркуля», 1934

Д. Д. Ефремов “Новая геометрия треугольника”, изд-во Ленанд, 2005

Аргунов Б.И., Балк М.Б. «Геометрические построения на плоскости», издательство «Учпедгиз», 1957 г

Интернет-ресурсы:

https://tetraksis.com/

https://pikabu.ru/story/tsvetok_zhizni_4747003