Областной конкурс научно – исследовательских работ учащихся
«Детские исследования – великим открытиям»
Муниципальное бюджетное общеобразовательное учреждение
Избердеевская средняя общеобразовательная школа
им. Героя Советского Союза В. Кораблина
Направление: физика
Изучение закона сохранения импульса
Авторы:
Лапшина Александра Андреевна,
ученица 8 класса;
Мухортов Максим Валентинович,
ученик 8 класса
Руководитель:
Уродовских Елена Николаевна,
учитель физики
с. Петровское
2017 г
Содержание
Введение……………………………………………………………….…3
Теоретическая часть……………………………………………………..4
Практическая часть………………………………………………………7
Заключение.....……………………………………………………………11
Список использованной литературы…………………………………...12
Введение
Движение в природе не возникает из ничего и не исчезает – оно передаётся от одного тела к другому. Результат взаимодействия тел зависит и от массы тел и от их скорости одновременно.
Еще великий французский философ, математик, физик и физиолог, основатель новоевропейского рационализма и один из влиятельнейших метафизиков Нового времени Рене Декарт ввел такое понятие как "количество движения". Он же высказал закон сохранения количества движения, дал понятие импульса силы: "Я принимаю, что во Вселенной... есть известное количество движения, которое никогда не увеличивается, не уменьшается, и, таким образом, если одно тело приводит в движение другое, то теряет столько своего движения, сколько его сообщает." Как один из основополагающих законов физики, он дал неоценимое орудие исследования ученым, ставя запрет одним процессам и открывая дорогу другим. Взрыв, реактивное движение, атомные и ядерные превращения — везде работает этот закон. Нам захотелось опытным путем убедиться в справедливости слов Р. Декарта, которые есть и в современных учебниках физики, а называем мы это, несколько измененное со временем утверждение, законом сохранения импульса.
Цель работы: убедиться в справедливости закона сохранения импульса при упругом ударе шаров. Задачи: изучить дополнительный материал по данной теме из различных источников; провести опыты по соблюдению закона сохранения импульса в результате соударения различных тел при абсолютно упругом центральном и нецентральном ударах; провести расчеты и сделать выводы о справедливости закона сохранения импульса.
Объект исследования: система двух соударяющихся тел. Предмет исследования: закон сохранения импульса. Гипотеза: возможно в лабораторных условиях подтвердить закон сохранения импульса.
Теоретическая часть
При изучении кинематики и динамики на уроках и элективном курсе мы познакомились со многими физическими величинами, характеризующими движение тел (координаты, скорость, ускорение), а также с величиной, определяющей изменение скорости тела – силой и импульсом.
Импульсом тела называют вектор, равный произведению массы тела на его скорость движения: 
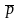 =
=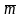
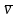
Совокупность взаимодействующих между собой тел образует механическую систему. Для замкнутой системы тел установлен закон сохранения импульса: геометрическая сумма импульсов всех тел, входящих в замкнутую систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
В данной работе применяется закон сохранения импульса к системе двух соударяющихся тел.
Удар тел – кратковременное взаимодействие двух и более тел, возни-кающее в результате их соприкосновения. Величина ударных сил взаи-модействия во много раз превосходит величины всех остальных сил, действующих на тела. Поэтому в процессе удара систему соударяющихся тел можно считать замкнутой и применять к ней закон сохранения импульса.
Абсолютно упругим называется удар, в результате которого механическая энергия не переходит в другие формы энергии. При этом происходит переход кинетической энергии в потенциальную энергию деформации, а также обратный переход. Упругому удару соответствует полное восстановление формы соударяющихся тел. При абсолютно упругом ударе выполняются законы сохранения энергии и импульса.
Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. При этом выполняется только закон сохранения импульса.
Если направление движения двух соударяющихся шаров в момент их соприкосновения совпадает с прямой, соединяющей центры шаров, то удар называется центральным. В данной работе рассматривается случай и нецентрального абсолютно упругого удара.
В справедливости закона сохранения импульса необходимо убедиться на опыте, исследуя столкновения шаров на установке (рис. 1).
 Рис.1.
Рис.1.
Шар, скатившись с лотка, движется по параболе до удара о поверхность стола. Горизонтальные составляющие скорости шара и его импульса во время свободного падения не изменяются, так как нет сил, действующих на этот шар в этом направлении. Затем на краю лотка ставим второй шар и запускаем первый шар точно таким же образом, как и в первом опыте. После соударения в горизонтальном направлении с лотка слетают оба шара. При этом часть импульса движения первого шара передается второму. По закону сохранения векторная импульса сумма импульсов первого р1 и второго р2 шаров до столкновения должна быть равна сумме импульсов этих шаров после столкновения.
Если оба шара после столкновения движутся вдоль одной прямой и в том же направлении, в каком двигался первый шар до столкновения, то от векторной формы записи закона сохранения импульса можно перейти к алгебраической форме: р1 + р2 = р'1 + р'2.
А так как p = mv, то
m1v1+ m2v2 = m1v'1 + m2v'2
Заметим, что скорость второго шара v2 до столкновения равна нулю.
Для проверки выполнения равенства необходимо измерить массы шаров m1 и m2 с помощью весов, а также найти способ узнать скорости шаров v1, v'1, v'2.
Так как во время свободного падения шара по параболе горизонтальная составляющая его скорости не изменяется, она может быть найдена так:
v = ℓ/t , где ℓ - дальность полета шара в горизонтальном направлении, а t - время его свободного падения, равное t = 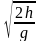 .
.
В последнем уравнении видим, что v и ℓ прямо пропорциональны друг другу, а значит по длине ℓ можно судить о величине горизонтальной скорости. Этим и воспользуемся в данной работе.
Практическая часть
Оборудование: штатив, два шара одинаковой массы и шар большей массы, линейка измерительная, листы белой и копировальной бумаги, лоток, весы.
-
Исследование центрального удара.
-
Используя весы, измерили массы шаров m1 и m2 (рис.2).
 Рис.2
Рис.2
-
Укрепили лоток в лапке штатива таким образом, чтобы горизонтальная часть лотка находилась на высоте 20 см от стола. На столе перед лотком положили лист белой бумаги (рис.1).
-
Взяли шар с большей массой, установили его у верхнего края наклонной части лотка. Сделав несколько пробных пусков, определили с какой высоты надо пускать шар, чтобы место его падения было в районе второй половины листа, но так, чтобы он ни в коем случае не ударялся за пределами листа. Отметили это положение на лотке (рис3).
 Рис.3
Рис.3
На лист белой бумаги положили лист копировальной бумаги.
4. Отпустили шар с края лотка без начальной скорости, чтобы получить отметку падения шара по вертикали.
-
Отпустили шар с намеченной нами отметки на лотке и по отметке на листе белой бумаги и определили его дальность полета в горизонтальном направлении. Опыт повторили 3 раза, нашли среднее значение дальности полета ℓ1.
6. Зная высоту края лотка h над столом, вычислили время падения шара t, затем горизонтальные составляющие его скорости v1 и импульса р1. Все вычисления заносили в таблицу-отчет.
7. Установили на краю горизонтальной части лотка второй шар и проводили запуск первого шара с той же высоты лотка, как в первом опыте. По отметкам на бумаге нашли дальности полетов шаров в горизонтальном направлении после их столкновения. Опыт повторяли три раза, нашли среднее значение дальности полета первого шара ℓ'1 и дальности полета второго шара ℓ'2. По найденным числовым значениям дальностей полетов ℓ'1 и ℓ'2 вычислили числовые значения скоростей шаров после столкновения v'1 и v'2 и их импульсов р'1 и р'2 (табл.1).
8. Сравнили импульс первого шара до столкновения р1 с суммой импульсов двух шаров после столкновения р'1 + р'2.
Табл. 1. Результаты измерений и вычислений.
|
| До удара | После удара |
| Шар № | 1 | 2 | 1 | 2 |
| Масса шара m, (кг) | m1 =0,02475 | m2 =0,00709 | - | - |
| Дальность полета ℓ, (м) | ℓ1=0,25 | ℓ2 =0 | ℓ'1= 0,17 | ℓ'2 =0,23 |
| Высота падения шаров h, (м) | h =0,2 |
| Время полета t, (с) | t = 0,2 |
| Горизонтальная скорость v, (м/с) | v1 =1,25 | v2 =0 | v'1 =0,85 | v'2 =1,15 |
| Импульс р, (кг·м/с) | р1 =0,03094 | р2 =0 | р'1 =0,021 | р'2 =0,00815 |
| Сумма импульсов Σр, (кг·м/с) | Σр = р1 + р2 =0,03094 | Σр' = р'1 + р'2 =0,0292 |
II. Исследование нецентрального удара.
1. Взяли два шара одинаковой массы. Один шар установили на краю лотка так, что вектор скорости первого шара при столкновении был направлен мимо центра второго шара. При таком столкновении, называемом нецентральным, векторы скорости шаров после столкновения v'1 и v'2 имеют различные направления. По закону сохранения импульса должно выполняться векторное равенство:
а так как m1 = m2, то в векторном виде
2. Для проверки последнего равенства получили отметки падения шара по вертикали с края лотка (точка А), точки падения шара после свободного скатывания (точка В) и точек падения шаров после нецентрального столкновения (точки С и D) (рис 4).
Рис. 4. 
3. Соединили точку А с точками В, С и D. Вектор АВ параллелен вектору скорости v1 шара и пропорционален ему по длине. Векторы АС и АD параллельны векторам скорости v'1 и v'2 после их столкновения. При выполнении закона сохранения импульса сумма векторов АD и АС должна быть равна вектору АВ. Построили параллелограмм со сторонами АD и АС и провели его диагональ из вершины А. Сравнили эту диагональ с вектором АВ (рис.5,6)
 Рис.5
Рис.5
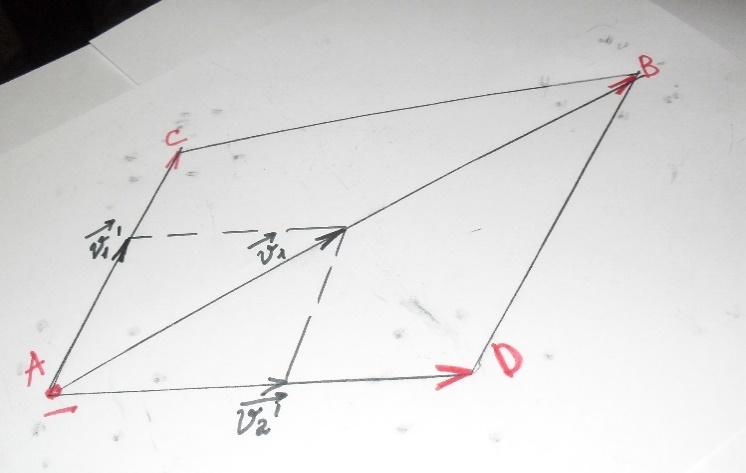 Рис.6
Рис.6
Выводы: убедились на опыте в справедливости закона сохранения импульса: при любых взаимодействиях тел векторная сумма импульсов тел до взаимодействия равна векторной сумме импульсов тел после взаимодействия. Обнаруженные в опыте отклонения от закона сохранения импульса не выходят за пределы границ погрешностей измерений.
Заключение
В результате проведенных опытов и изучения теоретического материала, на основе наблюдений за движением тел до столкновения и после него, можно заметить, что если скорость одного шара уменьшилась, то скорость второго шара увеличилась. В результате механического взаимодействия тел происходит обмен скоростью движения. Скорость каждого из тел меняется во время соударения. То есть скорость не является сохраняющейся мерой механического движения. При взаимодействии тел сохраняется произведение массы на скорость, т.е. импульс системы тел. Справедлив закон сохранения импульса: геометрическая сумма импульсов всех тел, входящих в замкнутую систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Гипотеза подтвердилась. При выполнении работы оказывалась следующая поддержка научным руководителем: помощь в подборе литературы, структурировании материала, предоставлении оборудования для проведения эксперимента. Практическая значимость работы заключается в том, что данный материал можно использовать на уроках физики и занятиях элективного курса.
Список использованной литературы
1. Энциклопедический словарь юного физика/ Сост. В.А. Чуянов. – М.: Педагогика, 1984. – 352 с., ил.
2. Энциклопедия «Физика», Москва, «Аванта +», 2002 г.
3. Сверхзадача. Творческие лабораторные работы. http://sverh-zadacha.ucoz.ru/lab_rab/index.htm
4. Центр онлайн обучения Фоксфорд. Интерактивный учебник по физике https://www.youtube.com/playlist?list=PL66kIi3dt8A6Hd7soGMFXe6E5366Y66So






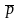 =
=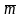
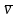
 Рис.1.
Рис.1.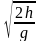 .
.  Рис.2
Рис.2 Рис.3
Рис.3
 Рис.5
Рис.5 Рис.6
Рис.6


















