Содержание
1.
Введение.
2. Теоретическая часть.
2.1. Место, краткое содержание, цели изучения темы.
2.2. Что такое координаты.
2.3. Декартовы координаты на плоскости.
2.4. Формула расстояния между двумя точками.
2.5. Задания для самопроверки.
2.6. Консультация первого уровня.
2.7. Консультация второго уровня.
2.8. Консультация третьего уровня.
3. Векторы на плоскости.
3.1. Понятие вектора.
3.2. Равенство двух векторов.
3.3. Сложение и вычитание векторов.
3.4. Умножение вектора на число.
4. Координаты вектора.
4.1. Теорема о единственности разложения вектора.
4.2. Задания для самопроверки.
4.3. Консультация первого уровня.
4.4. Консультация второго уровня.
4.5. Консультация третьего уровня.
5. Скалярное произведение векторов.
5.1. Определение скалярного произведения.
5.2 Свойства скалярного произведения.
5.3. Скалярное произведение векторов в координатной форме.
6. Исторические сведения.
7. За страницами учебника математики.
8. Приложения.
8.1. Подготовительный вариант контрольной работы.
8.2. Контрольная работа по теме "Векторы. Метод координат".
8.3 Задачи военной направленности.
9. Список литературы.
Введение
Учебный кейс по теме «Векторы. Метод координат» рекомендован преподавателям и кадетами на практических занятиях, в часы самоподготовки, дополнительных и индивидуальных консультаций.
Содержание кейса соответствует рабочей программе курса математики Омского кадетского военного корпуса.
Кратко изложены основные теоретические сведения по теме: «Векторы. Метод координат», рассмотрены примеры решения типовых задач, приведены задания к контрольной работе, дан список рекомендуемой литературы
Учебный кейс поможет преподавателям математики ОД «Математика, информатика и ИКТ» в подготовке к урокам, для обучения, закрепления и контроля усвоения теоретических знаний и отработки практических умений кадетов, а также для развития навыков самостоятельной работы и самоконтроля. В кейсе кратко изложены теоретические сведения по теме «Векторы. Метод координат на плоскости», рассмотрены примеры решения типовых задач, даны консультации первого, второго и третьего уровней, приведены индивидуальные задания, включающие задачи военно-прикладного характера.
Задания составлены таким образом, что кадеты могут выполнять задания постепенно, по мере изучения темы. При этом у обучающихся складывается наиболее полное представление о тех основных умениях, которые потребуются от них после изучения темы. Важным является наличие совместных заданий на геометрическую и алгебраическую интерпретацию понятия вектора.
Чтобы успешно выполнить задания контрольной работы, рекомендуем решить “Задания для самопроверки”. Не отчаивайтесь, если вы не знаете, как решать эти задачи. В нашем кейсе предусмотрены консультации трех уровней:
Консультация первого уровня – небольшая подсказка, которая натолкнет вас на правильную мысль.
Консультация второго уровня – более серьёзная подсказка, которая предлагает конкретное, но не окончательное решение, постарайтесь завершить его самостоятельно.
Консультация третьего уровня – окончательное решение задачи. Вдумчиво и внимательно разберите это решение. Не отчаивайтесь, что не смогли самостоятельно решить задачу. Постарайтесь понять предложенное решение и аналогичная задача вам покорится.
Кто не знает,
в какую гавань он плывет,
для того нет попутного ветра.
Сенека
Теоретическая часть
Место, краткое содержание, цели изучения темы.
Тема № 2 «Векторы. Метод координат», на которую отводится 18 часов, изучается в 9 классе, в I четверти.
Основные подтемы:
- Векторы. Действия над векторами (7 часов);
- Метод координат (11 часов).
Изучение темы «Векторы. Действия над векторами» в курсе геометрии преследует две цели: подготовить кадетов к восприятию действий над векторными величинами в физике и показать, как можно использовать векторы при решении геометрических задач. Особое внимание следует уделить умению выполнять действия над векторами и демонстрации возможностей векторного метода в геометрии.
Тема «Метод координат» служит основой аналитической геометрии, в которой геометрические фигуры изучаются с помощью методов алгебры.
2.2. Что такое координаты.
В повседневной речи вы могли слышать такую фразу: «Оставьте мне ваши координаты».
Что означает это выражение?
Как ответить на эту просьбу?
Действительно, это выражение означает, что собеседник должен оставить свой адрес или номер телефона, которые и считаются в этом случае координатами человека. Главное здесь в том, что по этим данным человека можно найти. Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило, по которому определяется положение того или иного объекта.
Системы координат пронизывают всю практическую жизнь человека. Кроме почтовых адресов и номеров телефонов, вы знакомы с системой координат в зрительном зале кинотеатра (номер ряда и номер места), в поезде (номер вагона и номер места), с системой географических координат (долгота и широта) и т.п.
Те из вас, кто играл в «морской бой», пользовались при этом соответствующей системой координат (рис.1). Аналогичная система координат используется в шахматах, только горизонтали на шахматной доске всегда обозначаются латинскими буквами (рис.2).

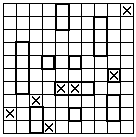
Рис. 1 Рис.2
Такого рода «клетчатые» координаты обычно используются на военных, морских, геологических картах («в квадрате 80-36 обнаружена неизвестная подводная лодка»). Применяются они и на туристических схемах городов для облегчения поиска нужной улицы или какой-либо достопримечательности. Термин «координаты» произошел от латинского слова ordinatus – «упорядоченный», а приставка «со» указывает на «совместность»: координат обычно бывает две или более.
Вы умеете задавать координаты на прямой. Для этого на прямой выбираем начало отсчета, положительное направление и единичный отрезок. После этого любая точка прямой получает свою собственную координату. Например, точки А, В, С имеют координаты, соответственно –1,5; 2,5; 4 (рис.3).
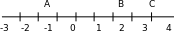
· · А (-1,5); В (2,5); С (4)
Рис.3
Координата точки указывает, таким образом, ее место на координатной прямой. Но как же тогда указать положение точки на плоскости?
Декартовы координаты на плоскости.
Рассмотрим две взаимно – перпендикулярные прямые на плоскости. Обозначим через О точку пересечения этих прямых и будем считать, что каждая из них является числовой осью или осью координат с началом в точке О и равными единичными отрезками. При этом одну из этих прямых будем считать первой и назовем осью ОХ или осью абсцисс, а вторую прямую – осью ОУ или осью ординат ( рис. 4). Такая пара перпендикулярных прямых задает на плоскости декартову систему координат. Теперь по достаточно простому правилу каждой точке плоскости можно поставить в соответствие пару чисел, а вернее, упорядоченную пару чисел – координаты этой точки. Пусть А – произвольная точка плоскости, тогда первая координата точки А, или абсцисса точки А (будем обозначать ее буквой х), является положительной, если А1 лежит на положительной полуоси ОХ, и отрицательной в противоположном случае (рис.4,5).
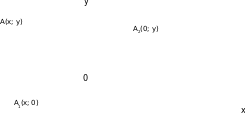
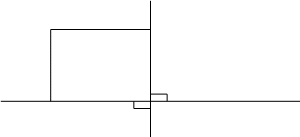



Рис.4 Рис.5
Тот факт, что х и у являются соответственно абсциссой и ординатой точки А, будем записывать следующим образом: А (х; у). Очевидно, что точке О соответствуют две нулевые координаты: О (0; 0).
Введя таким образом координаты на плоскости, мы установим взаимно однозначное соответствие между точками плоскости и упорядоченными парами чисел. Выражение «взаимно однозначное соответствие» в данном случае означает, что каждой точке плоскости соответствует пара чисел, а каждой паре чисел – точка плоскости. При этом важно, в каком порядке записаны эти числа. Например М (2; 3) и К (3; 2) - различные точки плоскости (рис.6).
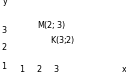

Рис.6
Именно этот факт обозначает прилагательное «упорядоченная». Для всех точек оси абсцисс ордината равна нулю, а для точек оси ординат нулю равна абсцисса.
2.4. Формула расстояния между двумя точками.
Пусть А и В – две точки плоскости, координаты которых в декартовой системе координат таковы: А (х1;у1), В (х2;у2), тогда
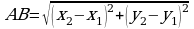
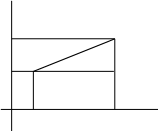
Эта формула, по существу, является теоремой Пифагора, записанной в координатной форме. В самом деле, пусть точки А1 и В1 соответственно проекции точек А и В на ось абсцисс, точка М – проекция точки А на прямую ВВ1 (рис.8).
 у
у
В
B2(0;y2)
A2(0;y1) А |x2-x1| M
0 A1(x1;0) B1(x2;0) x
Рис.8
Итак, АВ – гипотенуза прямоугольного ∆ АВМ, но
АМ = А1В1 = │ х2 – х1 │
ВМ = А2В2 = │ у2 – у1 │
Следовательно, АВ2 = АМ2 + ВМ2 = (х2 – х1 )2 + (у2 – у1 )2 и формула доказана.
2.5. Задания для самопроверки.
Задача 1.
На координатной плоскости отметьте точки А(-2; -7), В(-2; 7), С(2; 7). Постройте четвертую точку D так, чтобы получился прямоугольник АВСD, вычислите его периметр и площадь.
Задача 2.
Найдите все точки оси абсцисс, удаленные на расстояние, равное 5, от точки М (14; 3).
Задача 3.
Высота треугольника, равная 10 см, делит основание на два отрезка, равные 10 см и 4 см Найдите медиану, проведенную к меньшей из двух других сторон.
Если вы решили эти задачи, то проверьте свой ответ на стр.19.
Если вы не знаете, как решать – обращайтесь к консультации первого уровня, т. е. к небольшой подсказке на с. 6.
2.6. Консультация первого уровня.
Задача 1.
Точка D расположена симметрично точке А относительно оси ОУ.
Найти длину отрезков АВ и ВС.
Задача 2
Построить равнобедренный Δ KML, одна из вершин которого М (14; 3), а две другие
K и L лежат на оси ОХ.
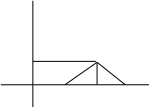
Задача 3.
Расположите Δ ABC в прямоугольной системе координат так, чтобы высота BO данного треугольника лежала на оси ОУ, а основание AC на оси ОХ.
2

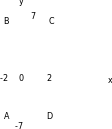


 .7. Консультация второго уровня.
.7. Консультация второго уровня.
Задача 1.
D (2; -7), т.к. А (-2; -7); В(-2; 7), то
длина АВ равна
АВ = 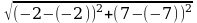 ,
,
АВ = 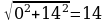 .
.
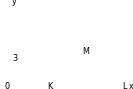
Задача 2
М (14; 3);
К (х1; 0);
L (х2; 0);
|КМ| = 5;
|LМ| = 5;
См. §3 настоящего пособия на с. 5.


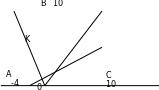
Задача 3 Δ АВС, А (-4; 0), В (0; 10), С (10; 0)
АС = 14; ВС = 10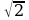 – по теореме Пифагора в
– по теореме Пифагора в
Δ ВОС. Кроме того, АООС, следовательно АВ как гипотенузы двух треугольников с общим катетом ВО, таким образом АВ – наименьшая сторона. Пусть СК – медиана Δ АВС, см [1] п.89, с.225.
2.8. Консультация третьего уровня.
Задача 1.
Так как В (-2; 7), С (2; 7), следовательно 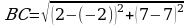 ,
,
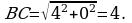
РАВСD = (4+14) 2 = 56 (линейных единиц),
SАВСD = 4 14 = 56 (квадратных единиц).
Задача 2.
Длина отрезка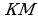 =
= 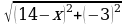 ;
;
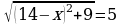 ;
;
(14-х)2+9 = 25;
196 – 28х + х2 + 9 = 25;
х2 – 28х + 180 = 0;
х1,2=14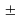
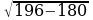 ; х1,2=14
; х1,2=14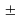 4;
4;
х1 = 10; х2 = 18.
Следовательно, К(10; 0), L(18; 0).
Задача 3
Найдем координаты точки К (х ; у), так как А (-4; 0), В (0; 10) и К середина отрезка АВ, то
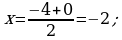
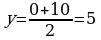 ,
,
то есть координаты точки К (-2; 5).
Найдем длину отрезка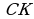 , т.к. С(10;0), то
, т.к. С(10;0), то
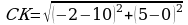 ;
;
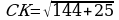 =
=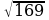 =13,
=13,
то есть длина медианы, проведенной к меньшей стороне равна 13 см.
Векторы на плоскости.
Понятие вектора.
Рассмотрим на плоскости две точки А и В. Обозначим через 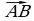 вектор АВ, понимая под этим направленный отрезок АВ, то есть отрезок, у которого точка А является началом, а точка В – концом (рис.9).
вектор АВ, понимая под этим направленный отрезок АВ, то есть отрезок, у которого точка А является началом, а точка В – концом (рис.9).
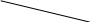 конец вектора
конец вектора
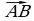
начало вектора
рис. 9
Таким образом, точки А и В, ограничивающие вектор 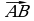 , играют различную роль. Именно в этом состоит главное различие между вектором
, играют различную роль. Именно в этом состоит главное различие между вектором 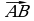 и отрезком АВ. Вектор характеризуется направлением и длиной.
и отрезком АВ. Вектор характеризуется направлением и длиной.
Направление – множество сонаправленных лучей.
Длина вектора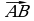 – расстояние от начала вектора до его конца (то есть длина отрезка АВ).
– расстояние от начала вектора до его конца (то есть длина отрезка АВ).
Длина (модуль) вектора 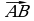 обозначается
обозначается 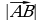 .
.
Две точки А и В плоскости задают два различных вектора 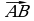 и
и 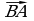 одинаковой длины и противоположного направления.
одинаковой длины и противоположного направления.
Примеры векторов: сила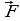 , скорость
, скорость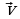 , перемещение
, перемещение 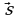 , ускорение
, ускорение  .
.
Равенство двух векторов.
Два вектора 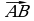 и
и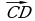 , расположенные на одной прямой, считаются равными, если равны отрезки АВ и CD, то есть равны длины этих векторов, а лучи АВ и CD задают одинаковые направления. Если же векторы
, расположенные на одной прямой, считаются равными, если равны отрезки АВ и CD, то есть равны длины этих векторов, а лучи АВ и CD задают одинаковые направления. Если же векторы 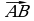 и
и 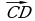 не расположены на одной прямой, то они считаются равными, если четырехугольник АВDC (вершины рассматриваются в данном порядке) является параллелограммом (рис.10).
не расположены на одной прямой, то они считаются равными, если четырехугольник АВDC (вершины рассматриваются в данном порядке) является параллелограммом (рис.10).
Таким образом, мы можем вектор не только перемещать вдоль соответствующей прямой, но и переносить его начало в любую точку плоскости. Следовательно, для обозначения вектора нет необходимости указывать его начало и конец. Можно использовать обозначения вида  ,
,  ,
, 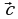 и т.п., помещая в случае необходимости начало соответствующего вектора в любую точку плоскости. Для длины вектора
и т.п., помещая в случае необходимости начало соответствующего вектора в любую точку плоскости. Для длины вектора  будем использовать обозначение |
будем использовать обозначение | |, читая «длина вектора
|, читая «длина вектора  » или «модуль вектора
» или «модуль вектора  » (рис. 11).
» (рис. 11).
D




A
B
C
D



C
B


A
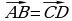
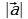 – модуль вектора
– модуль вектора .
.
рис. 10 рис.11
Нулевым называется вектор, длина которого равна нулю (его начало и конец совпадают). Обозначается нулевой вектор 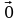 .
.
Если два вектора  и
и  можно расположить на параллельных прямых или вдоль одной прямой, то эти векторы будем называть коллинеарными.
можно расположить на параллельных прямых или вдоль одной прямой, то эти векторы будем называть коллинеарными.
Нулевой вектор мы считаем коллинеарным любому вектору.
Сложение и вычитание векторов.
Суммой двух векторов АВ=а и ВС=b будем называть вектор АС=c, полученный по следующему правилу треугольника:
р
 асположим векторы
асположим векторы и
и  так, чтобы начало вектора
так, чтобы начало вектора  совпадало с концом вектора
совпадало с концом вектора  (рис.12), тогда началом вектора
(рис.12), тогда началом вектора 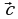 будет начало вектора
будет начало вектора , а его концом – конец вектора
, а его концом – конец вектора 
Рис.12.
Из определения сложения следует, что для любых точек А,В,С имеет место равенство
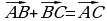
Правило сложения двух неколлинеарных векторов можно сформулировать иначе, в виде правила параллелограмма:
пусть начала векторов  и
и  совпадают; рассмотрим параллелограмм, у которого эти векторы являются смежными сторонами; тогда суммой векторов
совпадают; рассмотрим параллелограмм, у которого эти векторы являются смежными сторонами; тогда суммой векторов  и
и  является вектор
является вектор 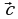 – диагональ этого параллелограмма, с началом в общей для векторов
– диагональ этого параллелограмма, с началом в общей для векторов и
и  точке (рис.13)
точке (рис.13)



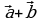

рис. 13
Понятно, что из определения суммы векторов следует равенство
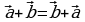
Разностью 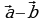 векторов
векторов  и
и  называется вектор
называется вектор 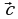 такой, что
такой, что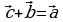 , т.е. это вектор, идущий из конца вектора
, т.е. это вектор, идущий из конца вектора  в конец вектора
в конец вектора  , если векторы
, если векторы  и
и  приведены к общему началу (рис. 14а).
приведены к общему началу (рис. 14а).




 -
- -
-

 -
-

рис. 14а рис. 14б
Разность векторов  и
и  можно построить и другим способом, а именно вычесть из вектора
можно построить и другим способом, а именно вычесть из вектора  вектор
вектор  – это значит (рис. 14б) прибавить к вектору
– это значит (рис. 14б) прибавить к вектору  вектор, противоположный
вектор, противоположный , то есть
, то есть
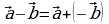
Умножение вектора на число.
Для любого вектора  и любого числа k определяем вектор
и любого числа k определяем вектор 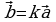 , являющийся произведением вектора
, являющийся произведением вектора  на число k, с помощью следующего простого правила:
на число k, с помощью следующего простого правила:
вектор  коллинеарен вектору
коллинеарен вектору  , причем его направление совпадает с направлением
, причем его направление совпадает с направлением  , если k0, и противоположно, если k
, если k0, и противоположно, если k 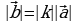 .
.
П
 онятно, что, если k=0, то получаем нулевой вектор, т.е. точку. Таким образом, длина вектора
онятно, что, если k=0, то получаем нулевой вектор, т.е. точку. Таким образом, длина вектора  в k раз больше длины вектора
в k раз больше длины вектора  . Если
. Если 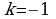 , то получаем вектор –
, то получаем вектор – , равный по длине вектору
, равный по длине вектору  , но противоположно направленный (рис. 15). В частности, это означает, что
, но противоположно направленный (рис. 15). В частности, это означает, что 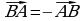 -
-
 -2
-2
2
рис.15
Координаты вектора.
Пусть А и В – две точки координатной плоскости. Их координаты соответственно равны (х1; у1) и (х2; у2).
Тогда координаты вектора 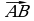 таковы: {х2-х1; у2-у1}. Они получаются вычитанием из координат конца вектора координат начала (рис.16).
таковы: {х2-х1; у2-у1}. Они получаются вычитанием из координат конца вектора координат начала (рис.16).
 y
y
B(x2;y2)
 {x;y} x = x2-x1;
{x;y} x = x2-x1;
A(x1;y1) y = y2-y1;
0 x 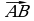 {x; y}.
{x; y}.
рис.16
Понятно, что в какой бы точке плоскости мы ни поместили начало вектора, его координаты будут одними и теми же. При умножении вектора на число его координаты соответственно умножаются на это число, т.е. если вектор  имел координаты {х; у}, то координатами вектора
имел координаты {х; у}, то координатами вектора 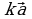 будут {kх; kу}. При сложении (вычитании) векторов их соответствующие координаты складываются (вычитаются), т.е. если векторы
будут {kх; kу}. При сложении (вычитании) векторов их соответствующие координаты складываются (вычитаются), т.е. если векторы  и
и  имели координаты {х1; у1} и {х2; у2}, то координатами вектора
имели координаты {х1; у1} и {х2; у2}, то координатами вектора 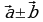 являются
являются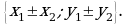
4.1. Теорема о единственности разложения вектора по двум неколлинеарным векторам.


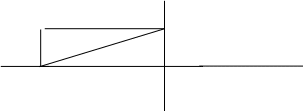 Теорема: Пусть
Теорема: Пусть 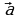 и
и  – два неколлинеарных вектора плоскости. Тогда для любого вектора
– два неколлинеарных вектора плоскости. Тогда для любого вектора 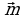 плоскости существует, и притом единственная, пара чисел х и у такая, что
плоскости существует, и притом единственная, пара чисел х и у такая, что 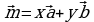 (рис. 17).
(рис. 17).

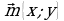
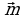 = -3
= -3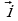 + 2
+ 2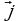 .
.
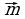
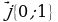
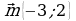
 0
0
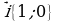

Рис. 17 Рис. 18
Замечание: Рассмотрим декартову систему координат. Обозначим через 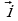 и
и 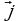 единичные векторы, направленные по осям координат. Представим вектор
единичные векторы, направленные по осям координат. Представим вектор 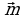 в виде
в виде 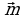 = х
= х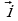 + у
+ у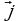 . Коэффициенты х и у в данном случае являются координатами вектора
. Коэффициенты х и у в данном случае являются координатами вектора 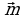 в этой системе координат (рис. 18).
в этой системе координат (рис. 18).
4.2. Задания для самопроверки.
Задача 4.
На координатной плоскости заданы точки А(-1;3), В(2;-5), С(3; 4). Найдите координаты следующих векторов: 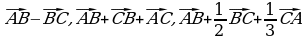 .
.
Задача 5.
Дан квадрат. Докажите, что сумма четырех векторов с началом в центре этого квадрата и с концами в его вершинах равна нулю.
Задача 6.
Найдите координаты четвертой вершины параллелограмма по заданным координатам трех его вершин: А(-5;1), В(-4;4), С(-1; 5). Сколько решений имеет задача?
4.3. Консультация первого уровня.
Задача 4.
Каждая координата вектора равна разности соответствующих координат его конца и начала, т.е., если точки А и В имеют координаты соответственно А (х1; у1), В (х2; у2), то вектор 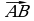 имеет координаты { х2- х1; у2 - у1}.
имеет координаты { х2- х1; у2 - у1}.
Более подробно см. [1] с. 223-225.
Задача 5
См. пункты 4.2, 4.4 данного пособия, на рисунке 10 векторы 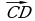 и
и 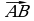 – равные, см. рис.13.
– равные, см. рис.13.
Задача 6.
См. в нашем пособии рис. 13, 16.
4.4. Консультация второго уровня.
Задача 4.
Пусть вектор 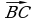 имеет координаты
имеет координаты 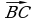 {х; у}, т.к. В (2;-5), С(3;4) , то х=3-2=1;
{х; у}, т.к. В (2;-5), С(3;4) , то х=3-2=1;
у=4-(-5)=4+5=9.
Следовательно, 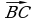 {1; 9}. Тогда
{1; 9}. Тогда 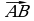 или
или 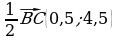 .
.
Задача 5
 В С
В С
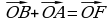
F О 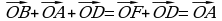
А D
Задача 6
 y Рассмотрим случаи:
y Рассмотрим случаи:
а). АС – диагональ
б). АВ – диагональ
С в). ВС – диагональ
В данного параллелограмма.
А
0 x
4.5. Консультация третьего уровня.
Задача 4.
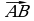 {3; -8},
{3; -8}, 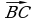 {1; 9}
{1; 9}
Координаты вектора 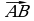 –
– 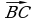 =
= 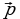 ,
, 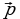 {3-1; -8-9},
{3-1; -8-9}, 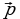 {2; -17}
{2; -17}
Ответ: {2; -17}, {6; -16}, 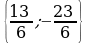
Задача 5
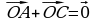 , т.к. эти вектора равны по длине и противоположно направлены.
, т.к. эти вектора равны по длине и противоположно направлены.
Задача 6
а). АС – диагональ параллелограмма ABCD1,
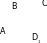
 y тогда
y тогда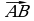 =
=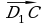 , где D1(х; у)
, где D1(х; у) 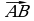 {1;3}
{1;3} 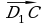 {-1-х; 5-у}
{-1-х; 5-у}
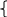

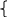 -1-х=1, х=-2,
-1-х=1, х=-2,
5-у=3; у=2; т. е. D1(-2; 2)
б). 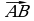 – диагональ параллелограмма ABCD2, сделайте
– диагональ параллелограмма ABCD2, сделайте
рисунок самостоятельно, тогда 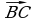 =
=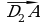 , где D2(х; у)
, где D2(х; у)
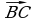 {3;1};
{3;1}; 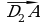 {-5-х; 1-у}
{-5-х; 1-у}
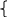

 x -5-х=3, х=-8,
x -5-х=3, х=-8,
1-у=1; у=0; т. е.D2(-8; 0).
в).Аналогично, находим координаты D3, при условии, что ВС – диагональ параллелограмма ABCD3.
D3 (0; 8).
Ответ: (-2; 2), (-8; 0), (0; 8).
5. Скалярное произведение векторов.
Два действия над векторами – умножение вектора на число и сложение (вычитание), с которыми вы познакомились в предыдущем параграфе, в результате вновь дают вектор. Сейчас мы расскажем еще об одной операции, ставящей в соответствие любым двум векторам число. Речь пойдет о скалярном произведении. Скалярной называют величину, задаваемую, в отличие от вектора, одним числом. Слова скаляр и шкала родственны по происхождению (scolaris (лат.) – ступенчатый ).
5.1. Определение скалярного произведения.
Б
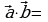
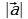
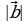 cos φ,
cos φ,
удем через
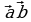
обозначать скалярное произведение ненулевых векторов

и

и определим его равенством
где φ – угол между векторами  и
и  (рис. 18).
(рис. 18).



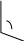



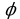
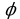
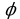 = 0
= 0


Рис. 18

Скалярное произведение двух перпендикулярных векторов равно нулю, так как
Cos 900 = 0. И, наоборот, из равенств
 =0 следует перпендикулярность векторов
=0 следует перпендикулярность векторов  и
и  .
.
Нулевой вектор считается перпендикулярным любому другому вектору. Произведение вектора самого на себя есть скалярный квадрат вектора:
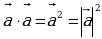
5.2 Свойства скалярного произведения.
Для любых  ,
, ,
,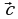 и любого числа
и любого числа 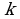 справедливы соотношения:
справедливы соотношения:
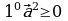 , причем
, причем 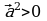 при
при 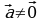
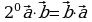 (переместительный закон)
(переместительный закон)
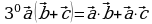 (распределительный закон)
(распределительный закон)
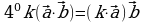 ( сочетательный закон)
( сочетательный закон)
Из свойств скалярного произведения следует, что при умножении векторов можно использовать те же правила, что и при умножении числовых выражений
5.3 Скалярное произведение в координатной форме.
Обозначим через 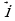 и
и 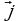 единичные векторы, оси абсцисс и оси ординат соответственно. Эти векторы перпендикулярны, поэтому
единичные векторы, оси абсцисс и оси ординат соответственно. Эти векторы перпендикулярны, поэтому 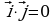 .
.
Пусть в декартовой системе координат векторы  и
и  имеют координаты соответственно {х1; у1} и {х2; у2}(рис. 19), следовательно,
имеют координаты соответственно {х1; у1} и {х2; у2}(рис. 19), следовательно, 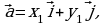
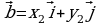
Учитывая эти равенства, а также свойства скалярного произведения, получим
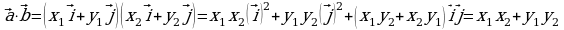 , так как
, так как 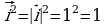 ,
, 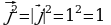 и
и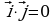 , т.к.
, т.к. 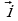 ^
^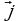 .
.
Таким образом получаем,
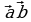 = х1х2 + у1 у2
= х1х2 + у1 у2
у
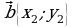
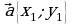
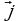
0 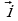 x
x
рис. 19
Замечание: Если некоторый вектор 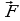 представляет постоянную силу, точка приложения которой перемещается из начала в конец вектора
представляет постоянную силу, точка приложения которой перемещается из начала в конец вектора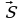 , то работа А этой силы определяется равенством:
, то работа А этой силы определяется равенством:
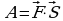
– механический смысл скалярного произведения.
Пример. Вычислите работу, производимую силой 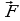 {2; -1}, когда точка ее приложения, двигаясь прямолинейно, перемещается из положения М (1; -2) в положение N (5; -5).
{2; -1}, когда точка ее приложения, двигаясь прямолинейно, перемещается из положения М (1; -2) в положение N (5; -5).
Решение. 1). Найдем координаты вектора 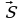 =
= 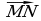 :
: 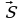 {5-1; -5-(-2)},
{5-1; -5-(-2)}, 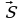 {4; -3}
{4; -3}
2). 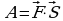 ; А = 2·4 + (-1) (-3) = 8 + 3 = 11 (ед. работы).
; А = 2·4 + (-1) (-3) = 8 + 3 = 11 (ед. работы).
6. Исторические сведения.
Идея координат зародилась в древности. Первоначальное их применение связано с географией и астрономией, с потребностью определять положение светил на небе и пунктов на поверхности земли, при составлении календаря, звездных и географических карт.
Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) обнаружены на стене одной из погребальных камер Древнего Египта. Прямоугольной сеткой пользовались и художники Возрождения.
Более чем за 100 лет до н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести, теперь хорошо известные, географические координаты: широту и долготу и обозначить их числами.
В XIV веке французский математик Н.Оресм ввёл, по аналогии с географическими, координаты на плоскости. Он предложил покрыть плоскость прямоугольной сеткой и назвать широтой и долготой то,что мы теперь называем абсциссой и ординатой.
Это нововведение оказалось чрезвычайно продуктивным. На его основе возник метод координат, связавший геометрию с алгеброй. Точка плоскости – геометрический объект – заменяется парой чисел (х; у), т. е. алгебраическим объектом.
Общематематическое значение метода координат открыли и впервые выявили французские математики XVII века Пьер Ферма и Рене Декарт. Изложение метода координат было впервые опубликовано в “Геометрии” Декарта в 1637г. Отсюда и названия: “Декартова система координат”, “Декартовы координаты”.
Термины «абсцисса», от латинского abscissus – отсекаемый (отрезок на оси иксов), «ордината» от латинского ordinatus – упорядоченный (отрезок на оси игреков) восходят к латинскому переводу (XVI век) сочинений великого древнегреческого математика Аполлония и были введены в употребление в 1670-1680гг. Г.В. Лейбницем. Им же абсцисса вместе с ординатой были названы координатами.
Трудно переоценить значение декартовой системы координат в развитии математики и её приложений. Огромное количество задач, требовавших для решения геометрической интуиции, специфических методов, получило решение, состоящие в аккуратном проведении алгебраических выкладок.
Кривые и поверхности, определяемые ранее геометрически, получили описание в виде формул. Более того, рассматривая различные уравнения и изображая соответствующие линии и поверхности, математики, получили новые геометрические образы, оказавшиеся очень полезными в приложениях.
7. За страницами учебника математики.
Наряду с декартовой прямоугольной системой координат употребляются и другие системы координат на плоскости. Например, декартова косоугольная система координат.
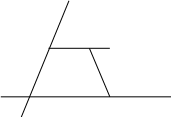
y
M(X0;Y0)
M (x0;y0)
y0
0 x0 xx
Как определяются координаты точки в такой системе координат, ясно из рисунка; в некоторых случаях оказывается необходимым брать по осям координат разные единицы масштаба.
Есть координаты, более существенным образом отличающиеся от декартовых, например полярные координаты. Полярные координаты точки на плоскости определяются следующим образом. На плоскости берётся числовая ось (смотри рисунок).
 φ =
φ =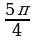 М(ρ; φ)
М(ρ; φ)
 М(3;
М(3; 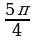 )
)
M
Начало координат этой оси (точка О) называется полюсом, а сама ось – полярной осью. Для определения положения точки М достаточно указать два числа: ρ – полярный радиус (расстояние от полюса до этой точки) и φ – полярный угол (угол поворота от полярной оси до луча ОМ). На рисунке полярный радиус ρ равен 3, а полярный угол φ равен 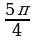 . Таким образом, каждой точке М плоскости сопоставляется пара чисел (ρ, φ). Но если в декартовой системе координат эта пара определяется однозначно, то в полярной системе число φ определено уже неоднозначно: парам чисел (ρ; φ+2 πn) соответствует одна и та же точка при любом целом n. Направление полярной оси можно выбирать произвольно. Так, географы предпочитают направление полярной оси на север и соответствующий полярный угол называют азимутом, а артиллеристы отсчитывают азимут от направления на юг.
. Таким образом, каждой точке М плоскости сопоставляется пара чисел (ρ, φ). Но если в декартовой системе координат эта пара определяется однозначно, то в полярной системе число φ определено уже неоднозначно: парам чисел (ρ; φ+2 πn) соответствует одна и та же точка при любом целом n. Направление полярной оси можно выбирать произвольно. Так, географы предпочитают направление полярной оси на север и соответствующий полярный угол называют азимутом, а артиллеристы отсчитывают азимут от направления на юг.
8. Приложения.
8.1. Подготовительный вариант контрольной работы.
| Дано | Найти, построить | Формула, правило | Образец решения |
Координаты точек А (х1; у1), В (х2; y2) | Координаты вектора  = = 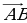
| А (х1; у1), В (х2;У2) 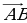 {х1-х2; у1-у2} {х1-х2; у1-у2}
| А(0; 0), В(1; 1), 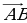 {1-0; 1-0}, {1-0; 1-0}, 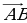 {1; 1} {1; 1} А(-3; -3), В(2; -7), 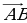 {2-(-3); -7-(-3)}, {2-(-3); -7-(-3)}, 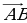 {5; -3} {5; -3} А (6; 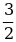 ), В (3; 1), ), В (3; 1), 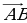 {3-6; 1- {3-6; 1-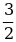 }, }, 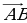 {-3; {-3; 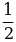 } } |
Вектор  {х; у} {х; у}
| Длину вектора  (абсолютную величину или модуль вектора | |). |). |  {х2; у2} {х2; у2}
|  {4; -3}, {4; -3},  {-2; -2} {-2; -2} | | = | = 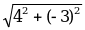 = = 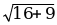 = = 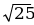 = 5 = 5 | | = | = 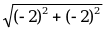 = = 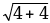 = = 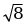 = 2 = 2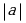 |
Векторы  (х1; у1), (х1; у1),
 (х2; y2) (х2; y2)
| Построить на координатной сетке  , ,  , ,  + +  . .
| Векторы  , ,  строим как радиус-векторы. строим как радиус-векторы. Вектор ( + +  ) строим по правилу параллелограмма ) строим по правилу параллелограмма |  {4; -3} {4; -3}  {-2; -2} {-2; -2}
|
Векторы  (х1; у1), (х1; у1),
 (х2; y2) (х2; y2)
| Найти координаты вектора  + +  и его абсолютную величину. и его абсолютную величину. |  + +  = = 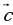 , , 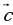 {x; y} {x; y}
x = х1+х2, y = у1+у2 |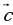 | = | = 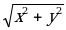 |  {4; -3}, {4; -3},  {-2; -2} {-2; -2}  + +  = = 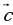 , , 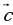 {4+(-2); (-3) + (-2)}, {4+(-2); (-3) + (-2)}, 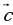 {2; -5} {2; -5} |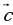 | = | = 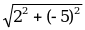 = = 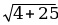 = = 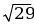 |
Векторы  (х1; у1), (х1; у1),
 (х2; у2) (х2; у2)
| Построить на координатной сетке  , ,  , ,  - -  . . | Векторы  , ,  строим как радиус-векторы. строим как радиус-векторы. Вектор  – –  строим как вектор строим как вектор  + (- + (- ) по правилу треугольника ) по правилу треугольника |  {4; -3} {4; -3}  {-2; -2} {-2; -2}
|
| Дано | Найти, построить | Формула, правило | Образец решения |
Векторы  (х1; у1), (х1; у1),
 (х2; y2) (х2; y2)
| Найти координаты вектора  , , 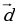 = m = m + n + n
|  {х1; у1} {х1; у1}
m {mх1; mу1} {mх1; mу1} | 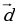 = 3 = 3 – – 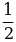  ; ;  {4; -3}, {4; -3},  {-2; -2}, 3 {-2; -2}, 3 {12; -9}, {12; -9},  , , 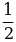  {-1; -1} {-1; -1} 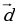 {12-(-1);-9-( -1)}; {12-(-1);-9-( -1)}; 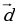 {13; -8} {13; -8}
|
Векторы  (х1; у1), (х1; у1),
 (х2; y2) (х2; y2)
| Скалярное произведение  × × 
|  × ×  = х1х2 + у1 у2 = х1х2 + у1 у2
|  {4; -3}, {4; -3},  {-2; -2} {-2; -2}  × ×  = 4× (-2) + (-3) × (-2) = -8 + 6 = -2 = 4× (-2) + (-3) × (-2) = -8 + 6 = -2
|
Скалярное произведение  × ×  , ,  =АВ =АВ А(х1; у1), В(х2; y2) ( ^ ^ ) = φ ) = φ | Найти модуль вектора  |  × ×  = | = | | × | | × | | cos φ, | cos φ, | | = | | = |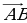 |= |= √ (х2 – х1 )2 + (у2 – у1 )2 |  × ×  = 20 = 20 А(0; -5), В(3; -1),  ↑↑ ↑↑ | | = | | = |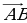 |= |= 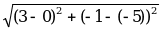 = = 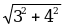 = = 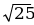 = 5 = 5 Т.к.  ↑↑ ↑↑ , то Ðφ = 0, , то Ðφ = 0, | | = | = 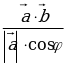 = = 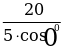 = = 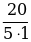 = 4 = 4 |
Координаты точек А(х1; у1), В(х2; y2), С(х3;у3). | Найти угол между векторами 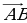 и и 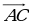 | 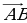 {х2 – х1 ; у2 – у1 } {х2 – х1 ; у2 – у1 } 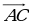 {х3 – х1 ; у3 – у1 } {х3 – х1 ; у3 – у1 }
сosφ = 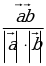 | А(1;3) В(4; 7) С(-4; 15) 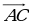 {4– 1; 7 – 3 } {4– 1; 7 – 3 } 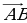 {3 ; 4 } {3 ; 4 } 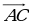 {-4– 1; 15 – 3 } {-4– 1; 15 – 3 } 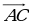 {-5 ; 12} {-5 ; 12} Cos (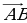 ^ АС ) = ^ АС ) =  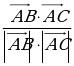 = = 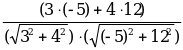 = = 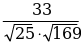 = = 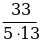 = = 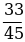 = = 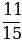 |
8.2. Контрольная работа по теме «Векторы. Метод координат.
Задания
Известны координаты точек А, В, С и D.
Найдите координаты вектора  ,
, 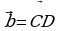 .
.
Найдите их длину (абсолютную величину).
Постройте данные векторы на координатной сетке и постройте вектор их суммы 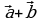 .
.
Найдите координаты вектора суммы данных векторов и его абсолютную величину.
Постройте данные векторы на координатной сетке и постройте вектор разности 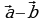 .
.
Найдите координаты вектора разности 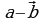 и его абсолютную величину.
и его абсолютную величину.
Найдите координаты вектора 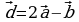 и его абсолютную величину.
и его абсолютную величину.
Найдите скалярное произведение векторов  и
и  .
.
Найдите величину силу 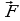 , совершившей работу А по перемещению тела из точки С в точку D. Сила направлена вдоль линии движения.
, совершившей работу А по перемещению тела из точки С в точку D. Сила направлена вдоль линии движения.
БМП с огневой позиции А уничтожила безоткатные орудие В. Появляется танк С. Определить угол поворота башни БМП при переносе огня на танк.
Данные к контрольной работе по вариантам
| Вариант | К о о р д и н а т ы т о ч е к | Величины работы А |
|
|
|
|
|
|
| 1 | A(12; 5) | B(11; 4) | C(1; 1) | D(9; 0) | 24 |
| 2 | A(12; 13) | B(4; 12) | C(7; 0) | D(1; 7) | 16 |
| 3 | A(0; 2) | B(8; 3) | C(5; 3) | D(5; 0) | 45 |
| 4 | A(11; 4) | B(5; 1) | C(3; 8) | D(2; 5) | 15 |
| 5 | A(8; 13) | B(8; 12) | C(5; 9) | D(8; 4) | 11 |
| 6 | A(7; 9) | B(1; 2) | C(2; 7) | D(5; 5) | 14 |
| 7 | A(4; 5) | B(7; 1) | C(1; 6) | D(1; 4) | 16 |
| 8 | A(10; 8) | B(9; 2) | C(4; 2) | D(4; 7) | 25 |
| 9 | A(13; 7) | B(1; 0) | C(1; 3) | D(5; 5) | 8 |
| 10 | A(7; 6) | B(0; 13) | C(8; 9) | D(3; 7) | 16 |
| 11 | A(1; 3) | B(6; 3) | C(7; 9) | D(7; 2) | 42 |
| 12 | A(1; 9) | B(4; 2) | C(7; 4) | D(5; 2) | 28 |
| 13 | A(12; 8) | B(2; 2) | C(5; 8) | D(6; 3) | 15 |
| 14 | A(9; 5) | B(8; 14) | C(8; 1) | D(1; 8) | 49 |
| 15 | A(11; 14) | B(6; 2) | C(1; 9) | D(3; 3) | 68 |
| 16 | A(1; 2) | B(4; 14) | C(1; 9) | D(3; 5) | 17 |
| 17 | A(3; 7) | B(6; 13) | C(5; 5) | D(5; 7) | 26 |
| 18 | A(5; 5) | B(12; 9) | C(5; 1) | D(1; 6) | 32 |
| 19 | A(13; 0) | B(4; 11) | C(0; 9) | D(5; 8) | 35 |
| 20 | A(11; 4) | B(6; 8) | C(2; 2) | D(1; 6) | 20 |
| 21 | A(13; 14) | B(5; 0) | C(1; 2) | D(8; 2) | 28 |
| 22 | A(11; 14) | B(6; 6) | C(4; 8) | D(0; 0) | 26 |
| 23 | A(10; 1) | B(1; 7) | C(7; 5) | D(9; 3) | 11 |
| 24 | A(9; 10) | B(9; 6) | C(6; 2) | D(3; 2) | 30 |
| 25 | A(7; 3) | B(10; 14) | C(1; 2) | D(7; 6) | 28 |
| 26 | A(10; 3) | B(2; 8) | C(0; 9) | D(6; 8) | 12 |
| 27 | A(4; 10) | B(4; 9) | C(7; 1) | D(7; 2) | 13 |
| 28 | A(3; 12) | B(11; 5) | C(1; 6) | D(7; 1) | 78 |
| 29 | A(8; 1) | B(2; 3) | C(1; 4) | D(8; 1) | 38 |
| 30 | A(8; 9) | B(1; 0) | C(6; 3) | D(3; 7) | 40 |
8.3. Задачи военной направленности
БМП с огневой позиции А (-1; -1) уничтожила безоткатное орудие В (4; 4). Появляется танк С (-1; 3). Определить угол поворота БМП при переносе огня на танк.
При занятии обороны командир отделения указал стрелку огневую позицию в точке В (-4; -1) и сектор ведения огня: справа – точка А(1; -2), слева – точка С(3; 0). Определите угол обстрела.
Командир минометной батареи получил задачу на уничтожение противника и его огневых средств в районе, ограниченном точками А(5; 4), В (9; 6), С (6; 7). Какова площадь района обстрела?
«Преодоление искусственных и естественных препятствий»
Задачи, составленные кадетами
1. Снаряд был запущен в точку А(5;6). Во время полета произошло отклонение и снаряд упал в точке В(7;8) и взорвался. Радиус поражения снаряда 5 км. Определить на какое расстояние отклонился снаряд от заданной точки и поразил ли он цель. Составить уравнение окружности, в пределах которой снаряд сохраняет поражающее действие.
Кадет Кузнецов Михаил, 1 взвод 4 роты
2. Из самолета выпрыгнул десант и приземлился в точке В(5:0), затем десантируемая группа выдвинулась на базу противника в точке С(1:0). После уничтожения базы десант на БМП прибыл в указанное место встречи в точку Р(-2;0). Через 20минут из точки Р их подобрал вертолет К-60 «Касатка». Определить путь, пройденный отрядом десанта.
Кадет Пирогов Роман 4 взвод 4 роты
3.Двум разведчикам было приказано из пункта А перейти в пункт К. Первый пошел по маршруту А(3;-3) - В1(0;0) - С1(3;4) - К(-5;3), а второй – по маршруту А(3;-3) - В2(1;-3) - С2(-4;0) - К(-5;3). Выяснить, кто быстрее прибудет в пункт К, если скорость первого равна 6 км/час, скорость второго – 4,5 км/час?
Кадет Горячев Юрий, 2 взвод 3 роты
«Преодоление минного поля"
Задание: от точки М(-7;3) отложите последовательно друг за другом векторы, имеющие координаты: {2;1}, {0;1}, {1;1}, {3;0}, {1;-2}, {0;-2}, {2;-1}, {1;-2}, {3;0}, {3;-2}, {-3;-2}, {-3;1}, {-7;0}, {-1;1}, {-1;2}, {0;2}, {1;2}, {-2;0}. В ответ укажите название фигуры, которая у вас получилась.
«Захват и закрепление на выгодном рубеже»
Используя данное условие как математическую модель задачи, составьте задачу военно-прикладного содержания и решите ее, применяя теорию векторов или метод координат:
Докажите, что средняя линия треугольника параллельна основанию и равна его половине.
Две стороны треугольника равны 17см и 28см, а высота, проведенная к большей из них, равна 15см. Найдите медианы треугольника.
Докажите, что отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
Найдите площадь треугольника АВС, если ВС=4,125 м, угол В равен 440, угол С равен 440.
В равнобедренном треугольнике АВС АВ=ВС=500 м, угол А равен 300. Найдите высоты АЕ и ВD.
Список литературы
Атанасян. Л.С. и др. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений.–М.: Просвещение, 2015.
Богомолов Н.В. Практические занятия по математике.–М.: Высшая школа, 2012.
Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. За страницами учебника математики.–М: Просвещение, 2014.
Гельфанд И.М. и др. Метод координат М.: Наука, 2007.
Глейзер Г.И.: История математики в школе. М.: Просвещение, 1981.
Дорофеев Г.В., Суворова С.Б., Шарыгин И.Ф. и др. Математика. Учебник для 6 класса общеобразовательной школы.–М.: Дрофа, 2015.
Шарыгин И.Ф. Геометрия 7-9 класса, учебник для общеобразовательных учебных заведений.–М.: Дрофа, 2015.
Энциклопедия для детей. Том 11. Математика.-М.: Аванта+, 2003.
20









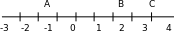




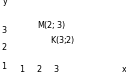

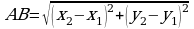
 у
у

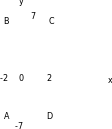


 .7. Консультация второго уровня.
.7. Консультация второго уровня.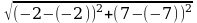 ,
,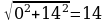 .
.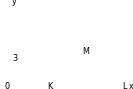



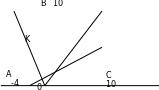
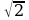 – по теореме Пифагора в
– по теореме Пифагора в 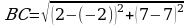 ,
,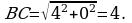
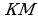 =
= 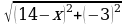 ;
;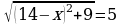 ;
;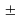
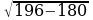 ; х1,2=14
; х1,2=14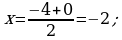
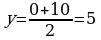 ,
,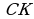 , т.к. С(10;0), то
, т.к. С(10;0), то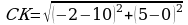 ;
;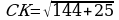 =
=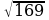 =13,
=13,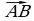 вектор АВ, понимая под этим направленный отрезок АВ, то есть отрезок, у которого точка А является началом, а точка В – концом (рис.9).
вектор АВ, понимая под этим направленный отрезок АВ, то есть отрезок, у которого точка А является началом, а точка В – концом (рис.9). 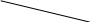 конец вектора
конец вектора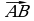 , играют различную роль. Именно в этом состоит главное различие между вектором
, играют различную роль. Именно в этом состоит главное различие между вектором 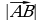 .
.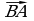 одинаковой длины и противоположного направления.
одинаковой длины и противоположного направления.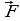 , скорость
, скорость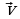 , перемещение
, перемещение 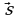 , ускорение
, ускорение  .
.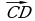 , расположенные на одной прямой, считаются равными, если равны отрезки АВ и CD, то есть равны длины этих векторов, а лучи АВ и CD задают одинаковые направления. Если же векторы
, расположенные на одной прямой, считаются равными, если равны отрезки АВ и CD, то есть равны длины этих векторов, а лучи АВ и CD задают одинаковые направления. Если же векторы  ,
, 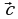 и т.п., помещая в случае необходимости начало соответствующего вектора в любую точку плоскости. Для длины вектора
и т.п., помещая в случае необходимости начало соответствующего вектора в любую точку плоскости. Для длины вектора 





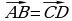
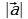 – модуль вектора
– модуль вектора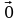 .
.
 асположим векторы
асположим векторы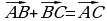


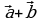
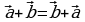
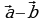 векторов
векторов 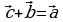 , т.е. это вектор, идущий из конца вектора
, т.е. это вектор, идущий из конца вектора 
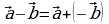
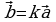 , являющийся произведением вектора
, являющийся произведением вектора 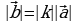 .
.
 онятно, что, если k=0, то получаем нулевой вектор, т.е. точку. Таким образом, длина вектора
онятно, что, если k=0, то получаем нулевой вектор, т.е. точку. Таким образом, длина вектора 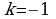 , то получаем вектор –
, то получаем вектор –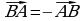 -
- y
y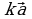 будут {kх; kу}. При сложении (вычитании) векторов их соответствующие координаты складываются (вычитаются), т.е. если векторы
будут {kх; kу}. При сложении (вычитании) векторов их соответствующие координаты складываются (вычитаются), т.е. если векторы 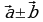 являются
являются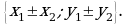


 Теорема: Пусть
Теорема: Пусть 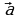 и
и 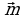 плоскости существует, и притом единственная, пара чисел х и у такая, что
плоскости существует, и притом единственная, пара чисел х и у такая, что 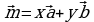 (рис. 17).
(рис. 17).
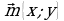
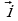 + 2
+ 2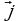 .
.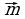
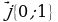
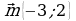
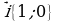
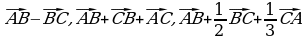 .
.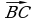 имеет координаты
имеет координаты 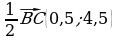 .
. В С
В С 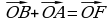
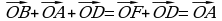
 y Рассмотрим случаи:
y Рассмотрим случаи: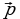 ,
, 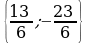
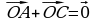 , т.к. эти вектора равны по длине и противоположно направлены.
, т.к. эти вектора равны по длине и противоположно направлены. 
 y тогда
y тогда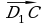 , где D1(х; у)
, где D1(х; у) 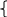

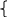 -1-х=1, х=-2,
-1-х=1, х=-2, 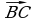 =
=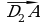 , где D2(х; у)
, где D2(х; у)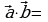
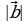 cos φ,
cos φ,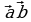 обозначать скалярное произведение ненулевых векторов
обозначать скалярное произведение ненулевых векторов 

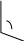
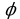

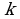 справедливы соотношения:
справедливы соотношения: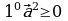 , причем
, причем 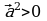 при
при 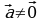
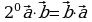 (переместительный закон)
(переместительный закон)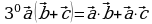 (распределительный закон)
(распределительный закон)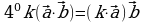 ( сочетательный закон)
( сочетательный закон)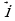 и
и 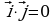 .
.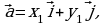
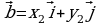
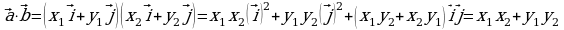 , так как
, так как 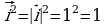 ,
, 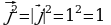 и
и
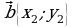
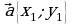
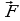 представляет постоянную силу, точка приложения которой перемещается из начала в конец вектора
представляет постоянную силу, точка приложения которой перемещается из начала в конец вектора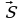 , то работа А этой силы определяется равенством:
, то работа А этой силы определяется равенством: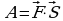
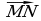 :
: 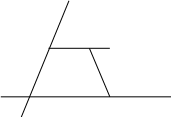
 φ =
φ =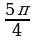 М(ρ; φ)
М(ρ; φ) М(3;
М(3; 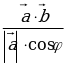 =
= 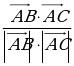 =
= 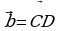 .
.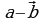 и его абсолютную величину.
и его абсолютную величину.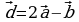 и его абсолютную величину.
и его абсолютную величину.









