Учебно-методическая карта открытого теоретического занятия № 12
по дисциплине «Математика»
Тема " Элементы и множества. Задание множеств. Выполнение операции над множествами. Отношение, свойства отношений "
На уроке использованы педагогические технологии:
Дата 02.11. 2013г. Группа 52-ОК
УЧЕБНО – МЕТОДИЧЕСКАЯ КАРТА ЗАНЯТИЯ № 9
Дисциплина: «Математика»
Раздел: «Основы дискретной математики»
Тема раздела: "Множества и отношения "
Тема занятия: " Элементы и множества. Задание множеств. Выполнение операции над множествами. Отношение, свойства отношений."
Тип урока: урок изучения нового материала
Вид занятия: урок лекция с элементами соревнования
Цели занятия:
образовательные цели:
ввести понятие множества, операций над множествами, рассмотреть способы задания множеств;
способствовать формированию умений применять графический метод при выполнении операций с множествами;
воспитательные цели:
повышать мотивацию студентов путем использования нестандартных задач и игрового изложения материала;
побуждать студентов к само-, взаимоконтролю, вызывать у них потребность в обосновании своих высказываний;
формировать интерес к дисциплине и будущей профессии
развивающие цели:
развить навыки формализации при решении задач с помощью кругов Эйлера;
развивать познавательный интерес к предмету и самостоятельность студентов;
развивать познавательные интересы, логическое мышление, речь и внимание;
способствовать формированию информационной культуры, потребности в приобретении знаний;
побуждать студентов к преодолению трудностей в процессе умственной деятельности;
совершенствовать умения, анализировать и применять полученные ранее знания.
Межпредметные и внутрипредметные связи:
1.обеспечивающие:
«Математика»: последовательности, пределы и ряды. Основные понятия теории графов.
2. обеспечиваемые:
«Математика»: дискретная математика, комбинаторика. Философия. Русский язык. Менеджмент."Математика", дифференцированный зачёт по дисциплине "Математика"
Обеспечение занятия:
1. оборудование:
Проектор, ноутбук;
Математическое лото;
Распечатанные экземпляры технологических карт занятия (для каждого студента) с заданиями;
Презентация к занятию;
Круги Эйлера к заданию №4;
Готовые карточки с домашним заданием;
В качестве раздаточного материала каждый студент получает технологическую карту занятия, в котором указаны задания и рекомендации по их выполнению.
2. литература:
Основные источники:
1. Порошкин А.Г. Элементы теории множеств. Изд.2, – М.: URSS , 2011.
2. Богомолов Н.В. Математика. М.Форум. 20010.
3. Григорьев В.Г. Сабурова Т.Н. “Сборник задач по высшей математике” АКАДЕМИЯ 2009.
Дополнительные источники:
1. ”Теория вероятности и математическая статистика” Спирина М.С.Спирин П.А. Издательский центр “АКАДЕМИЯ” 2009.
2. Виленкин Н.Я. Рассказы о множествах. Изд.4 М.: URSS, 2007. – 152 с.
3.Гохман А.В. и др. Сборник задач по математической логике и алгебре множеств. 1969.
Интернет-ресурсы:
Интернет университет http://www.intuit.ru
Сайт "Все для студента" http://www.twirpx.com
Сайт МЦНМО (Центр непрерывного математического образования)
http://www.mccme.ru
Сайт "Математика, интересная для меня" http://ega-math.narod.ru
Техническая библиотека http://techlibrary.ru
Электронный справочник по математике http://www.pm298.ru
Энциклопедия Кругосвет http://www.krugosvet.ru
ХОД УРОКА
| Структурные элементы урока, методы обучения |
Подструктурные элементы |
Дополнения |
| 1. Организационный момент Метод: собеседование
2. Сообщение темы, плана занятия, постановка целей и задач, объяснение материала Метод: рассказ-объяснение, проблемная лекция, эвристическая беседа, демонстрационный
3.Актуализация знаний Метод: математическая игра
4. Изучение нового материала Метод проблемный метод, метод интерактивного обучения
5.Первичная проверка знаний Метод работа малыми группами, самооценка знаний
6.Закрепление материала Метод решение текстовых задач
7. Итоги и выводы Метод: рассказ-анализ
8. Домашнее задание Метод: объяснение
|
Вступительное слово преподавателя Преподаватель знакомит студентов с ходом проведения урока:
План урока
Актуализация знаний: математическое лото. Актуальность темы и мотивация целей. Изучение нового материала: - определение множества, способы задания множеств, виды множеств; - понятие подмножества; - равенство множеств; - операции над множествами, диаграммы Эйлера – Венна; Первичная проверка знаний. Решение текстовых задач. Обобщение материала. Выдача домашнего задания
Игра «Математическое лото» Методическое обоснование: активизировать внимание студентов и определить общую подготовленность к восприятию новой темы.
Каждый этап изучения новой порции материала закрепляется при решении задач. При изложении нового материала активизируется внимание студентов, устанавливаются внутри дисциплинарные и междисциплинарные связи.
Студенты разбиваются на подгруппы в ходе решения задачи на принадлежность к множеству и занимают места в соответствии со своим решением. Каждому студенту в подгруппе предлагается решить задание №1. Число заданий равно количеству студентов в подгруппе, задания одного уровня сложности, решаются индивидуально каждым студентом. По окончании решения на слайде 2 – 3 решенных преподавателем примера
Решение заданий выполняет каждая подгруппа совместно. Отдельные представители от каждой подгруппы выписывают результаты на доске. На слайде условие заданий, на доске ответы студентов. Сравнивая ответы, делаем вывод. Преподаватель подводит итоги урока, делает выводы, выставляет оценки студентам, активно принимавшим участие в работе группы на занятии.
Студентам предлагается решить задачи по индивидуальным карточкам-заданиям
| 1 мин.
1 мин.
8 мин
3 мин 3 1 - й час 2 мин
15 мин 2 2 - й час 4 мин 2мин. 1 мин.
8 мин
32 мин
15 мин.
24 мин.
2 мин.
1 мин.
|
Организационный момент
Преподаватель приветствует студентов, проверяет их внешний вид и готовность к занятию.
Актуализация знаний: математическое лото.
Эпиграф данного этапа: слова Ф. Бэкона: «Мы столько можем, сколько знаем». (Слайд 1)
(Слайд 2) Студенты играют в математическое лото. На слайде расчерченное поле 3*3 с номерами от 1 до 9. Каждому номеру соответствует задание. Эксперт (из числа студентов) контролирует правильность ответов, делает (если это необходимо), замечания, исправляет неточности, дополняет ответы.
Вопросы к лото:
Какие из перечисленных чисел принадлежат множеству натуральных чисел N: �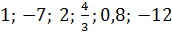 �?
�?
Решите неравенство � �.
�.
Решите уравнение � �
�
Многое, мыслимое как единое.
Какие из перечисленных чисел принадлежат множеству целых чисел Z: � �?
�?
Решите уравнение �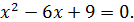 �
�
Решите уравнение �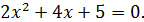 �
�
Какие числа принадлежат отрезку � �
�
Какие числа принадлежат полуинтервалу �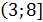 �?
�?
Как видите одна клетка осталась неоткрытой. Давайте откроем ее.
На экране появляется надпись МНОГОЕ, МЫСЛИМОЕ КАК ЕДИНОЕ.
- Как вы думаете, ребята, о чем пойдет речь сегодня на нашем занятии? Студенты высказывают предположения. Преподаватель обобщает сказанное ими: «Оказывается так сказал 140 лет назад немецкий математик и философ Георг Кантор о множествах, которые он использовал, чтобы ответить на вопрос: «Каких чисел больше: натуральных или действительных»?
- А как вы понимаете понятие Множество? (Студенты высказывают предположения).
3) Мотивация целей.
- Хорошо, ребята. Теперь, когда мы выяснили, что речь на сегодняшнем занятии пойдет о множествах, а точнее о большом разделе «ТЕОРИЯ МНОЖЕСТВ», давайте попытаемся ответить на вопрос «Какова же цель нашего занятия? Что мы должны рассмотреть за данную лекцию»? (Студенты высказывают предположения).
- Итак, тема нашего занятия «ТЕРИЯ МНОЖЕСТВ». (Слайд 3)
4) Изучение нового материала
Запишем определение. Множество – это совокупность объектов, рассматриваемых как единое целое.
- Приведите, пожалуйста, примеры множеств.
- В математике часто используют числовые множества: �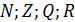 �.
�.
- Предметы, образующие множество, называются его элементами. Множества обычно обозначаются большими латинскими буквами A, B, C, D,…,а элементы множества – малыми латинскими буквами a, b, c, d,…
(Слайд 14)
Существует два способа задания множеств:
Перечислением элементов �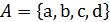 � . При этом мы наглядно видим, из каких элементов состоит множество. Но эта запись неудобна при описании множеств с большим числом элементов или множеств, число элементов которых невозможно перечислить полностью, то есть – бесконечных множеств. Например, невозможно записать все элементы множества чисел, которые делятся на 10.
� . При этом мы наглядно видим, из каких элементов состоит множество. Но эта запись неудобна при описании множеств с большим числом элементов или множеств, число элементов которых невозможно перечислить полностью, то есть – бесконечных множеств. Например, невозможно записать все элементы множества чисел, которые делятся на 10.
Описанием характеристических свойств, которыми обладают все элементы этого множества и не обладает ни один предмет, не являющийся его элементом.
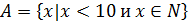
Акцентируется внимание на правильное прочтение такой записи и на то, какие элементы входят в данное множество.
- Как описанием характеристических свойств задать множество четных чисел? Множество нечетных чисел? (Ответы студенты записывают на доске).
- Давайте еще раз потренируемся правильно читать записанные множества.
(Слайд 15).
- Для дальнейшего проведения занятия вы должны разбиться на подгруппы. В мешочках находятся цифры, на столах названия множеств. Вы должны вытянуть одну цифру. Каждая цифра обязательно принадлежит одному из заданных множеств. Ваша задача правильно определить множество и присесть за нужный стол.
Цифры в мешочках заранее подбираются таким образом, чтобы сформировались гетерогенные группы, причем какой – то один стол должен остаться пустым.
После того, как все студенты займут свои новые места, 2 – 3 из них поясняют, почему выбрали именно это множество.
Вы сейчас сидите отдельными группами, маленькими множествами, но в пределах данного занятия вы образуете одно единое большое множество, с которым я сейчас работаю.
(Слайд 17) Самое большое множество, содержащее в себе все множества, рассматриваемые в задаче, называется универсальным. Обозначается U.
Но есть в каждой задаче и самое маленькое множество. Оглядитесь, где оно (стол с табличкой без студентов)? Как оно называется? Как обозначается?
(Слайд 18) Если во множестве нет ни одного элемента, то оно называется пустым множеством� �.
�.
Каждая небольшая группа, на которую вы разбились, является подгруппой большой группы, а, следовательно, является подмножеством множества всей группы. Попробуйте сформулировать определение подмножества.
(Студенты высказывают предположения).
(Слайд 19) Множество A является подмножеством В, если каждый элемент А является также элементом В, и в В есть хотя бы один элемент, не принадлежащий А.
Замечание. Пустое множество �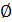 � и само множество всегда являются подмножествами рассматриваемого множества.
� и само множество всегда являются подмножествами рассматриваемого множества.
(Слайд 20) Рассмотрим пример: найдите все элементы множества и запишите его подмножества:
� �
�
� �
�
(Слайд 21) На слайде цитата: «Никогда не беспокой другого тем, что ты можешь сделать сам» Л. Толстой.
Каждому студенту в подгруппе предлагается решить задание №1. Число заданий равно количеству студентов в подгруппе, задания одного уровня сложности, решаются индивидуально каждым студентом.
По окончании решения на слайде 2 – 3 решенных примера.
Задание №1
| На 1 стол. | На 2 стол. |
| Найдите все подмножества множества |
�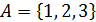 � � �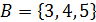 � � � � � �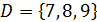 � � �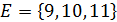 � � �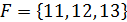 � � | � � � � � � � � � � � � � � � � � � |
| На 3 стол. | На 4 стол. |
| Найдите все элементы множества |
�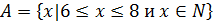 � � � � � �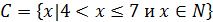 � � �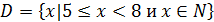 � � � � � � � �
| � � � �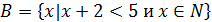 � � �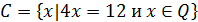 � � � � � � � � �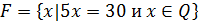 � � |
| На 5 стол. |
| Найдите все элементы множества |
�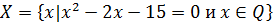 � � � � � � � � � � � �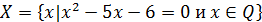 � � � � � |
| Дополнительное задание. Расположите заданные множества в порядке возрастания количества их элементов. |
Множество целых чисел Множество натуральных чисел � � � �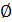 � � |
Перейдем к новому заданию.
(Слайд 23) На слайде цитата: «Взаимная помощь такой же естественный закон, как и взаимная борьба, но для прогрессивного развития вида первая несравненно важнее второго» Карл Кесслер.
Перед вами задание №2. Пример, который в нем находится, выполняет каждая подгруппа совместно.
Задание №2
| На 1 стол. | На 2 стол. |
| Найдите все элементы множества, заданного посредством характеристического уравнения |
� � � | � � � |
| На 3 стол. | На 4 стол. |
| Найдите все элементы множества, заданного посредством характеристического уравнения |
� � � | � � � |
| На 5 стол |
| Найдите все элементы множества, заданного посредством характеристического уравнения |
� � � |
Отдельные представители от каждой подгруппы выписывают результаты на доске. (Слайд 24) На слайде условие заданий, на доске ответы студентов. Сравнивая ответы, делаем вывод. Формулируем определение равенства множеств.
Множества называются равными, если они состоят из одних и тех же элементов.
С помощью нескольких множеств можно строить новые множества или, как говорят, производить операции над множествами. Как вы считаете, какие операции можно проводить над множествами? (Студенты высказывают предположения).
(Слайд 26) Один из величайших математиков петербургской академии Леонард Эйлер (1707–1783) за свою долгую жизнь написал более 850 научных работ. В одной из них появились круги, которые “очень подходят для того, чтобы облегчить наши размышления”. Эти круги и назвали кругами Эйлера. С помощью этих кругов удобно геометрически иллюстрировать операции над множествами.
(Слайд 27 - 34).
Объединение множеств
Объединением А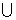 В множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.
В множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.
Символическая запись этого определения: А 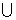 В={х | х
В={х | х А или х
А или х В}.
В}.
Поясним определение объединения множеств с помощью диаграммы Эйлера-Венна:
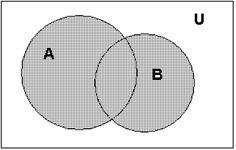
На диаграмме объединение множеств А и В выделено штриховкой.
Если множество А определяется характеристическим свойством Р (х), а множество В - характеристическим свойством Q(х), то А 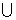 В состоит из всех элементов, обладающих, по крайней мере, одним из этих свойств.
В состоит из всех элементов, обладающих, по крайней мере, одним из этих свойств.
Примеры объединений двух множеств:
1) Пусть А={2; 5; 7}, В={3; 5; 6}. Тогда А 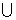 В ={2; 3; 5; 6; 7}.
В ={2; 3; 5; 6; 7}.
Пересечение множеств
Пересечением А ∩ В множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из множеств А и В.
Символическая запись этого определения: А ∩ В={х | х А и х
А и х  В}.
В}.
Поясним определение пересечения множеств с помощью диаграммы Эйлера-Венна:
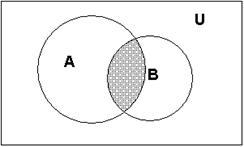
А ∩ В
На диаграмме пересечение множеств А и В выделено штриховкой.
Примеры пересечений двух множеств:
1) Пусть А={2; 5; 7; 8}, В={3; 5; 6; 7} .Тогда А ∩ В={5; 7}.
2) Пусть А- множество всех прямоугольников, В-множество всех ромбов. Тогда А ∩ В -множество фигур, одновременно являющихся и прямоугольниками, и ромбами, т.е. множество всех квадратов.
Разность множеств
Разностью А\В множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В, т.е.
А\В={х | х  А и х
А и х В},
В},
что можно пояснить на диаграмме Эйлера-Венна следующим образом:
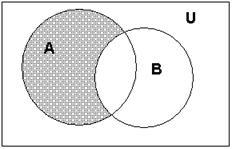
На диаграмме разность А\В выделена штриховкой.
Примеры разностей множеств:
1. Пусть А={1; 2; 5; 7}, В={1; 3; 5; 6}. Тогда А\В ={2;7}, а В\А={3; 6}.
Дополнение множества
Пусть множество А и В таковы, что А В. Тогда дополнением множества А до множества В называется разность В\А. В этом случае применяется обозначение СBА=В\А. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=СUА=U\А и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей:
В. Тогда дополнением множества А до множества В называется разность В\А. В этом случае применяется обозначение СBА=В\А. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=СUА=U\А и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей:  СА={x | x
СА={x | x  A}.
A}.
На диаграммах Эйлера-Венна можно так пояснить определения СВА и СА:
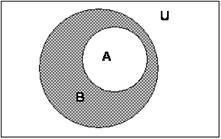
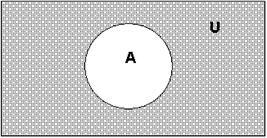
(Слайд 35, 36) Рассмотрим пример:
Найдите � � если �
� если � �, �
�, �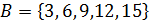 �.
�.
Установите соответствие
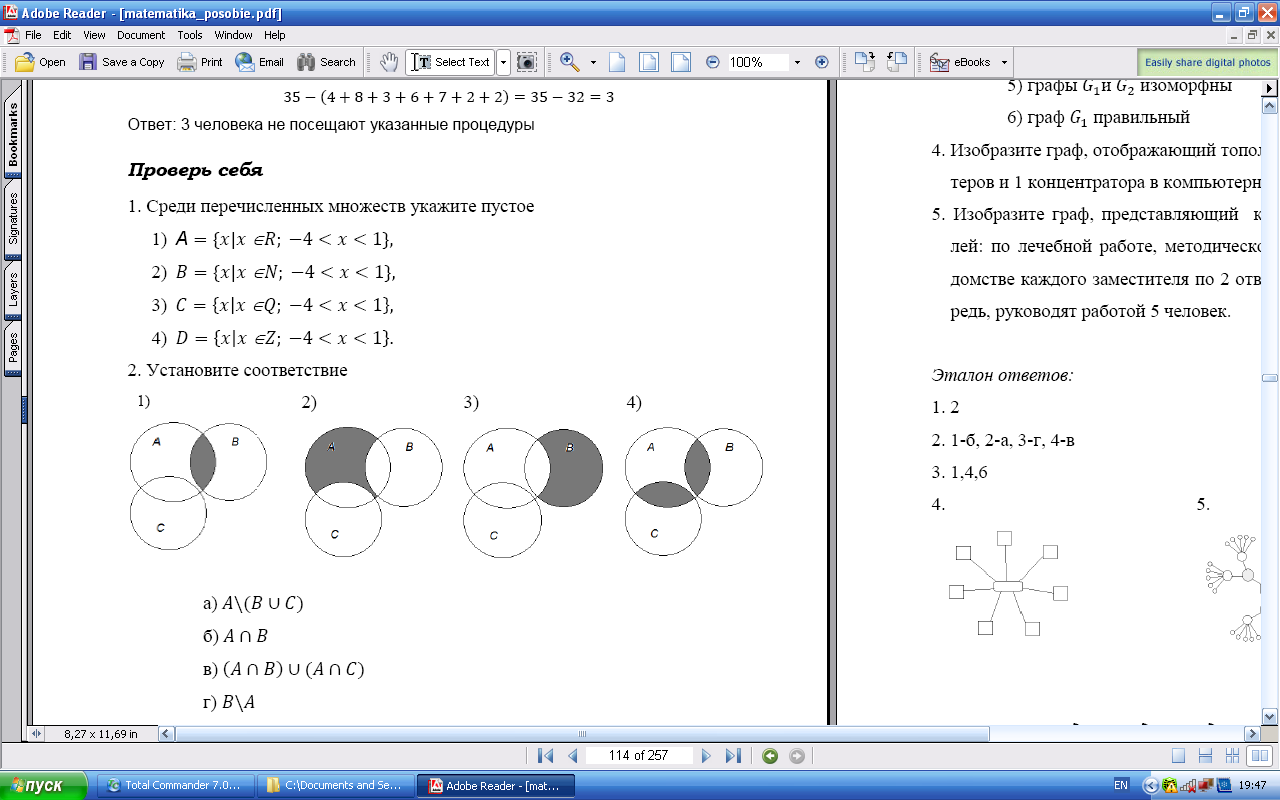
� � b) �
� b) � � c) �
� c) �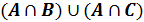 � d) B\A
� d) B\A
Ответ: 1 – b, 2 – а, 3 – d, 4 – с.
Задание №3 (выполняет каждая подгруппа совместно).
Заполните таблицу.
| Множества | 
| 
| 
| 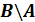
|
|
| 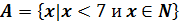 
|
|
|
|
| 1 стол |
| 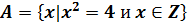 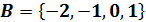
|
|
|
|
| 2 стол |
|  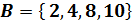
|
|
|
|
| 3 стол |
|  
|
|
|
|
| 4 стол |
|  
|
|
|
|
| 5 стол |
Задание №4 (выполняет каждая подгруппа совместно).
Заштрихуйте ту часть диаграммы, которая соответствует следующему множеству:
| Множества |
|
| 
| 
| 1 стол |
| 
| 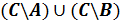
| 2 стол |
| 
| 
| 3 стол |
| 
| 
| 4 стол |
| 
| 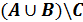
| 5 стол |
Представители каждой группы отмечают результат на доске.
Первичная проверка знаний.
Подведем промежуточный итог (в зависимости от оставшегося времени проводится или фронтальный опрос или игра «Морской бой»).
Вопросы для фронтального опроса берутся из игры «Морской бой».
Слайд 37
Лист с фигурой для 1половины группы
Лист с фигурой для второй половины группы.
Вопросы:
А1: Сколько подмножеств у множества � �
�
A2: Встретились 6 студентов. Каждый, здороваясь, пожал каждому руку. Сколько всего рукопожатий было сделано?
A3: Каким способом задано множество �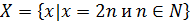 �?
�?
B1: Какая операция изображена на рисунке 
C4: Чему равно � �, если �
�, если � �, �
�, �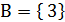 �
�
D4: Каким способом задано множество � �.
�.
E4: Какая операция изображена на рисунке 
E3: Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было10 рукопожатий?
Решение текстовых задач
- Рассмотрим другую сторону применения теории множеств – решение текстовых задач.
Разминка: (Слайд 20, одинаковые задачи для всех групп на скорость выполнения).
Задача1. Иван не Иванов, Петр не Петров, Сергей не Сергеев. Сергей живет в одном доме с Петровым. Кто есть кто? (ответ: Сергей Иванов, Петр Сергеев, Иван Петров).
Задача2. В банкетном зале работает 5 официантов. Нужно составить график дежурств по 2 человека на смену, причем каждый официант должен отдежурить с каждым из остальных. На сколько смен будет составлен график? (ответ: 10, обращаем внимание, что эту задачу можно решить как при помощи теории множеств, так и при помощи комбинаторики, используя размещения без повторений).
Дополнительные задания. А теперь перейдем к более сложным задачам.
Задача3. Из 100 первокурсников колледжа посещают кружок «Технология обслуживания в общественном питании» 30 человек, кружок «Карвинг» – 28, кружок «Организация обслуживания» – 42. Кружки «Технология обслуживания в общественном питании» и «Карвинг» посещают 8 человек, кружки «Карвинг» и «Организация обслуживания» – 10, «Технология обслуживания в общественном питании» и «Организация обслуживания»– 5, а все три – 3 человека. Сколько студентов не посещают ни один кружок?
Решение: (объясняет преподаватель)
Решим задачу с помощью кругов Эйлера. Пусть
| 
| Множество студентов, посещающих кружок по педиатрии.
|
| 
| Множество студентов, посещающих кружок по хирургии. |
| 
| Множество студентов, посещающих кружок по основам сестринского дела. |
Тогда
U=100
П=30
Х=28
С=42
�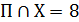 �
�
�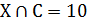 �
�
� �
�
� �
�
Ни одного кружка - ?
Отметим исходные данные на диаграмме Эйлера – Венна.

Отметим неизвестную величину буквой y. Составим уравнение
Y+20+13+30+5+7+2+3=100
Y=20
Ответ: 20 студентов не посещают ни один кружок.
Задача 4: В кафе работают 36 человек. Из них на стажировке в Германии побывали 18 человек, во Франции – 14 человек, в Италии – 10 человек. Кроме того, известно, что все три страны посетили 2 человека, Германию и Францию – 8, Германию и Италию – 5, Францию и Италию – 3. Сколько сотрудников не прошли стажировку за рубежом?
Обобщение материала: подводится итог работы и выставляются оценки.
Домашнее задание.
В группе учатся 40 студентов. Из них по русскому языку имеют «пятерки» 19 человек, по математике – 17 человек и по информатике – 22 человека. Только по одному предмету имеют «пятерки»: по русскому языку – 4 человека, по математике – 4 человека, по информатике – 11 человек. Семь студентов имеют «пятерки» и по математике и по информатике, а 5 студентов – «пятерки» по всем предметам. Сколько человек учится без «пяте-рок»? Сколько человек имеют «пятерки» по двум из трех предметов?
Из пункта А в пункт В выехали пять машин одной марки разного цвета: белая, черная, красная, синяя, зеленая. Черная едет впереди синей, зеленая — впереди белой, но позади синей, красная — впереди черной. Каков порядок их движения?

Запишите множество, изображенное с помощью кругов Эйлера на рисунке:





























