Уравнения и неравенства с параметрами как способ формирования исследовательских навыков учащихся в курсе алгебры 7-9 класса
И. М. Шумская
ГБОУ ЛНР «Кировская многопрофильная гимназия»,
г. Кировск
[email protected]
Аннотация. В последние годы задачи с параметрами (и прежде всего уравнения и неравенства с одним параметром) регулярно встречаются в вариантах ГИА, олимпиадах, ЕГЭ. И здесь далеко не все школьники приступают к решению этих заданий, и еще меньшее число – выполняют решение верно. Таким образом, очевидна необходимость отработки в школьном курсе математики приемов решения различных задач с параметрами.
Ключевые слова: исследование, неравенства, параметры, решение задач, школьный курс.
Актуальность проблемы. Решение уравнений и неравенств, содержащих параметр, является, пожалуй, одним из самых трудных разделов элементарной математики. Это связано с тем, что в школе стараются развить умения и навыки решения определенного набора стандартных задач, связанных часто с техникой алгебраических преобразований. Задачи с параметром относятся к другому типу. Для их решения обычно требуются гибкость мышления, логика в рассуждениях, умение хорошо и полно анализировать ситуацию. Опыт показывает, что учащиеся, владеющие методами решения задач с параметром, успешно справляются и с другими задачами.
Цель статьи. Привести примеры решения задач с параметрами, показав собственный опыт формирования у учащихся умений, навыков и математической компетентности при решении задач с параметрами.
Впервые знакомиться с параметрами полезно в 7-м классе при изучении линейных уравнений, чтобы ученики привыкли к понятию «параметр» и не испытывали затруднений при изучении этой темы в старших классах.
Прежде чем ввести понятие «параметр» ученикам необходимо напомнить роль буквы в алгебре и предложить задания в которых надо выразить одну переменную через другую.
Задание: Выразите х через другие переменные:



Пример 1. Решите уравнение х + 2 = а + 7 относительно х.
Переменную, которую надо найти, будем называть неизвестной, а переменную, через которую будем выражать искомую неизвестную, назовем параметром.
Решить уравнение с параметром – это значит для каждого значения параметра найти значение неизвестной переменной, удовлетворяющее этому уравнению.
х + 2 = а + 7; х = 5 + а
Значение х находится по формуле х = 5 + а, подставляя в нее задаваемые значения параметра а. Заметим, что значения параметра а задаем произвольно.
В нашем примере: при а = 3 х = 8; при а = 0 х = 5; при а = –4 х = 1.
Ответ запишем так: при любом значении параметра а х = 5 + а.
Параллельно решаем задачу, обратную данной.
Пример 2. При каком значении параметра а х = 2,5 является корнем уравнения х + 2 = а + 7?
Решение.
Т.к. х = 2,5 корень уравнения х + 2 = а + 7, то при подстановке х = 2,5 в уравнение получим верное равенство: 2,5 + 2 = а + 7
а = – 2,5
Ответ: при а = – 2,5.
В 7 классе начинаем обращать внимание учеников на запись ответа.
1) при а …. х ….
2) если а …. , то х ….
Когда начинать решать такие уравнения? В зависимости от уровня класса, на уроках в течение всего года.
Решение квадратных и дробно-рациональных уравнений, содержащих параметры – один из труднейших разделов школьной математики. Квадратные и дробно-рациональные уравнения с параметрами – это тема, на которой проверяется подлинное понимание учащимися изученного материала.
Что должны знать восьмиклассники?
Если D 0, то уравнение  имеет два корня
имеет два корня
 и
и  .
.
Если D = 0, то уравнение  имеет один корень
имеет один корень  .
.
Если D не имеет корней
Пример 3. При каких значениях параметра b уравнение 
а) имеет корни; б) не имеет корней?
Решение.  ; D =
; D =  ;
;

 , следовательно
, следовательно  Если
Если  , то уравнение корни имеет.
, то уравнение корни имеет.
б) 
 , – при любых значениях b, кроме нуля. Если b Î (– ¥; 0) È (0; + ¥), то исходное уравнение корней не имеет.
, – при любых значениях b, кроме нуля. Если b Î (– ¥; 0) È (0; + ¥), то исходное уравнение корней не имеет.
Уже в 8 классе можно решать квадратные уравнения, содержащие параметр, с ограничением на корни.
К этой группе задач примыкают задачи, содержащие параметр, решаемые с использованием теоремы Виета.
Пример 4. При каких значениях параметра b уравнение
 имеет:
имеет:
а) два положительных корня; б) два отрицательных корня; в) единственный корень?
Решение.
Если b ¹ 1, то 
а) согласно теореме Виета  , b Î (– ¥; – 1) È ( – 1; + ¥)
, b Î (– ¥; – 1) È ( – 1; + ¥)
б) , решений нет
, решений нет
в) если b = 1, то –2х + 2 = 0; х = 1; b ¹ 1;  .
.
Ответ: а) b Î (– ¥; – 1) È ( – 1; + ¥); б) таких b не существует; в) х = 1.
В 9 классе рассматриваем задания, которые связаны с решением квадратичных неравенств, уравнений на расположение корней квадратного уравнения, графическим методом решения уравнений с параметрами, в том числе, уравнений с модулями.
Для решения квадратных неравенств с параметрами следует добиться осмысленного усвоения алгоритма решения квадратичных неравенств вида ах2 + bх + с 0; ах2 + bх + с 2 + bх + с ≥ 0; ах2 + bх + с ≤ 0. Наглядной «помощницей» может быть таблица. 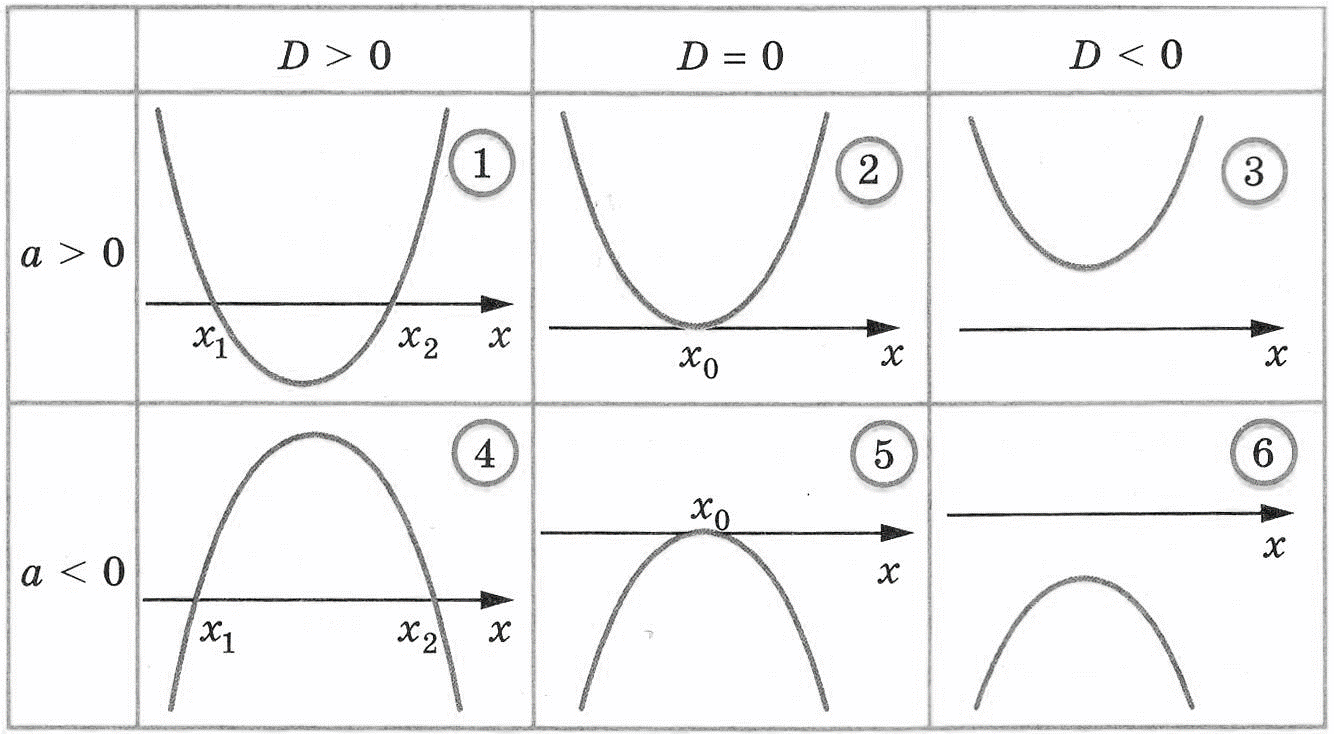
Пример 5. Найдите число решений уравнения  в зависимости от параметра а.
в зависимости от параметра а.
Решение.
Построим график функции  .
.
Выделим полный квадрат 
Уравнение  имеет столько решений, сколько раз прямая
имеет столько решений, сколько раз прямая  пересекает график функции
пересекает график функции  . На рисунке видно:
. На рисунке видно:
1) если  , то графики не имеют общих точек, т.е. нет решения;
, то графики не имеют общих точек, т.е. нет решения;
2) если  , то графики имеют две общие точки, т.е. два решения;
, то графики имеют две общие точки, т.е. два решения;
3) если  , то графики пересекаются в четырех точках – что дает четыре решения;
, то графики пересекаются в четырех точках – что дает четыре решения;
4) если  , то графики имеют три общие точки , т.е. три решения;
, то графики имеют три общие точки , т.е. три решения;
5) если  , то графики имеют две общие точки , т.е. два решения.
, то графики имеют две общие точки , т.е. два решения.
Использование в школьном курсе задач с параметрами способствует выполнению основной задачи математического образования: научить учащихся учиться, причем не только в школе, а и всю жизнь, сформировать математические компетентности, которые являются основой интеллектуальных компетентностей личности, социально-трудовые, коммуникативные и информационные компетентности. Помогает достигнуть цели школьного образования, а именно, дать возможность учиться для формирования компетентностей личности.
Список использованных источников
1. Горнштейн П.Н., Полонский В.Б., Якир М.С. Задачи с параметрами. – М.: Илекса, 1998. – 336 с.
2. Кожухов С. К. Уравнения и неравенства с параметрами. Учебное пособие. – Орел, 2013. – 72 с.
3. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 8. – Харьков: Гимназия, 2008. – 368 с.
9. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 9. - Харьков: Гимназия, 2009. – 382 с.
2








 имеет два корня
имеет два корня  и
и  .
. .
.
 ;
;
 , следовательно
, следовательно  Если
Если  , то уравнение корни имеет.
, то уравнение корни имеет.
 , – при любых значениях b, кроме нуля. Если b Î (– ¥; 0) È (0; + ¥), то исходное уравнение корней не имеет.
, – при любых значениях b, кроме нуля. Если b Î (– ¥; 0) È (0; + ¥), то исходное уравнение корней не имеет. имеет:
имеет: 
 , b Î (– ¥; – 1) È ( – 1; + ¥)
, b Î (– ¥; – 1) È ( – 1; + ¥) , решений нет
, решений нет .
.
 в зависимости от параметра а.
в зависимости от параметра а.









